横观各向同性岩石亚临界裂纹扩展实验研究

王思青，李江腾，王聪聪



横观各向同性岩石亚临界裂纹扩展实验研究

王思青，李江腾，王聪聪

(中南大学资源与安全工程学院，湖南长沙，410083)

在MTS Insight电子拉力试验机上采用常位移松弛法，对具横观各向同性的板岩开展亚临界裂纹扩展试验研究，获得应力强度因子I与裂纹扩展速率的关系及I型断裂韧度IC，揭示不同节理倾角下裂纹亚临界扩展规律。研究结果表明：各个节理倾角下的lgI−lg具有很好的线性规律；当节理倾角为0°~45°时，回归参数随倾角的增大而增大，回归参数随倾角的增大而减小；当节理倾角为45°~90°时，回归参数随倾角的增大而减小，回归参数随倾角的增大而增大，亚临界裂纹扩展参数和分别与回归参数和变化规律相同；断裂韧度IC以及松弛最大荷载max均符合“U”型抛物线分布，当节理倾角为0°~45°时，两者随倾角的增加而减小，当节理倾角为45°~90°时，两者随倾角的增加而增大，同时，两者均在节理倾角为0°时取得最大值，在节理倾角为45°时取得最小值。

MTS Insight电子拉力试验机；横观各向同性；常位移松弛法；亚临界裂纹扩展；断裂韧度

岩体是结构面和完整岩石组成的地质结构体，与一般介质的重大差别在于它是由众多结构面纵、横切割而具有一定结构的多裂隙体。任何岩体工程的失稳破坏都是岩体中裂纹产生、扩展及贯通的结果，其主要经过裂隙孕育阶段—裂纹的稳定、准静态扩展阶段—裂纹快速发展岩石破坏阶段。从裂纹稳定扩展阶段过渡到岩石破坏阶段，断裂韧度存在1个临界值即IC。根据断裂力学原理和应力腐蚀理论，当应力强度因子I小于IC时，裂纹扩展则以应力腐蚀亚临界裂纹扩展速度稳定地进行。国内外多采用双扭试验方法研究材料亚临界裂纹扩展规律以及断裂韧度。该方法最先用于测试玻璃、陶瓷和钢材的断裂特性，目前也广泛应用于岩石材料亚临界裂纹扩展规律以及断裂韧度的研究，但国内外大部分双扭实验均视岩石为各向同性。其中，国内针对花岗岩、大理岩以及混合岩等各类岩石，基于各向同性理论研究其亚临界裂纹扩展规律[1−5]以及考虑水作用下的亚临界裂纹扩展规 律[6−7]；国外运用双扭实验研究亚临界裂纹扩展的理论，实验研究与模拟研究相结合[8−12]，且将该方法应用于混凝土路面的裂纹扩展[13]。岩石内部存在大量的微结构面，这使岩石具有明显的非均质性、各向异性的特性，显然，对岩石的各向同性假定有很大的局限性。NARA 等[14−15]基于正交各向异性的理论对3个正交方向岩石进行了双扭实验研究。为进一步丰富和发展岩石亚临界裂纹扩展理论，本文作者在横观各向同性的理论基础上[16−18]，对板岩开展了双扭实验，以揭示这一具横观各向同性的岩石亚临界裂纹扩展规律。

1 横观各向同性理论

岩体因受内部联结力较弱的层理、片理和节理、断层等切割而具有明显的不连续性，因此，其本身各个方向力学特性均不同，即具极端各向异性，但在研究过程中常进行一定假设并加以简化分析，目前主要集中在岩体的正交各向异性、岩体的横观各向同性以及岩体的各向同性的研究。对于层理状岩石，其变形具有明显的各向异性，通常作为横观各向同性体来研究其力学行为。

广义Hooke定律基于连续、均匀、无初应力、变形微小的基本假设，根据连续介质力学理论可推导出表示线弹性固体中任意1点的应力－应变关系，可用下式描述：

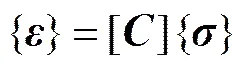
或(1)

式中：[]为柔度矩阵；C为个弹性柔度常数。根据弹性应变能原理，柔度矩阵[]可简化为含有21个独立参数的对称矩阵。对于正交各向异性岩石，其本构关系中的[]最终可简化为仅含9个独立参数。横观各向同性是正交各向异性的1个特殊情况，其平行于某一个平面的任意方向上均具有相同的弹性参数，而其垂直的方向则具有不同的弹性参数，即式(1)最终可简化为

式中：1为各向同性平面(平面)内所有方向的弹性模量(1=E=E)；2为垂直于各向同性平面弹性模量(E)；为各向同性平面内的泊松比；为各向同性平面法向应力引起的各向同性平面方向的应变与其法线方向应变之比；1为各向同性平面的剪切模量，且；2为垂直于各向同性平面上的剪切模量。基本模型见图1。

据文献[19]，当各向同性面绕轴旋转后，其坐标系变为’，’和’，其柔度矩阵[]’的弹性柔度常数C’可以由矩阵[]中的C通过张量转换得到，结合柔度矩阵中常数与岩石弹性常数的关系，可获得如下关系式：

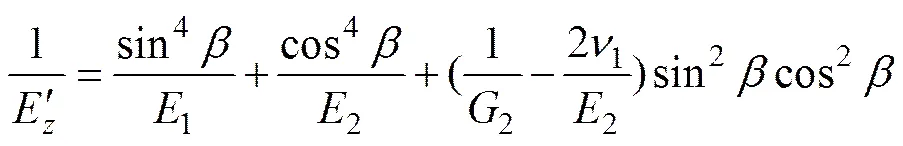
(3)

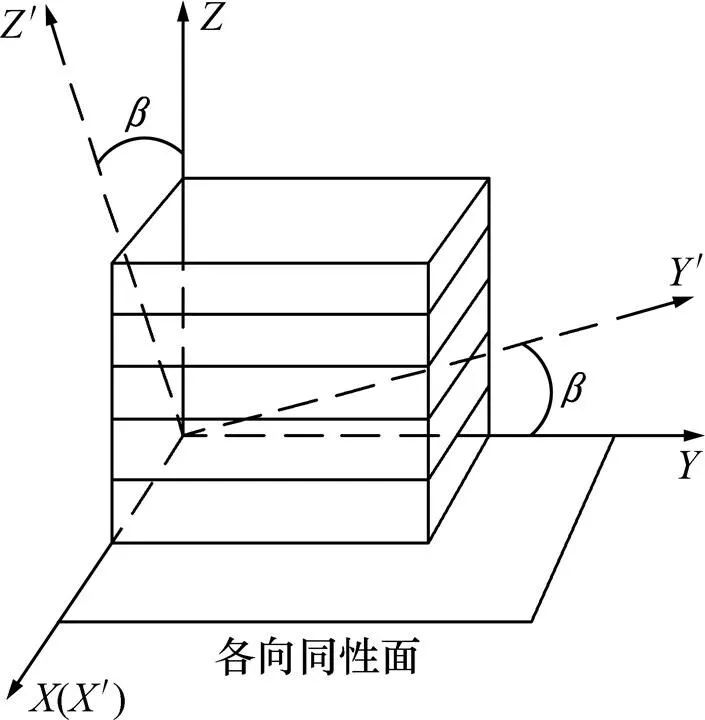
图1 横观各向同性材料示意图

单轴压缩条件下的弹性参数可通过单轴压缩试验获得。具有一定角度的层理切割的岩石，其单轴压缩实验试件如图2所示。令其轴向弹性模量为，泊松比为和，剪切模量为，和，对比图1与图2，可知层理面与水平面夹角为的各项弹性参数均满足关系式(3)。通过简单变化可推出：

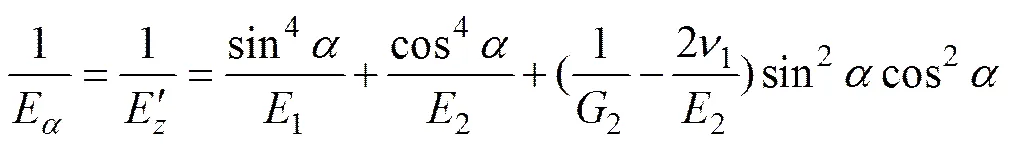
由式(4)可获得单轴试验下的弹性模量与泊松比、剪切模量及岩石节理倾角的关系式。

图2 单轴压缩实验试件分析图

Fig. 2 Aanalysis diagram of uniaxial compression test specimen

2 亚临界裂纹扩展实验

2.1 实验原理

双扭试件试验如图3 所示，试件为1个矩形薄板，在板的下表面沿长边方向对称线开1个中槽，使裂纹沿中槽扩展。试件可以看作由2个弹性扭转杆组成，依据材料力学中关于实心非圆截面杆件的研究可得其扭矩应变，表示为[20]

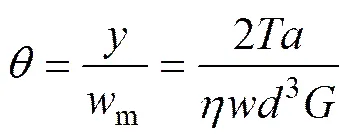
式中：为加载点的位移；m为扭臂长度；为扭矩，；为作用于扭杆上的荷载；为岩石的剪切模量；为裂纹长度；为试件厚度；/2为扭杆宽度；为与/有关的参数(本文实验取/=10，故=0.312)。

(a) 试件形状；(b) 横向截面；(c) 纵向截面

图3 双扭试件示意图

Fig. 3 Schematic diagrams of double torsion specimen

根据柔度定义并结合式(5)有

裂纹扩展的应变能释放率与试件的柔度有如下关系[21]：

(7)

式中：为应变能；为裂纹面积；n为切口的厚度。应力强度因子I与应变能释放率之间的关系为

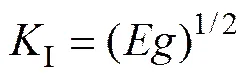
将式(6)中对求导，并将结果代入式(7)，结合式(8)可得到应力强度因子关系式：

(9)

当载荷达到临界值C时，裂纹快速扩展。此时，I也达到临界值即断裂韧度IC：

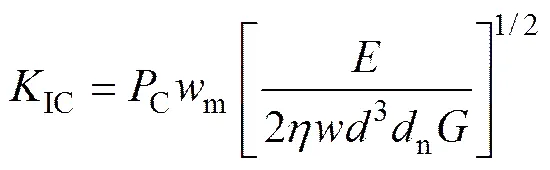
在恒定位移条件下，对式(6)两边同时对时间求导，得到岩石亚临界裂纹扩展速度为

(11)

由式(9)和(11)可知应力强度因子与荷载、试件尺寸(长、宽、高)、弹性模量、剪切模量等因素有关，不依赖裂纹的长度。对于裂纹扩展速度，在给定位移状态下，若试件尺寸已知，则其与此荷载作用下的荷载松弛率有关。双扭方法在确定应力强度因子及亚临界裂纹扩展速率时不需要知道裂纹长度，因而避免了裂纹扩展长度测量与跟踪等难题。

2.2 试样制备

用岩石切割机将板岩锯成薄片，再在金刚砂磨石机上磨光，沿中央轴线用金刚石锯片锯制1条通槽，槽宽为2 mm，槽深约为/3。在试件加载方向导向槽位置，切割1条“V”型切口，深约1 mm，使得在加载过程中裂纹从切口开始，沿导向槽延伸。加工时试样上、下表面平整，不平行度误差在0.025 以内。将试件分成6组，每组试件节理倾角(即节理与双扭试件短边的夹角)依次为0°，30°，45°，70°，80°和90°，分别对应组号为1号、2号、3号、4号、5号和6号。由横观各向同性可知，对于90°试样，其满足G=G的关系[22]。同样，当节理倾角为0°时，G=G亦适用。通过单轴压缩实验并依据式(3)，最终获得6组试件的尺寸(长、宽、高)及基本力学参数，如表1所示。

2.3 实验装置

实验在中南大学测试中心MTS Insight电子拉力试验机上进行。位移、荷载和时间同时采用计算机控制与采集系统自动记录。对比INSTRON 1342 材料伺服机，本文采用的电力控制较液压控制更准确，且其量程为1 kN，适用于受力比较小的双扭实验。实验装置见图4。

2.4 测试方法

考虑到板岩层理发育程度较高，为获得合理的IC，I和，实验中减小荷载的加载速度。对试件以恒定位移速率(0.02 mm/min)进行预裂，记录荷载随时间的变化。当荷载基本不随时间上升时，停止加载，预裂完成。此后，将预裂好的试件采用常位移松弛法进行亚临界裂纹扩展速率测试。实验采用位移控制方法，以0.1 mm/min 的速度对试件加载，当荷载达到其预裂荷载的95%时，控制试件上的位移，使其保持恒定，并对试件进行松弛实验，整个松弛实验过程需要20~40 min。最后，测试IC，以10 mm/min 的恒位移速率对试件加载直至试件断裂，测得其破坏荷载。

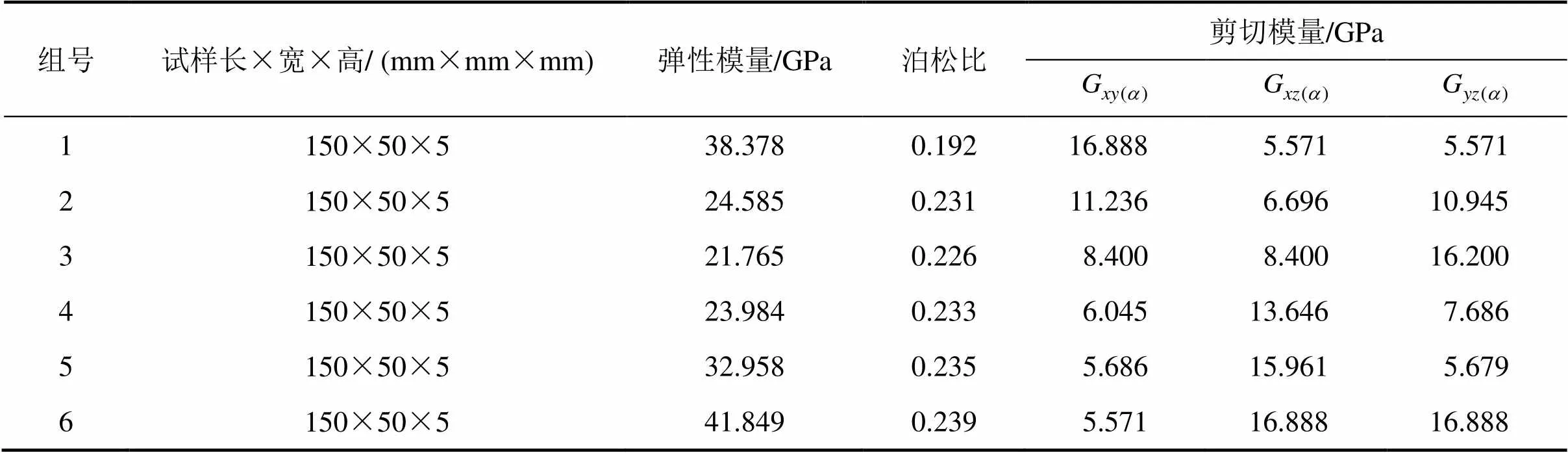
表1 试样尺寸与基本力学参数

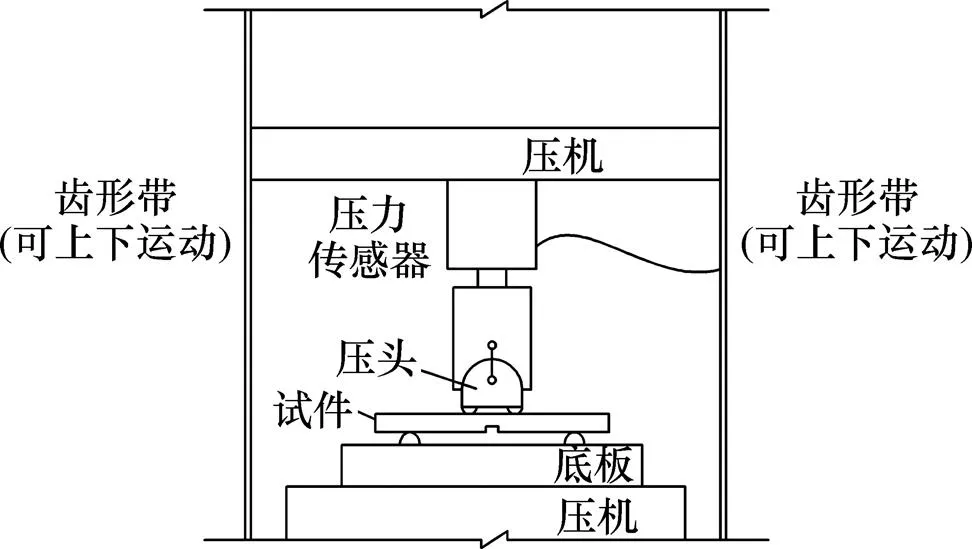
图4 MTS Insight电子拉力试验机示意图

3 结果与分析

3.1 常位移松弛−曲线测试

用常位移松弛法测试板岩试件−曲线，图5所示为6组不同层理角下试样的载荷−松弛曲线。根据式(9)~(11)分别计算得到I以及IC和，其中剪切模量根据要求均取。

试样的松弛最大荷载与节理倾角关系见图6，对其进行拟合，可得到理想的光滑抛物线曲线。从图6可见：当节理倾角为0°即节理与短边平行时，松弛最大荷载max取得最大值，倾角为45°时其取得最小值；当节理倾角小于45°时，max随角度的增大而减小，而当节理倾角大于45°时，max随角度的增大而增大。

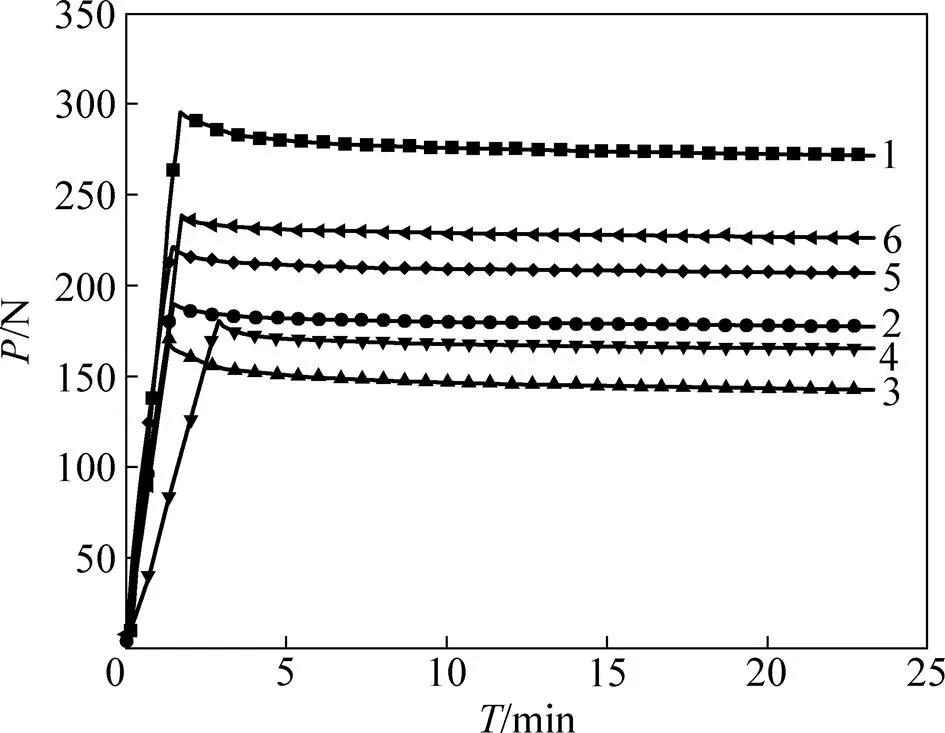
试样：1—1号；2—2号；3—3号；4—4号；5—5号；6—6号。

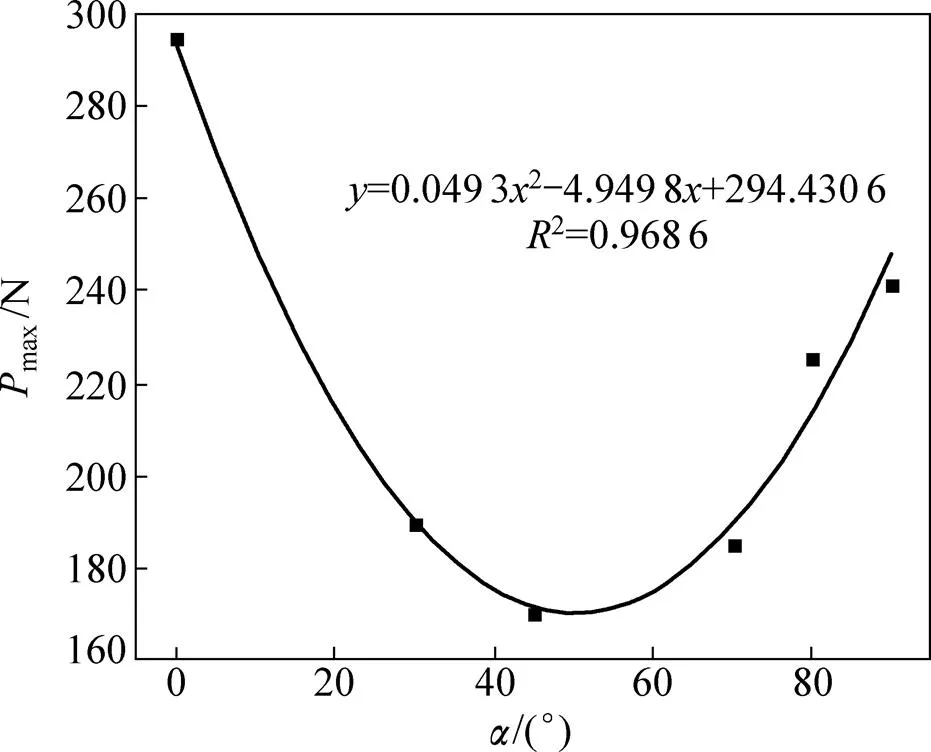
图6 松弛最大荷载与节理倾角的关系

3.2I−关系

由Charles 理论可知，裂纹扩展速率与应力强度I因子满足幂函数关系：

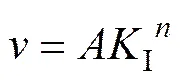
(13)

式中：，，和均为常数；=10；=；和为回归参数；和为亚临界裂纹扩展参数。

根据常位移松弛试验的−曲线，通过式(9)和式(11)可以得到各试样的裂纹扩展速度与裂纹尖端应力强度因子。6组代表试样在双对数坐标系中I−散点图见图7。

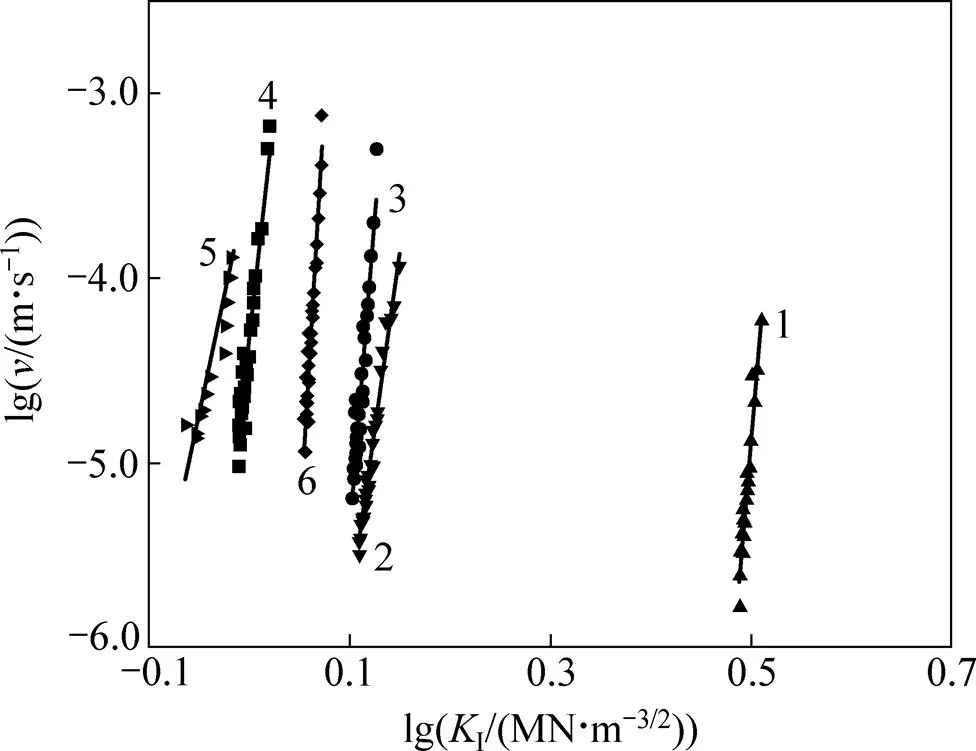
试样：1—1号；2—2号；3—3号；4—4号；5—5号；6—6号。

根据式(13)对I−曲线进行线性回归，获得试件的回归参数和及相关系数2，见表2；据式(12)获得亚临界裂纹扩展参数，见表3；据式(10)计算出断裂韧度，见表4。

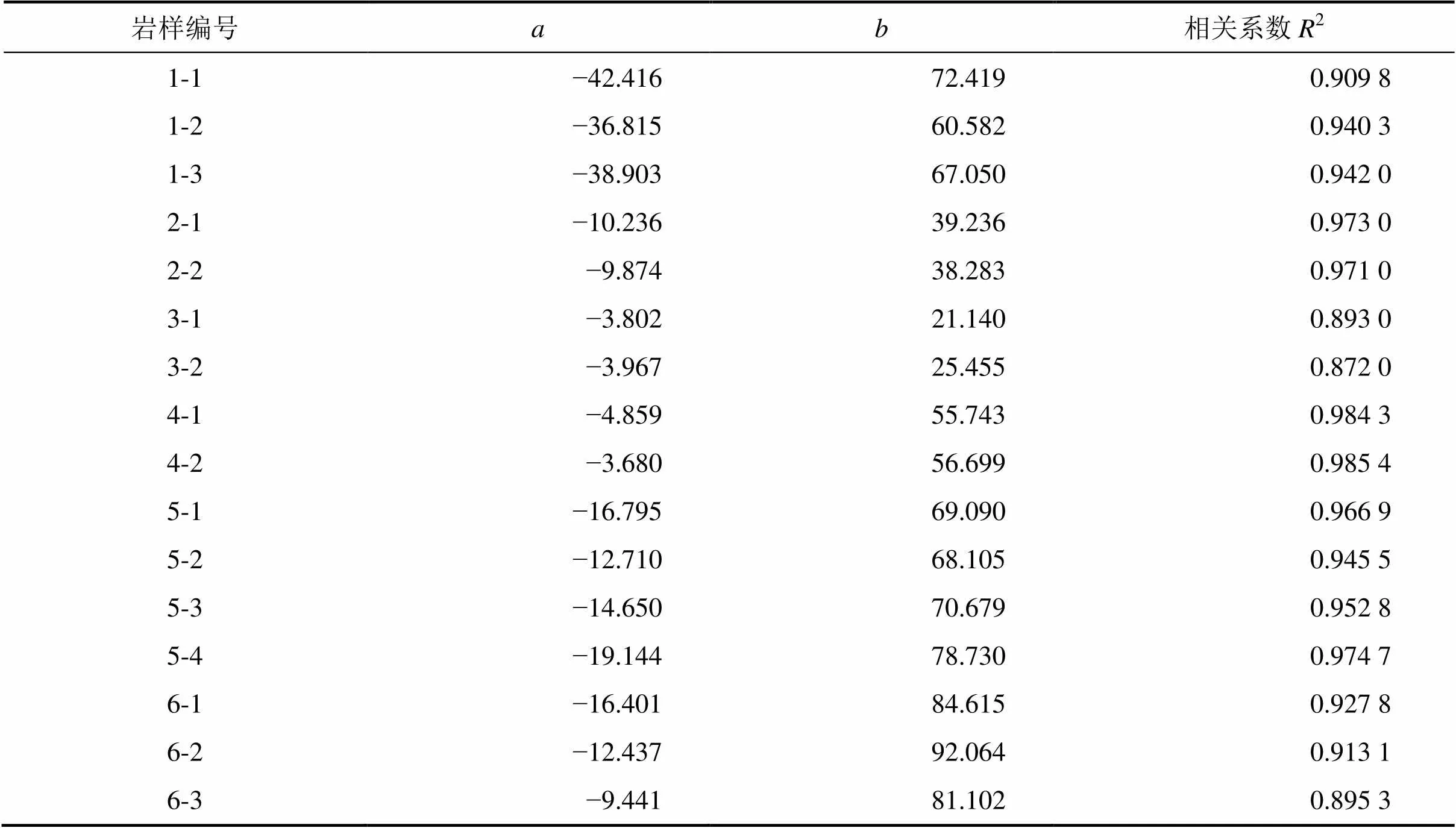
表2 亚临界裂纹扩展回归参数

表3 亚临界裂纹扩展参数

表4 断裂韧度KIC

3.3 亚临界裂纹扩展各参数与节理倾角

线性回归获得的回归参数和与节理倾角的关系见图8。从图8可见：在节理倾角为0°~45°时，回归参数随倾角增大而增大，回归参数随倾角增大而减小；在节理倾角为45°~90°时，回归参数随倾角增大而减小，回归参数随倾角增大而增大。本试验同样存在=10和=时的关系，故亚临界裂纹扩展参数和的变化规律分别与参数和的变化规律相同。

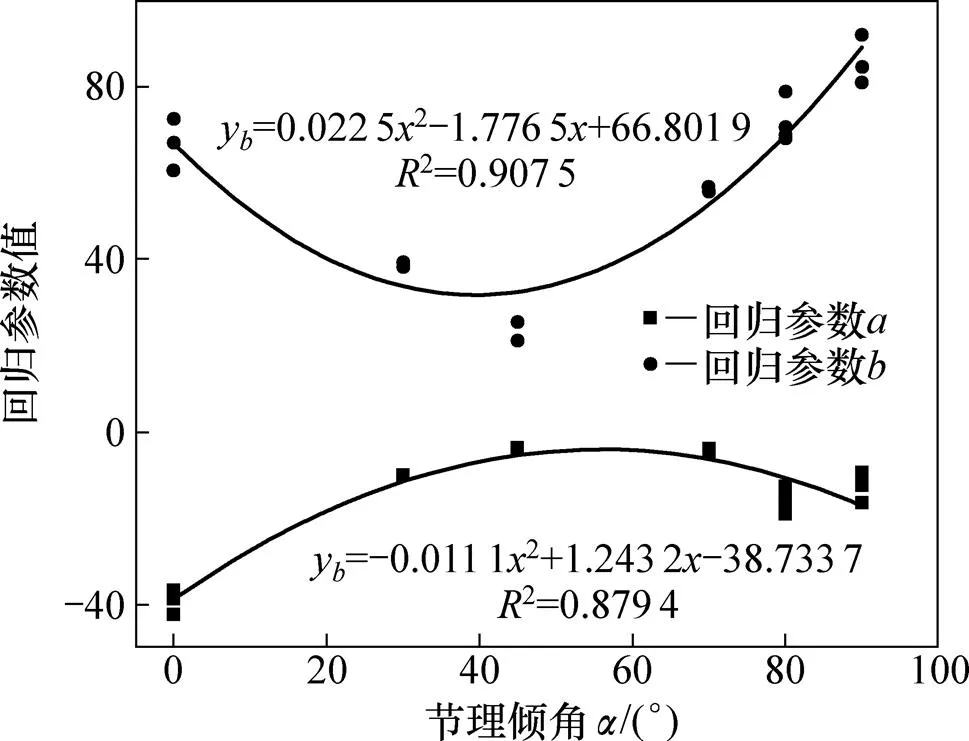
图8 回归参数与节理倾角的关系

3.4 断裂韧度与节理倾角

当节理倾角为0°即节理与短边平行时，板岩断裂韧度IC取得最大值，倾角为45°时取得最小值；当节理倾角小于45°时，IC随角度增大而减小，而当节理倾角大于45°时，IC随角度增大而增大。试样断裂韧度IC与节理倾角的关系见图9，对其进行拟合可得到理想的光滑抛物曲线，且断裂韧度IC与节理倾角满足如下关系式：IC= 0.001 32−0.126 3，2= 0.986 1。

从图9可见：断裂韧度与节理倾角之间的关系符合很好的“U”型抛物线分布。当节理倾角为0°即节理与短边平行时，板岩断裂韧度IC取得最大值；当节理倾角为45°时，断裂韧度IC取得最小值；在节理倾角为0°~45°时，断裂韧度随倾角的增加而减小；在节理倾角为45°~90°时，断裂韧度IC随倾角的增加而增加。

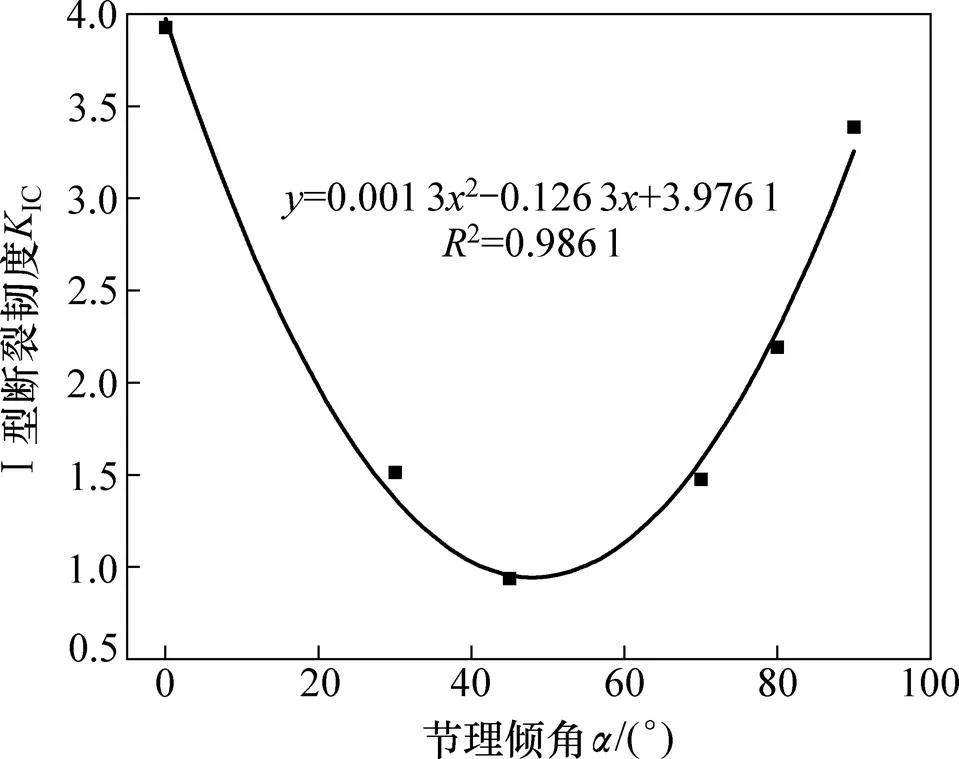
图9 断裂韧度与节理倾角的关系

4 结论

1) 采用双扭测试法研究不同节理倾角的板岩的亚临界裂纹扩展相关规律，在MTS Insight电子拉力试验机上测试试样的亚临界裂纹扩展速度及断裂韧度，得到了试样亚临界裂纹扩展速度与应力强度因子之间的关系和断裂韧度。

2) 对于板岩，其剪切模量不满足各向同性的关系，故需要用横观各向同性理论计算不同节理倾角试样的剪切模量，并对亚临界裂纹扩展速度、应力强度因子和断裂韧度的计算公式进行调整。由于加工原因，尺寸存在较小偏差，采用系数=0.312对其修正是合理的。

3) 采用常位移松弛法所得各组试样的lgI−lg关系都呈现很好的线性规律(系数2均大于0.9)，满足Charles理论。当节理倾角为0°~45°时，回归参数随倾角增大而增大，回归参数随倾角增大而减小；当节理倾角为45°~90°时，回归参数随倾角增大而减小，回归参数随倾角增大而增大，亚临界裂纹扩展参数和的变化规律分别与参数和的变化规律相同。

4) 板岩断裂韧度IC以及松弛应力max均满足“U”型抛物线分布。当节理倾角为0°时，二者均取得最大值；当节理倾角为45°时，两者均取得最小值，且在节理倾角为0°~45°时，两者随倾角增大而减小，在节理倾角为45°~90°时，两者随倾角增大而增大。

[1] 肖洪天, 杨若琼, 周维垣. 三峡船闸花岗岩亚临界裂纹扩展试验研究[J]. 岩石力学与工程学报, 1999, 5(4): 447−450. XIAO Hongtian, YANG Ruoqiong, ZHOU Weiyuan. Testing study of subcritical crack growth of granite at the three gorges shiplock[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 5(4): 447−450.

[2] 罗礼, 孙宗颀. 双扭法研究岩石亚临界裂纹扩展速度和断裂韧度[J]. 岩土工程学报, 1992, 14(3): 40−48. LUO Li, SUN Zongqi. Determination of subcritical crack growth velocity and fracture toughness of rocks by double torsion method[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(3): 40−48.

[3] 袁海平, 曹平, 周正义. 金川矿岩亚临界裂纹扩展试验研究[J]. 中南大学学报(自然科学版), 2006, 37(2): 381−384. YUAN Haiping, CAO Ping, ZHOU Zhengyi. Testing study of subcritical crack growth of ore in Jinchuan mine[J]. Journal of Central South University (Science and Technology), 2006, 37(2): 381−384.

[4] 李江腾, 曹平, 袁海平. 岩石亚临界裂纹扩展试验及门槛值研究[J]. 岩土工程学报, 2006, 28(3): 415−418. LI Jiangteng, CAO Ping, YUAN Haiping. Study on subcritical crack growth and thresholds of rocks[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 415−418.

[5] 李江腾, 古德生, 曹平, 等. 岩石断裂韧度与抗压强度的相关规律[J]. 中南大学学报(自然科学版), 2009, 40(6): 1695−1699. LI Jiangteng, GU Desheng, CAO Ping,et al. Interrelated law between mode-Ⅰfracture toughness and compression strength of rock[J]. Journal of Central South University (Science and Technology), 2009, 40(6): 1695−1699.

[6] 蒋青青, 李江腾, 胡毅夫, 等. 水对亚临界裂纹扩展的影响[J]. 岩土力学, 2008, 29(9): 2527−2530. JIANG Qingqing, LI Jiangteng, HU Yifu, et al. Effects of water on subcritical crack growth[J]. Rock and Soil Mechanics, 2008, 29(9): 2527−2530.

[7] 万琳辉, 曹平, 黄永恒, 等. 水对岩石亚临界裂纹扩展及门槛值的影响研究[J]. 岩土力学, 2010, 31(9): 2737−2742. WAN Linhui, CAO Ping, HUANG Yongheng, et al. Study of subcritical crack growth of rocks and threshold values in different environments[J]. Rock and Soil Mechanics, 2010, 31(9): 2737−2742.

[8] CICCOTTI M. Realistic finite-element model for the double-torsion loading configuration[J]. Journal of the American Ceramic Society, 2004, 83(11): 2737−2744.

[9] GHAZVINIAN A, HADEI M R. Effect of discontinuity orientation and confinement on the strength of jointed anisotropic rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 55(10): 117−124.

[10] LEPLAY P, RÉTHORÉ J, MEILLE S, et al. Three-dimensional analysis of an in situ double-torsion test by X-ray computed tomography and digital volume correlation[J]. Experimental Mechanics, 2013, 53(7): 1265−1275.

[11] CICCOTTI M, GONZATO G, MULARGIA F. The double torsion loading configuration for fracture propagation: an improved methodology for the load-relaxation at constant displacement[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(7): 1103−1113.

[12] ATTIA M S, MAHMOUD A S, MEGAHED M M, et al. Numerical investigations of the stepped double torsion fracture toughness specimen[J]. Engineering Fracture Mechanics, 2010, 77(16): 3359−3367.

[13] KIM H, PARTL M N. Development of a double-torsion fracture test to predict channelized crack behaviors of asphalt concrete[J]. Construction & Building Materials, 2012, 26(1): 694−700.

[14] NARA Y, KANEKO K. Sub-critical crack growth in anisotropic rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(3): 437−453.

[15] NARA Y, KANEKO K. Study of subcritical crack growth in andesite using the double torsion test[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(4): 521−530.

[16] 张久长, 彭立, 许湘华, 等. 横观各向同性岩石弹塑性耦合变形的试验研究[J]. 岩石力学与工程学报, 2011, 30(2): 267−274. ZHANG Jiuchang, PENG Li, XU Xianghua, et al. Experimental study of elastoplastic coupling deformation for transversely isotropic rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 267−274.

[17] 方理刚, 段靓靓, 梁锴, 等. 横观各向同性岩体边坡与预应力锚索框架梁相互作用研究[J]. 岩石力学与工程学报, 2008, 27(1): 135−143. FANG Ligang, DUAN Liangliang, LIAO Kai, et alInteraction between transverse isotropy rock slope and prestressed anchor cable with frame beam support[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 135−143.

[18] 丁皓江. 横观各向同性弹性力学[M]. 杭州: 浙江大学出版社, 1999: 4−7. DING Haojiang. Elasticity of transversely isotropic materials[M]. Hangzhou: Zhejiang University Press, 2005: 1999: 4−7.

[19] 米勒. 岩石力学[M]. 李世平, 冯震海, 译. 北京: 煤炭出版社, 1981: 112−124. MÜLLER L. Rock mechanics[M]. LI Shiping, FENG Zhenhai, trans. Beijing: Coal Press, 1981: 112−124.

[20] 波波夫 E P. 材料力学[M]. 马世谋, 译. 西安: 陕西科学技术出版社, 1986: 56−57. POPOV E P. Mechanics of materials[M]. MA Shimou, trans. Xi’an: Shanxi Science and Technique Press, 1986: 56−57.

[21] LANGE F. 无机非金属材料断裂力学[M]. 张福初, 张金文, 译. 北京: 中国建筑工业出版社, 1982: 32−36. LANGE F. Inorganic nonmetallic material fracture mechanics[M]. ZHANG Fuchu, ZHANG Jinwen, trans. Beijing: China Architecture & Building Press, 1982: 32−36.

[22] 张建平. 横观各向同性材料的剪切模量[J]. 应用数学和力学, 1983, 4(3): 289−296. ZHANG Jianping. Shear modulus of transversely isotropic materials[J]. Applied Mathematics and Mechanics, 1983, 4(3): 289−296.

(编辑 陈灿华)

Experimental study for subcritical crack growth of transverse isotropy rock

WANG Siqing, LI Jiangteng, WANG Congcong

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Subcritical crack growth in transverse isotropy slate was investigated experimentally using constant displacement load relaxation method on MTS insight electronic tensile testing machine. The relationship between the stress intensity factorIand the crack velocityand the fracture toughnessICwere obtained by the test. The growth behavior of subcritical crack was connected with different joint inclination angles. The results show that lgI−lgrelationships are in accordance with linear rule, i.e. when the joint inclination angleis in the range of 0° to 45°,the regression parameterincreases with the increase ofand the regression parameterdecreases with the increase of, and when the joint inclination angleis in the range of 45° to 90°,decreases with the increase ofand the regression parameteris just the opposite. The change laws of subcritical crack growth parametersandare the same with those of the factorsand, respectively. Both the fracture toughnessICand the relaxation maximum loadmaxobey the “U”shaped parabolic distribution. Whenis in the range of 0° to 45°, these two factors decrease with the increase of,and whenis in the range of 45° to 90°,these two factors increase with the increase of. In addition, the two factors reach the maximum value when the angle is 0° and reach the minimum when the angle is 45.

MTS Insight electronic tensile testing machine; transverse isotropy; constant displacement load relaxation method; subcritical crack growth; fracture toughness

10.11817/j.issn.1672−7207.2017.06.026

TU452

A

1672−7207(2017)06−1607−08

2016−07−12；

2016−09−05

国家自然科学基金资助项目(51374246，51304240)；湖南省科技计划项目(2013FJ6002)(Projects(51374246, 51304240) supported by the National Natural Science Foundation of China; Project(2013FJ6002) supported by Plan of Science and Technology of Hunan Province)

李江腾，博士，教授，从事固体力学及岩土工程研究；E-mail：ljtcsu@163.com