冷轧四辊轧机弹性变形在线模型
陈树宗,彭良贵,王力,张殿华
冷轧四辊轧机弹性变形在线模型
陈树宗,彭良贵,王力,张殿华
(东北大学轧制技术及连轧自动化国家重点实验室,辽宁沈阳,110819)
为提高轧机弹跳值的计算精度,开发一种四辊轧机弹性变形的在线计算模型,模型中将轧机弹性变形分为辊系弹性变形和轧机牌坊弹性变形;综合考虑各影响因素,设计辊系和轧机牌坊弹性变形的模型结构。基于所设计的模型结构和测试方案,针对某1 800 mm单机架可逆冷轧机,采用影响函数法得到支撑辊辊径、工作辊辊径、带钢宽度、轧制力和弯辊力等因素对辊系弹性变形的影响,并建立辊系弹性变形在线模型;通过对轧机的现场测试,回归得到轧机牌坊弹性变形模型中的系数,并应用于该机组中。研究结果表明:采用该模型,辊缝设定值的计算偏差可控制在±0.1 mm以内,表明该模型具有较高的计算精度,满足现场控制要求。
轧机弹跳;辊系弹性变形;影响函数法;牌坊弹性变形;轧机刚度;辊缝
在轧制过程中,在轧制力和弯辊力作用下,轧机的轧辊辊系及轧辊轴承座、牌坊等部件会产生弹性变形,这一系列受力部件产生的弹性变形总和称为轧机弹性变形(即轧机弹跳)[1−2]。轧机弹性变形计算主要用于2种情形:一种是用于辊缝设定值的计算,即根据各道次或各机架厚度分配及相应轧制力求该轧机各道次/各机架的辊缝设定值;另一种是根据实测的辊缝和轧制力计算各道次/各机架的出口厚度和AGC调节中的瞬时厚度[3−5]。因此,轧机弹性变形的计算精度直接影响着辊缝设定及带钢出口厚度软测量的精度。目前,通常可采用理论计算法、轧辊压靠法和轧板法等得到轧机弹性变形值,确定轧机轧制力和弯辊力的机座纵向刚度,并仅对带钢宽度影响项进行补偿,而轧辊尺寸和弯辊力等因素对弹性变形的影响在传统模型中没有得到体现[6]。但是,在实际生产中,由于轧辊尺寸、板带宽度等因素变化范围都比较大,并且现场轧制工况与压靠工况有很大不同,因此,传统轧机弹性变形具有一定的局限性[7]。针对传统轧机弹跳计算未充分考虑影响辊系弹跳各影响因素、计算精度低的缺陷,本文作者提出一种理论计算与实验数据回归相结合的四辊轧机弹性变形的计算模型,并应用于某单机架生产过程中。
1 轧机弹性变形的模型结构
在轧机弹性变形中,轧机牌坊和其他机械部件的刚度特性在制造安装后基本不会发生变化,其弹性变形仅仅与轧制力有关;而辊系的弹性变形包括轧辊挠曲及辊间压扁等,在板带生产过程中,辊系的弹性变形会随着轧辊辊径、带钢宽度、轧制力和弯辊力等生产条件的变化而发生改变。
基于上述分析,提出的模型将轧机弹性变形分为辊系弹性变形及轧机牌坊和其他零件的弹性变形,将轧机总弹性变形的模型结构设计为[6]

式中:Total为轧机的总弹性变形,mm;Roll为辊系弹性变形,mm;House为轧机牌坊弹性变形,mm。其中,辊系弹性变形通过基于影响函数法的离线计算和数据回归获得,而牌坊及其他机械部件的弹性变形则通过轧辊全长压靠测试获得的数据进行回归。
2 辊系弹性变形的在线模型
2.1 基于影响函数法的辊系弹性变形计算
影响辊系弹性变形的主要因素有轧辊尺寸、带钢宽度、轧制力及弯辊力等,这些因素对轧机弹跳的影响很难用实测方法得到理想的结果,可采用影响函数法对四辊轧机的辊系弹性变形进行计算[8]。
以普通四辊轧机的上辊系为研究对象,其弹性变形前后的对比如图1所示。图1中,为弹性变形前支撑辊的轴线,为弹性变形后支撑辊的轴线。由于轧制力是通过压下丝杠或液压缸作用在支撑辊的轴承座上,因此支撑辊轴承座在受力中心点产生的位移即为轧机弹性变形。通过分析可知,由于辊系变形引起的支撑辊轴线中心点的位移(即本文所指的辊系弹性变形量Roll),主要由支撑辊中心压扁br、工作辊中心压扁wr以及支撑辊辊径受力点的弹性挠曲变形fl组成,即:

支撑辊间中心压扁br和工作辊中心压扁wr需要将上下辊系的弹性变形进行累加。
图1 四辊轧机辊系弹性变形示意图
Fig. 1 Scheme of rolls elasticity deformation for 4-high mill
影响函数法是一种离散化的方法,其基本思想是将轧辊离散成若干单元,将轧辊所承受的载荷及轧辊弹性变形也按相同单元离散化,应用影响函数的概念先确定对各单元施加单位力时在辊身各点引起的变形,然后将全部载荷作用时各单元引起的变形叠加,得出各单元的变形值。采用影响函数法计算辊系弹性变形[9−12]。
2.2 辊系弹性变形的回归模型
由于影响函数法迭代过程繁琐、计算量大、计算速度慢,因此,不适于作为在线模型实时计算辊系弹性变形[13]。针对该问题,本文采用影响函数法计算出不同因素对轧辊弹性变形的影响规律,利用最小二乘法拟合回归模型中的系数。
影响辊系弹性变形的各因素之间有耦合关系,当工作辊及支撑辊尺寸、带钢宽度等参数确定时,辊系弹性变形量与施加的轧制力和弯辊力有关[14−15]。综合考虑上述因素,将辊系弹性变形分为与轧制力相关的辊系弹性变形、弯辊力相关的弹性变形和回归偏差3部分,模型为

式中:Roll为轧辊辊系弹性变形,mm;为总轧制力,kN;Wb为工作辊总弯辊力,kN;roll为与轧制力相关的辊系弹性变形系数,mm/kN;bend为与弯辊力相关的辊系弹性变形系数,mm/kN;为辊系弹性变形回归偏差,mm。
其中,与轧制力相关的辊系弹性变形系数roll、与弯辊力相关的辊系弹性变形系数bend均与工作辊直径、支撑辊直径及带钢宽度相关。工作辊直径、支撑辊直径及带钢宽度与辊系弹性变形系数之间的关系采用多项式回归方程表达为:

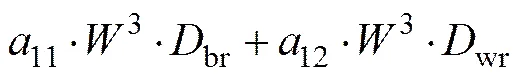
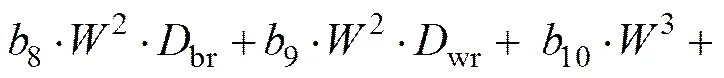
(5)
式中:1~12为roll相关的多项式拟合系数;1~12为bend相关的多项式拟合系数;为带钢宽度,m;br和wr分别为支撑辊直径和工作辊直径,m。
由式(3)~ (5)可以看出,辊系弹性变形系数的多项式回归方程综合考虑了工作辊直径、支撑辊直径及带钢宽度等因素的影响。式中的1~12,1~12和可根据采用影响函数法在不同参数下计算的辊系弹性变形值进行回归获得。
3 轧机牌坊弹性变形的在线模型
在轧制过程中,轧件作用到轧辊上的全部轧制力通过轧辊轴承、轴承座、压下螺丝及螺母传给轧机牌坊,该部分受力后所产生的垂直方向的弹性变形直接影响着板带材的轧制精度。
3.1 轧机牌坊弹性变形的模型结构
轧机牌坊弹性变形的受力情况非常复杂,且有关零件的接触面间存在间隙,目前没有精确的理论计算方法。同时,考虑到轧机牌坊和其他机械部件的刚度特性在制造安装后不会发生变化,因此确定牌坊弹性变形模型中的系数可以通过轧辊全长压靠法来获得,且无需重复测量。
轧机牌坊及机械部件的弹性变形与轧制力之间不是简单的线性关系。在低轧制力段,由于各机械部件之间存在间隙和接触变形,轧机牌坊弹性变形和轧制力之间的关系为非线性;在高轧制力段,轧机牌坊弹性变形和轧制力之间趋近线性关系[16]。基于上述分析,将轧机牌坊弹性变形的模型结构设计为

式中:H为轧机牌坊刚度系数,kN/mm;ΔH为牌坊弹性变形回归参数,mm;H为牌坊弹性变形模型参数,kN/mm。
3.2 轧机刚度测试与模型参数拟合
在轧辊全长压靠过程中,通过数据采集系统采集轧制力及对应的辊缝值,在经过数据处理后可获得不同轧制力下的轧机弹性变形。测量的轧机弹性变形既包含牌坊弹性变形,还包括辊系弹性变形。其中,辊系弹性变形采用已经建立的辊系弹性模型计算,将总的轧机弹性变形减去辊系弹性变形,便可得到轧机牌坊弹性变形,进而通过数据拟合可得到轧机牌坊弹性变形模型中的系数。
根据上述分析,设计测试方案和数据处理流程如图2所示,具体步骤为:
1) 轧机全长压靠准备。以固定的转速运转轧机一段时间,使轧辊、机械设备及现场润滑等均达到正常轧制时的状态。

图2 轧机弹性变形测试流程图
2) 轧机刚度测试。无带钢情况下进行轧辊全长压靠,轧制力按照一定的步幅从0 kN增加到最高值,之后再按照相同步幅减小至0 kN,压靠时确保弯辊力和轧辊速度保持恒定。在压靠过程中,通过数据采集系统详细记录轧制力、弯辊力及对应的辊缝值。
3) 增量化处理。设置轧制力的基准值0,该轧制力下的辊缝值0作为基准值;选取大于该基准轧制力的数据,定义增量轧制力为(实测轧制力−0);增量辊缝为(实测辊缝−0),对得到的轧制力增量值、辊缝增量值进行数据处理,剔除坏点。
4) 采用式(3)~ (5)计算辊系弹性变形,计算时带钢宽度等效于工作辊辊身长度;将轧机总弹性变形减去辊系弹性变形,得到轧机牌坊弹性变形。
5) 在获得轧机牌坊弹性变形曲线的基础上,对轧机牌坊弹性变形回归模型中的系数进行拟合。
4 现场应用与算例分析
本文提出的轧机弹性变形计算算法已通过C语言编程实现,并已应用在某1 800 mm单机架可逆冷轧机过程控制模型设定系统中。在计算辊缝设定值时,首先根据轧制力、弯辊力、带钢宽度及轧辊尺寸等参数计算轧机弹跳变形,进而求出辊缝值。下面基于该1 800 mm单机架可逆轧机,给出具体算例和测试结果,并结合现场数据验证该模型的计算精度。
4.1 辊系弹性变形在线模型的算例与分析
针对选取的轧机,在采用影响函数法计算时,辊系弹性变形各影响因素如表1所示。
在采用影响函数法计算辊系弹性变形过程中,支撑辊直径分别为1.300,1.320,1.340,1.360,1.380,1.400,1.420和1.450 m;工作辊直径分别为0.420,0.430,0.440,0.450,0.460,0.470,0.480和0.490 m;带钢宽度分别为0.800,1.000,1.200,1.400,1.600和1.800 m;总轧制力分别为5,8,11,14,17,20和23 MN;工作辊总弯辊力分别为−3,−2,−1,1,2和3 MN。

表1 采用影响函数法计算辊系弹性变形时的参数
图3所示为采用影响函数法计算得到的不同参数下的辊系弹性变形。由图3可见:在带钢宽度、辊系尺寸固定时,辊系的弹性变形与轧制力、弯辊力均成线性关系,与轧制力和负弯辊力成正比、与正弯辊力成反比;在轧制力和正弯辊力固定时,随着支撑辊辊径、工作辊辊径及带钢宽度的增加,辊系的弹性变形减小,这与现场实际轧制所反映出的规律是相吻合的。
将影响函数法计算得到的辊系弹性变形作为拟合源数据,通过最小二乘法获得辊系弹性变形回归数学模型中1~12,1~12和等系数的具体数值,如表2所示。
模型参数拟合后,将获得的辊系弹性变形回归模型中的系数保存至相应的配置文件中,从而应用式(3)~(5)求解出不同条件下的辊系弹性变形。
4.2 轧机牌坊弹性变形的现场测试
根据轧机牌坊弹性变形测试方法,对某1 800 mm单机架可逆冷轧机进行刚度测试。在轧辊全长压靠过程中,轧制力按照200 kN/s的步幅从0 kN增加到 17 000 kN,之后再按照相同步幅减小至0 kN,压靠过程中轧辊速度保持在100 m/min,工作辊正弯辊力保持为300 kN,数据的采样周期为200 ms。
设置轧制力基准值0为3 MN,对测量的轧制力、辊缝值进行增量化处理,并剔除坏点,得到轧机总弹性变形实测曲线,如图4(a)所示;通过模型计算的辊系弹性变形如图4(b)所示;将总的辊缝增量减去辊系弹性变形增量得到轧机牌坊弹性变形增量,如图4(c)所示。从图4可见,轧机弹性变形在低轧制力段呈现明显的非线性、且刚度系数较小,而在高轧制力段趋于线性关系,这是由轧机牌坊及零部件间的接触变形和间隙造成的;而辊系弹性变形与轧制力成线性关系,在轧辊尺寸固定时,辊系刚度系数为定值。
在获得轧机牌坊弹性变形曲线的基础上,可对牌坊弹性变形回归模型中的系数进行拟合,轧机牌坊弹性变形拟合曲线如图4(d)所示;在参数回归时必然存在拟合误差,误差曲线如图5所示。可见:高轧制力段的拟合误差在±0.02 mm内。

(a) 辊系变形与轧制力和支撑辊辊径关系;(b) 辊系变形与轧制力和工作辊辊径关系;(c) 辊系变形与轧制力和带钢宽度关系;(d) 辊系变形与弯辊力和支撑辊辊径关系;(e) 辊系变形与弯辊力和工作辊辊径关系;(f) 辊系变形与弯辊力和带钢宽度关系

表2 模型系数拟合值
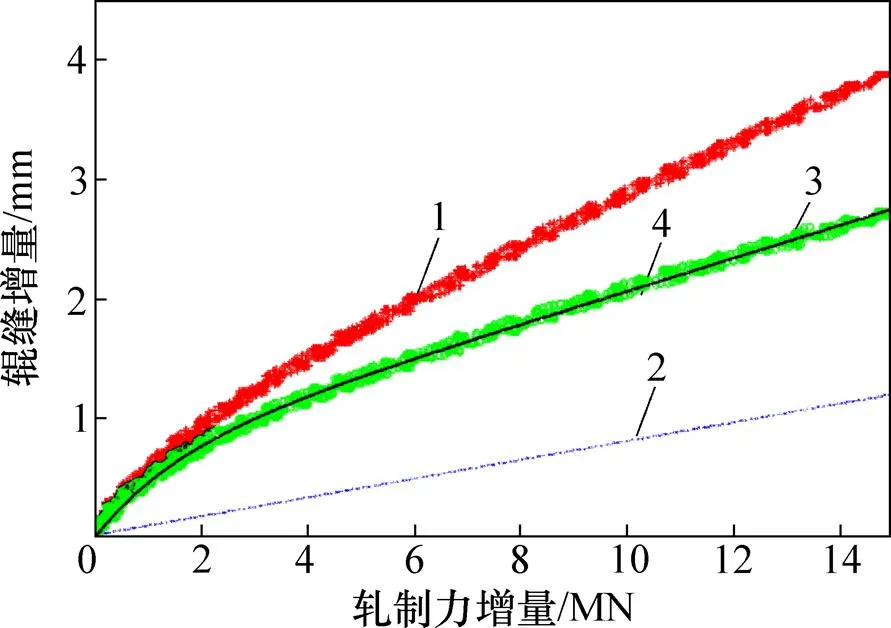
1—轧机总弹性变形实测值;2—辊系弹性变形计算值;3—轧机牌坊弹性变形增量;4—轧机牌坊弹性变形拟合值。
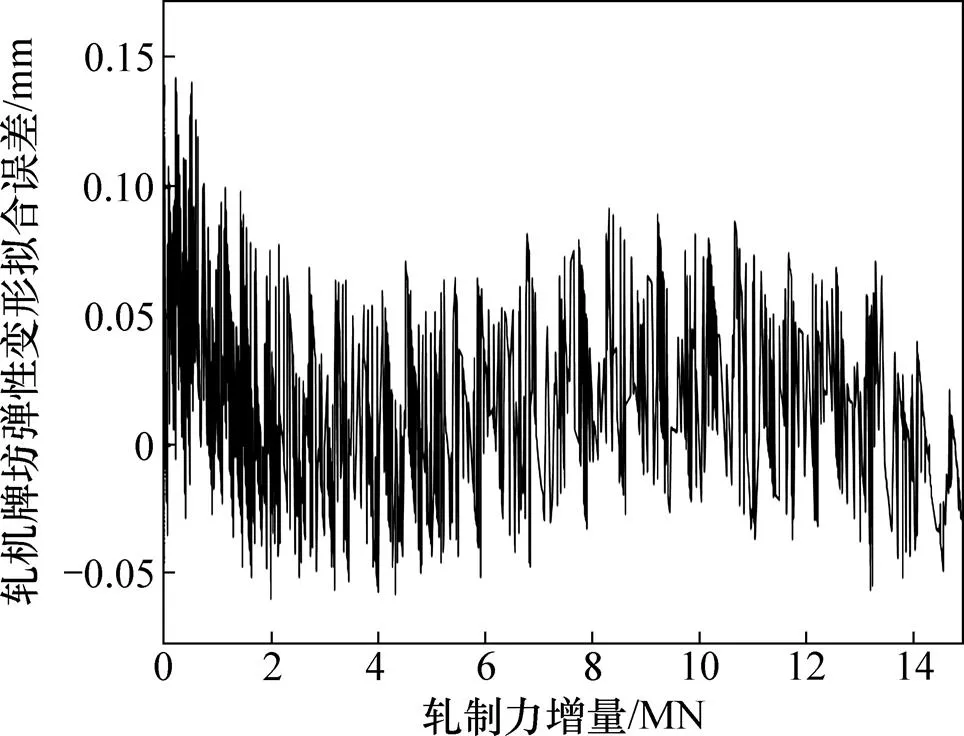
图5 轧机牌坊弹性变形模型的拟合误差
根据最小二乘法拟合得到模型中的系数H= 6 877 kN/mm,ΔH=0.709 1 和H=1 582,因此,轧机牌坊弹性变形回归模型如下:
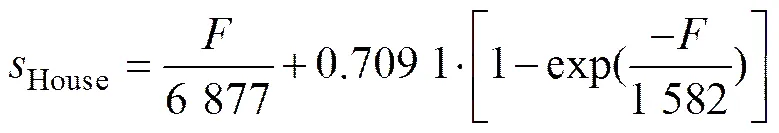
4.3 轧机弹性变形模型的现场应用
对于冷轧单机架模型设定系统而言,轧机弹性变形模型主要用于辊缝设定值的计算。辊缝模型描述的是辊缝与出口带钢厚度之间的关系,其设定过程是先确定带钢入口厚度和出口厚度,然后计算出相应的轧制力和弯辊力,进而根据轧机弹性变形模型计算出相应的弹跳值,采用的公式为
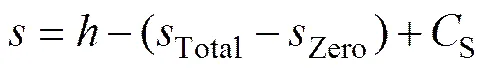
式中:为轧机辊缝设定,mm;为出口带钢厚度,mm;Total为轧机总弹性变形,mm;Zero为调零轧制力下的弹性变形,mm;S为辊缝修正系数,mm。
采用某1 800 mm单机架可逆轧机压下规程的辊缝设定结果和厚度控制效果来分析轧机弹性变形模型的计算精度。表3所示为钢种CQ、宽度为1 250 mm、入口厚度为2.30 mm、出口厚度为0.39 mm的冷轧带钢在高速稳定状态下的模型设定值和现场实测值的对比。由表3可以看出,模型设定轧制力、弯辊力和辊缝的设定值和实测值均非常接近,其中辊缝计算偏差控制在±0.1 mm以内,优于采用传统轧机弹跳模型计算的辊缝计算精度。厚度偏差曲线如图6所示。由于给定了精准的初始辊缝设定值,厚度偏差超过±2%的头尾带钢长度仅为30 m;在稳速轧制时,该带钢全长厚度精度控制在±1%以内。现场应用表明该模型具有较高的精度,满足现场控制要求。
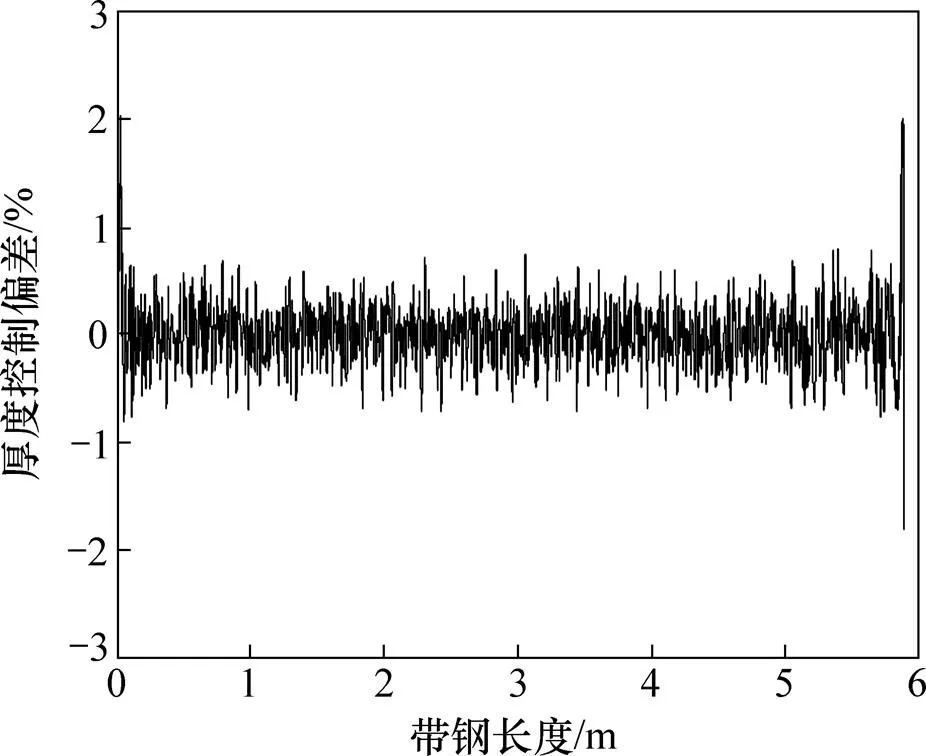
图6 整条带钢长度上的厚度偏差曲线

表3 模型设定值和实测值的对比
注:*数据为实测值。
5 结论
1) 开发了新型的轧机弹性变形在线计算模型,将轧机弹性变形分为辊系弹性变形和轧机牌坊弹性变形2部分,综合考虑各影响因素,给出了相应的在线模型结构和计算方法。
2) 将影响函数法应用于辊系弹性变形的计算,针对某单机架冷轧机,分析了支撑辊辊径、工作辊辊径、带钢宽度、轧制力和弯辊力等因素对辊系弹性变形的影响;在此基础上,建立了辊系弹性变形的在线回归模型。
3) 基于某单机架可逆冷轧机,根据现场实际的刚度测试数据,回归得到了轧机牌坊弹性变形模型,高轧制力段的拟合误差控制在±0.02 mm内。轧机弹性变形在低压靠轧制力段呈现明显的非线性且刚度系数较小,在高轧制力段趋于线性关系;而辊系弹性变形与轧制力、弯辊力成线性关系。
4) 开发的轧机弹性变形计算模型已成功应用于某1 800 mm单机架可逆冷轧机组中,通过现场辊缝设定值和厚度控制效果验证该模型具有较高的精度,辊缝计算偏差控制在±0.1 mm以内,厚度偏差超出±2%范围的头尾带钢长度仅为30 m,该模型能满足在线控制的要求。
[1] Vladimir G. Flat-rolled steel processes[M]. New York: CRC Press, 2009: 335−338.
[2] LENARD J G. Primer on flat rolling[M]. 2nd ed. Tokyo: Tokyo Press, 2007: 92−98.
[3] LIU Shujian, WU Bocheng. Optimum design of rolling schedule for tandem cold mill using SLPSO[J]. Applied Mechanics and Materials, 2012, 101/102: 443−446.
[4] WANG Qiaoyi, JIANG Zhengyi, ZHAO Jingwei. Multi-factor coupling system characteristic of the dynamic roll gap in the high-speed rolling mill during the unsteady lubrication process[J]. Tribology International, 2013, 67(4): 174−181.
[5] 龚殿尧, 徐建忠, 袁方成. 四辊轧机不对称刚度条件下轧辊弹性变形的研究[J]. 东北大学学报(自然科学版), 2012, 33(11): 1586−1590. GONG Dianyao, XU Jianzhong, YUAN Fangcheng. Study on roll elastic deformation asymmetrical 4-high mill stiffness[J]. Journal of Northeastern University (Natural Science), 2012, 33(11): 1586−1590.
[6] 曹建国, 张杰, 张少军. 轧钢设备及自动控制[M]. 北京: 化学工业出版社, 2010: 46−49. CAO Jianguo, ZHANG Jie, ZHANG Shaojun. The steel rolling equipment and automatic control[M]. Beijing: Chemical Industry Press, 2010: 46−49.
[7] WANG J S, JIANG Z Y, TIEU A K, ea al. A flying gauge change model in tandem cold strip mill[J]. Journal of Materials Processing Technology, 2008, 204(1/2/3): 152−161.
[8] FINSTERMANN G, SEILINGER A, NOPP G, et al. Comparison of 4-high and 6-high mill-stand technology in cold-rolling mills[J]. Metallurgical Plant Technology, 2007, 30(1): 54−61.
[9] 董永刚, 苏玉龙, 张岩岩. 配备组合式支承辊的四辊冷轧机辊系弹性变形数学模型[J]. 中南大学学报(自然科学版), 2013, 44(6): 2298−2303. DONG Yonggang, SU Yulong, ZHANG Yanyan. Mathematical model of elastic deformation of cold reduction mill equipped with composite back-up roll[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2298−2303.
[10] 徐建忠, 张风琴, 龚殿尧, 等. 四辊轧机轧辊弹性变形解析模块的开发[J]. 轧钢, 2003, 20(2): 8−11. XU Jianzhong, ZHANG Fengqin, GONG Dianyao, et al. Development of calculation module of rolls elasticity deformation in 4-h mill[J]. Steel Rolling, 2003, 20(2): 8−11.
[11] 白金兰, 王军生, 王国栋, 等.六辊轧机辊间压力分布解析[J]. 东北大学学报(自然科学版), 2005, 26(2): 133−136. BAI Jinlan, WANG Junsheng, WANG Guodong, et al. Analysis of roll force distribution between rolls on a six-high mill[J]. Journal of Northeastern University (Natural Science), 2005, 26(2): 133−136.
[12] 王国栋. 板形控制和板形理论[M]. 北京: 冶金工业出版社, 1986: 35−40. WANG Guodong. Flatness control and flatness theory[M]. Beijing: Metallurgical Industry Press, 1986: 35−40.
[13] LI Haijun, XU Jianzhong, WANG Guodong, et al. Development of strip flatness and crown control model for hot strip mills[J]. Journal of Iron and Steel Research (International), 2010, 17(3): 21−27, 45.
[14] 董立杰, 何安瑞, 宋勇, 等. 热带钢轧机辊系纵向刚度在线计算模型[J]. 北京科技大学学报, 2009, 31(11): 1452−1456. DONG Lijie, HE Anrui, SONG Yong, et al. Online calculation model of roll vertical stiffness in a hot rolling-mill[J]. Journal of University of Science and Technology Beijing, 2009, 31(11): 1452−1456.
[15] SUN Dengyue, ZHANG Yuanfang, ZHA Xianwen, et al. Study on the roller’s thermal stress of the liquid core heavy reduction rolling mill[J]. Applied Mechanics and Materials, 2010, 29/30/31/32: 1380−1384.
[16] 黄新, 佟琨, 宋锦春, 等. 基于ANSYS有限元法的5 500 mm四辊轧机牌坊分析[J]. 冶金设备, 2012(1): 46−49. HUANG Xin, TONG Kun, SONG Jinchun, et al. Analysis of the house of the 5 500 mm four-high mill based on ANSYS finite element method[J]. Metallurgical Equipment, 2012(1): 46−49.
(编辑 赵俊)
Online model research for elastic deformation of 4-high cold mill
CHEN Shuzong, PENG Lianggui, WANG Li, ZHANG Dianhua
(The State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China)
In order to improve the mill spring calculation accuracy, a new online elastic deformation model for 4-high cold mill was put forward. In the model, the mill elastic deformation was divided into two parts, i.e. rolls elastic deformation and mill housing elastic deformation. Combining all the influence factors, the model structure of rolls and mill housing elastic deformation were designed. Based on the proposed model structure and test scheme, aiming at a 1 800 mm single-stand reversible cold mill, the effect of every factors on the rolls elastic deformation, such as back-up roll diameter, work roll diameter, strip width, rolling force and bending force, were obtained by means of influential function method, and the online model of rolls elastic deformation was established. Based on the actual test data of a single-stand cold mill, the coefficients of mill housing elastic deformation model were obtained, and the proposed mill elastic deformation model was applied in this mill. The results indicate that the calculation deviation of roll gap value is within ±0.1 mm, which shows that the model is accurate and it can meet the requirement of online process control.
mill spring; rolls elastic deformation; influential function method; mill housing elastic deformation; mill rigidity; roll gap
10.11817/j.issn.1672−7207.2017.06.004
TG333.5
A
1672−7207(2017)06−1432−07
2016−06−07;
2016−09−01
国家自然科学基金资助项目(51074051);辽宁省博士启动基金资助项目(20131033)(Project (51074051) supported by the National Natural Science Foundation of China; Project (20131033) supported by the Doctoral Scientific Research Foundation of Liaoning Province)
陈树宗,博士,从事轧制过程自动化领域的研究;E-mail:chenshuzong10@163.com

