魔方里的数学密码

魔方于1974年由匈牙利人鲁毕克发明。它能征服全世界，与匈牙利众多伟大的数学家（例如冯·卡门、冯·诺伊曼以及5位获得过沃尔夫奖和阿贝尔奖的数学家）有很大关系——匈牙利的数学家们通过1978年的世界数学家大会，把魔方推广到了全世界。那么，这个小小的立方体到底与数学有怎樣的关系呢？一起来看看吧！

鲁毕克是布达佩斯工艺美术学院的教师，主要讲授外形研究与画法几何学。为培养学生的三维想象力，他于1974年设计、制造了三阶魔方，并将其称为Magic Cube。Magic Square（即幻方）是数学的一个分支，所以Magic Cube早年被译为幻立方体。1979年后，Magic Cube改为Rubiks Cube，成为现在数学中的专有名词。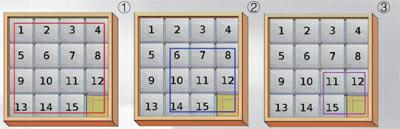

魔方起源—15子棋

追溯魔方的起源，不免要谈到1880年时美国的15子棋。15子棋棋子和魔方小块运动的数学原理是相同的。如图①～③所示，通过滑动周围的棋子，棋盘中的空格可以沿着图示的线路转动起来，这和魔方小块的转动是一样的。

延伸阅读：重排九宫图

15子棋的前身是重排九宫图，重排九宫游戏棋最早出现在元代。在宋代，九宫图被叫作纵横图（即幻方）。杨辉是南宋研究纵横图的著名数学家。《易传·系辞》曰：“河出图，洛出书，圣人则之。”洛书是中国5000年前的产物，是幻方的先祖。

“离家”和“回家”

魔方一路走来，能风靡全球、经久不衰，和其中蕴藏的数学密码有密切关系。那么，魔方里到底有什么数学密码呢？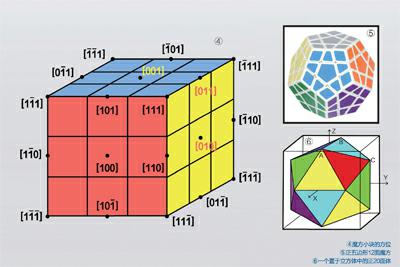

我们先简单讨论魔方的“离家”和“回家”问题。当你拿着一个处于原始状态的魔方（即魔方处于复位状态），我们说魔方是在“家里”。如果你是个新手，扭转魔方时，不要让魔方“离家”太远，可以靠直觉使魔方“回家”。

首先，随便选择一面，转动魔方1步，转角可以是90°或180°或270°。对于魔方“离家”1步远的情况，不难计算其状态共有6×3=18个。换句话说，即每个面分别转动90°或180°或270°，6个面共有18个状态。为了叙述方便，我们分别用F、R、U、B、L、D表示魔方的前面、右面、上面、后面、左面和下面。

然后，让魔方“离家”2步远，即先转动一个面，再转动另外一个面。如果用符号表示就是：

F（R、U、B、L、D）；R（F、U、B、L、D）；U（F、R、B、L、D）；

B（F、R、U、L、D）；L（F、R、U、B、D）；D（F、R、U、B、L）。

上面的组合共有30组，每个字母有3个可选择的转角，共有30×3×3=270个状态。需要强调的是，我们是在计算魔方的状态数，这涉及魔方的几何问题。例如，组合FB和BF给出的魔方状态是完全相同的。因为F面和B面平行，转动的先后次序不影响魔方的状态。因此，FB和BF，RL和LR，UD和DU分别相同，要去掉3个，剩下27个组合。那么，27×3×3=243，即魔方“离家”2步远，共有243个状态。魔方“离家”2步远时，我们也可以轻松让魔方“回家”。

按照以上组合操作和比较魔方状态的方法，可以计算出：

魔方“离家”3步远，共有3，240个状态；

魔方“离家”4步远，共有43，239个状态；

魔方“离家”5步远，共有574，908个状态。

如果随意让魔方离家5步远，而你仅仅用5步就能把它复位，那么你就是地地道道的天才。换句话说，面对574，908个魔方状态，仅凭直觉用5步将这些魔方复位，世界上还没有人能够做到。

如果把魔方离家的所有状态求和，再加上一个在家的状态，这个数就是43，252，003，274，489，856，000。

2010年，谷歌的一个团队计算出魔方离家21步远的状态为0，也就是说，魔方离家最远是20步。于是，他们宣布：对于任何一个被搅乱了的魔方，都可以在20步以内将其复原。

目前，复位三阶魔方最快者所用时间不到5秒，但是他们需要转动魔方50多次。2017年3月有报道称，一位德国工程师设计的机器人，复位魔方只需0.637秒，仅需转动魔方21次。

魔方小块的方位

魔方里用到的数学既简单又撩人。

三阶魔方有8个角块、12个边块和6个心块，描述这些小块的空间方位有很简单的方法。如图④所示，用数组<111>描述角块，用数组<110>描述边块，用数组<100>描述心块。如果用负号（数字1上加横线），让这些数组中的三个数排列组合：<111>有8种情况，和魔方的角块一一对应；<110>有12种情况，和魔方的边块一一对应；<100>有6种情况，和魔方的心块一一对应。用这种方法，还可以描述2阶魔方、高阶魔方和某些异型魔方。

12面魔方有12个心块、20（=5×12÷3）个角块、30（=5×12÷2）个边块。如果能计算出这些小块的空间坐标，就可以建立数学模型来描述这些小块的运动。

我们可以借助三阶魔方，计算出12面魔方各小块的空间坐标。如图④所示，魔方12条棱边中心的黑点，分布在6个面上，每面有2个。例如，蓝色面的前后两个黑点属于该面，黄色面上下两个黑点属于该面，以此类推。图④中魔方的边长由2个单位压缩到1.618，每个面上的黑点之间的距离压缩到1，如图⑥所示。把这些黑点近邻地连接起来，就构成一个正20面体，同时，我们得到了12个顶点的坐标。例如，A、B、C三点的坐标分别为（0.5，0，0.809）、（-0.5，0，0.809）、（0，0.809，0.5）。endprint

参照图⑥的坐标系，可以把12个顶点的坐标标注在12面魔方的心块中心，一一对应。根据12面魔方心块的坐标，经简单的几何計算，可以求出20个角块和30个边块的空间坐标，然后就可以计算12面魔方转动后小块坐标的变化。参照魔方的“离家”和“回家”，12面魔方也可以按步找到和三阶魔方的对接点。

5个公式复位法

魔方的复位方法很多，下面给大家介绍最简单的“5个公式复位法”。

首先，根据直觉能力，复位魔方的第一层—通过魔方“离家”和“回家”操作，可以轻松培养这种直觉能力。然后，根据“牛郎和织女的故事”复位魔方的第二层（可以参看《魔方和数学建模》视频公开课）。最后，根据5个公式，复位魔方的第三层。

本文给出操作序列的两种表达形式：①6个字母表示魔方的6个面，带“”表示逆时针转动90°，否则为顺时针转动90°，带“2”表示转动180°；②此种表达基于笛卡儿坐标系，坐落于正方向的面用右手操作，转动方向满足右手规则，坐落于负方向的面用左手操作，转动方向满足左手规则。

魔方里所包含的数学知识，如同浩瀚海洋的沙滩海岸，浅的地方谁都可以来玩，包括幼儿园的小朋友，不需要什么装备；深的地方更好玩，但需要一些数学上的技能。群论是研究魔方的主要数学理论，同样，魔方也是学习群论的最好模型。近年来兴起的几何代数学，可以用来研究魔方问题，同样，通过玩魔方也可以学习几何代数学。

知识链接 盲拧的秘密

三阶魔方是变种魔方和高阶魔方的基础，三阶魔方的复位是魔方的经典内容。那些能快速复位魔方的人，除了勤学苦练之外，他们都具有非凡的记忆力。手法相同的情况下，记忆的公式越多，复位的速度就越快。特别是那些盲拧的人，没有非凡的记忆力是不可能将魔方复原的。

动手之前，他们要长时间观察魔方，其目的是为了让角块和边块“对号入座”，编码相关的操作序列。以角块为例，来说明蒙眼复位魔方的基本方法。若8个角块分别为ABCDEFGH，原始状态为A1B2C3D4E5F6G7H8占位，而现在的状态是A2B1C4D3E8F6G7H5，对比原始状态可知：A和B、C和D、E和H分别交换了位置。对于以上魔方，在操作之前要分别记住交换A和B、C和D、E和H所需要的操作公式，那么蒙眼后就可以把魔方复位。

作者简介

李世春，获清华大学材料学博士学位，中国石油大学（华东）材料系退休教授，长期从事魔方研究，先后出版了《魔方及其应用》《魔方的科学和计算机表现》和《魔方里的科学和文化》等著作。endprint