基于振荡中心电压的对称性故障开放新判据
李 斌 郑玉平 陈瑞俊
基于振荡中心电压的对称性故障开放新判据
李 斌1郑玉平2陈瑞俊1
(1. 江苏省电力公司检修分公司,南京 210000; 2. 南瑞集团,南京 210000)
本文利用计算电压为一余弦函数且在系统振荡时等于振荡中心电压、而在三相短路时的其值不大于电弧电阻上的压降的特征,并考虑在振荡时的一个较短的时间内,可认为计算电压是匀速变化的特点,提出了一种振荡中对称性故障开放判据。当计算电压在0附近小区间内停留的时间超过计算获得的预期时间时,说明发生了对称性故障,开放保护动作。新判据与振荡周期自适应,易于整定,易于实现。仿真结果证明了该判据的正确性和有效性。
线路保护;振荡闭锁;对称性故障;余弦函数;自适应
并列运行的系统或发电厂失去同步的现象称为失步振荡。电力系统振荡时,系统两侧等效电动势的夹角可能在0°~360°范围内周期性变化,从而使得系统内各点的电压、线路电流、功率大小和方向呈周期性变化,以这些量作为测量对象的各种保护的测量原件,就可能误动[1-3]。因此,当系统发生振荡时应由振荡闭锁将距离保护闭锁,使得距离保护不会误动。但是,当振荡中再发生短路时,振荡闭锁应开放保护,允许保护切除故障。对于不对称故障,可利用序电流比值法或三相电流大小不等和零序电流的大小来识别;对于对称性故障,目前常用振荡中心电压1cos()[4-5]、振荡中心电压变化率d1cos()/d或者利用测量阻抗变化率dm/d来实现[6-7]。也有学者提出了利用线路两端电压夹角[8]或波形特性[9]来判别,但当系统等效阻抗较大而线路阻抗较小时,计算较复杂且计算的误差较大,该判据可能失效。相关学者也利用系统功角与失稳条件的边界判据相结合,在功角小于整定值时允许距离保护在振荡闭锁期间快速开放[11],但此判据中失去稳边界的确定缺乏理论支持。也有学者提出了利用暂态量对距离保护改进[12-14],但振荡期间仍无法保证正确动作。利用线路两端故障量的纵联保护[15-16]在系统振荡时不会误动作,但其通道的可靠性仍然有待提高[17],利用单端电气量的距离保护仍然具有优越性。现阶段对称性故障开放判据多采用固定延时的原理构成[2],共有的缺点是开放时需经较长的延时,约150ms左右。
本文利用计算电压os的数值在振荡时等于振荡中心电压,而在三相短路时的值不大于电弧电阻上的电压的特征,并考虑一个较短的时间内,可认为振荡是匀速变化的特点和余弦函数的数学特征,提出了一种振荡中对称性故障开放判据。本判据根据os相对于时间的变化率,计算推测os在0附近某一区间内停留的时间,并将传统判据中的固定延时替换成此推测时间,若os在推测时间内一直满足条件,则开放保护。三相故障时os快速跌落,变化率较大,计算获得的预测时间远远小于传统的固定延时,提高了保护开放速度。本文提出的判据具有自适应性,可实时根据振荡速度来确定开放保护所需要的时间,有利于保护快速切除三相故障。
1 Uos的变化特点
定义计算电压os如下,os为一余弦函数。

式中,1为正序电压,是正序电压与正序电流间的夹角,为线路阻抗角的余角。
os具有如下特征[3-4]:系统振荡时,os与振荡中心电压相等,振荡中心电压随着两侧电动势夹角的变化而变化,其变化规律为os=||cos(/2),为关于功角的余弦函数。发生三相短路时,os的数值快速跌落并保持在不大于弧光电阻上的电压值。此外,理论上可以证明电弧在电流超过100A时其电弧电阻上压降与短路电流无关,电弧电阻上的电压一般不会超过额定电压的5%[18]。
根据以上特征,现阶段国内保护厂家使用较普及的振荡中对称性故障开放判据可描述[2]如下:
1)在150ms内一直满足-0.03N<os<0.08N时,开放保护。
2)在500ms内一直满足-0.1N<os<0.25N时,开放保护。
判据的逻辑图如图1所示,1、2为判据中设定的边界区间。在系统振荡时发生故障,或正常运行的系统在受到扰动后经短时开放判据[2]开放160ms之后又发生区内故障时,保护需要利用对称性故障开放判据经固定延时(150ms/500ms)后才能开放,降低了保护的速动性。

图1 对称性判据逻辑图
2 基于振荡中心电压的对称性故障开放判据
振荡是一个机电暂态过程,在一个较短的时间内,功角的变化可以看作是匀速的。由式(1)可知,振荡时计算电压os是关于功角的余弦函数。对于余弦函数cos(p),其值在[-0.1, 0.1]区间内变化时,其变化率变化区间为[0.995, 1],则可近似认为 cos(p)在此区间内是匀速变化的。由余弦函数的数学特征可知,当os在[-0.11, 0.11]区间内变化时,可看作是匀速变化的。
利用此种特征,通过测量在每个振荡周期中在进入此确定区间的时刻os对时间的变化率,可以计算确定os在此区间内所停留的时间,此计算获得时间与os的变化速率,即振荡周期自适应。在发生三相故障时,os的数值快速跌落并保持在电弧电阻电压以下,故障时os对时间的变化率较大,计算os在此范围区间所停留的时间短。
利用上述特性,本文提出了新的振荡中对称性故障开放判据,逻辑图仍如图1所示,但使用计算os在设定区间所停留的时间3替代固定延时。当os在时间3内一直满足条件时,说明发生了故障,可开放保护动作。
假设1为os在区间[1,2]内实际停留的时间,2为os在区间[1,2]内理论计算停留的时间。由上述分析可知,若实际停留的时间1超过理论计算停留的时间2,说明发生了故障,则开放保护。鉴于利用了os数值的变化特性,在考虑一定的裕度情况下,本文中1=-0.06N,2=-0.08N。由于1、2数值较为接近,因此在[1,2]是所确定的区域内,可以认为os是匀速变化的。若记os进入区间[1,2]时的变化率为T=dos/d,则可较准确地推断os在区间[1,2]内停留的时间2,计算式为

如果考虑计算误差的影响,实际测得os在此范围内的时间可能大于计算时间2,导致保护误开放。为了保证计算时间始终不小于实际停留的时间,设定计算时间为
(3)
式中,为可靠系数,设定范围可取为1.5~2.0,以保证可靠性;0为一大于0的实数,保证3在任何时刻都大于0。
由以上分析可知,在系统振荡时,在确定区间[1,2]内,可认为os的变化速度恒定,根据os开始进入区间[1,2]时的变化率,可以准确地计算预测os在该区间停留的时间,计算时考虑了一定的可靠系数,os在该区间实际停留的时间将短于计算时间,新判据不满足,保护不会误动,具有可靠性。
在系统振荡或正常运行、发生三相故障时,os数值快速跌落至并保持在电弧电压以下,且os数值的变化特性不受系统结构和运行方式的影响。由前述分析可知,与利用系统振荡时os的变化率计算获得的固定延时相比,故障时os在进入区间[1,2]时的变化率较大,按式(3)计算可得到3远小于。当os在[1,2]区间内停留的时间超过计算时间3时,判据满足,可开放保护,动作速度快。发生故障时的计算时间3与发生故障时os的数值有关,短路前系统功角越小,os的值越大,故障时os数值的跌落速度越大,判据开放所需延迟时间越短。此种特性使得正常运行的系统在受到扰动后短时160ms之后又发生区内故障时,保护开放所需经历的延时由固定时间减短为3,提高了保护的开放速度。
3 仿真试验
为了验证本文所述判据的正确性,以PSCAD输出的波形数据配合Matlab软件进行仿真分析。试验模型采用电压等级为220kV的100km双机系统模型,系统架构如图2所示。

图2 仿真系统结构图
仿真系统的参数为:
线路电压等级220kV。
M侧:正序阻抗M1=10.6∠88°,零序阻抗M0= 15.3∠88°。
N侧:正序阻抗N1=10.6∠88°,零序阻抗N0= 10.6∠88°。
线路参数见表1。

表1 220kV输电线路典型参数(100km)
距离保护元件:使用以正序电压为极化电压的阻抗继电器动作特性,判别方程使用比相式判别方程实现。
算法:使用全波傅式算法实现,每周波采样24个点。
动作区间:[-0.06N, 0.08N];可靠系数=1.75;0=1ms。
图3给出了系统振荡状态下侧os的变化特性,os在振荡时呈现余弦特性的规律性变化。图中发现按照式(1)计算的os在功角等于0°附近时,会从1突变到-1经过动作区间,但是此时计算的2考虑了一定的裕度,实际停留时间1仍将小于3,判据不会误开放。

图3 振荡状态下Uos的变化特性
表2给出了不同振荡周期下os进入动作区域内的速度、理论计算时间和实际停留时间。结果表明,系统振荡时新判据不会开放,保护不会误动作,判据具有可靠性。

表2 振荡条件下判据计算结果
当系统振荡中发生对称性故障时,os的变化特性、新判据中os在设定区间内预测计算时间3和实际停留时间1的关系如图4所示。仿真中,振荡周期为300ms,故障持续时间为300ms。由图4可知,当振荡时,实际停留时间1小于计算时间3,判据不开放;当振荡时发生对称性故障时,os快速稳定在区间[-0.06N, 0.08N]内,计算得到的时间3为11.8ms。由图可知,实际os进入区间[-0.06N, 0.08N]内停留11.8ms后,就满足开放条件。新判据在满足条件11.8ms后就可开放保护动作,新判据动作速度快。
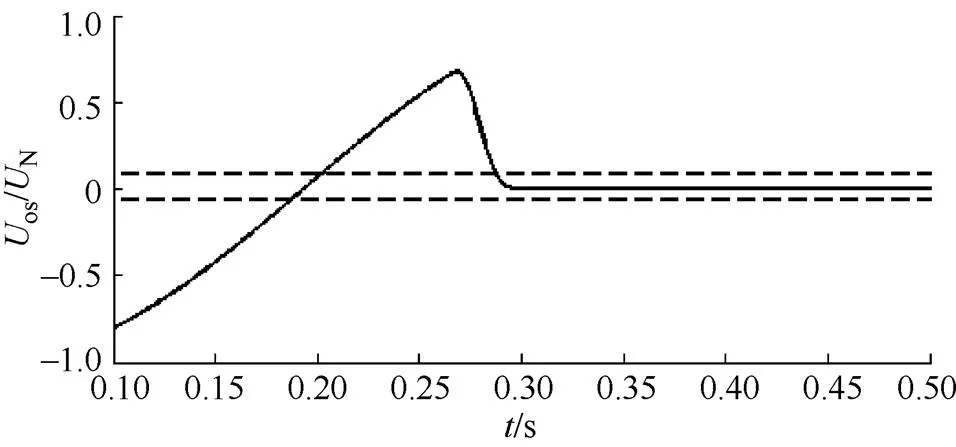
(a)os计算结果
(b)测量时间1与计算时间2
图4 振荡周期=300ms,发生对称性故障
在振荡周期为1500ms时,如图5所示,新判据同样很快就满足条件,经延时14.3ms后即可开放保护动作。

(a)os计算结果
(b)测量时间1与计算时间3
图5 振荡周期=1500ms三相故障时的仿真结果
系统运行条件与上述相同,振荡周期为300ms,故障持续时间为300ms,在系统两侧发生功角摆至 180°时发生了三相接地故障。若故障前os就已经进入动作区间,则计算时间3为的振荡条件下计算的时间。在此种情况下,判据延时最长,如图6所示,在满足条件21.7ms时才能开放保护。统计资料表明,振荡过程中振荡周期最短为0.1~0.15s,个别的约为0.08s,在系统恢复同步前最后一个振荡周期最长,一般可按3s考虑[10]。在最极端情况下,考虑在振荡周期3s时发生此类故障,按照表2中数据,判据需要在满足条件179.2ms后才能开放保护,此时间长于固定延时150ms的时间。

(a)os计算结果
(b)测量时间1与计算时间2
图6=300ms,=180°时发生三相故障的仿真结果
在正常运行时,os一直保持在较高值。若此时发生扰动,再经160ms后发生三相故障,则os快速跌落到动作区间内,如图7所示。由判据动作情况可知,满足条件11ms后就可以开放保护,与固定延时150ms相比,新判据动作迅速。

(a)os计算结果
(b)测量时间1与计算时间3
图7 正常运行发生三相故障时的仿真结果
4 结论
本文提出了一种基于振荡中心电压的三相故障开放判据,发生故障时,开放时间根据故障时的系统的功角所确定。故障前功角越小,计算电压os越大,其值跌落速度越快,判据开放所需延时越小。与传统固定延时相比,新判据提高了保护的动作速度。尤其在不改变现有的振荡闭锁配置情况下,加快了正常运行的系统在受到扰动后经短时开放160ms之后又发生区内故障时保护的开放动作速度。此外,该判据具有自适应,易于整定,易于实现。仿真结果证明了该判据的正确性和有效性。
[1] 张保会, 尹项根. 电力系统继电保护原理[M]. 北京: 中国电力出版社, 2005.
[2] 国家电力调度中心. 继电保护培训材料[M]. 北京: 中国电力出版社, 2009.
[3] 江清楷, 黄少锋, 杨琳, 等. 电力系统振荡对三相故障距离继电器影响的分析及对策[J]. 电力自动化设备, 2012, 32(2): 85-88, 94.
[4] 邓华, 高鹏, 王建全. 关于振荡角的振荡中心电压和cos的变化特征[J]. 电力系统及其自动化学报, 2007, 19(1): 68-73.
[5] 高鹏, 王建全, 周文平, 等. 关于振荡中心的研究[J]. 电力系统及其自动化学报, 2005, 17(2): 48-53.
[6] 沈国荣, 邓绍龙, 朱声石. 区分振荡与短路的新原理[J]. 电力系统自动化, 1990(1): 7-12.
[7] Kase T, Sonobe Y. A New Method for Fault Detection during Power Swing in Distance Protection[J]. IEEE Trans. Power Delivery, 2005: 108-111.
[8] 刘凯, 索南加乐. 基于线路两端电压间夹角的三相故障开放判据[J]. 电力系统自动化, 2010(7): 66-69.
[9] 邵震宇, 田伟, 鲁雅斌. 一种振荡中对称性故障的快速识别方法[J]. 电力系统保护与控制, 2011, 39(22): 68-71.
[10] 赵志华, 张红跃, 易永辉. 一种在振荡闭锁期间发生故障时快速开放距离保护的方法[J]. 继电器, 1997(1): 18-21.
[11] 黄少锋, 赵远, 申洪明, 等. 一种基于功角计算的振荡闭锁方案[J]. 电力系统自动化, 2015(1): 87-91.
[12] 鲁文军, 林湘宁, 黄小波, 等. 一种采用浮动门槛的自适应突变量距离保护方案[J]. 电工技术学报, 2009, 24(6): 160-165.
[13] 李振兴, 尹项根, 张哲, 等. 基于序电流相位比较和幅值比较的广域后备保护方法[J]. 电工技术学报, 2013, 28(1): 242-250.
[14] 郭振威, 姚建刚, 康童, 等. 一种输电线路超高速方向保护方法[J]. 电工技术学报, 2016, 31(22): 168-177.
[15] 马燕, 唐仁权, 朱海清, 等. 基于突变量的光纤比相差动保护原理及实现[J]. 电气技术, 2014, 15(8): 56- 59.
[16] 张兆云, 陈卫, 张哲, 等. 一种广域差动保护实现方法[J]. 电工技术学报, 2014, 29(2): 297-303.
[17] 李波, 邢素娟, 莫杰锋, 等. 基于光纤通道的双端保护联调[J]. 电气技术, 2015, 16(1): 110-112.
[18] 隋凤海, 李钢, 王善祥, 等. 余弦电压元件的特性及其应用[J]. 电力系统自动化, 1997(5): 29-31.
New Power Swing Unblocking Criterion of Symmetrical Fault for Line Protection Relay based on Oscillation Center Voltage
Li Bin1Zheng Yuping2Chen Ruijun1
(1 State Grid Jiangsu Electric Power Company, Nanjing 210003; 2. NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing 210003)
A new Power Swing Unblocking Criterion of Symmetrical Fault for line Protection Relay is presented in this paper. The defined calculated voltage is equal to the voltage at the swing center during power swing, while it keeps less than arc voltage when a Symmetrical Fault is occurring. What is more, The defined calculated voltage can be considered as uniform changing in a short range, which makes the stay time of calculated voltage in the range can be calculated. According to these characters, An adaptive power swing unblocking criterion is presented. The new criterion is easy to use in current relay protection.
power swing; unblocking criterion; symmetrical fault; cosin function; adaptive
李 斌(1991-),男,助理工程师,主要研究方向为电力系统继电保护。

