磁力轴承用两电平数字开关功放仿真与实验研究

张 柯, 刘明学



磁力轴承用两电平数字开关功放仿真与实验研究

张 柯, 刘明学

（武汉船用电力推进装置研究所，武汉430064）

本文阐述了磁力轴承用两电平数字开关功放的实现原理，从理论上分析了数字功放的评价指标电流响应速度与电流纹波，考虑开关管、二极管特性等非线性因素，推导了电流纹波的理论表达式；考虑AD量化过程，建立了基于Simulink的仿真模型，并进行了仿真；搭建了数字功放实验平台，进行了不同工况下的实验研究。结论表明，仿真模型与实际功放的带宽比较接近，电流纹波的理论值、仿真值、实验测试值较为接近。

数字功放 电流纹波 电流响应速度

0 引言

磁力轴承具备无机械接触、无摩擦、无需润滑、支承特性可控等突出优点，是高速精密转子的理想支承，具有广阔的应用前景[1]。功率放大器是磁力轴承控制系统中的核心部件，其作用是在电磁线圈中产生精确的受控电流以产生维持转子系统正常工作的电磁力，其性能直接影响转子系统的动态特性。

开关功放由于控制驱动简单、易实现和能量转换率高等优点，是目前磁力轴承控制系统中实现能量转换的主要方式。西安交通大学的陈立群等人在分析磁力轴承性能要求的基础上，从开关效率及频率、器件选择、电流响应率、算法设计和噪声等方面入手，针对开关功放进行了样机研制和实验研究，完善了开关功放的设计准则[2]。

开关功放按照运算方式，可分为模拟功放和数字功放，数字功放由于算法设计灵活，驱动波形生成简单，是开关功放的主要发展趋势。

在分析磁力轴承系统时，一般将数字功放等效为一阶惯性环节来分析，采用简化模型，虽然方便了分析整个控制系统，但是由于数字功放中含有数字控制器、开关管和二极管等非线性单元，其具有很强的非线性，因此将数字功放模型简化为一阶惯性环节很难保证模型的精度，所以需建立精确的开关功率放大器数学模型。文献[3]建立了PWM开关功率放大器的谐波模型，但仅考虑基波，缺乏输出电流的精确数学表达。文献[4]建立非线性模型的电路状态空间，可得磁悬浮轴承功率放大器的模型，但仅能分析直流稳态特性。文献[5]基于谐波平衡原理，采用了傅里叶变换，对负载两端电压进行了分解，建立了两态和三态调制功放的线性化谐波模型，能较准确的描述开关功率放大器的输出特性。文献[6]基于Simulink软件建立功率放大器电路模型，由软件内部的子模型库搭建，通过选择电路特定的器件子模型，而不需要建立电路的数学模型即可仿真。目前对开关功放的仿真多是针对其纹波特性的仿真，不具有实际物理意义，对于功放的PI参数设计指导意义不大。本文采用Simulink电力电子库中元件搭建具有实际物理意义的仿真模型，考虑了器件本身的参数，并进行了实验验证。

1 数字功放的实现原理

两电平数字功放的半桥控制原理图如图1所示，主要由DSP系统、驱动电路、半桥转换电路及反馈回路组成。数字功放根据控制器的给定电流指令，通过半桥主电路转换成线圈电流，其本质为跟踪控制系统。

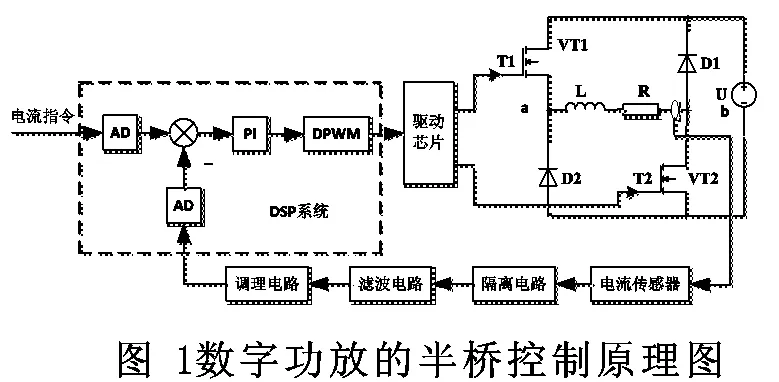
DSP系统采用将电流指令信号与电流反馈信号离散成数字信号并做差，差值作为数字PI的输入，进而确定数字PWM（DPWM）的占空比，生成所需占空比的DPWM信号，通过驱动电路驱动半桥电路的上下桥臂，在线圈中产生所需的电流。

DPWM信号是由占空比数值与基于计数器的三角载波交截生成，图2为单极性上升沿改变的DPWM生成原理图。忽略的导通压降，线圈两端电压有两种状态。当占空比Δ<50%时，线圈两端电压负电压时间大于正电压时间，在单位DPWM周期内电流减小；当占空比Δ=50%时，线圈两端电压负电压时间等于正电压时间，在单位DPWM周期内线圈电流不改变；当占空比Δ>50%时，线圈两端电压负电压时间小于正电压时间，在单位DPWM周期内线圈电流增加。

一般DSP系统生成的DPWM信号只提供逻辑电平，输出电压和输出电流很小，无法驱动开关管，保障其正常工作，此外，加在开关管两端的电源通常要远远大于数字芯片的供电电源，为了保护数字芯片，通常在功率桥路控制端增加一级隔离电路：一是为了在不改变数字芯片输出DPWM信号逻辑电平的条件下，增强PWM的驱动能力，保障开关管能够工作正常；二是隔离控制器和功率桥电路，提高系统的抗干扰能力。

功放的反馈回路是保障功放稳定性的基础，但是电流信号不能够直接被采集，通常通过电流传感器进行比例衰减，再经过采样电阻转换成电压信号，经过隔离、滤波、调理等电路转换成与参考信号同一级别的电压信号。理想的反馈能够无误差地反映电流的变化趋势，但是在增加的每一级环节都有可能引入新的误差与延迟，导致功放输出电流的精度变低、响应速度变慢，所以必须合理设计反馈回路中各环节以降低反馈误差、减小延迟，提高系统的控制精度。

2 两电平数字功放的评价指标

评价功放性能的主要指标有：电流响应速度、输出电流纹波。下面对此进行一一分析。

磁力轴承功率放大器的输出与电磁线圈相连，因此其负载主要呈感性，输入信号的幅值将对功放的幅频响应和相频响应等动态特性产生显著影响。评估功放特性的重要参数之一是功放的电流响应速度，在电路参数不变的前提下，母线电源对线圈进行充电时功放的电流响应速度达到最大值：

上式中为功放母线电压，为开关管管压降，为磁力轴承线圈电感，为磁力轴承线圈电阻，为磁力轴承线圈电流。由于线圈电阻一般为几欧姆，开关管压降一般为几伏，因此忽略线圈电阻和开关管压降后可得简化后的电流响应速度表达式：

两电平调制方式下，功放在跟踪固定电压信号时，输出电流平均值固定不变。线圈两端电压为固定值时，流过的电流成指数特性变化，而在一个开关周期内，电流变化很小，可以将电流变化率近似为固定值，即成线性变化。假设电流从a到b，两电平策略下，开关功放输出电流变化曲线图如图3所示。

在一个开关周期内，流过线圈的电流与母线电压之间的关系可以表示为：

式中U为续流二极管导通压降。由于一个开关周期内电流的变化量相对于电流平均值很小，电阻上的电压变化值很小，可以用代替。电流变化率用直线近似后，上式可以简化为

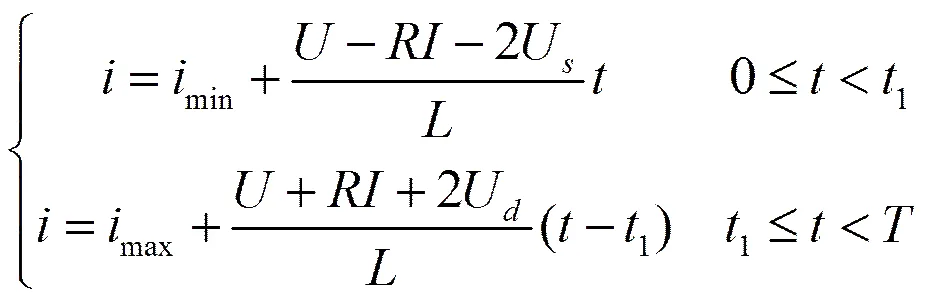
由于电流在一个开关周期内为连续变化，所以

由上式可得

因此电流纹波的表达式为

通过以上分析可知，两电平功放的纹波大小与静态工作电流、母线电压、线圈参数、开关管以及续流二极管的性能参数密切相关。当功放跟踪固定信号时，电流纹波与开关管的工作频率成反比，与线圈电感成反比。但是当磁力轴承设计完成后，线圈参数就已经确定。一般而言，不同开关管之间的导通压降、导通内阻区别不大，续流二极管的导通压降比较固定。为了降低功放纹波电流大小，只能通过增大开关频率或者减小母线电压来实现，但是选用高开关频率的开关管来满足性能要求势必增加硬件成本，而减小母线电压必然会降低系统的动态特性，所以很难采用两电平策略来设计高精度、高响应的功放。

3 数字功放的仿真模型

根据图1，在Simulink软件中搭建数字功放的仿真模型，如图4所示。选用IGBT、二极管Diode及线圈Coil等模块搭建功率转换电路。数字功放中DSP系统信号处理过程为采样-运算-输出，所以选用零阶保持器Zero-Order Hold模块和增益模块模拟量化过程，数字PI模块PI（Z）作为主要运算方法，因DSP芯片的信号输出存在固定延迟，增加延迟环节以保证仿真模型的准确性；PWM Generator和增益模块生成所需PWM波；因实际设计反馈回路时，必须保证电流反馈信号速度远远高于处理器速度，可以认为反馈回路可以无误差跟踪实际电流，所以选用增益模块作为反馈回路传递函数。

设定数字功放的主要参数，见表1。

根据表1中数据，可知反馈回路增益为1；AD位数为10位，因此最大电流1A对应的数值量为1024，即AD量化增益为1024；PI运算输出的数值D(Z)所对应的占空比为D(Z)7500。

4 数字功放实验平台与实验结果分析

搭建的实验平台如图5所示，使用的仪器设备包括：工控机、仿真器、电流控制器、功率桥、信号发生器、母线电压、示波器。

为了验证数字功放仿真模型的正确性和准确性，实验中数字功放的参数均与仿真环境一致。图6为数字功放的1A阶跃响应仿真与实验对比图，电源电压50 V，为4.16，为11.40 krad/s。

电流响应速度一般通过带宽来反映，而控制系统的带宽可以通过幅频响应图来获得。仿真环境下进行数字功放的幅频响应实验，幅频响应图见图7，由图可知在该参数下，数字功放的带宽为2.03 kHz。

实验环境下，输入峰峰值为1 A正弦信号，改变输入信号频率，测量输出信号的峰峰值，当输入信号频率为1.92 kHz时，输出信号峰峰值为输入信号的0.707倍，如图8所示，可知数字功放的带宽为1.92 kHz。对比仿真环境，数字功放的带宽误差为5.73%，可知仿真模型能够较好地反映数字功放的带宽。下面将对数字功放仿真模型的纹波特性进行验证，表2、3分别为不同开关频率、母线电压下，数字功放电流纹波的理论值、仿真实验值、实验测量值，并分别绘制电流纹波与开关频率、母线电压的关系曲线图，如图9、10所示。

由图9、10可知，电流纹波的理论值、仿真实验值、实验测量值比较接近，且随开关频率、母线电压的变化趋势一致，可以证明本文建立的数字功放模型能够反映出实际功放的纹波特性。

图9 输出1A时，四种开关频率下电流纹波对比图

5 结论

阐述了数字功放的实现原理，分析了数字功放的评价指标，推导了数字功放电流纹波的表达式，考虑AD量化过程、IGBT的导通压降及二极管的导通压降，在Simulink环境中搭建了两电平数字功放仿真模型，该模型能够反映实际功放的输出特性。

搭建了数字功放实验平台，针对数字功放的电流响应特性与纹波特性进行了仿真与实验研究，理论、仿真与实验三者电流纹波值相近，电流纹波随母线电压及开关频率的变化趋势一致；在相同参数下，仿真与实验的带宽接近；证明本文所采用的模型可用于指导功率放大器设计。

图10 输出1A时，四种母线电压下电流纹波对比图

[1] 冯锐，郑世强，房建成. 高速磁悬浮电动机对拖试验中转子不量在线辨识与振动控制[J]. 机械工程学报，2014，50(3):71-77.

[2] 陈立群,谢友柏. 电磁轴承开关功放设计[J]. 机电工程,1998,02:51-53.

[3] 张亮, 房建成. 电磁轴承开关功放的谐波模型仿真与实验研究[J]. 中国电机工程学报，2007，27(21):95-100.

[4] Wang Jun, Xu Longxiang. System model of three-level switching power amplifier for magnetic bearing[C].ICMTMA,Zhangjiajie, 2009.

[5] 王军, 徐龙祥. 磁悬浮轴承开关功率放大器等效数学模型[J]. 电工技术学报，2010，25(4):53-58,64.

[6] 张亮, 房建成. 电磁轴承开关功放的谐波模型仿真与实验研究[J]. 中国电机工程学报，2007，27(21):95-100.

Simulation and Verification of Two-level Digital Switching Power Amplifier for Magnetic Levitation Bearing

Zhang Ke，Liu Mingxue

(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)

This paper describes the principle of two-level digital switching amplifier for magnetic bearings, and theoretically analyzes the current response speed and current ripple of digital amplifier. Considering nonlinear factor switch and diode characteristics, the theoretical expressions of current ripple are derived, the simulation model is established based on Simulink considering AD quantization, and the experimental platform of digital amplifier is built for experimental research in different conditions. The conclusions show that the bandwidth of simulation model is close to the actual amplifier, and the current ripple is also close among the experimental values, the simulated values and the theoretical values.

digital power amplifier; current ripple; current response speed

TN721

A

1003-4862（2017）01-0052-05

2016-08-15

张柯（1990-），男，硕士，助理工程师。研究方向：磁悬浮控制技术。Email:zh_ker@126.com