基于Max-Log更新的马尔科夫链蒙特卡洛MIMO检测增强算法

胡剑浩，周将运，何帅宁，陈杰男



基于Max-Log更新的马尔科夫链蒙特卡洛MIMO检测增强算法

胡剑浩，周将运，何帅宁，陈杰男

(电子科技大学通信抗干扰国家级重点实验室 成都 611731)

针对传统的马尔科夫链蒙特卡洛(MCMC)算法，提出了一种基于Max-Log更新的MCMC-MIMO检测算法。该算法采用了基于Max-Log更新的采样，可以有效产生收敛于后验概率(APP)分布的比特样本列表集合，同时可避免计算传统MCMC算法中的每比特概率分布。但是该检测算法在高信噪比下，采样过程会陷入锁死到局部最优态。在此基础上，提出了3个增强技术：1) 抖动处理，对给定置信区间内的更新进行抖动处理；2) 条件下重新初始化，对处在潜在锁死态的采样序列进行重新初始化；3) 修剪饱和处理，利用球形译码算法中的修剪饱和技术来处理MIMO检测输出的对数似然信息(LLR)。仿真结果显示，基于Max-Log更新的MCMC增强算法能有效地解决陷入锁死的问题，从而提高系统性能并降低系统的计算复杂度。在复杂度为MMSE-PIC检测算法的90%的基础上，性能提高了2 dB。

抖动处理; 修剪饱和; Max-Log更新; MCMC; 条件下重新初始化

MIMO技术能有效地提高系统容量和频谱效率，已经被3GPP LTE/LTE-Advanced和IEEE 802.16e/ 802.16m WiMax等无线协议采纳。基于软输入软输出(soft input soft output，SISO)模型的迭代检测译码被认为能够逼近MIMO信道的香农限[1]，因此学术界和工业界提出了多种迭代检测算法。文献[2]提出了基于MMSE- PIC(parallel interference cancellation)的线性检测算法，该算法利用译码器的外信息计算输入的软符号值，进行干扰消除，最后利用MMSE进行均衡处理。由于MMSE-PIC算法需要计算矩阵乘法和求逆，其实现复杂度依然较高且性能相对较差。LSD(list sphere decoder)算法[1]利用树搜索中的深度优先搜索产生一个列表集合来计算对数似然信息，但是LSD算法随着信道和噪声干扰的不同存在着不同的算法复杂度。文献[3]中的STS(single tree search)算法在优化LSD性能的同时降低了复杂度，每个节点最多被访问一次，但是STS算法依然采用深度优先搜索，存在着可变的复杂度和吞吐率。FSD(fixed sphere decoder)算法[4]利用宽度优先搜索产生列表集合，其计算复杂度固定，但是FSD算法很难得到软输出似然值。且由于LSD、STS和FSD算法都是基于树搜索，需要对信道矩阵进行QR分解，进一步增加了检测复杂度。

文献[5-11]提出了基于马尔科夫链蒙特卡洛模型的MIMO检测算法并进行了高速VLSI实现[11]，该算法利用蒙特卡洛积分简化LLR的计算，其中符号样本序列(或者比特样本序列)通过Gibbs采样得到。传统的MCMC检测算法具有如下优势：1) 复杂度低。由于Gibbs采样是一种随机搜索样本序列的方法，使得该算法复杂度只与样本集合大小有关，且不随发射天线数和调制阶数呈指数增长。2) 收敛速度快。利用Gibbs采样可以使得MCMC的接受率等于1，能够提高马氏链的跳转效率和收敛速度。3) 可并行处理。Gibbs更新过程和LLR的计算都可以并行处理。传统MCMC算法也存在如下问题：1) Gibbs采样过程是基于概率域的逐比特(逐符号)更新，需要计算每比特(每符号)的概率，然后根据概率分布进行采样更新，该过程涉及到非线性指数运算，复杂度较高。2) Gibbs采样在高信噪比(SNR)会陷入“锁死”到一个局部最优态[5-6,9]，使得采样的状态数减少，从而导致计算LLR时出现较大的误差。目前，针对问题2)，文献[5-6]提出增大温度系数(temperature factor)和增加并行度的方法，但是仿真表明这两个技术只能降低陷入锁死的概率，而不能从根本上解决“锁死”问题；文献[9]利用ZF、MMSE进行预处理，增加了运算复杂度，并且无法在高SNR下消除误码平层[8]；在此基础上，文献[8]从根本上分析了进入“锁死”状态的原因，并且给出C-MCMC(constraint MCMC)的解决技术，但是C-MCMC需要自适应地选择ZF或SD作为预处理，增加了系统的复杂度。

本文提出了一种基于Max-Log更新的马尔科夫链蒙特卡洛MIMO检测算法。其原理是利用Max-Log采样获得样本列表集合，然后利用该列表集合计算LLR。该采样更新过程直接在对数域进行，因而不必计算传统MCMC算法中的概率分布，从而避免了非线性指数计算，降低了计算复杂度，有效地解决了问题1)。但是，基于Max-Log更新的MCMC-MIMO检测算法同样面临“死锁”问题，导致在高SNR出现误码平层。针对该问题本文还提出3个增强技术：1) 抖动处理技术，对置信度为50%的置信区间内的比特更新采用随机更新的方式，该技术可为马氏链提供一定的可能性跳出局部最优态，从而保证马氏链在较长的转移时间内不陷入锁死到局部最优态。2) 重新初始化技术，一旦发现马氏链陷入锁死到局部最优态，就立即启动该技术，以全新的初始态进行状态转移。3) 修剪饱和处理技术，利用球形译码算法中的修剪饱和技术处理MIMO检测输出的对数似然信息(LLR)，避免译码器因过大LLR值而无法正常工作于纠错状态，该技术一方面可以提升译码性能，另一方面也为后续的迭代检测提供更加正确的先验信息，从而帮助Gibbs采样器采得更有效的样本。上述3个技术可以在不增加硬件开销的基础上从根本上解决陷入锁死问题，在有限迭代采样周期内搜索到更多欧氏距离较小的样本，从而得到更加精确的LLR估计值，提升检测性能。结果表明，基于Max-Log更新的MCMC-MIMO检测增强算法在复杂度为MMSE-PIC检测算法的90%的基础上，性能提高了2 dB。

1 系统模型

图1给出了空间复用MIMO迭代检测的系统模型，其中发射天线数为，接收天线数为，且有。相应的频域MIMO系统模型为：

接收端采用了迭代检测译码算法，主要由SISO检测器和信道译码器模块构成。首先，SISO检测器利用接受向量和先验信息得到似然信息，在似然信息中减去先验信息后作为外信息，即有。检测器的外信息经过解交织后作为信道译码器的先验信息，译码输出的似然信息减去先验信息得到译码器外信息，即有。译码器的外信息经过交织后作为检测器的先验信息。

SISO检测器利用式(2)计算每比特的对数似然信息：

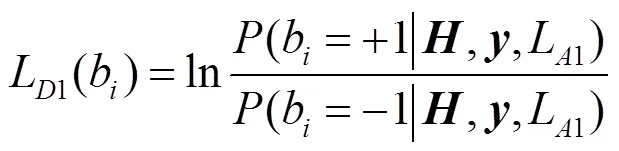
利用边缘概率函数定义可知：

(3)

因此，式(2)的每比特似然信息可以表示为：

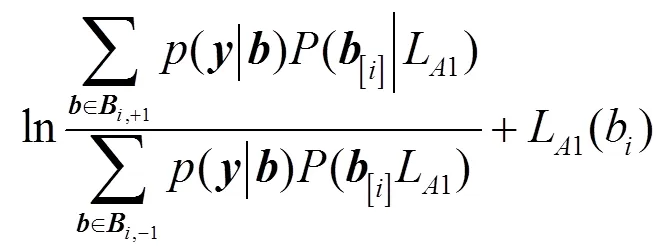
利用MAX-LOG-MAP算法[1]，式(6)可简化为：

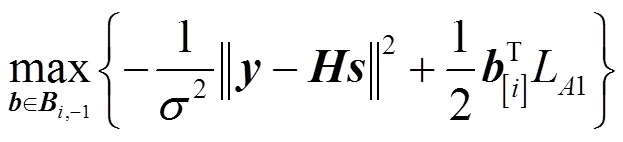
从式(7)(或者式(6))可以看出，计算每比特的外信息需要评估个比特向量，其复杂度随着调制阶数和发射天线数呈指数增长。因此，需要解决如何在避免这种穷举搜索的同时得到较好性能的问题。

2 基于Max-Log更新的MCMC迭代检测算法

为了降低式(7)计算LLR的复杂度，本文利用基于Max-Log更新的采样得到服从式(3)右端分布的比特向量列表，该列表能以极大概率包含式(7)右端的两项，分别被定义为和。和LSD类似，LLR的计算可以表示为：

(8)

为了推导本文的基于Max-Log更新的采样算法，定义每比特的条件对数似然比为：

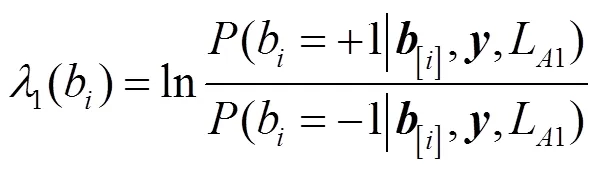
(10)

(11)

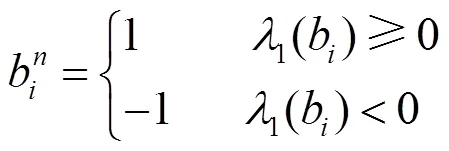
式(12)采样更新过程可概括为式(13)，即Max-Log更新的基本原理:

(13)

结合式(8)、式(11)和式(12)，得到了本文提出的MCMC整体算法，如算法1所示。

算法1 MCMC MIMO Detection based on Max-Log Updating

For=1 to

// ------------Gibbs sampler-----------------

// ------------LLR Calculator-----------------

Compute

Compute

End for;

End for;

其中计算LLR时采取了和文献[10]一样的处理，即在计算第比特的外信息时，将当前时刻采样得到的比特向量和翻转第比特的比特向量用作计算和。最后对外信息进行处理。

3 基于Max-Log更新的MCMC算法的增强技术

基于Max-Log更新的MCMC算法也存在高信噪比下陷入锁死的问题，当马氏链转移到状态时，若有：1)；2)或或，但成立，，其中表示仅改变第个比特元素后的向量，那么状态对应的条件对数比将大于，此时马氏链将长时间陷入锁死到状态，称这样的状态为局部最优态。例如，对于一个4-QAM调制的的MIMO系统，当发送比特向量为，那么便是全局最优态。假设在状态转移过程中，系统到达了一个局部最优态，即该状态对应的条件对数似然比比它的所有临近态，，，都大。此时，系统将陷入锁死到该局部最优态，使得采样的状态数减少，从而导致计算LLR时出现较大的误差。为了解决陷入锁死问题，本文提出了如下3个增强技术。

3.1 抖动处理(biased-MCMC)

基于Max-Log更新的MCMC算法类似于爬山算法(hill climbing)，其实质是一种简单的贪心搜索算法，但是会陷入锁死到局部最优态。在此基础上，本文提出了一种类似于模拟退火(simulated annealing)的抖动处理技术。将一个给定的抖动区间作为置信区间，在区间外以概率1接收更新，在区间内认为其置信水平为50%，即对于处于区间内的比特进行随机采样更新。此时，式(12)的比特更新过程变为：

该技术可为马氏链提供一定的可能性跳出局部最优态，从而保证马氏链在较长的转移时间内不陷入锁死到局部最优态。

3.2 条件下重新初始化(reinitialized-MCMC)

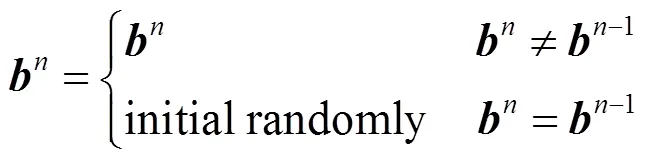
重新初始化可进一步提高系统性能，并且几乎不增加算法开销，仅仅需要一个1bit的状态标志来识别是否达到潜在锁死态。

3.3 修剪饱和处理(clipped-MCMC)

在LSD算法中，LLR-clipping技术能在复杂度和性能之间进行折中。由于较大的LLR值会使得译码器无法正常工作于纠错状态，本文将修剪饱和处理(clipping)技术运用到MCMC算法中对输出外信息进行修剪饱和处理，即：

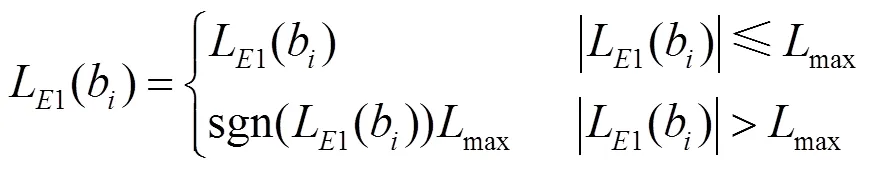
该技术一方面可以提升译码性能，另一方面也为后续的迭代检测提供更加正确的先验信息，从而帮助Gibbs采样器采得更有效的样本。

4 性能与复杂度仿真

4.1 性能仿真

本文的仿真研究都是基于128个子载波，收发天线数均为4的OFDM-MIMO系统模型，其编码器采用码率为1/2的卷积码[133 171]，调制方式为16QAM。接收端采用迭代检测译码算法，其中译码器为BCJR译码，信道模型为准静态瑞利衰落信道。

图2给出了传统MCMC算法的仿真性能，其中serial表示串行深度为50的Gibbs采样，parallel表示5路并行深度为10的Gibbs采样，表示迭代次数。从图中可以看出，虽然并行MCMC能提高系统性能，但是即在高信噪比下存在误码平层。

不同抖动区间下对基于Max-Log更新的MCMC检测算法进行了仿真，如图3所示。仿真结果显示，抖动处理能有效地解决陷入锁死问题，从而提高系统的检测性能。但是抖动区间的大小会影响MCMC算法的性能：区间太大，Gibbs采样过程跳转更剧烈，类似于随机游走，性能会降低；区间太小，采样过程会出现原地踏步，拒绝大量的跳转，同样会降低性能。从图3可以得到最佳的抖动参数为0.15。另外，从图2和图3的仿真结果对比发现，相比传统MCMC算法，最佳抖动处理后的Max-Log更新的MCMC算法可获得超过5 dB的性能增益。

经过3种增强技术处理的MCMC检测性能仿真如图4所示。仿真结果显示重新初始化在抖动处理的基础上进一步带来了1～2 dB的性能增益，修剪饱和处理在前两者的基础上继续提高了0.2 dB的性能。图4的结果还表明了第2次迭代能提高6 dB左右的性能，而后续的迭代增益较小。基于此，图5给出前两次迭代的MMSE-wPIC算法[2]，STS算法[3]和本文的MCMC增强算法的性能仿真结果。从图中可以看出，当时，相比MMSE-PIC算法，MCMC增强算法有1～2 dB的性能增益，当时，相比准MAP算法STS，MCMC增强算法在第2次迭代只有不到1 dB的性能损失。

4.2 复杂度仿真

本文利用基于FPGA面积开销的运算器数目来评估MMSE-PIC算法、传统MCMC算法和本文的MCMC增强算法的复杂度。由于STS算法的复杂度随着信道和噪声干扰的不同存在着不同的算法复杂度，且文献[14]给出其复杂度远大于线性检测器，本文并未对其进行分析。和文献[13]一样，假设比较器为单位复杂度，加法器为比较器的2倍开销，乘法器的复杂度为加法器的10倍，除法器和平方根分别为乘法器的4.5倍和3.8倍。复数乘法器的运算复杂度为4个实数乘法器和2个加法器的开销之和。此外，根据文献[13]，由于是由星座点向量构成，式中乘法、、可通过移位加(shift-add)实现。表1给出了MMSE-PIC算法、传统MCMC算法和本文的MCMC增强算法的运算复杂度，参数与系统模型参数一致，表示发射天线数，表示接收天线数，为调制阶数，为MCMC采样列表大小，最后的总体复杂度是当，，，时的运算复杂度开销。从表中可以看出，MMSE-PIC算法和MCMC算法的复杂度都只是发射天线数和调制阶数呈多项式增长。

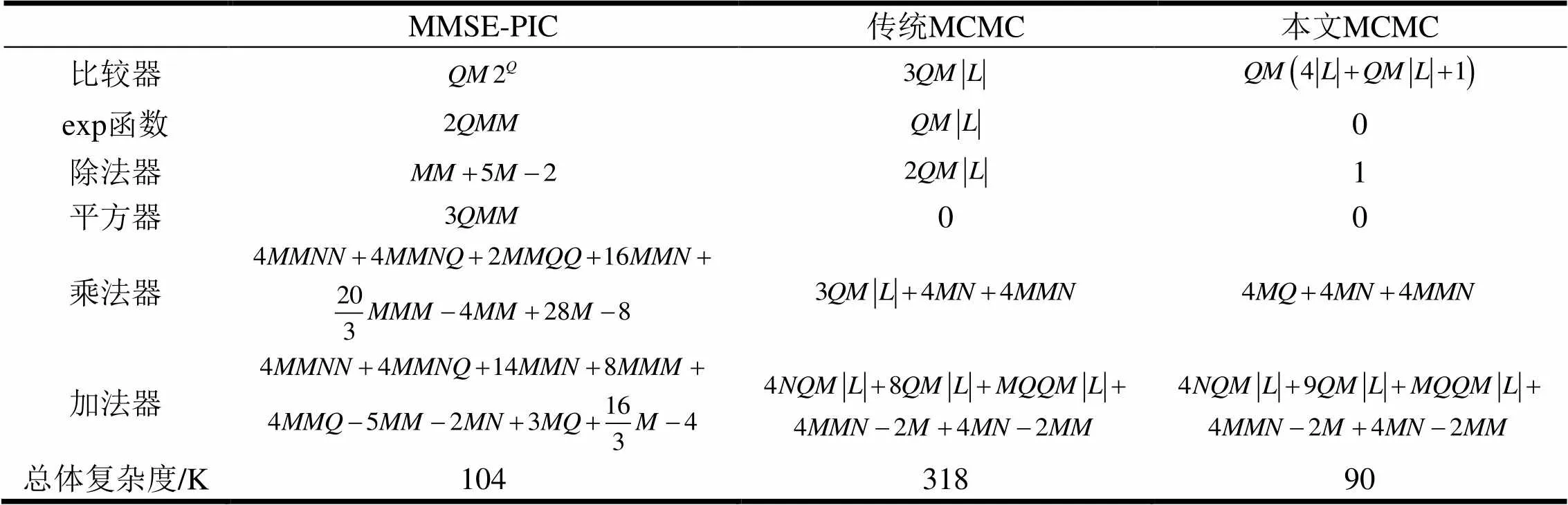
表1 MMSE-PIC和MCMC运算复杂度

5 结 束 语

本文提出了基于Max-Log更新的MCMC检测算法。该算法由Gibbs采样和LLR计算构成。首先，利用基于Max-Log更新的采样得到服从所需后验概率分布的比特向量列表，再利用MAX-LOG-MAP算法计算外信息。该MCMC检测算法具备复杂度低和可并行处理等优势，但是在高信噪比存在陷入锁死的问题，使得采样状态数减少，从而导致计算LLR时出现较大的误差。基于此，本文提出了3个增强技术：抖动处理、条件下重新初始化和修剪饱和处理。仿真结果表明：基于Max-Log更新的MCMC增强算法能有效提高系统的检测性能，并能降低计算复杂度。

[1] HOCHWALD B M, BRINK S. Achieving near-capacity on a multiple-antenna channel[J]. IEEE Transactions on Communications, 2003, 51: 389-399.

[2] STUDER C, FATEH S, SEETHALER D. ASIC implementation of soft-input soft-output MIMO detection using parallel interference cancellation[J]. IEEE Journal of Solid-State Circuits, 2011, 46: 1754-1765.

[3] ZHENG C, CHU X, MCALLISTER J, et al. Real-valued fixed-complexity sphere decoder for high dimensional QAM-MIMO systems[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4493-4499.

[4] STUDER C, BÖLCSKEI H. Soft-input soft-output single tree-search sphere decoding[J]. IEEE Transactions on Information Theory, 2010, 56: 4827-4842.

[5] FARHANG-BOROUJENY B, ZHU H D, SHI Z N. Markov chain Monte Carlo algorithms for CDMA and MIMO communication systems[J]. IEEE Transactions on Signal Processing, 2006, 54: 1896-1909.

[6] HASSIBI B, HANSEN M, DIMASKIS A G, et al. Optimized Markov chain Monte Carlo for signal detection in MIMO systems: an analysis of the stationary distribution and mixing time[J]. IEEE Transactions on Signal Processing, 2014, 62: 4436-4450.

[7] DATTA T, KUMAR N A, CHOCKALINGAM A, et al. A novel Monte-Carlo-sampling-based receiver for large-scale uplink multiuser MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2013, 62(7): 3019-3038.

[8] AKOUM S, PENG R H, CHEN R R, et al. Soft detection using constrained Markov chain Monte Carlo simulations[C]//Proceeding of IEEE International Conference on Communications. Dresden, Germany: IEEE, 2009.

[9] MAO X H, AMINI P, FARHANG-BOROUJENY B. Markov chain Monte Carlo MIMO detection methods for high signal-to-noise ratio regimes[C]//Proceeding of GlobCom. Washington, DC: [s.n.], 2007.

[10] CHEN R R, PENG R H, ASHIKHMIN A, et al. Approaching MIMO capacity using bitwise Markov chain Monte Carlo detection[J]. IEEE Transactions on Communications, 2010, 58: 423-428.

[11] DEIDERSEN U, AURAS D, ASCHEID G. A parallel VLSI architecture for markov chain Monte Carlo based MIMO detection[C]//Proceedings of the 23rd ACM International Conference on Great Lakes Symposium on VLSI. [S.l.]: ACM, 2013: 167-172.

[12] MYLLYLÄ M, ANTIKAINEN J, JUNTTI M, et L. The effect of LLR clipping to the complexity of list sphere detector algorithms[C]//Proceeding of 41st Asilomar Conference on Signals, Systems, and Computers. Pacific Grove, CA: [s.n.], 2007. 1559-1563.

[13] AMIRI K, RADOSAVLJEVIC P, CAVALLARO J R. Architecture and algorithm for a stochastic soft-output MIMO detector[C]//Proceeding of the 41st Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, [s.n.], 2007.

[14] SEETHALER D, JALDEN J, STUDER C, et al. On the complexity distribution of sphere decoding[J]. IEEE Transaction on Information Theory, 2011, 57: 5754-5768.

编 辑 税 红

An Enhanced MCMC Algorithm for MIMO Systems Based on Max-Log Updating

HU Jian-hao, ZHOU Jiang-yun, HE Shuai-ning, and CHEN Jie-nan

(National Key Lab of Science and Technology on Communications, University of Electronic Science and Technology of China Chengdu 611731)

In this paper, an enhanced Markov chain Monte Carlo (MCMC) algorithm based on max-log updating is proposed for multiple input multiple output (MIMO) system. The max-log updating can generate the list vectors to simply the complexity of the calculation of the extrinsic log-likelihood ratios (LLRs) efficiently. Meanwhile, it avoids calculating probability distribution per bit in conventional MCMC. However, the proposed MCMC detection suffers from the so called "stalling" problem, where the Markov chain may be trapped into local optimal state. Thus, we also propose three enhancement technologies: 1) biased processing, i.e., updating randomly in a given biased interval; 2) reinitialized processing, i.e., reinitialize the Markov chain under the sub-optimal states; 3) clipped processing, i.e., reprocessing the LLR with clipping. Simulation results show that the proposed algorithm can remedy the “stalling” problem efficiently with reduced complexity, and can achieve 2 dB performance gains with 10% less complexity than MMSE-PIC.

biased processing; LLR clipping; Max-Log updating; MCMC; reinitialized processing

TN92

A

10.3969/j.issn.1001-0548.2017.01.001

2015-03-23；

2015-11-20

国家自然科学基金(6150010678, 61371104)

胡剑浩(1971-)，男，博士，教授，主要从事无线通信技术和通信集成电路技术方面的研究.