导弹组合建模及电磁散射特征快速提取

何十全，王 桐，王 旭，党宏杰



导弹组合建模及电磁散射特征快速提取

何十全1，王 桐1，王 旭1，党宏杰2

(1. 电子科技大学电子工程学院 成都 610054；2. 空间目标测量重点实验室 北京海淀区 100089)

该文将常规导弹目标分解为平板、圆柱、圆台和球冠等基本几何体散射单元，通过参数化组合建模、散射场解析计算和矢量场叠加的方法，快速仿真得到导弹目标的电磁散射数据，以支持其RCS、一维距离像和二维ISAR图像等电磁散射特征提取。计算结果表明，该方法基本能够满足目标电磁散射实时、高精度计算需求，开发的仿真软件为导弹目标基于方案验证需求的电磁散射特性快速计算与评估提供了有力支持。

边缘绕射理论; ISAR图像; 组合电磁建模; 物理光学方法; 距离像; RCS

雷达目标的电磁散射特性仿真可为目标识别、武器制导和引信控制等武器装备研制与验证试验提供关键的数据支撑[1]。以导弹类目标为例，在靶场开展飞行试验之前，需获取目标的电磁散射特性数据，以检验目标是否满足考核指标要求，或为试验方案设计中的配试装备布站提供参考依据。以往的靶场飞行验证试验方案设计中，目标电磁散射特性数据主要依赖工业部门提供，或依据工程积累得到的经验公式[2]进行估算。工业部门提供的数据精度较高但计算周期较长，当目标需通过多次调整其散射特性以满足试验考核要求时，会由于计算量巨大而对试验进度造成严重影响。近年来，随着靶场飞行试验贴近实战化程度的提升，如何高效地进行目标电磁散射特性的快速估算，已成为一个亟待解决的重要课题。

众所周知，任何雷达目标散射特性的定量获取从原理上讲，最终都可归结为求解满足各种边界条件的麦克斯韦(Maxwell)方程组[3-5]的解。然而当前的仿真分析软件，无论是基于微分方程方法、积分方程方法或高频近似方法，都需要工程操作人员具有较强的电磁数理基础，以完成雷达目标的复杂几何建模和网格剖分，不利于电磁仿真软件的应用推广。同时，即使是采用高频近似方法，无论是基于面元离散[6]还是基于NUBUS曲面建模[7]，子域求和的积分策略使得电大尺寸(数十至数千波长)目标的单站散射计算仍然需要耗费一定的计算时间，导致大口径、高分辨率的一维或多维散射特征提取仍然非常困难，难以满足方案设计和论证等工程应用的实时计算需求。

针对靶场飞行试验方案设计中对导弹目标电磁散射特性的实时计算需求，本文将常规导弹目标分解为平板、圆柱、圆台(或圆锥)和椭球冠等基本几何体散射单元，首先采用物理光学方法[8]和边缘绕射理论[9]对各基本单元的电磁散射特性进行解析计算，再通过参数化组合建模、散射场解析计算和矢量场叠加的方法，快速仿真得到导弹目标的电磁散射数据。该方法可实现任意导弹类目标基于合理参数的快速组合建模与高效电磁仿真计算。无需复杂的几何建模和网格离散，设计的仿真软件可近乎实时地仿真获取导弹目标的RCS、一维距离像和二维ISAR像等电磁散射特性。

1 电磁散射高频近似

当目标的电尺寸较大时，散射变成了一种局部现象，散射体各部分之间的相互影响很小，这样就可把整个散射体作为多个独立散射单元的集合来处理。对于导弹目标，可以将其近似为平板、圆柱、圆台(或圆锥)和椭球冠等基本几何体散射单元的空间组合。因此整个弹体的电磁散射可等效为这些组合单元的电磁散射叠加。

金属目标的散射场由其表面感应电流的二次辐射引起，该散射贡献可由物理光学法近似计算。物理光学法((physical optical, PO)的数理基础是斯特拉顿—朱兰成(Stratton-Chu)散射场积分方程[10]。即由金属表面的磁场边界条件：

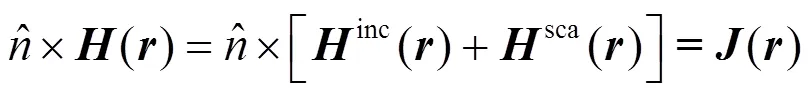
以及场-源积分表达式：

(2)

可以建立金属表面感应电流满足的磁场积分方程(MFIE)为：

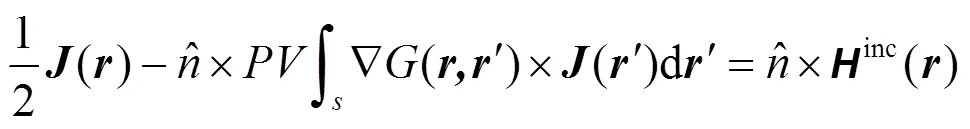
亮区 (4)

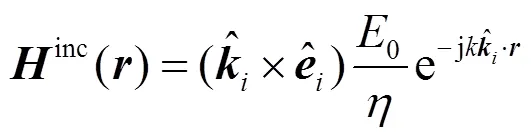
而在入射波不能直接照射的阴影区(暗区)，其他各源点耦合贡献和入射波近乎抵消，使得暗区的电流强度很小。基于此，物理光学法直接假定在物体暗区电流密度为零：

因此，由式(4)和式(6)，可根据入射场独立地近似确定目标表面感应电流分布。可见，用PO方法计算物体的散射场时，必须对物体进行面元的遮挡判别。对于关注的导弹目标，亮、暗区的判别则显得比较简单，在基本散射单元反射贡献求解和参数组合建模中再分别进行说明。

近似得到目标表面的感应电流后，由场-源积分可求解得到目标的散射场。其远区散射电磁场表达式为：

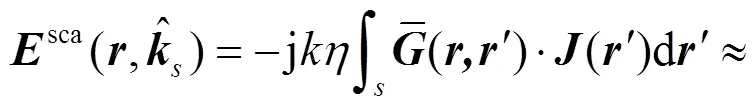
(7)

为了便于散射贡献的量化分析，可用复雷达散射截面(复RCS)[11]表示散射场的主极化分量：

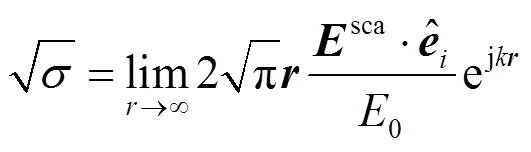
将式(7)代入式(8)，得：

(9)

式中，积分核定义为：

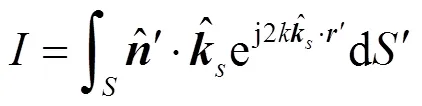
复RCS体现了散射的相位和接收机极化的影响，是一个复数量，在计算中可保持目标上各部件散射场之间的相位关系，正确地表示干涉作用。因此不同散射单元的复RCS可以直接相加，以表示不同部件总的散射效果。

目标总的RCS可以表示为：

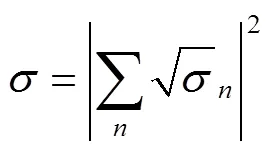
2 基本单元电磁散射贡献

由上节的分析可知，基于物理光学近似，雷达目标的散射场可由式(10)进行计算。本节对平板、圆柱、圆台和椭球等基本散射单元的积分计算进行解析公式推导。式(10)中，为散射波方向矢量，对于方向的雷达来波，单站情形的散射方向矢量可表示为：

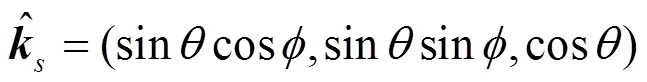
2.1 矩形平板散射

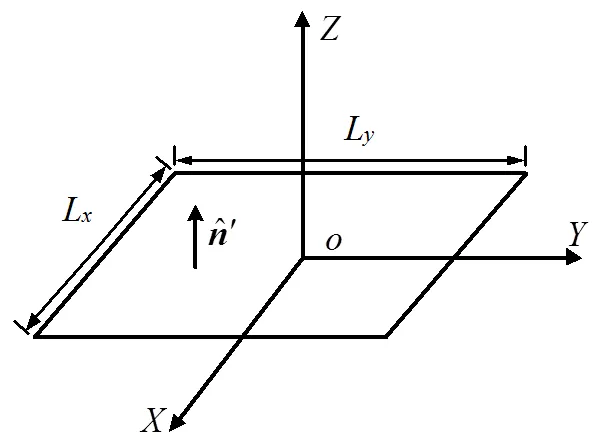
图1 矩形平板电磁计算示意图

如图1所示，平行于平面的矩形平板长和宽分别为和，平板中心位于点(0,0,)处。矩形平板上的源点和法向矢量可分别表示为：，，结合式(10)，散射积分可表示为：

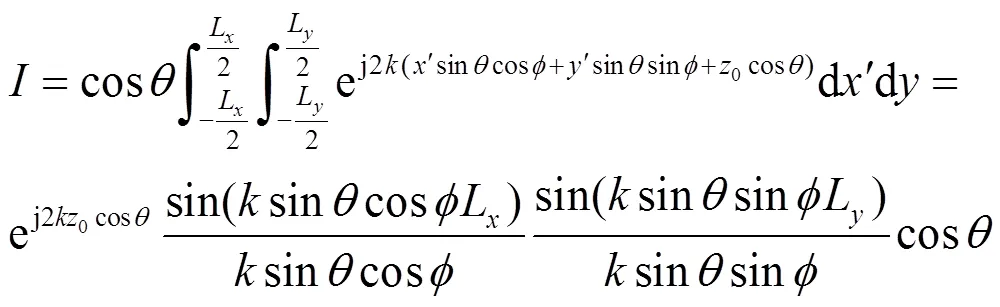
当分母为零时，可用洛必达(L'Hospital)法则[12]求极限化简式(13)，求得特殊角度时的散射结果。

2.2 圆形平板散射

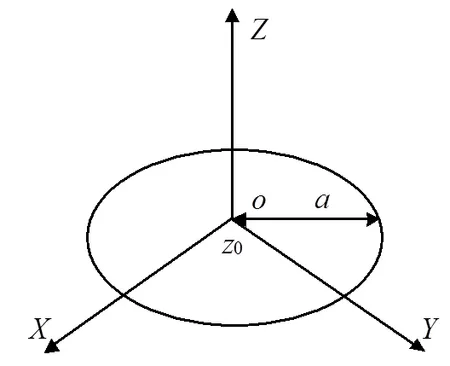
图2 圆形平板电磁计算示意图

如图2所示，平行于平面的圆形平板半径为，平板中心位于点(0,0,0)处。圆形平板上的源点和法向矢量可分别表示为，，结合式(10)，散射积分可表示为：

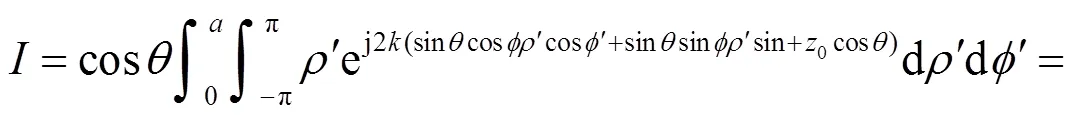
为了求取式(14)中的内层积分，利用贝塞尔函数恒等式：

(15)

将式(15)代入式(14)，得到：

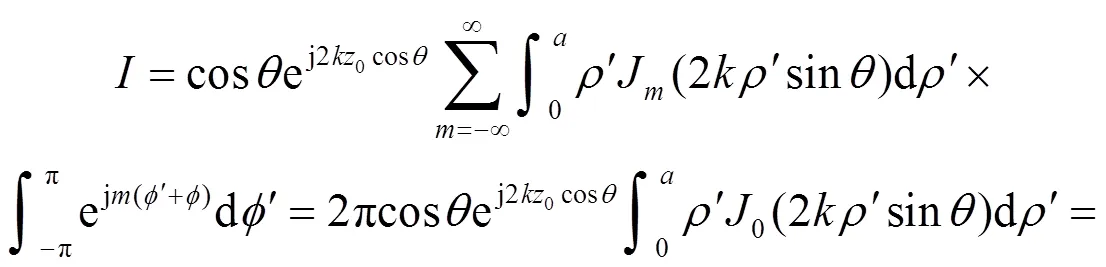
(16)

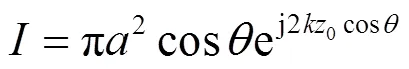
2.3 圆柱面散射

图3 圆柱面电磁计算示意图

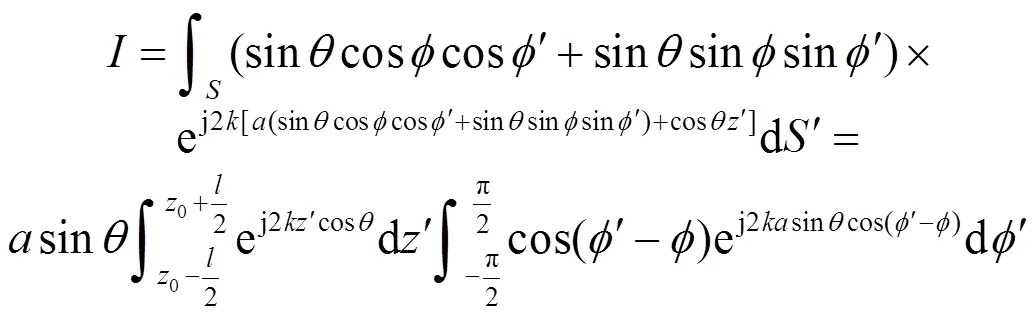
(19)

鞍点法[13]首项近似公式为：

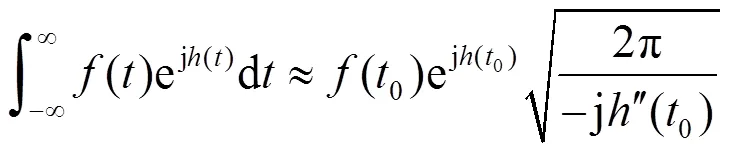
(21)

因此，式(10)可最终表达为：

(23)

2.4 圆台和圆锥面散射

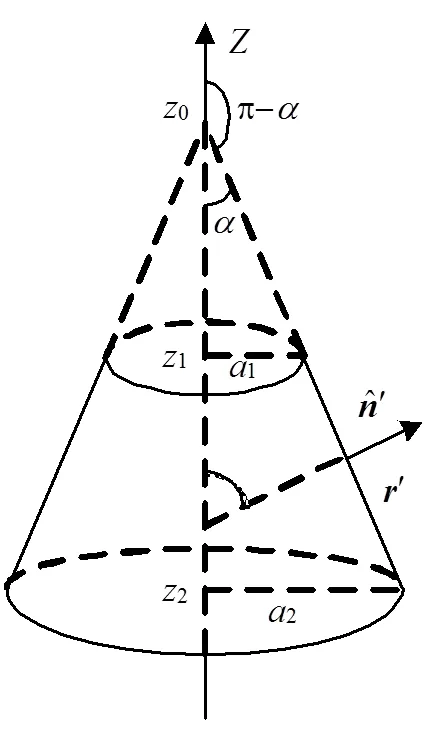
图4 圆台(锥)面电磁计算示意图

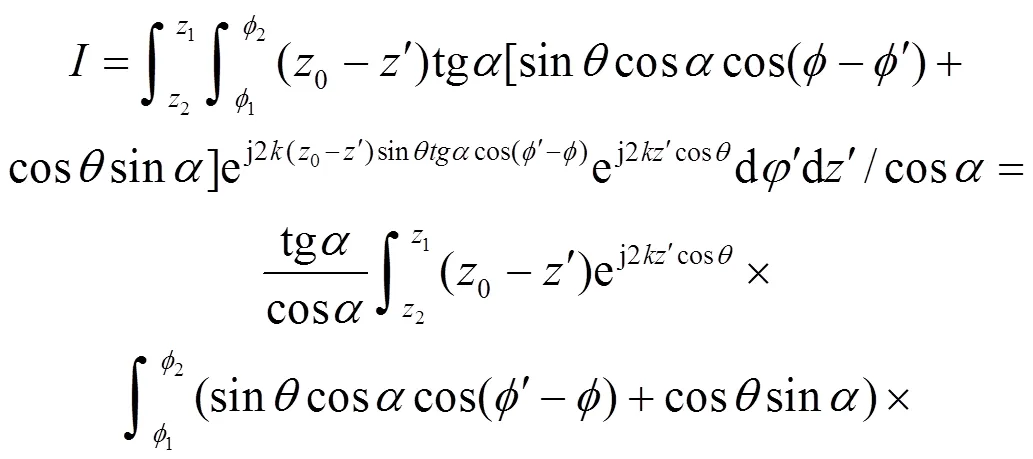
(24)

2.5 椭球冠散射

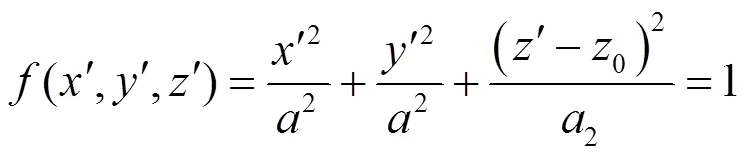
椭球面上的源点可以用球坐标变量表示为：

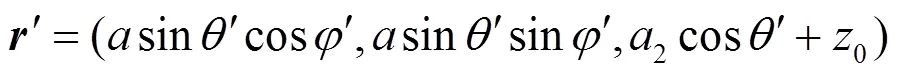
由图中几何关系有：

(27)

因椭球面上任意一点处的外法向矢量与椭球函数的梯度方向一致，处的法向矢量可表示为：

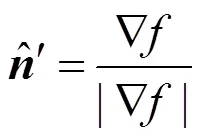
其中

(29)

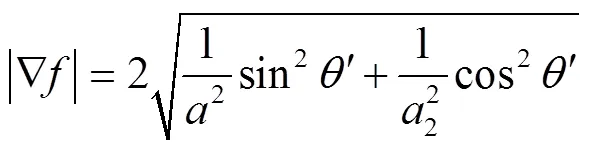
(31)

(32)

将式(31)、式(32)代入式(10)，得[15]：

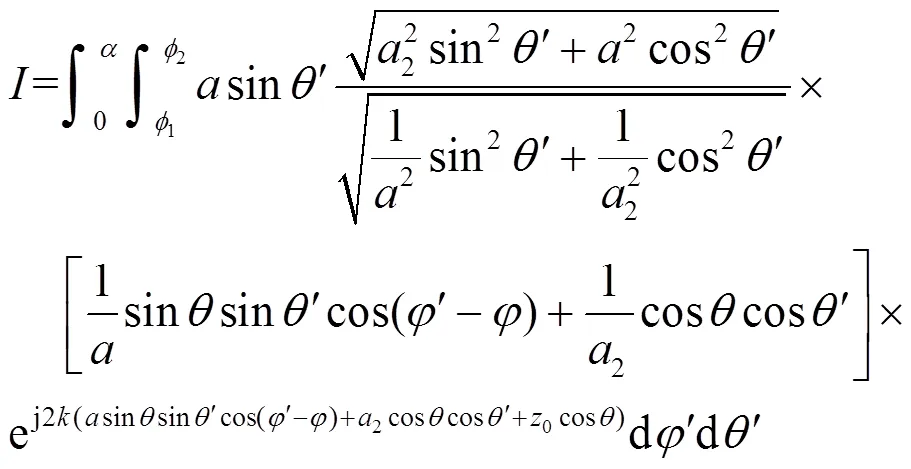
与圆台面的分区讨论和计算类似，可由鞍点法对式(33)中关于的内层积分进行化简，仅剩下关于的线积分，然后通过辛普森积分实现快速计算。

3 边缘绕射贡献

目标的高频散射主要来自于光滑曲面的镜面反射，以及表面不连续处的边缘或尖端绕射。物理光学方法能较为精确地描述光滑曲面的镜面反射贡献[16]。用平板、圆柱、圆台和椭球冠等基本散射单元组合成弹体目标时，基本单元结合处的边缘会产生绕射现象，在某些角度可能成为目标RCS的重要组成部分，需要单独考虑其贡献。

用于目标绕射分析的方法很多，常用的方法包括几何绕射理论(GTD)[17]、一致性几何绕射理论(UTD)[18]、等效边缘电磁流(EEC)法[9]、增量长度绕射系数(ILDC)[19]等，为了更好地与物理光学(PO)法进行结合，本文选择EEC法计算边缘绕射贡献。

EEC采用等效电磁流方法解决边缘绕射问题，其原理是：当任何有限电磁流分布的远区绕射场通过一个辐射积分来求和时，将得到一个有限的结果，若能找到这种适当的分布，则可避免几何绕射理论的发散问题。其基本方法是假设在环绕表面奇异性(边缘回路)的各点处存在线电流和线磁流，并用远场辐射积分的形式表示绕射场：

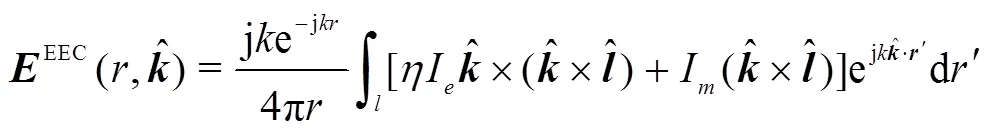
(35)

本文采用物理绕射理论-等效边缘电流法(PTD-EEC)[20]计算目标边缘绕射作用，采用三角变换的方法去除虚假奇异点[21]，再将求出的绕射贡献对物理光学法计算所得散射场进行修正，从而得到更为精确的RCS数据。

4 组合参数建模及软件实现

由第2节的分析可知，对于平板、圆柱、圆台或椭球等几何形体比较规则的散射单元，式(10)的散射积分可解析或降维表达，而无需进行网格剖分和采用费时的曲面数值积分，因此具有很高的计算效率。并且，计算时间几乎与频率(目标电尺寸)无关。工程应用时，只需要指定基本散射单元的半径、高度、中心位置等几何参数，以及雷达频率与来波方向等电磁参数，通过高频镜面散射场和边缘绕射场的参数化解析计算，然后相干叠加，就可以快速获取组合目标的电磁散射数据，实现过程方便且高效。

为了方便电磁散射特征提取和工程设计应用，本文利用MATLAB的高级图形功能[22]设计开发了基于参数化组合建模的电磁仿真软件，软件界面如图6所示。软件集参数化组合建模、电磁参数输入、电磁散射实时计算和结果显示为一体。

界面左侧为计算参数输入区域，可以设置入射波频率、俯仰角和方位角等常规RCS计算参数。也可以通过下拉菜单选择一维距离像、二维ISAR像等仿真功能。在模型组合区域可以非常方便的增加或删除基本散射单元，通过修改基本单元的模型参数，包括单元类型、上下底面位置()及半径()等，可组合生成任意导弹目标的几何外形，并且在界面右侧的模型区域实时显示。其中，基本单元类型分为圆台类(圆盘、圆柱和圆锥视为圆台的特殊情况)、椭球类和平板类；上下底面位置参数用于确定各基本单元的相对位置；上下底面半径用于确定各基本单元的尺寸大小。常规导弹目标基本可分解为各种圆台类单元的组合，结合椭球类和平板类可实现计算目标的多样性扩展。

对于组装好的弹体模型，软件可以自动进行亮暗面判断和快速地进行RCS计算与分析，其RCS计算结果以列表和图形的形式显示在界面右侧，同时以文档形式保存。

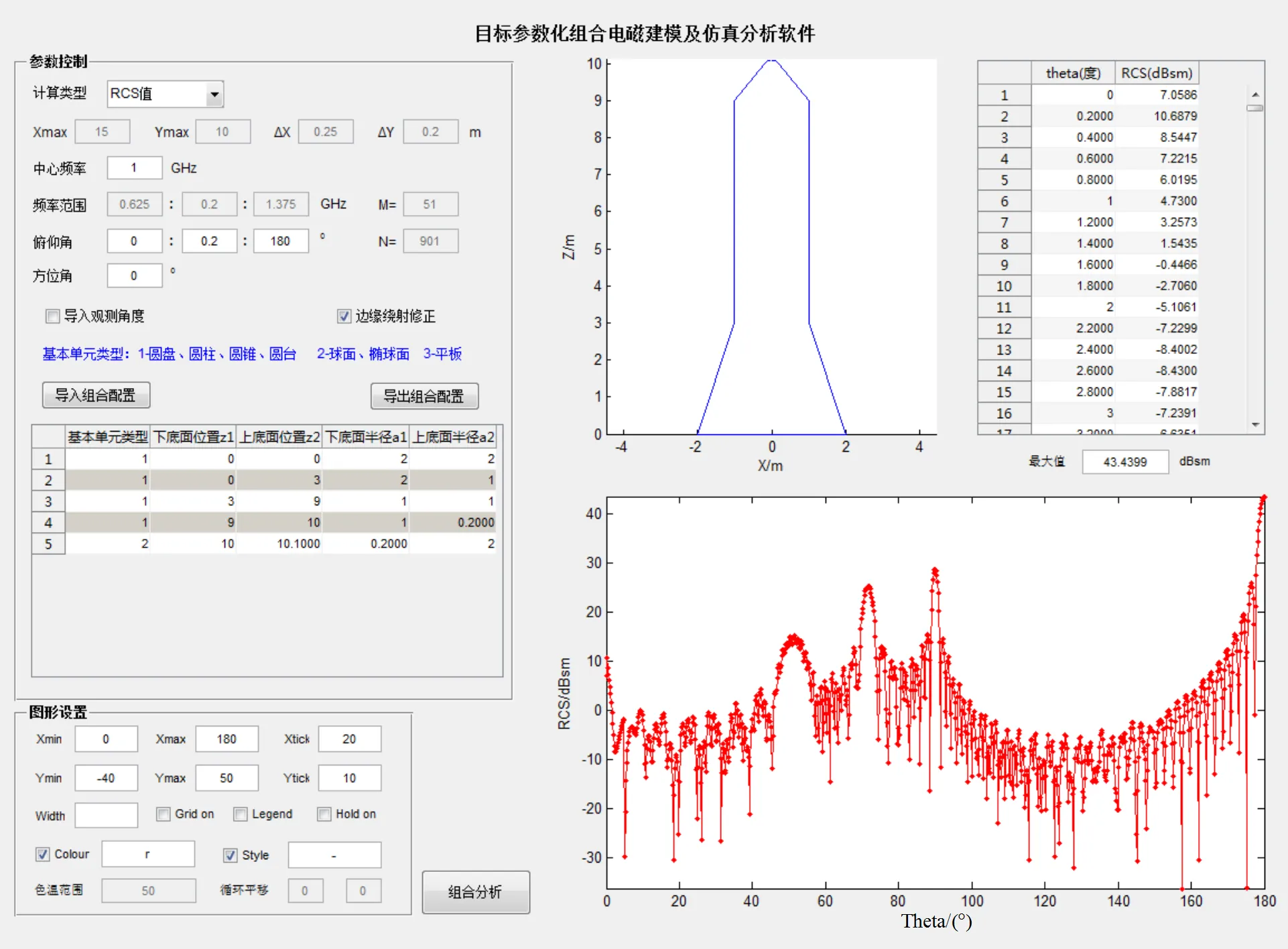
图6 目标参数化组合建模及仿真分析软件界面

5 散射特征提取及应用案例

5.1 散射特征提取

在雷达波束的照射下目标所表现出来的回波特性是雷达进行目标探测与识别的根本特征信息。常用的雷达目标特征信息包括目标的雷达散射截面(RCS)、一维距离像、二维ISAR像，以及角闪烁和多普勒信息等[23]。

对目标进行一维和多维成像时，需要计算一定带宽或角度范围内各个采样点处目标的单站散射场信息。以二维ISAR成像为例，假定要求的成像口径范围为，两个维度的分辨率分别为和，则对雷达信号的带宽和姿态角变化范围有如下要求[24]：

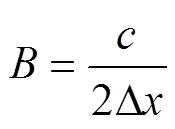
(37)

同时，频域采样间隔和角度采样间隔需满足：

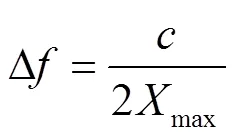
(39)

5.2 应用案例

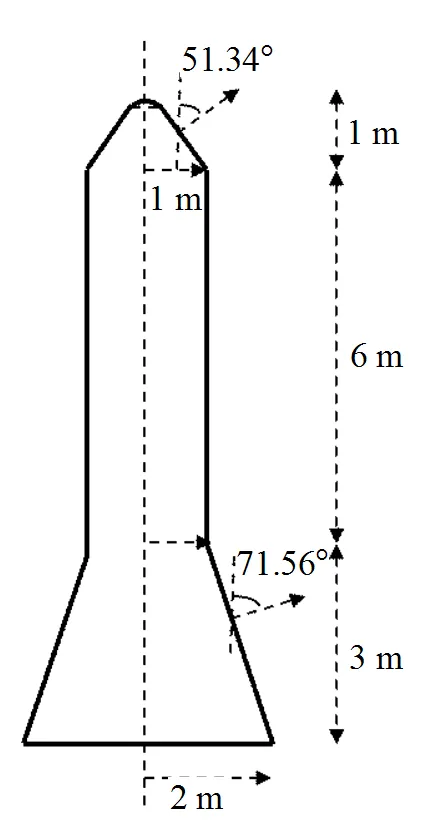
图7 导弹模型示意图

以某型导弹为例，如图7所示，将该导弹分解为钝头锥、圆柱和圆台3个基本电磁散射计算单元。其中，钝头锥高1.1 m，底面半径为1 m，由一个圆台(1=1 m,2=0.2 m,1=9 m,2=10 m)和椭球冠(1=0.2 m,2=2 m,1=10 m,2=10.1 m)相切组合而成；圆柱半径为1 m，高6 m；圆台上下底面半径分别为1 m和2 m，高3 m。利用参数化组合建模及计算方法对其RCS、一维距离像和二维ISAR图像进行快速仿真计算。

RCS仿真频率=1 GHz，雷达入射波的方位角为0o，俯仰角从0o开始以0.5o为步进增加至180o，通过本文方法快速计算得到的单站RCS与多层快速多极子(MLFMA)精确数值仿真方法[25]的计算结果对比如图8所示。由图可见，两种计算方法得到的目标随入射角(俯仰角)变化所表现出的散射特性的趋势是一致的。该算例中，即使基于24个核心的高性能工作站进行计算，MLFMA算法耗时2.6 h才能得到图中所示的一条单站RCS曲线，占用计算机内存33.5 GB。而本文开发的组合参数建模方法在普通的笔记本电脑上单核运算仅耗时2 s，占用内存250 MB，可满足实时计算的应用需求。

采用相对均方根误差对两种计算结果的差异进行衡量。对于该导弹模型，参数化组合(本文方法)计算结果与MLFMA结果的相对均方根误差仅为0.5%。可见对于导弹目标，参数化组合建模计算得到的RCS具有非常高的精度：

RCS曲线随俯仰角变化在51.5o、71.5o和90o共3个角度出现峰值，这和导弹模型的钝头圆锥侧面法线、截头圆锥侧面法线，以及圆柱体法线方向保持一致，在这些角度刚好有较强的镜面反射。在0o和180o出现的峰值刚好和导弹顶部和底部的镜面反射保持一致。

为了得到导弹的一维距离像信息，设置轴向观测范围为15 m，距离分辨率为0.25 m，雷达波中心频率为1 GHz，根据式(36)和式(38)计算得到观测频率范围为GHz，频率采样间隔MHz，共需61个采样频点。图9给出了分别采用本文方法和MLFMA算法计算得到的导弹模型在轴线上()的一维距离像对比。

雷达回波信号峰值主要由不连续结构处的感应电流引起。因此雷达回波信号标识的距离像信息与导弹物理尺寸能够非常准确地对应。由图可见，虽然各个散射峰的幅度略有差异，但两种分析方法都能准确地标识导弹模型的距离像信息。同时观测到在MLFMA的距离像中多了一个与爬行波对应的散射峰。这是因为MLFMA通过数值方法精确求解麦克斯韦方程，可模拟物体各部件间的电磁耦合和精确描述物体表面的感应电流分布；而本文方法的算法基础是物理光学近似，无法模拟爬行波的贡献。

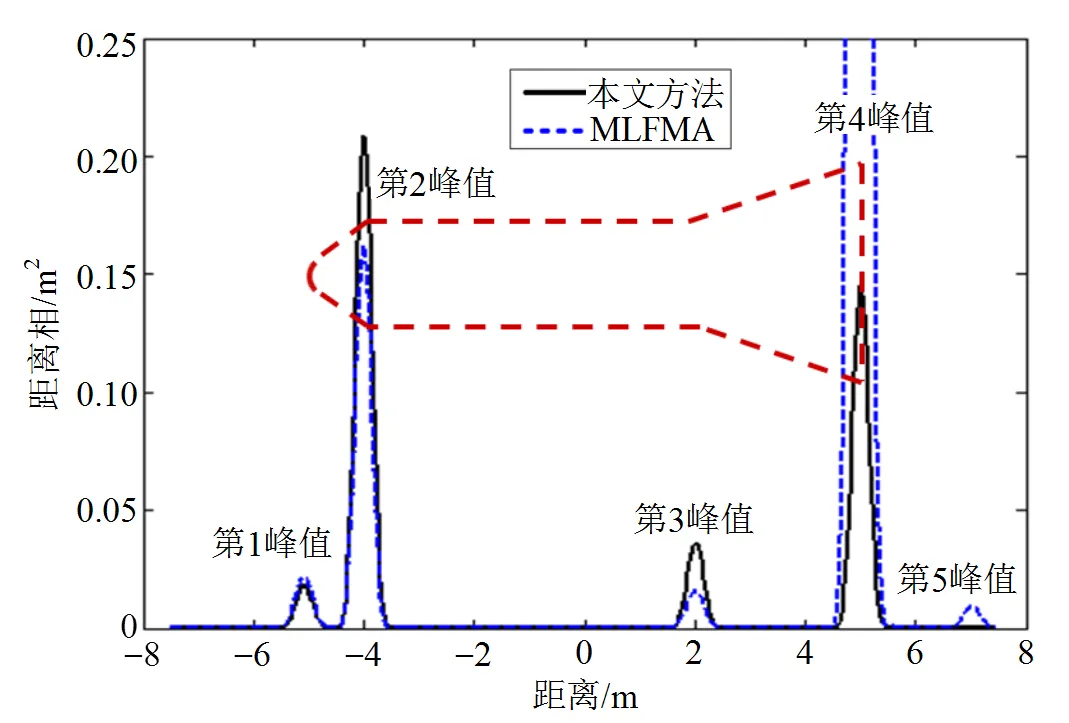
图9 导弹模型一维距离像对比

进一步对导弹模型进行二维ISAR像分析。设置径向(距离维)观测范围为15 m，距离分辨率为0.25 m，横向(方位维)观测范围为10 m，空间分辨率为0.2 m，雷达信号中心频率为1 GHz，中心观测角度为。由式(36)～式(39)计算得到频率范围为GHz，频率采样间隔MHz，角度范围为，角度采样间隔，对应61个频率采样点和51个角度采样点，需3 111次单站散射计算。若基于MLFMA精确数值算法，在24个核心的高性能工作站上计算需要耗时约30 h，才能完成该ISAR图像提取。而基于本文提出的参数化组合建模和快速数值仿真方法，在普通的PC机上运行时间不到30 s就可完成仿真分析。由图10可见，ISAR图像中的散射热点分布与导弹的物理结构几乎完全一致。

通过以上的应用案例分析不难看出，参数化组合建模及计算方法基本能够实现导弹目标电磁散射特性的实时计算，仿真精度满足工程应用需求。这为总体方案设计时，对调整外形参数后目标散射特性快速估算提供了有效的实现途径，并为试验方案验证提供了高效的解决手段。

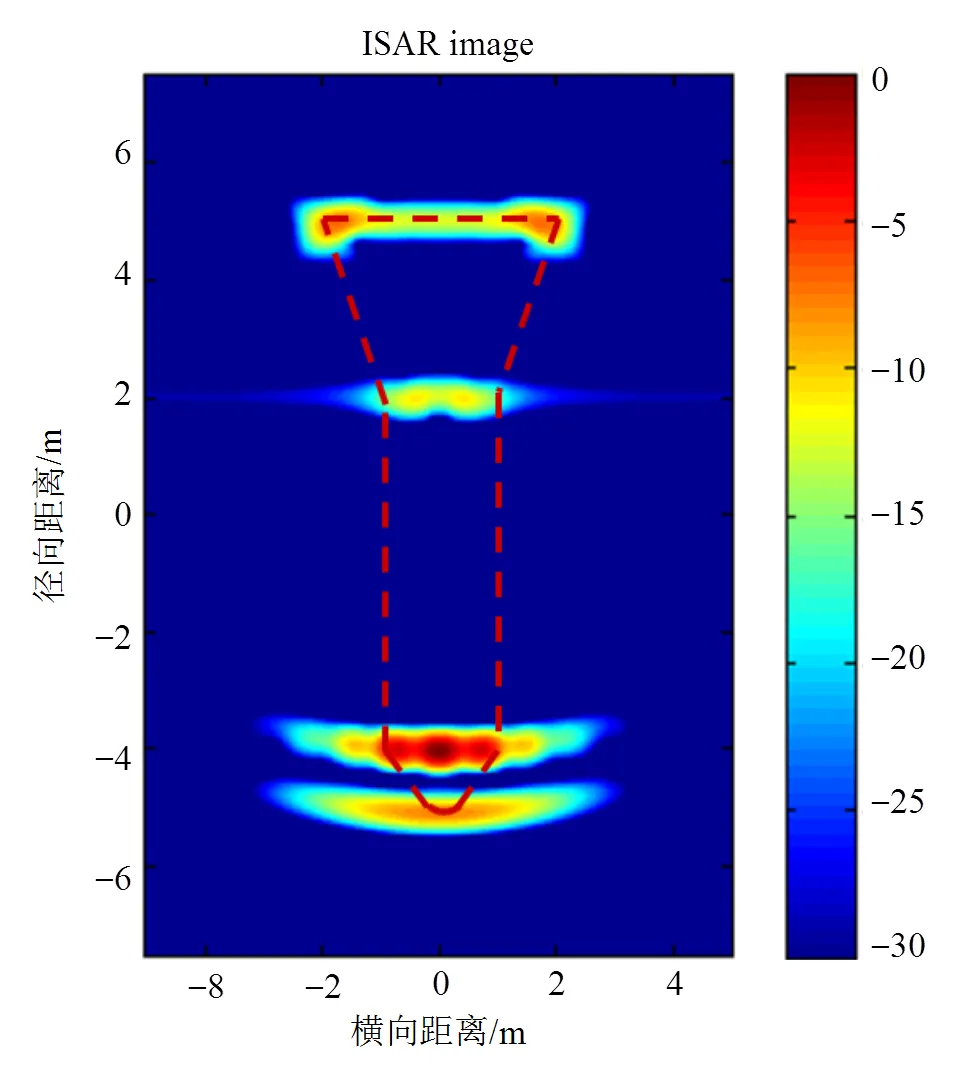
图10 导弹模型二维ISAR像

6 结束语

本文以靶场飞行试验方案设计需求为牵引，基于平板、圆柱、圆台和球冠等基本几何体单元对导弹目标进行参数化组合建模。基于高频近似，采用物理光学方法和边缘绕射理论对各基本单元的电磁散射特性进行解析计算。通过参数化组合建模、散射场解析计算和矢量场叠加的方法，快速仿真得到导弹目标的电磁散射数据。结果表明，该方法基本能实现导弹目标RCS的实时高精度计算，开发的仿真软件为基于方案验证需求的导弹目标RCS快速计算与评估提供了有力支持。

此外，软件还具有一维距离像、二维ISAR像的仿真计算能力，为目标电磁散射特征提取提供了有力支撑。

[1] 聂在平. 目标与环境电磁散射特性建模—理论、方法与实现[M]. 北京: 国防工业出版社, 2009.

NIE Zai-ping. Modeling of electromagnetic scattering characteristics of target and environments-theory, method and realization[M]. Beijing: National Defense Industry Press, 2009.

[2] 庄钊文, 袁乃昌, 莫锦军, 等. 军用目标雷达散射截面预估与测量[M]. 北京: 科学出版社, 2007.

ZHUANG Zhao-wen, YUAN Nai-chang, MO Jin-jun, et al. Prediction and measurement of radar cross section for military targets[M]. Beijing: Science Press, 2007.

[3] 傅君眉, 冯恩信. 高等电磁场理论[M]. 西安: 西安交通大学出版社, 2000.

FU Jun-mei, FENG En-xin. The advanced electromagnetic field theory[M]. Xi'an: Xi'an Jiaotong University Press, 2000.

[4] 方宙奇, 孟敏. 电磁场数值方法[M]. 成都: 电子科技大学出版社, 2012.

FANG Zhou-qi, MENG Min. Numerical methods for electromagnetic fields[M]. Chengdu: University of Electronic Science and Technology of China Press, 2012.

[5] 盛新庆. 计算电磁学要论[M]. 北京: 中国科学技术大学出版社, 2008.

SHENG Xin-qing. Computational electromagnetics[M]. Beijing: University of Science and Technology of China Press, 2008.

[6] 张京国, 梁晓庚. 基于物理光学法和面元法的目标近场RCS计算[J]. 探测与控制学报, 2008, 30(6): 42-45.

ZHANG Jing-guo, LIANG Xiao-geng. Calculating near-field RCS of targets based on physical-optics method and panel method[J]. Journal of Detection & Control, 2008, 30(6): 42-45.

[7] 严俊. 参数曲面上的高频渐进方法研究与应用[D]. 成都: 电子科技大学, 2015.

YAN Jun. Research and application of parametric surface based high frequency asymptotic methods[D]. Chengdu: University of Electronic Science and Technology of China, 2015.

[8] KNOTT E F. A progressing of high-frequency RCS prediction techniques[J]. Proc IEEE, 1985, 73(2): 252-264.

[9] MICHAELI A. Equivalent edge currents for arbitrary aspects of observation[J]. IEEE Transactions on Antennas and Propagation, 1984, 32(3): 252-258.

[10] STRATTON J A. Electromagnetic theory[M]. New York: McGraw-Hill, 1941.

[11] KNOTT E F. Radar cross section measurements[M]. New York: Springer Science & Business Media, 2012.

[12] 马振华. 现代应用数学手册[M]. 北京: 清华大学出版社, 2005.

MA Zhen-hua. Handbook of applied mathematics applied mathematics handbook[M]. Beijing: Tsinghua University Press, 2005.

[13] CHEW W C. 非均匀介质中的场与波[M]. 聂在平, 柳清伙, 译. 北京: 电子工业出版社, 1992.

CHEW W C. Waves and fields in inhomogeneous media[M]. Translated by NIE Zai-ping, LIU Qing-huo. Beijing: Publishing House of Electronics Industry, 1992.

[14] 《数学手册》编写组. 数学手册[M]. 北京: 高等教育出版社, 1979.

"Mathematics Handbook" Compilation Group. Mathematics handbook[M]. Beijing: Higher Education Press, 1979.

[15] 徐宏枢. 三轴椭球面的面积计算[J]. 渝州大学学报, 1998, 15(1): 57-60.

XU Hong-shu. The calculation of the area of the 3-axes ellipsoid[J]. Journal of Yuzhou University.1998, 15(1): 57-60.

[16] CONDE O M, PEREZ J, CATEDRA M F. Stationary phase method application for the analysis of radiation of complex 3-D conducting structures[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(5): 724-731.

[17] KELLER J. Geometrical-theory of diffraction[M]. New York: McGraw-Hill, 1958.

[18] KOUYOUMJIAN R G, PATHAK P H. A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface[J]. Proceedings of the IEEE, 1974, 62(11): 1448-1461.

[19] SHORE R A, YAGHJIAN A D. Application of incremental length diffraction coefficients to calculate the pattern effects of the rim and surface cracks of a reflector antenna[J]. IEEE Transactions on Antennas & Propagation, 1993, 41(1): 1-11.

[20] UFIMTSEV P Y. Method of edge waves in the physical theory of diffraction[M]. Moscow: Soviet Radio, 1962.

[21] 崔索民, 吴振森. PTD和PTDEEC算式的奇异点处理[J]. 电波科学学报, 1997, 4(12): 369-374.

CUI Suo-min, WU Zhen-sen. Treatment of singularities in PTD and PTDEEC[J]. Chinese Journal of Radio Science, 1997, 4(12): 369-374.

[22] Mathworks. 面向科学计算的MATLAB和Simulink [EB/OL]. [2016-09-10]. http://cn.mathworks.com.

Mathworks. Model-Based Design with MATLABand Simulink[EB/OL]. [2016-09-10]. http://cn.mathworks.com.

[23] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005.

HUANG Pei-kang, YIN Hong-cheng, XU Xiao-jian. Characteristics of radar targets[M]. Beijing: Publishing House of Electronics Industry, 2005.

[24] OZDEMIR C. Inverse synthetic aperture radar imaging with MATLAB algorithms[M]. Manhattan, America: John Wiley & Sons,Inc, 2012.

[25] 胡俊. 复杂目标矢量电磁散射的高效方法－快速多极子方法及其应用[D]. 成都: 电子科技大学, 2000.

HU Jun. The efficient method for vector electromagnetic scattering from complex object-fast multipole method and its application[D]. Chengdu: University of Electronic Science and Technology of China, 2000.

编 辑 税 红

Compositional Modeling and Electromagnetic Scattering Characteristics Extracting for Missile Targets

HE Shi-quan1, WANG Tong1, WANG Xu1, and DANG Hong-jie2

(1. School of Electronic Engineering, University of Electronic Science and Technology of China Chengdu 610054; 2.Key Laboratory of Space Object Measurement Haidian Beijing 100089)

In this paper, conventional missile targets are divided into basic scattering cells, such as disks, cylinders, cones and ellipsoids. By carrying on the parameterized compositional modeling, analytical calculation of integrals, and superposition the field contribution of each unit, we can obtain the scattering fields of missile-like objects in time. Consequently, the electromagnetic scattering characteristics such as RCS, the range profile and ISAR images are available. The numerical results demonstrate the proposed method can meet the real-time requirement as well as the high precision. Numerical software is developed and it gives a best support to the RCS calculation and design evaluation of missile targets in engineering application.

diffraction of edges; ISAR image; parameterized compositional modeling; physical optics method; rangel profile; RCS

TN951

A

10.3969/j.issn.1001-0548.2017.02.001

2016-09-18；

2016-12-06

国家自然科学基金(61301057, 61231001)

何十全(1984-)，男，博士，副教授，主要从事计算电磁学、电磁兼容及电波传播方面的研究.