环形单级倒立摆系统的改进PSO-PID控制研究
赵文才,金朝永
(广东工业大学 应用数学学院,广州 510520)
环形单级倒立摆系统的改进PSO-PID控制研究
赵文才,金朝永
(广东工业大学 应用数学学院,广州 510520)
为实现环形单级倒立摆的稳定性控制,设计了一种改进的基于粒子群算法的积分分离PID控制算法.首先通过拉格朗日方程推导出环形单级倒立摆系统的数学模型,然后用matlab计算发现系统不稳定,因此需要设计外部控制器加以调节.本文提出了改进粒子群算法(PSO)来整定PID控制器参数,在此基础上设计了一种改进的积分分离的PID控制器,在比例和积分项前加入连续变化的函数作为系数以防止积分饱和.最后在matlab中分别用基PSO-PID控制和基于改进积分分离的PSO-PID控制对环形单级倒立摆进行仿真.仿真结果表明,在改进积分分离的PSO-PID控制下,系统中连杆和摆杆的超调量均下降至0,调节时间分别缩短至0.8s和0.9s.这说明本文设计的控制方法能有效使环形单级倒立摆在较短的时间内达到稳定.
拉格朗日方程; 环形倒立摆; 粒子群算法; 积分分离; 积分饱和
Abstract: In order to realize the stability control of the single-stage inverted pendulum,an improved integral separation PID control algorithm based on particle swarm optimization is designed.First,the mathematical model of the single-stage inverted pendulum system is deduced by the Lagrangian equation,and then the system is unstable by matlab,so it is necessary to design the external controller to adjust it.Then,an improved particle swarm optimization algorithm (PSO)is proposed to set the parameters of the PID controller.On this basis,an improved integral-separated PID controller is designed to add the continuously changing function as a coefficient before the ratio and integral to prevent integral saturation.Finally,in the matlab,the PSO-PID control and the PSO-PID control based on the improved integral separation are used to simulate the single-stage inverted pendulum.Under the control of PSO-PID with improved integral separation,the overshoot of connecting rod and pendulum in the system decreased to 0,and the adjustment time is shortened to 0.8s and 0.9s respectively.The control method designed in this paper could effectively stabilize the single-stage inverted pendulum in a short time.
Key words: Lagrangian equation,rotary inverted pendulum,particle swarm algorithm,integral separation,integral saturation
0 引言
环形倒立摆系统是一个多变量、非线性、强耦合的绝对不稳定的单输入多输出的系统.倒立摆的稳定性控制是控制理论的典型应用[1].以前人们主要研究的是直线轨道型的小车倒立摆系统的控制问题,而环形倒立摆系统是一个典型的非线性系统,相比于直线型的倒立摆系统,它具有多个自由度,克服了行程限制,是校验各种控制理论的更为简单的试验设备[2].目前,环形倒立摆系统的稳定控制研究有PID控制、LQR控制、滑模控制、模糊控制等.对上述控制方法进行的优化算法有遗传(GA)算法、粒子群算法(PSO),人工蜂群算法等.本文利用粒子群算法(PSO)全局能力强、需要调整的参数不多、具有更快的收敛速度等特点来整定PID控制器参数.普通PID容易出现积分饱和的现象,对此进行的改进方法有积分分离、抗饱和积分、带死区的积分、微分先行等.而积分分离又有分段式积分分离和连续型积分分离.为保证引入积分后,系统的稳定性不变,本文用连续型积分分离方法,对比例项做出了改进,即在积分发生作用后,使比例系数相应地减少.
1 环形一级倒立摆系统的数学模型
1.1 模型建立
在忽略各种阻力和摩擦的条件下,环形一级倒立摆系统可以简化为一个连杆、一个质量块和一个摆杆.其坐标系如图1所示,各物理量的参数值见表1.其中连杆的长度为l1; 摆杆长度为l2; 连杆相对于y轴的转角为θ1; 摆杆与垂直向上方向的夹角为θ2(逆时针方向为正).这是一个二自由度系统,连杆在水平面内做圆周运动,通过耦合作用带动摆杆运动,以使摆杆进入工作状态.所谓工作状态,就是摆杆相对于不稳定平衡点为θ2=0,摆杆的θ2角保持在一定范围内.
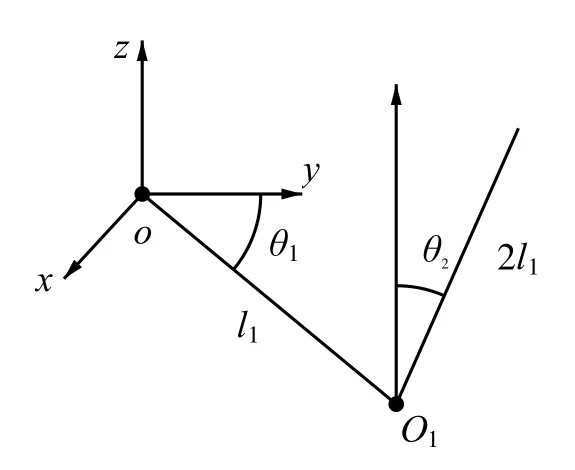
图1 环形一级倒立摆的坐标系

表1 环形一级倒立摆各物理量的参数值
在离摆杆转动轴O1距离为l处取一小段dl,这一小段的坐标为
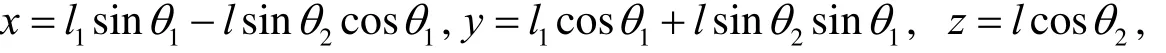
则得到该小段的动能
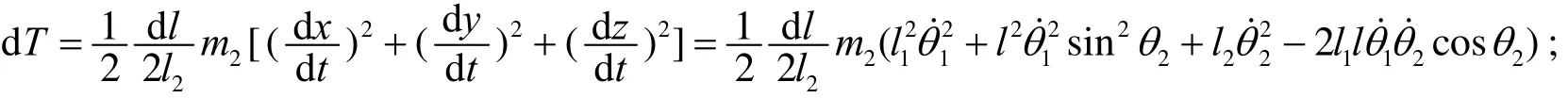
连杆的动能
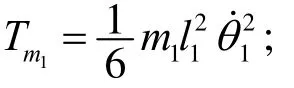
摆杆的动能

质量块的动能

从而系统的总动能为
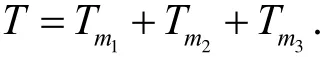
以连杆水平位置为零势能面,则水平连杆的势能

摆杆的势能
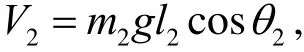
质量块的势能

从而系统的总势能为
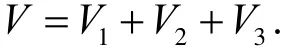
设系统的广义坐标为q={q1,q2},构建拉格朗日算子

根据拉格朗日方程

其中Qi(i=1,2)为广义外力.又在广义坐标θ2上无外力,于是系统的运动方程为

经整理得
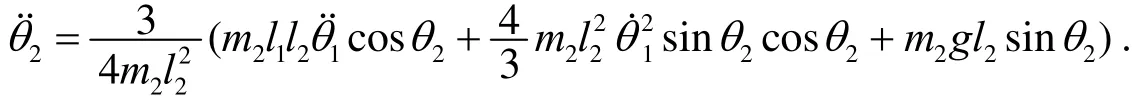
将上式写成函数的形式:

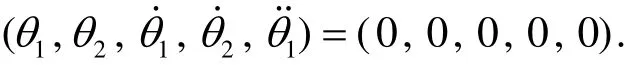
将(*)式在平衡位置进行泰勒级数[3]展开,并线性化,即

经过拉普拉斯变换可得到传递函数为
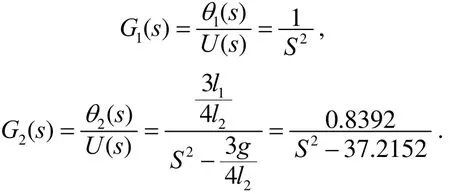
以水平连杆所受外力Q1作为输入,则有μ=Q1,输出变量为y=(θ1,θ2)T,设系统的态变量为
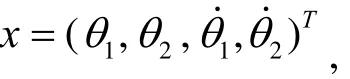
则可以将运动微分方程转化为状态空间形式:
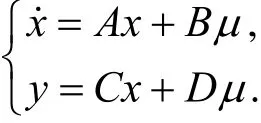
其中

1.2 系统的稳定性、能控性和能观性分析
利用matlab函数eig(A)计算得到特征根为[0,0,6.1004,−6.1004],特征值有正实部,可见系统有右半平面的极点,因此该系统是不稳定的,需要施加外部控制器.经计算
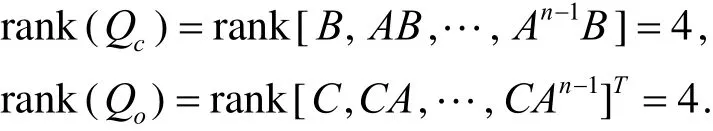
因此,本文所研究的环形单级倒立摆系统是不稳定、能控、能观测的.
2 基于粒子群算法的PID控制器设计
2.1 PID 控制原理
PID 控制分为模拟式PID控制和数字式PID控制.模拟式PID控制以模拟的连续控制系统为基础,它由模拟PID控制器和被控对象等组成.给定值r(t)与实际输出值y(t)存在控制偏差为

PID 控制器将偏差e(t)的比例(P)、积分(I)和微分(D)通过线性组合构成控制量,对被控对象进行控制.
PID 的控制规律为
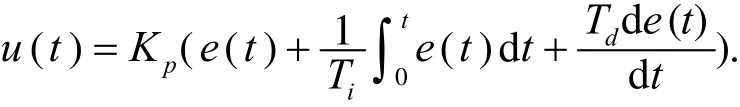
或写成传递函数的形式:
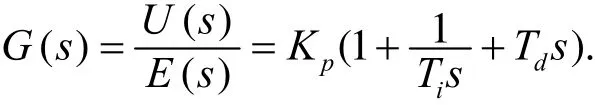
其中Kp为比例系数;Ti为积分时间常数;Td为微分时间常数.

2.2 基于粒子群(PSO)[4]的PID控制器参数整定
利用粒子群算法来优化PID参数,其本质是基于一定目标函数的参数寻有问题,即在Kp,Ki,Kd三个变量的参数空间中寻找最优值使系统的控制性能达到最优,其控制方框图如图2所示.
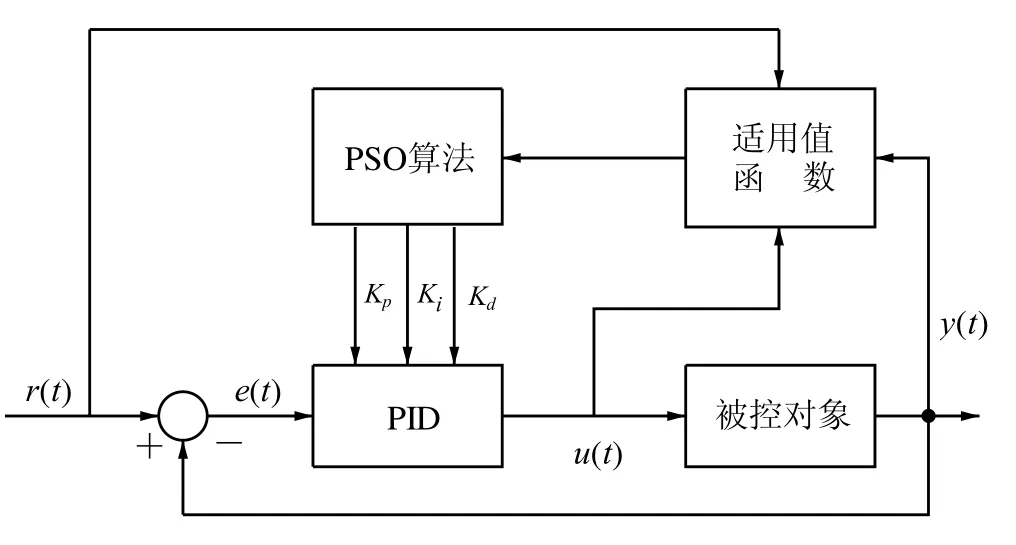
图2 粒子群优化算法PID参数整定方框图
利用粒子群算法优化 PID 参数的步骤如下:
(1)初始化与算法参数设置
(2)计算每个微粒的适应值
为防止控制能量过大并保证系统响应的快速性,适应值函数[5]如下:
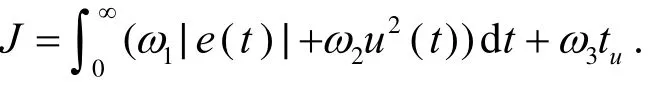
其中ω1,ω2,ω3为权重,tu为连杆达到平衡状态的时间,u(t)为PID控制器输出.
在适应值函数中引入惩罚功能以防止产生超调,即一旦产生超调,便将超调量作为适应值函数中的最主要的一个项目,此时的适应值函数变为
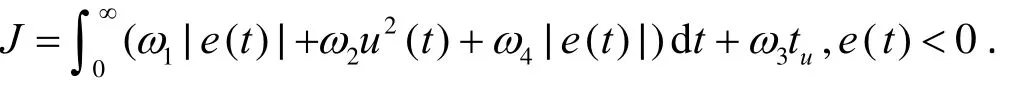
这里ω4>>ω1.
(3)选出个体最优值和全局最优值
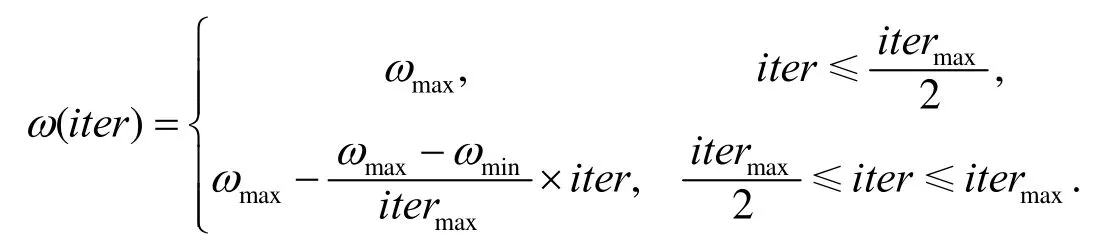
其中itermax为最大迭代次数,iter为当前迭代次数.
(ⅱ)异步学习因子[7]
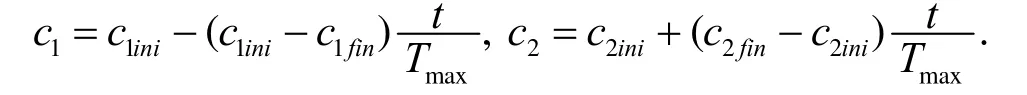
其中c1ini,c2ini表示学习因子c1,c2的初始值;c1fin,c2fin表示学习因子c1,c2的迭代终值;t,Tmax分别表示迭代次数和最大迭代次数.
(5)对微粒的速度和位置进行更新
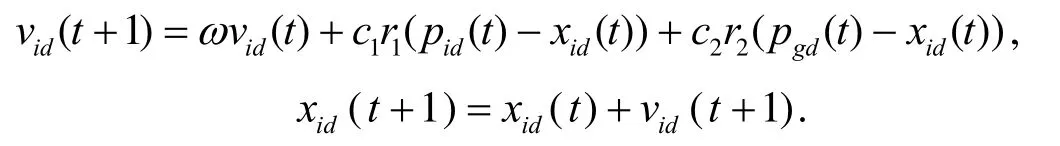
(6)计算优化性能指标
若性能指标达到算法终止条件,循环结束,否则返回步骤(2),继续下一个循环.
本文选取微粒数为40个,微粒维数为 3维,进化代数为40,r1,r2是在(0,1)之间产生的随机数,粒子位置和速度的区间范围为[0,5]和[−2.5,2.5].学习因子中的参数c1ini=2.5,c1fin=0.5,c2ini=2.5,c2fin=0.5,权重系数参数ω1,ω2,ω3,ω4的取值分别为0.999,0.001,100.000,2.000.
将上文给出的环形一级倒立摆系统连杆和摆杆的传递函数运用到PSO优化算法中对PID参数进行整定.先画出普通PID的输出曲线,然后画出整定后的曲线,结果如图3所示.
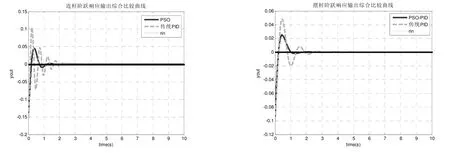
图3 PSO和传统PID的输出综合比较曲线
控制器参数见表2.
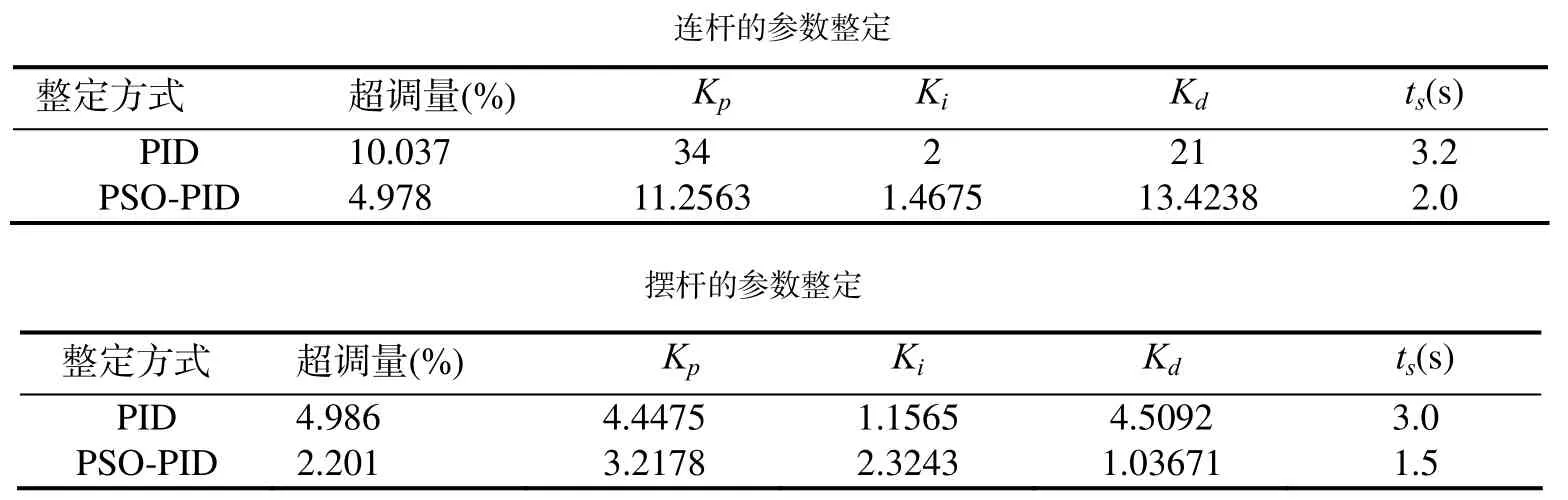
表2 PSO整定PID控制器参数表
可以很明显的看出: 基于 PSO算法的控制器对系统的调节时间更短,连杆和摆杆的角度的超调量更小,系统取得了很好的控制效果.
3 PID控制器设计
3.1 改进积分分离的PID控制
本文采用增量式PID的控制算法,其控制算法可以描述为
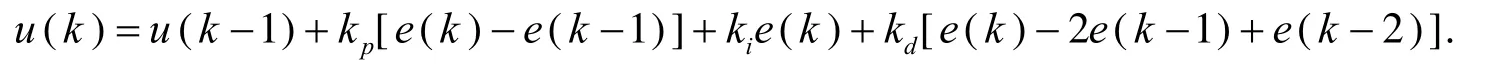
在此基础上,为防止积分饱和,需要对PID控制器进行改进,而积分分离法可以有效抑制饱和.积分分离可以在积分项加入系数,这个系数可以是分段函数[8]也可以是连续函数[9].但分段时的次数和每一段的偏差值范围不好把握,实际情况较为复杂,且分段会使积分的利用效率降低.因此本文选择下列连续函数作为积分项的系数:

其中a为常数,为给定的误差最小阈值.
为保证积分作用引入后系统的稳定性不变,需要将kp的值相应变小[10].于是将控制算法作如下改变:
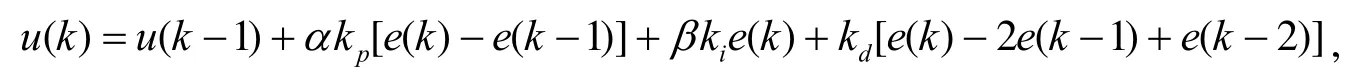
其中α=e-|e(k)|.
这时比例项和积分项同时进行了调节.
3.2 仿真实验
试验对象为环形倒立摆系统,输入试验参数,a=0.08,误差最小阈值1e-6.下面将改进的积分分离PID控制方法运用于环形倒立摆系统的稳定性控制中,并与基于改进粒子群算法的PID控制进行比较,结果如图4所示.

图4
由图4可知,积分分离后,连杆和摆杆的输出曲线有明显的超调量下降,用粒子群(PSO)整定后,连杆的超调量为4.978%,摆杆的超调量为2.201%,改进积分分离后,连杆的超调量为0%,摆杆的超调量为0%.此外,连杆和摆杆达到稳定的时间也有较明显的减少,PSO算法整定后,连杆和摆杆分别在2.0s和1.5s达到稳定状态,改进积分分离后,连杆和摆杆分别在0.8s和0.9s后达到稳定状态.因此,本文方法对PID控制器的改进是有效的.
4 结论
本文首先利用拉格朗日原理建立了环形一级倒立摆的数学模型,然后用改进的粒子群算法对倒立摆系统进行了整定.通过连杆和摆杆的输出曲线可以看出,改进的粒子群算法对PID控制器参数能够有效整定.连杆和摆杆的输出曲线表明,本文提出的改进型积分分离PID控制算法可以弥补超调和波动的缺陷,具有更快的响应速度,调整时间明显缩短,使环形倒立摆系统的连杆和摆杆在较短时间内具有良好的稳定性品质.
[1]PARKM,KIMYJ,LEEJJ.Swing-up Control for an Inverted Pendulum with Restricted Cart rail Length[J].International Journal of Control,Automation and System,2009,7(4): 674
[2]王东亮,刘 斌,张曾科.环形一级倒立摆摆起及稳定控制研究[J].微计算机信息,2007,(04): 1~2,14
[3]胡小兵,刘成忠,赵晓军.环形一级倒立摆系统单神经元PID控制仿真[J].甘肃农业大学学报,2016,(05): 132~136
[4]胡 伟,徐福缘.基于改进粒子群算法的PID控制器参数自整定[J].计算机应用研究,2012,(05): 1791~1794
[5]王东云,徐艳平,瞿博阳,等.基于动态多组群PSO的倒立摆最优控制器设计[J].自动化应用,2016,(10): 31~34,95
[6]于 洋,王子帅,杨 青.改进PSO-PID算法在温度控制中的快速性研究[J].工业仪表与自动化装置,2013,(01): 9~11
[7]赵志刚,黄树运,王伟倩.基于随机惯性权重的简化粒子群优化算法[J].计算机应用研究,2014,(02): 361~363,391
[8]张亚飞,陈红波,冯小华,等.PID控制算法及其积分项的改进[J].科技创新与应用,2013,(24): 66~67
[9]蔡逢煌,杨富文,林 鸿.改进型积分分离PID控制的设计[J].福建电脑,2003,(09): 41~42
[10]孟祥萍,寇 磊,苑全德,等.基于改进型积分分离式PID的机器人运动控制[J].东北电力大学学报,2016,(05): 86~91
Improved PSO - PID Control of Single Rotary Inverted Pendulum System
ZHAO Wencai,JIN Chaoyong
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)
O231; TP13
A
1672-5298(2017)03-0006-07
2017-06-18
赵文才(1991− ),女,湖南娄底人,广东工业大学应用数学学院硕士研究生.主要研究方向: 系统与控制

