DES算法解析

◆艾奇昆



DES算法解析

◆艾奇昆

（辽宁省信息中心 辽宁 110002）

从技术层面上说，密码学始终是信息安全的一个核心技术，而对称密码体制中的DES算法一直以来都作为数据加密的标准，本文主要介绍DES算法流程的基本原理及加密过程，旨在用最通俗易懂的方式对该算法进行阐述，使广大爱好者对DES算法能有更深入的了解。

DES；密钥；异或

0 引言

DES（Data Encryption Standard）算法是世界上最常用的加密算法。在很长时间内，许多人心目中“密码生成”与DES一直是个同义词。目前网络上有许多介绍DES算法的文章，也有许多博客则直接给出晦涩难懂的源码，缺乏解读，让人误解；事实上，DES算法并不复杂，只是流程繁多而已。本文旨在用最通俗易懂的方式对该算法进行阐述，使广大密码学爱好者对DES算法流程能有更深入的了解。

1 DES历史

DES全称为Data Encryption Standard，即数据加密标准，是一种使用密钥加密的算法，1973年5月，美国国家标准局下发了红头文件，征求加密算法来保护传输过程中的数据。国家标准局等了很久一直没有人投标，一直到1974年8月6日，IBM才拿出了自己开发的一套代号LUCIFER的标准。美国安全局评估后，在1977年7月15日采用了LUCIFER的一个变种作为数据加密标准DES。

DES很快被非数字媒体采用，比如电话线中的信号加密。在那些年里，国际香料组织IFF曾用DES来加密那些用电话线传输的秘密配方。同时，作为政府之后第二大急需加密的银行业也将DES作为广泛应用的标准。

2 DES算法工作原理

DES是一个基于组块的加密算法，这意味着无论输入还是输出都是64位长度的。也就是说DES产生了一种最多264种的变换方法。每个64位的区块被分为2个32位的部分，左半部分L和右半部分R（这种分割只在特定的操作中进行）。虽然DES算法输入是64位长度，但是它的密钥长度却是56位。比如，取明文M = 0123456789ABCDEF这里的M是16进制的，将M写成二进制（4位二进制数对应1位十六进制数），我们得到一个64位的区块：

M = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

L = 0000 0001 0010 0011 0100 0101 0110 0111

R = 1000 1001 1010 1011 1100 1101 1110 1111

DES使用56位的密钥操作这个64位的区块。密钥实际上也是储存为64位的，但每间隔的第8位都没有被用上（也就是第8，16，24，32，40，48，56，和64位都没有被用上）。但是，我们仍然在接下来的运算中将密钥标记为从1到64位的64个比特。不过，你也许会看到，刚刚提到的这8个在创建子密钥的时候会被忽略掉。

举个例子，取十六进制密钥K为：K = 133457799BBCDFF1

我们可以得到它的二进制形式（1为0001，3为0011.依次类推，并且将每八位写成一组）：

2.1 创建48位子密钥

这个64位的密钥首先根据如下规定的PC-1表格（位数排列表）进行变换：

PC-1表

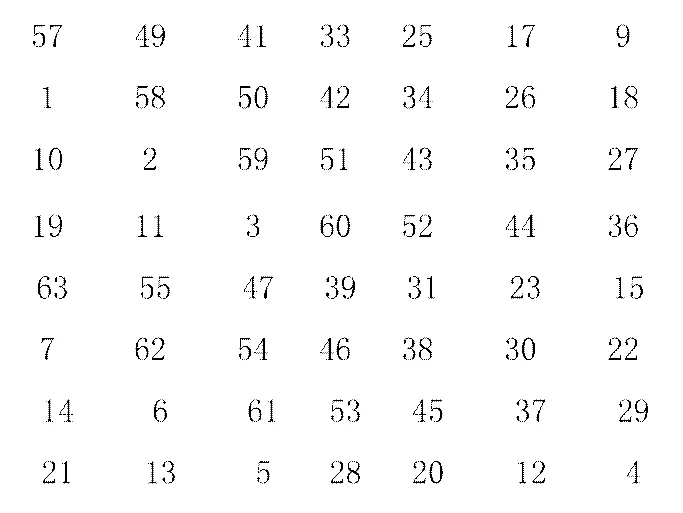
具体的变换规则为：将密钥K转换成的二进制数，按照位数对应的PC-1表格顺序重新排列，既第一个元素为57，那么原密钥的第57位变换为新密钥K+的第1位。同理，原密钥的第49位变换为新密钥的第2位……原密钥的第4位变换为新密钥的最后一位。注意原密钥中只有56位会进入新密钥，上表也只有56个元素。具体变换过程如下：

这样就得到了56位的新密钥，然后，将这个密钥拆分为左右两部分，C0和 D0，每半边都有28位。如下所示：

C0= 1111000 0110011 0010101 0101111

D0= 0101010 1011001 1001111 0001111

对相同定义的C0和D0，我们现在创建16个块Cn和 Dn，1<=n<=16。每一对Cn和Dn都是由前一对Cn-1和 Dn-1移位而来。具体说来，对于n = 1，2，…，16，在前一轮移位的结果上，使用如下表格进行二进制数的左移操作。左移操作的具体过程是指将除第一位外的所有位往左移一位，并将第一位移动至最后一位。

例如：对于CandD是CandD移位而来的，具体来说，通过2次左移位；CandD则是由CandD通过1次左移得到的。通过以上操作，我们就可以得到如下的CandD排列表：

C= 1111000011001100101010101111

D= 0101010101100110011110001111

C= 1110000110011001010101011111

D= 1010101011001100111100011110

C= 1100001100110010101010111111

D= 0101010110011001111000111101

C= 0000110011001010101011111111

D= 0101011001100111100011110101

C= 0011001100101010101111111100

D= 0101100110011110001111010101

C= 1100110010101010111111110000

D= 0110011001111000111101010101

C= 0011001010101011111111000011

D= 1001100111100011110101010101

C= 1100101010101111111100001100

D= 0110011110001111010101010110

C= 0010101010111111110000110011

D= 1001111000111101010101011001

C= 0101010101111111100001100110

D= 0011110001111010101010110011

C= 0101010111111110000110011001

D= 1111000111101010101011001100

C= 0101011111111000011001100101

D= 1100011110101010101100110011

C= 0101111111100001100110010101

D= 0001111010101010110011001111

C= 0111111110000110011001010101

D= 0111101010101011001100111100

C= 1111111000011001100101010101

D= 1110101010101100110011110001

C= 1111100001100110010101010111

D= 1010101010110011001111000111

C= 1111000011001100101010101111

D= 0101010101100110011110001111

接下来，我们还需要按照表PC-2将变换得到Cn和 Dn转变成新密钥Kn（1<=<=16）：

PC-2表

原来每对子密钥有56位，但按照PC-2表变成仅仅使用其中的48位。于是，第n轮的新密钥Kn 的第1位来自组合子密钥CnDn的第14位，第2位来自第17位，依次类推，知道新密钥的第48位来自组合密钥的第32位，比如，对于第1轮的组合密钥C1D1= 1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110通过PC-2表变换后：

得到：

K1=000110 110000 001011 101111 111111 000111 000001 110010，按照以上的组合规律，依次组合得到：

K2= 011110 011010 111011 011001 110110 111100 100111 100101

K3= 010101 011111 110010 001010 010000 101100 111110 011001

K4= 011100 101010 110111 010110 110110 110011 010100 011101

K5= 011111 001110 110000 000111 111010 110101 001110 101000

K6= 011000 111010 010100 111110 010100 000111 101100 101111

K7= 111011 001000 010010 110111 111101 100001 100010 111100

K8= 111101 111000 101000 111010 110000 010011 101111 111011

K9= 111000 001101 101111 101011 111011 011110 011110 000001

K10= 101100 011111 001101 000111 101110 100100 011001 001111

K11= 001000 010101 111111 010011 110111 101101 001110 000110

K12= 011101 010111 000111 110101 100101 000110 011111 101001

K13= 100101 111100 010111 010001 111110 101011 101001 000001

K14= 010111 110100 001110 110111 111100 101110 011100 111010

K15= 101111 111001 000110 001101 001111 010011 111100 001010

K16= 110010 110011 110110 001011 000011 100001 011111 110101

2.2 加密每个数据的64位区块

对于明文数据M，我们还要计算一个初始变换IP（）。IP是重新变换数据M的每一位产生的。产生过程由以下IP表决定：

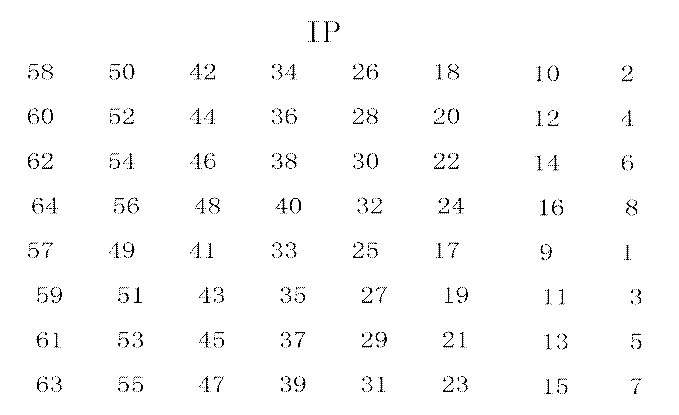
这里M的第58位是1，变成了IP的第1位。M的第50位是1，变成了IP的第2位。M的第7位是0，变成了IP的最后一位。例如对于明文M=0123456789ABCDEF，经过如下变换后结果IP为：

IP = 1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010，接着将变换得到的IP分为32位的左半边L0和32位的右半边R0，对于上例，我们得到：

IP = 1100 1100 0000 0000 1100 1100 1111 11111111 0000 1010 1010 1111 0000 1010 1010

L0= 1100 1100 0000 0000 1100 1100 1111 1111

R0= 1111 0000 1010 1010 1111 0000 1010 1010

接着我们还需执行16轮迭代，对1<=<=16，使用一个函数f。函数f输入两个区块：一个32位的数据区块和一个48位的密钥区块K，输出一个32位的区块。定义+表示异或（XOR）。那么让n从1循环到16，我们计算：

LR

RLRK

这样我们就得到最终区块，也就是n=16的L16R16。具体说这个过程就是，我们拿前一个迭代的结果的右边32位作为当前迭代的左边32位。对于当前迭代的右边32位，将它和上一个迭代的f函数的输出执行异或（XOR）运算。剩下的就是f函数是如何工作的了。为了计算f，我们首先拓展每个Rn-1，将其从32位拓展到48位。这是通过使用一张表来重复Rn-1中的一些位来实现的。我们称这个过程为函数E。也就是说函数E（Rn-1）输入32位输出48位。

定义E为函数E的输出，将其写成8组，每组6位。这些比特是通过选择输入的某些位来产生的，具体选择顺序按下表实现：

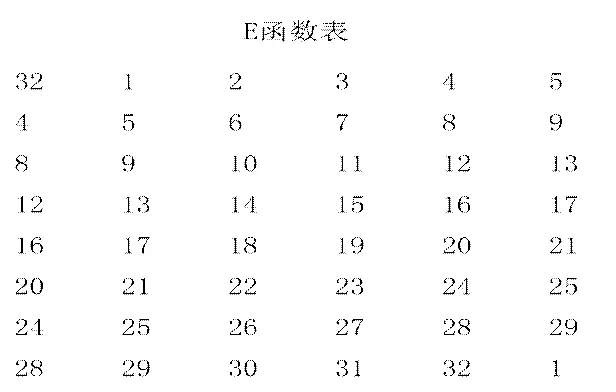
也就是说E（Rn-1）开头的三个比特分别来自Rn-1的第32、1和2位。E（Rn-1）末尾的2个比特分别来自Rn-1的第32位和第1位。比如，给定R0，我们可以计算出E（R0），具体过程如下：

接着在f函数中，我们对输出E（Rn-1）和密钥执行XOR运算：Kn+E（Rn-1），二进制数的XOR（⊕）运算规则为：两个二进制数进行异或运算，相同的则为0，不同的则为1，比如，对K1，E（R0），我们有：

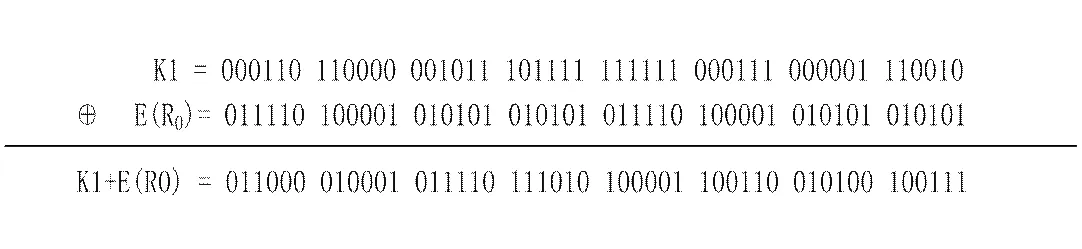
到这里我们还没有完成f函数的运算，我们仅仅使用一张表将Rn-1从32位拓展为48位，并且对这个结果和密钥Kn执行了异或运算。我们现在有了48位的结果，或者说8组6比特数据。我们现在还要对每组的6比特执行一些特殊的操作：我们将它作为一张被称为“S盒”的表格的地址。每组6比特都将给我们一个位于不同S盒中的地址。在那个地址里存放着一个4比特的数字。这个4比特的数字将会替换掉原来的6个比特。最终结果就是，8组6比特的数据被转换为8组4比特（一共32位）的数据。将上一步的48位的结果写成如下形式：Kn+E（Rn-1）B1B2B3B4B5B6B7B8每个B都是一个6比特的分组，我们现在计算S1（B1）S2（B2）S3（B3）S4（B4）S5（B5）S6（B6）S7（B7）S8（B8），其中，SB指的是第i个S盒的输出。为了计算每个函数SSS，取一个6位的区块作为输入，输出一个4位的区块。例如决定S的表格如下：

如果S是定义在这张表上的函数，B是一个6位的块，那么计算S的方法是：B的第一位和最后一位组合起来的二进制数决定一个介于0和3之间的十进制数（或者二进制00到11之间）。设这个数为i。B的中间4位二进制数代表一个介于0到15之间的十进制数（二进制0000到1111）。设这个数为j。查表找到第i行第j列的那个数，这是一个介于0和15之间的数，并且它是能由一个唯一的4位区块表示的。这个区块就是函数S输入得到的输出S。比如，对输入第一位是0，最后一位是1，决定了行号是01，也就是十进制的1 。中间4位是1101，也就是十进制的13，所以列号是13。查表第1行第13列我们得到数字5。这决定了输出；5是二进制0101，所以输出就是0101。也即S（011011）= 0101，同理，定义其余函数SS的表格如下所示：

S2

15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10

3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5

0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15

13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9

S3

10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8

13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1

13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7

1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12

S4

7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15

13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9

10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4

3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14

S5

2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9

14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6

4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14

11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3

S6

12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11

10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8

9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6

4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13

S7

4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1

13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6

1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2

6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12

S8

13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7

1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2

7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8

2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11

例如：对于第一轮，我们得到这8个S盒的输出：

K+（R）= 011000 010001 011110 111010 100001 100110 010100 100111

SBSBSBSBSBSBSBSB= 0101 1100 1000 0010 1011 0101 1001 0111

函数f的最后一步就是对S盒的输出进行一个变换来产生最终值：=（SBSB…SB）。

变换P由如下表格定义：

P输入32位数据，通过变换产生32位输出，比如，对于8个S盒的输出：

SBSBSBSBSBSBSBSB= 0101 1100 1000 0010 1011 0101 1001 0111具体变换过程如下：

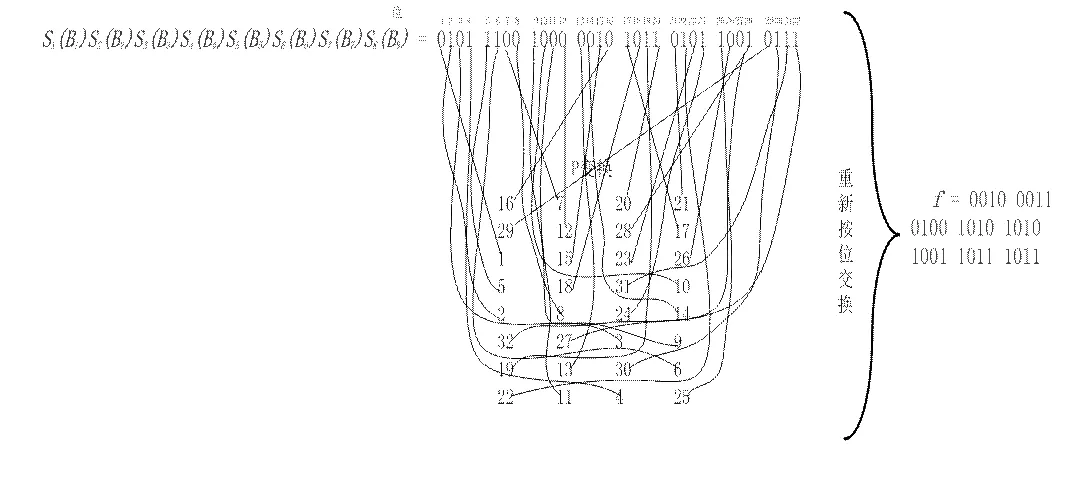
图5 变换过程图

最终，我们得到= 0010 0011 0100 1010 1010 1001 1011 1011，那么，R=L+RK，即再执行异或+（XOR）操作：

1100 1100 0000 0000 1100 1100 1111 1111 + 0010 0011 0100 1010 1010 1001 1011 1011 = 1110 1111 0100 1010 0110 0101 0100 0100

在下一轮迭代中，我们的L=R，这就是我们刚刚计算的结果。之后我们必须计算R=L RK，一直完成16个迭代。在第16个迭代之后，我们有了区块LandR。接着我们逆转两个区块的顺序得到一个64位的区块：RL然后对其执行一个最终的变换IP，其定义如下表所示：

也就是说，该变换的输出的第1位是输入的第40位，第2位是输入的第8位，一直到将输入的第25位作为输出的最后一位，比如，如果我们使用了上述方法得到了第16轮的左右两个区块：

L16= 0100 0011 0100 0010 0011 0010 0011 0100

R16= 0000 1010 0100 1100 1101 1001 1001 0101

我们将这两个区块调换位置，然后执行最终变换：R16L16= 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100，再按照IP-1执行最终的变换，具体变换过程如下：

写成16进制得到：85E813540F0AB405，这就是明文M = 0123456789ABCDEF的加密密文C = 85E813540F0AB405，至此整个DES加密过程结束。

3 结束语

最后再补充3DES加密算法的相关知识，它是DES加密算法的一种模式，它使用3条64位的密钥对数据进行三次加密。3DES是DES的一个更安全的变形。它是以DES为基本模块，通过组合分组方法设计出的更为安全的分组加密算法。

目前，在中国尤其是金卡工程的全面启动，DES算法在POS、ATM、磁卡及智能卡（IC卡）、加油站、高速公路收费站等领域被广泛应用，以此来实现关键数据的保密。信用卡持卡人的PIN的加密传输，IC卡与POS间的双向认证、金融交易数据包的MAC校验等，均用到DES算法。

[1]（美）帕尔，（美）佩尔茨尔著，马小婷译.深入浅出密码学—常用加密技术原理与应用[M].北京：清华大学出版社，2012.

[2]罗守山等编著.密码学与信息安全技术[M].北京：北京邮电大学出版社，2009.

[3]张文政，陈克非，赵伟.密码学的基本理论与技术[M].北京：国防工业出版社，2015.