一种基于指纹特征比特串和级联编码的生物加密方案

◆陈卓洋 方勇 谢承洋



一种基于指纹特征比特串和级联编码的生物加密方案

◆陈卓洋 方勇 谢承洋

（四川大学电子信息学院 四川 610064）

本文主要研究以指纹为对象的生物特征加密技术。生物特征加密技术是生物识别技术与密码学的有机结合。由生物特征生成的密钥既可以对数据直接进行加密也可以对密钥进行加密保护，并且具有不易被盗、被遗忘，不易破解等优点。本文提出了一种基于指纹特征比特串的加密方案，首先将指纹信息转换为比特串，再运用两级串行级联的纠错编码，保护密钥或者秘密信息。实验结果表明，该方案安全性较高，系统开销较小，并且能够保护用户指纹特征信息，具有一定的实际应用价值。

生物加密；模板保护；纠错编码；级联编码

0 引言

传统的口令或密码已难以保障信息系统的安全，而基于生物特征的身份认证技术，已广泛地应用于金融、国防、电子商务等领域。然而，随着人们对生物特征识别技术的深入研究，逐渐发现生物特征识别技术存在一些固有的安全隐患和缺陷：由于生物特征的唯一性，一旦丢失则是永久性的丢失。这使得生物特征隐私保护成为一个重要的安全问题。

生物特征加密技术是生物特征识别技术与传统密码学技术的有机融合，该技术将生物特征与密码技术用某种方式相结合，为密钥和生物特征模板提供一种全新的安全保护措施，可有效解决上述安全问题。

1 相关研究

目前，国内外有大量的专家和机构对生物特征模板保护技术展开了研究，并在指纹、掌纹、视网膜、虹膜、静脉、脸型、等生物特征方面取得了一定的成果。本文主要针对个人指纹特征进行研究。1994年A.Bodo首先提出将密钥和生物特征相结合，使用生物特征保护密钥[1]。1999年等人提出了模糊金库（）方案[2]，其核心思想是将生物特征信息隐藏于大量的干扰信息之中，只有合法用户才能过滤除干扰信息继而获得密钥的使用权。等人在2010年提出了一种基于指纹细节点比特串的模板保护方案[3]。其基本思想是将指纹信息进行安全域转换，提取指纹特征比特串，然后通过计算注册模板和活体模板对应的比特串的相似度来判断指纹是否同源。2015年茹宇[4]对的方案进行了改进，引入混沌序列，生成可撤销模板，提高了抗交叉模板攻击性能。唐宇[5]在的基础上，对比特串的生成技术进行了改进，将三维投影降到二维投影，减短了二进制位数，提高了系统效率。但是此方案必须存储原始注册指纹二进制串信息，一旦攻击者获得指纹模板读取顺序，那么就可以从特征比特串恢复出原始指纹信息，从而导致用户隐私信息泄露。之后，[6]等人在的基础上将比特串和BCH编码结合，提出了一种基于模糊承诺的加密方案，降低了误识率和拒识率，同时没有直接存储指纹特征比特串，进一步保护了指纹模板安全。但是其方案的耗时较大，系统效率较低。针对方案存在的问题，本文提出一种改进的加密方案，运用两级级联的纠错编码方案，增加信息冗余，降低匹配用时，提高系统性能。

2 基于指纹特征比特串和级联纠错编码的生物加密方案

2.1 指纹信息安全域转换

指纹信息在实际中信息量是无限大的，而且直接储存指纹图像信息极易造成丢失风险。因此，对于指纹信息首先通过不可逆变换，要将其转换到安全域进行处理。本文运用唐宇[5]提出的改进的指纹比特串生成方案，将生成的特征向量投影到二维矩阵空间，量化读取矩阵空间数值，生成比特串，组成比特串矩阵，实现指纹信息的安全域转换。实现方案如下：首先利用模式识别已有图像技术进行预处理[7]，提取指纹原始细节点，计算每两点之间的相对特征向量，用以表示其在指纹图像中的相对位置，然后建立二维空间矩阵，将其投影到矩阵中，并量化标记此矩阵，之后以可变的顺序遍历它，生成一个细节点对应的特征比特串，最后将每个细节点的特征比特串组合在一起组成指纹特征比特串矩阵。

2.2 模糊承诺思想

生物特征具有模糊性，也可以看作具有噪声的随机信号，即使是同一个生物特征再次提取时，最多能获得与注册生物模板时比较接近但不完全相同的特征信息，但是对于传统密码技术而言，用作加解密的密钥数据必须是完全一致的。为了解决这个难题，[8]等人将纠错编码技术和传统加密技术想结合提出了模糊承诺算法，其基本思想是：用散列函数隐藏原始码字，但是公开偏差，用来向证据提供具有弹性的辅助信息以便能够解开承诺。模糊承诺算法包括承诺与解承诺两个阶段。在承诺阶段用证据来承诺码字，其中和的长度均为，证据可以用和偏差来唯一表示，承诺包含{，}，其中为承诺码字的散列函数值。在解承诺阶段，用户输入证据，然后计算，如果与足够相似，进一步可以通过计算与的散列函数值是否相等来验证解承诺是否成功。算法示意框图如图1所示。

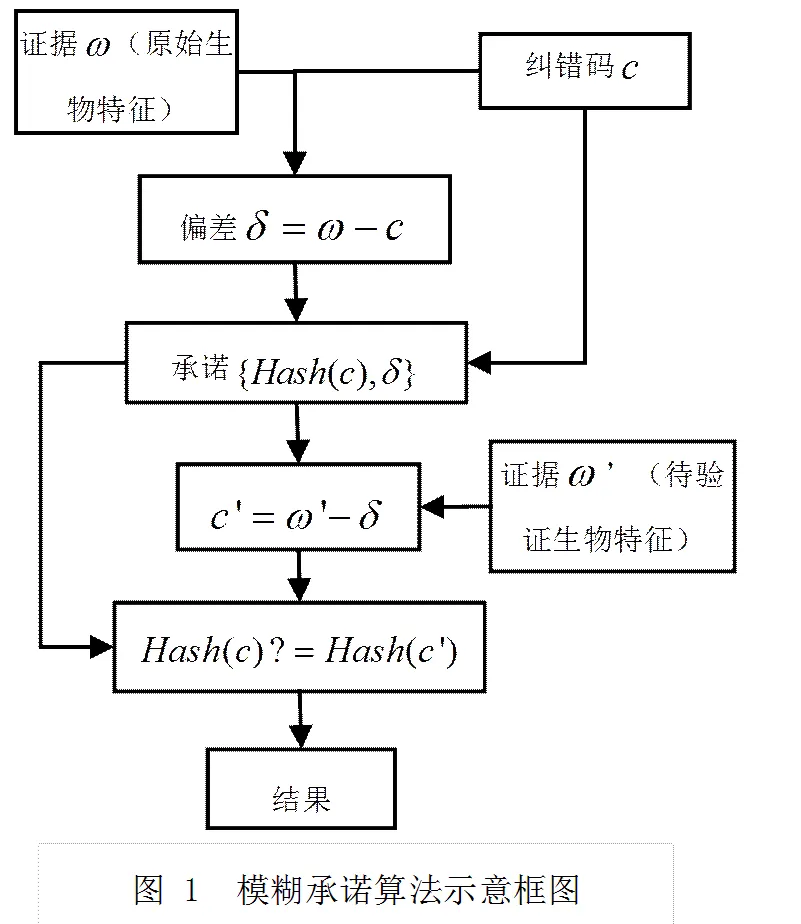
在模糊承诺方案中纠错编码技术起着至关重要的作用，正是因为纠错编码的使用才能克服生物加密系统中生物特征具有的模糊性和随机性。在的方案中，采用了编码技术。本方案对其进行改进，采用码和卷积码两级级联的方案。这样的优势在于：一是因为两级译码处理较之同等长度的单级译码而言，复杂度要小得多[12]。二是两级级联方案能产生较大信息冗余，从而提高信息的安全性。三是码适合纠随机错误，而采用级联方案，可以选取不同纠错编码来实现既能纠随机错误，也能纠突发错误。

码是一种特殊的非二进制码，它定义在伽罗华域2上，其中每个符号由位比特组成。由于码是以符号为单位实现对差错的控制的，因此特别适合于纠正突发错误。记码为nk，其中k表示编码前的符号数，n表示编码后的符号数，表示该码可以纠正的错误个数，各参数满足如下约束关系：n-k=2。

卷积码是一种非分组码，其主要特点是编码器是有记忆的，因此适合纠正随机错误。记卷积码为nk，其中k表示编码前的比特数，n表示编码后的比特数，表示存储器的个数。编码器在任意时刻的n个输出不仅与该时刻的k个输入有关，还与该时刻个存储器中的状态（即前个时刻的输入）有关。

2.3 方案实现

方案的基本思路是，首先从原始指纹图像中提取出固定的长度为的特征比特串，然后采用模糊承诺算法思想，首先随机产生一个，经过纠错编码后产生一个长度为的密钥，并与长度同样为的指纹特征比特串进行异或操作，所得的结果存储为生物特征模板，并抛弃原始的。在解密时如果用于比对的指纹和原始指纹来自同一个人，那么解密成功，恢复出。方案总体流程如图2所示。

加密阶段，将一个随机生成的二进制密钥编码为与指纹特征比特串长度相同的二进制序列，之后将此编码后的二进制随机序列与特征比特串矩阵相异或，生成生物密钥K。此过程具有单向性，即由生物密钥K无法导出随机密钥或原始指纹信息。

解密阶段，则首先从用户的指纹中提取指纹细节点特征比特串矩阵H′，再用此特征比特串矩阵和存储的K异或，异或的结果再解编码，若解码成功且通过哈希值验证后恢复得到密钥′。

下文将详细说明具体细节。

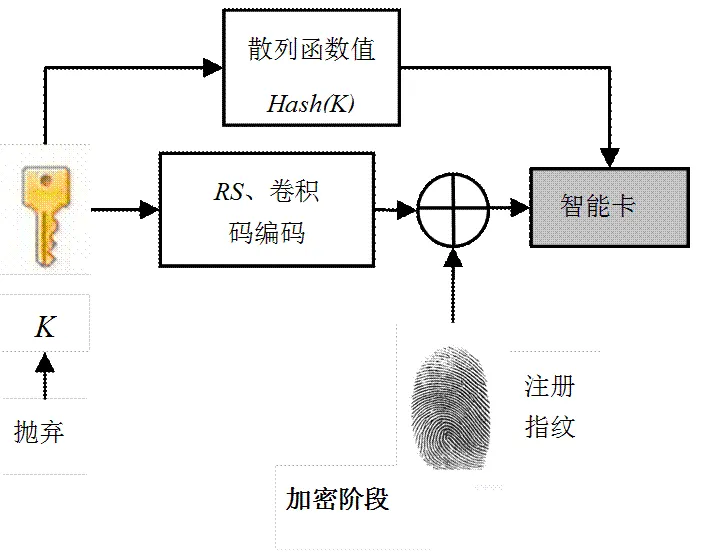
2.3.1 加密阶段

（1）从用户注册指纹中提取指纹特征比特串，长度为。系统随机生成二进制密钥，之后采用编码算法，将进行一次编码，然后用卷积码进行二次编码，编为长度同样为的二进制序列K。计算密钥的散列函数值（），并将抛弃。

（2）将编码后的二进制序列K与指纹特征比特串矩阵H中的每一个特征比特串β相异或，得到得到个二进制序列并组成加锁矩阵K，并将其存储在智能卡中。

2.3.2 解密阶段

（1）从系统数据库中提取矩阵K。采集待验指纹，提取指纹特征比特串，得到由个特征比特串b组成的特征比特串矩阵H′。

（2）依次从特征比特串矩阵中取出第个比特串，并与系统数据库中的K进行异或。得到个二进制序列K。

（3）用卷积码和RS码解码算法对个二进制序列K进行纠错解码，若解码成功则恢复出密钥，否则，回到（2）继续从b中取出下一个比特串，直到遍历完所有的b，若仍无法成功，则密钥生成失败并结束。

（4）计算密钥的散列函数值（），判断（）是否等于（），若相等则说明=并输出密钥作为最终密钥。否则，密钥生成失败并结束。

3 实验测试与性能分析

本文采用2012编程环境，采用公开指纹库。同时，由于公开库质量较差，我们实际采集了80个指纹，作为实际采集指纹库进行对比。

3.1 实验参数选取

本文采用的纠错编码算法中，需要确定两级纠错编码，即nk和nk的参数。卷积码的编码参数，我们根据文献给出的最优卷积码，即（4，1，6）卷积码。码采用定义在（2）上的编码，即=1。由此可得，随机密钥的长度由公式（1）确定。

k=k×m-v （1）

由编码特性，k=n/m-2t，得出随机密钥和编码后的长度，码的容错位数之间的关系如公式（2）。

2）

由此可知，需要确定三个参数。只需确定其中两个参数，就可确定第三个参数。

3.1.1 参数n的选取

编码后码元的长度等于特征比特串的长度而特征比特串长度取决于二维空间矩阵的长宽和矩阵单元的长宽。参数的数值选取应尽量使同源指纹对应比特串之间的相似度较高，而不同源的指纹特征比特串较低。特征比特串的相似度可以由公式（3）计算。

实验中，分别采用公开指纹库和实际采集指纹库中的80幅指纹图像进行测试，这80幅指纹图像采集于8个不同的手指，每个手指采集10次。将每个指纹图像进行特征比特串提取操作，然后计算同源指纹（即真匹配）和不同源指纹（即假匹配）特征比特串的平均相似度。表1列举了指纹库的和实际采集指纹测试结果。

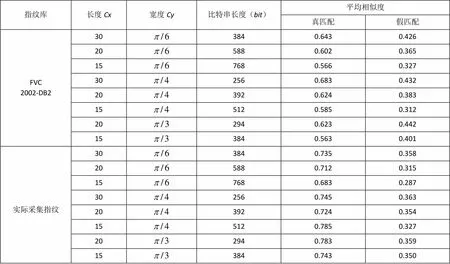
表1 不同配置参数下的真假匹配情况

综合真假匹配平均相似度以及比特串长度，对于指纹库和实际采集指纹库都选取特征比特串长度=512作为最优参数，即编码长度==512。

3.1.2 参数t的选取

参数的选择应使合法用户提供的特征比特串通过纠错后能够与模板比特串一致，而非法用户提供的特征比特串在容错能力下无法完成纠错，进而无法恢复出正确密钥。

实验采用从指纹库中的80幅指纹图像对生成的特征比特串进行实验分析，分别计算同源指纹对应比特串、同源非对应比特串及非同源指纹比特串的错误位数，并分别记录其中2000次的比对结果。如图3所示。从实验结果发现同源指纹的对应比特串的错误位数与非同源指纹比特串及同源非对应比特串错误位数之间的具有明显的区分度，可以选取一个恰当的阈值作为容错位数t的取值范围。

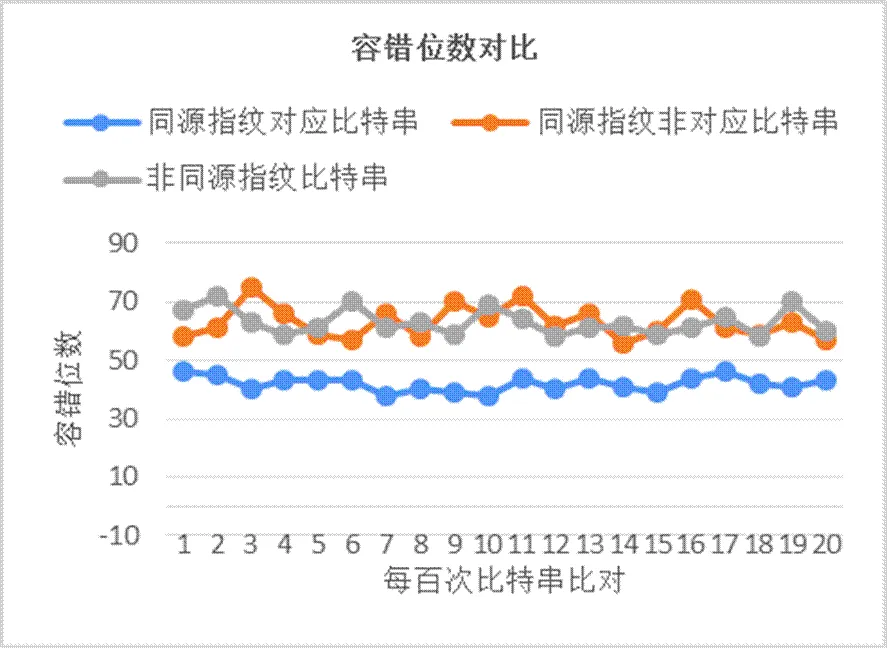
图 3 指纹特征比特串容错位数对比示意图

经过实验得出同源指纹对应比特串之间的平均错误位数为约为42位，而非同源指纹比特串的平均容错位数为62位，阈值可以设置在42位到62位之间，即42<4<62。此外，从理论上讲，的取值会对拒识率（）和误识率（）造成影响。在一定范围内，若的取值越大拒识率会降低，误识率会增大，相反，若的取值越小拒识率会增大，误识率会降低。在实际使用中，可以根据需求和测试需要以此值为基准，上下浮动选取的取值。

3.2 实验结果分析

实验分别选取指纹库中的80幅指纹图像和实际采集的80幅指纹图像进行实验测试。其中有560次为真匹配，其余为假匹配。计算在不同级联方案下的拒识率（）和误识率（），结果如表2所示。方案的曲线如图4所示。

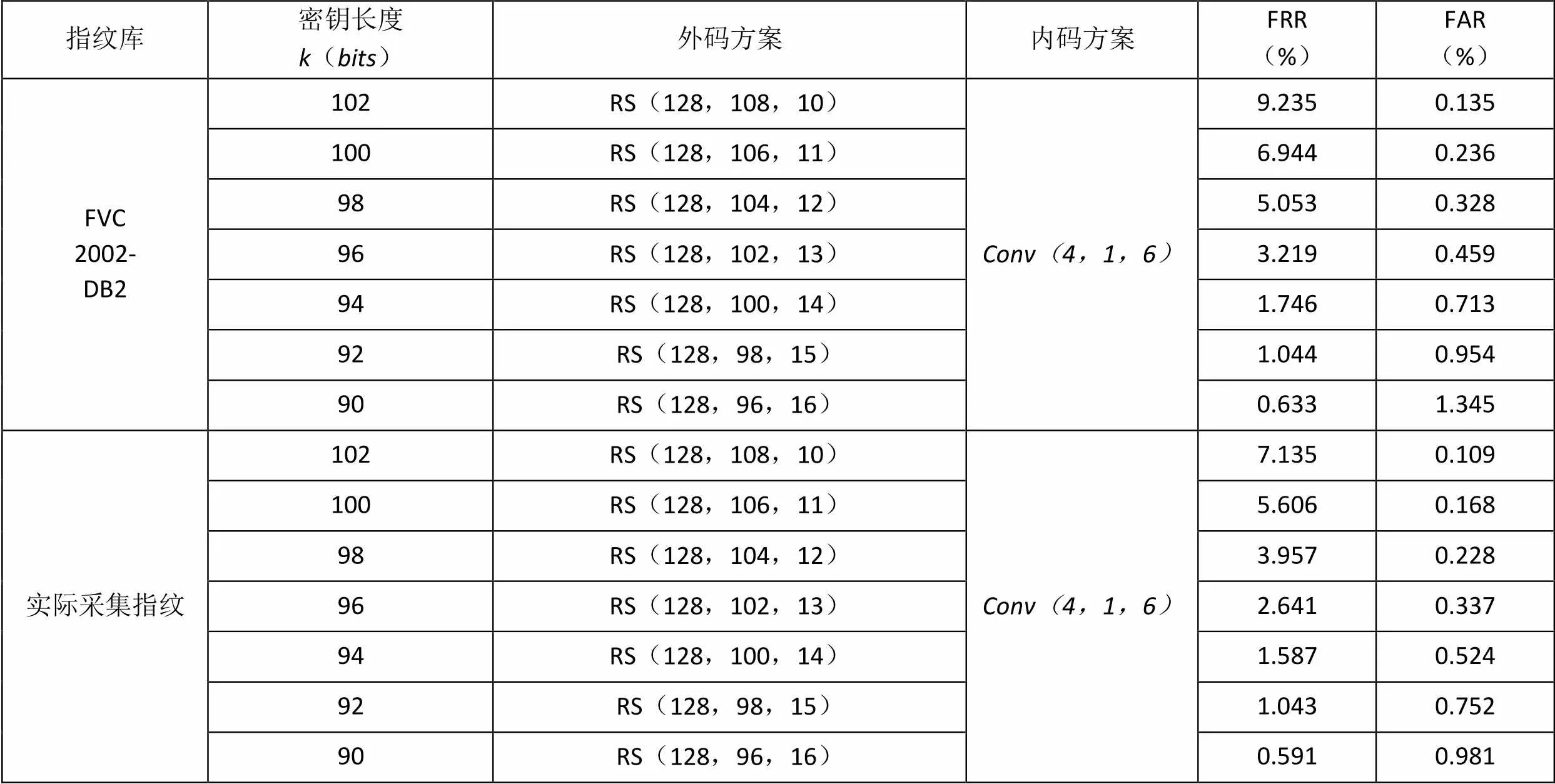
表2 不同级联方案下的拒识率和误识率

从表2显示的实验结果可以看出，该方案的拒识率（）和误识率（）可以获得比较理想的测试结果。同时随着容错位数的增大，拒识率（）会降低，但误识率（）会升高。而且由于实际采集指纹质量较好，测试结果也优于。在实际运用中，可以参考图4所示的曲线，根据不同的应用需求与场合来选择不同的参数，以更好的满足主要应用目的。

本文提出方案与方案相比，鉴别性能稍有提高，但是由于级联方案在编码效率上比单级编码高，译码耗时少[12]，时间开销比XIE的方案降低至少20%。同时，信息冗余度方面，的方案为0.872，本方案为0.199，增加了大量冗余，安全性更高。

3.3 安全性分析

3.3.1 抗暴力破解攻击

（1）针对指纹模板的暴力攻击方面，本方案的整个过程中均不需要存储原始指纹信息，而只需要存储辅助信息，即经过与编码后的随机密钥进行异或后的指纹特征比特串，而辅助信息的生成是一个不可逆的过程，无法从辅助信息获得指纹特征信息，因此暴力破解在计算上是不可行的。而针对密钥的暴力攻击，本文采用（128，102，13）和（4，1，6）级联方案，若攻击者想直接生成编码后的二进制序列BCH，那么他必须生成512位二进制序列，其中52位允许容错，那么他成功的概率为2-460。

（2）若攻击者想直接生成密钥，那么正确的概率为2-96。

（3）若攻击想生成用散列函数加密之后的密钥，则安全性取决于散列函数的安全性，散列函数加密后的密钥长度通常为128或256位，则成功的概率为2-128或2-256。

3.3.2 抗多模板交叉匹配攻击

在指纹特征模板安全域转换过程中，提取到的指纹比特串由单元矩阵的取值和访问量化标记后的二维矩阵的顺序这两个参数决定，而这两个参数决定了提取的比特串的长度，这样一来采用长度为的比特串提取方案，就有！个顺序可供选择。因此，在实际系统中，只要通过设置不同的参数，即可以使从同源指纹中提取的两个比特串完全不同，无法进行匹配，从而可以抵抗同源指纹的多模板交叉匹配攻击。

4 结束语

本文研究了指纹信息的安全域转换，然后对基于纠错编码的加密方案提出了改进方案，采用级联编码代替单级编码，在提高安全性的同时降低了系统开销，具有一定的实际应用价值。指纹信息和密码学的有机结合，必将为指纹识别技术带来更加广阔的应用前景。

[1]A.Bodo.；Method for Producing a Digital Signature with AidofaBiometricFeature [P]. GermanPatent：DE42-43-908-A1，1994.

[2]Juels A.，Sudan M.；A Fuzzy Vault scheme[C]. Proc of International Symposium on Information Theory [S.l.]：IEEE Press，2002.

[3]Chulhan Lee，Jaihie Kim，Cancelable fingerprint templates using minutiae-based bit-strings [J].Journal of Network and Computer Applications，2010.

[4]茹宇.基于混沌序列的指纹特征模板保护技术研究[D].成都：四川大学，2015.

[5]唐宇.基于指纹比特串的生物特征加密技术研究与应用[D].成都：四川大学，2015.

[6]Cheng-Yang XIE，Jia-Yong LIU，Xu YAO，Dian-Hua TANGA. Research of Biometric Key Generation Based on Fingerprint Bit-strings.Journal of Fiber Bioengineering and Informatics，2015.

[7]李昊，傅曦.Visual C++指纹模式识别系统算法与实现[M].人民邮电出版社，2008.

[8]Juel A，and Wattenberg M. A fuzzy commitment scheme[C]. Proc. Of the 6th ACM Conf. Computer and Comm. Security（CCCS），1999.

[9]Andre Neubauer，Jurgen Freudenberger，Volker Kuhn（作），张宗橙（译）.Coding theory：algorithms，architectures and applications[M].人民邮电出版社，2009.