理论力学运动学关键概念和知识体系梳理

何尚文，张 旭，苗同臣

(郑州大学 力学与工程科学学院，河南 郑州 450001)

理论力学运动学关键概念和知识体系梳理

何尚文，张 旭，苗同臣

(郑州大学 力学与工程科学学院，河南 郑州 450001)

总结理论力学运动学教学中的问题和经验，通过数学基础引入梳理运动学关键概念及点的运动学与刚体运动学的逻辑联系，建立运动学新知识体系，为理论力学运动学教学和教材改革提供参考。

运动学；知识体系；教学、教材改革

Abstract：The teaching problems and experiences of kinematics in theoretical mechanics is summarized. we tease out the key concept and logical relation of particle kinematics and rigid body kinematics by introducing mathematics, and then establish the new knowledge hierarchy. we show that these will provide an effective reference for the teaching and textbook reform in theoretical mechanics.

Key words：kinematics; knowledge system; reform of teaching and textbook

1 引言

运动学联系静力学、动力学，是动力学重要基础。目前运动学教学还存在数学基础引入不够，部分概念抽象、内涵不易理解，点和刚体运动学逻辑关系不够清晰等问题。洪嘉振等[1-2]等指出了运动学教学中存在的问题并探索了新的知识体系；哈尔滨工业大学理论力学教研室教材[3]将刚体平面运动放在点复合运动之后；教材[4]将点的运动学和刚体运动学分开介绍，杜茂林[5]等研究了矩阵法求解运动学问题。本文结合理论力学教学实践，通过引入相关数学基础对运动学关键概念进行解析，对点的运动学与刚体运动学的逻辑联系深入探讨，探索建立了运动学知识新的教学体系，为理论力学运动学课堂教学及教材改革提供参考。

2 运动学关键概念及逻辑关联

2.1 从矢量求导谈速度和加速度的定义

运动定义：点相对于参考系位置随时间的变化。理论力学运动学建立在绝对静止参考系存在的假定下，相对于静(动)坐标系的运动为绝对(相对)运动，绝对(相对)矢径定义：从静(动)参考系坐标原点指向动点的矢量。

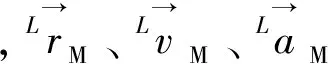
(1)

(2)

式(2)上、下分别表示点相对参考系的速度与加速度。则速度：点相对于参考系的矢径相对于该参考系的导数；加速度：点相对于参考系的矢径相对于该参考系的二阶导数。绝对(相对)速度、绝对(相对)加速度等概念均包含其中。

点相对于点与参考系的速度(加速度)的联系和区别。定义1、2分别为静、动参考系，点N相对于点M的速度为：

(3)

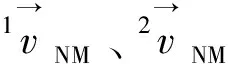
2.2 从泊桑公式的推广谈基点法

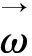
(4)

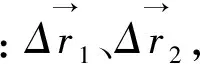
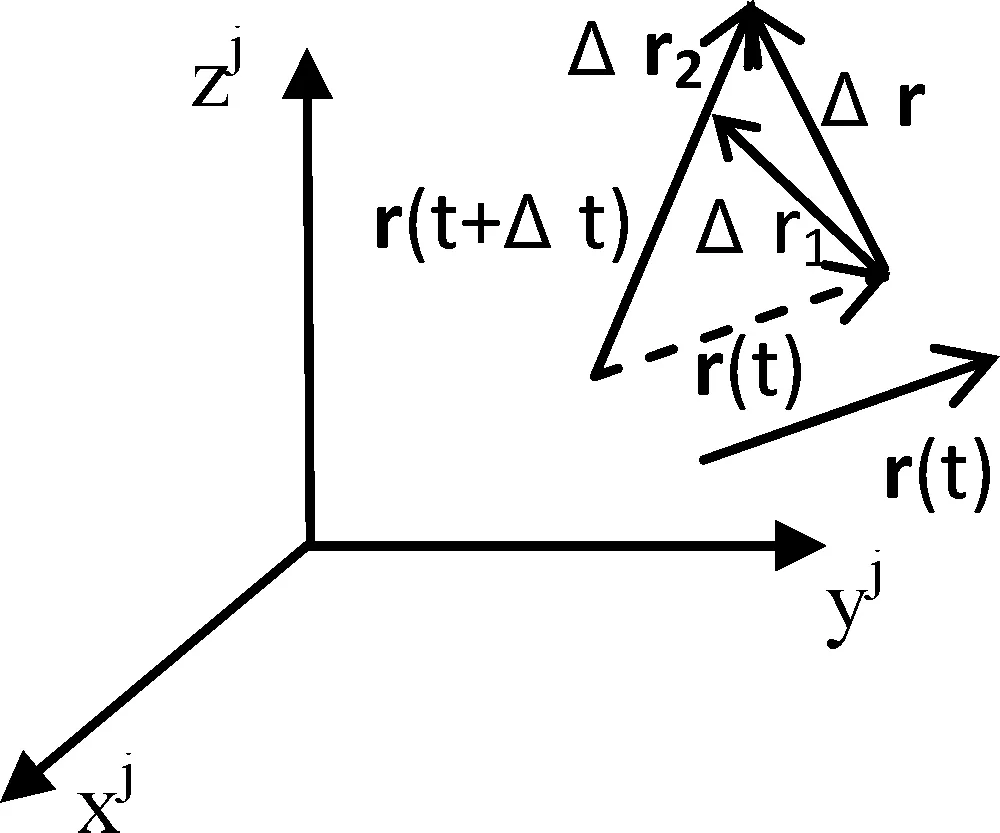
图1 t与t+Δt时刻矢量的位置

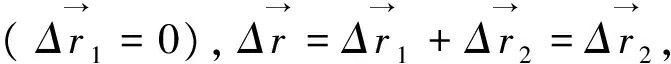
(5)

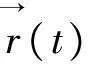
(6)

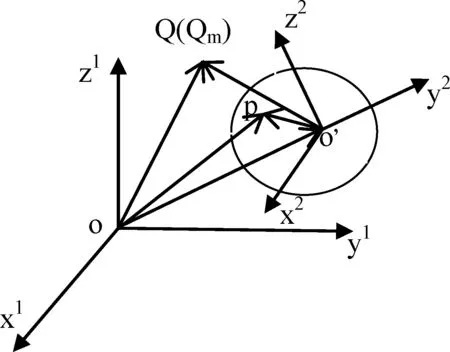
图2 基点法与点的运动合成

图2，动系2固连于刚体，p为刚体上任意点，o,为基点，本文将绝对速度简称为速度，则：

(7)

2.3 从基点法和矢量在不同参考系下求导的关系推导点的运动合成

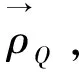
(11)

点的速度及加速度合成定理得证；赋予牵连速度(加速度)物理含义：基点法求出的运动刚体(动系)上定点的速度(加速度)，即Qm相对基点平移参考系的速度(加速度)与基点速度(加速度)的合成；赋予动系物理含义：任意运动刚体。显然式(10)、(11)还可推广至相对不同动系运动的合成。

3 运动学知识体系梳理

综上，在式(2)、(6)基础上可推导整个运动学知识体系。通过数学引入，梳理运动学关键概念及知识间逻辑联系，构建了运动学新知识体系，如图3所示。

数学基础引入包括两部分，一是矢量求导的定义，二是泊桑公式的推广得到矢量在不同参考系下求导的关系。由矢量求导的定义引出速度、加速度的定义，相对速度(加速度)与绝对速度(加速度)具有类似的数学表达形式，使其内涵易于理解，并可由矢量法(直角坐标法和自然坐标法)研究点的运动学。通过泊桑公式推广导出矢量在不同参考系下求导的关系，进而得到基点法并以此研究刚体的运动学；选择运动的刚体为动系使动系不再抽象，且相对运动不再局限为平动和定轴转动(任意运动均可)，基点法求出的刚体上点的速度(加速度)即为牵连速度(加速度)，牵连速度(加速度)为运动刚体上点(选其为基点)的速度(加速度)。最后结合绝对速度(加速度)、相对速度(加速度)、牵连速度(加速度)的定义，由基点法和不同参考系下矢量求导的关系得到点的合成运动规律。

新的知识体系建立在关键概念内涵阐释与数学表达式相对应的基础上，具有概念清晰、逻辑有序、可拓展性好的特点，目前在运动学教学实践中已有良好效果。

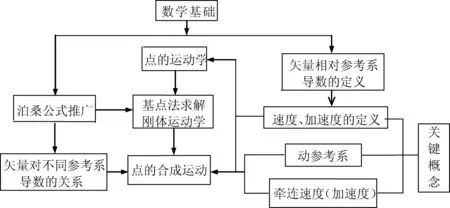
图3 运动学新知识体系

4 小结

本文通过引入相关数学基础阐释了理论力学运动学关键概念的内涵，梳理了知识点之间的逻辑关联，构建了新的运动学教学内容知识体系，为教学、教材改革提供参考。

[1] 洪嘉振，杨长俊.工科理论力学教学体系改革的探索与实践[J]. 力学与实践,1999,6(21)：55-57.

[2] 洪嘉振,刘铸永,杨长俊.理论力学(第四版)[M]. 北京:高等教育出版社, 2015.

[3] 哈尔滨工业大学理论力学教研室.理论力学(第7版)[M]. 北京:高等教育出版社, 2009.

[4] 谢传锋,王琪.理论力学[M]. 北京:高等教育出版社,2009.

[5] 杜茂林,谈志高.运动学中的矩阵方法[J]. 力学与实践,2005,1(27)：69-70.

[6] 周又和.理论力学[M]. 北京:高等教育出版社,2015.

[7] 刘延柱,杨海兴,朱本华.理论力学(第二版)[M]. 北京:高等教育出版社,2000.

Teasing out the key concept and knowledge system of kinematics in theoretical mechanics

HeShang-wen,ZhangXu,MiaoTong-chen

(School of Mechanics & Engineering Science, Zhengzhou University, Zhengzhou 450001,China)

2017-05-15.

何尚文(1983-)，博士，副教授，E-mail:hsw2013@zzu.edu.cn.

国家自然科学基金(51405452);2017郑州大学力学与工程科学学院教学项目资助.

2095-7386(2017)03-0101-03

10.3969/j.issn.2095-7386.2017.03.020

0312.2；G420

A