新弱化缓冲算子的构造与应用
尚运动,朱小林
新弱化缓冲算子的构造与应用
尚运动1,朱小林2
(1.上海海事大学经济管理学院,上海 201306;2.上海海事大学文理学院,上海 201306)
在前人研究的基础之上提出了一类新的弱化缓冲算子来减缓冲击扰动的影响。新构造的弱化缓冲算子是根据统计学思想的几何平均数、调和平均数、平方平均数而提出来的,把新构造的弱化缓冲算子应用于上海港集装箱吞吐量预测的实例上,通过对弱化之后的数据建立GM(1, 1)模型得到预测结果与前人的方法进行比较后发现,新构造的弱化缓冲算子有更高的精度,具有一定的使用价值。
弱化缓冲算子;冲击扰动;统计学
灰色理论研究的是一些样本量小、信息不完整的系统,它是对已知信息进行提取,充分确切对整个系统进行描述的一种方法[1]。根据灰色系统理论,通过对规律性不强的原始数据进行累加或者累减,可以根据少量的信息来研究事物内部潜在的信息。冲击扰动系统的存在导致了定量预测结果与实际情况相差甚远,所以刘思峰教授为了消除序列冲击扰动提出了缓冲算子的概念和公理系统[2]。
党耀国等学者在文献[3-10]构造了若干个弱化缓冲算子,并对其性质进行了研究,通过他们的研究发现构造的弱化缓冲算子有很强的实用性。本文根据弱化缓冲算子的性质,结合统计学的知识,构造了基于几何平均数、调和平均数、平方平均数的弱化算子,根据构造的弱化算子建立GM(1,1)模型对上海港集装箱吞吐量进行预测,并将预测结果与基于刘思峰提出来的一种弱化算子的结果和陈昌源在文献[11]基于一种弱化算子对上海港集装箱吞吐量预测结果进行比较,来判断所构造的缓冲算子的实用性。
1 GM(1, 1)模型的建立
设时间序列

有个观察值,通过累加生成新序列
则GM(1, 1)模型相应的微分方程为:
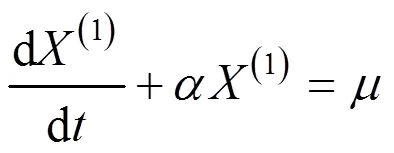
其中:称为发展灰数,称为内生控制灰数。
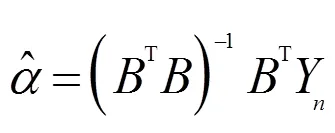
求解微分方程,即可得预测模型:

2 一类新的弱化缓冲算子的构造
首先介绍刘思峰提出的最原始的模型。
设={(1),(2),…,()}是一个有关的时间序列,1={(1)1,(2)1,…,()1}, 其中:
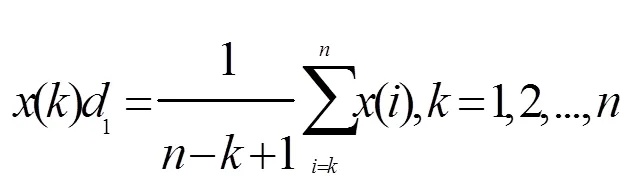
则()1是经过缓冲算子处理之后的序列。
由以上可以看出缓冲算子的实质其实就是一个时刻的数据用该时刻之后的数据来进行调节。在此基础之上,考虑到弱化算子的构造基于平均数的思想,结合统计数的知识,根据几何平均数、调和平均数、平方平均数构造了下面三个缓冲算子。
定理2 设={(1),(2),…,()}是一有关时间序列,且都是大于0的;2={(1)2,(2)2,…,()2}是一经过缓冲算子处理之后的序列,其中所构造的模型为
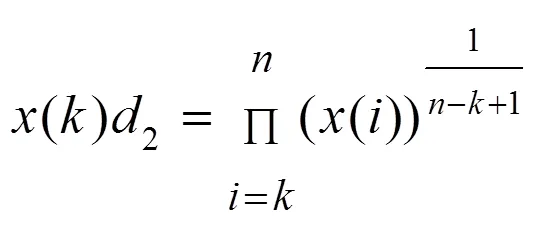
则()2是经过弱化缓冲算子处理之后的数据。
证明 通过计算易得2是符合缓冲算子三公理[12]的,所以2可作为缓冲算子。
(1)设为单调增长序列,则当()≤(),≥≥时
所以
因而2是弱化缓冲算子[12]。
(2)设为单调递减序列,则当()≥(),≥≥k时
所以
因而2是弱化缓冲算子[12]。
(3)当为震荡序列时,设
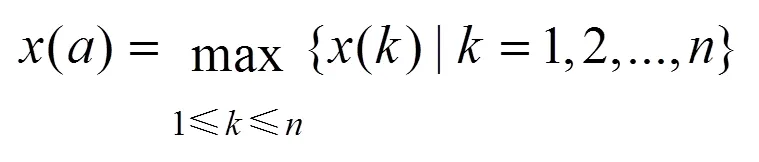
则

即可证

因而2是弱化缓冲算子[12]。
定理3 设={(1),(2),…,()}为相关的时间序列,且都是大于0的数;3=((1)3,(2)3<…,()3}是一缓冲序列,

则()3是经过弱化缓冲算子处理之后的数据,3为弱化缓冲算子,证明同定理2。
定理4 设={(1),(2),…,()}为所研究的时间序列,且每个数都是大于0的;缓冲序列为
4={(1)4,(2)4,…,()4}
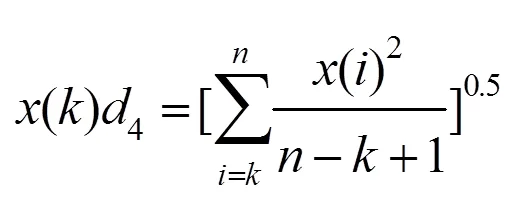
则()4是经过弱化缓冲算子处理之后的数据,4为弱化缓冲算子,证明同定理2。
3 实例验证
近些年来,上海港集装箱吞吐量保持着持续的增长。选取2007~2015年的数据为原始数据,用2007~2014年的数据建模,2015年的数据检验,最后给出2016年的预测值。原始数据和经过各弱化算子弱化之后的数据如表1。对各数据建立GM(1,1)模型,根据模型得到的预测结果如表2。根据表2中得到的数据可以计算绝对相对误差:
绝对相对误差=
是预测值与观测值差值的绝对值与观测值的比值,它测量的是测量值偏离真值的程度,图1反映了各模型绝对相对误差的情况。

表1 上海港集装箱吞吐量有关数据 (万TEU)

表2 根据有关数据建立GM(1,1)模型预测结果 (万TEU)
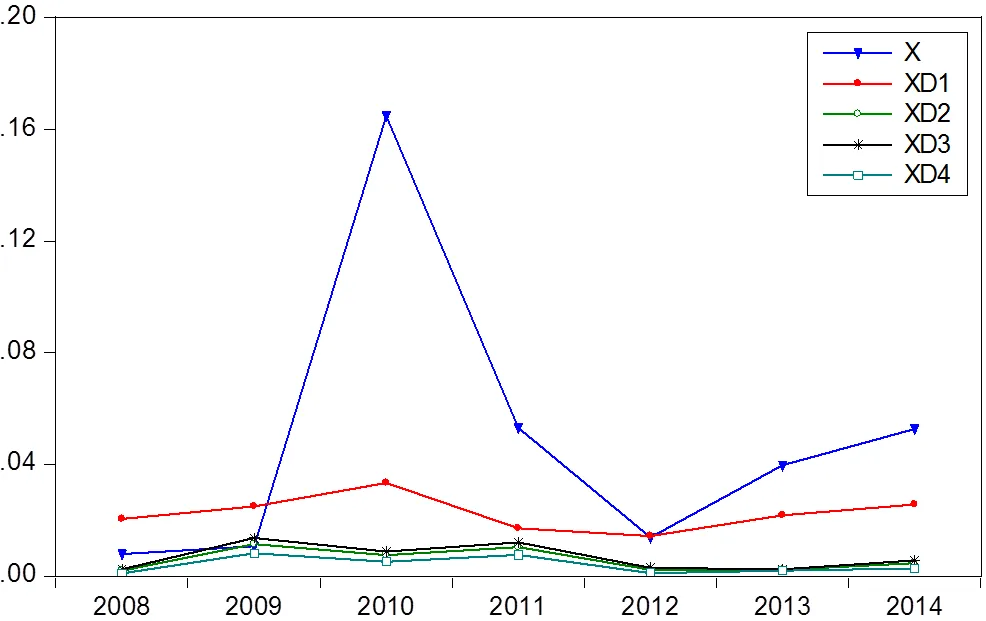
图1 各模型预测结果绝对相对误差图
通过图1可以看出没有经过弱化算子处理的数据建立GM(1, 1)模型的预测结果的绝对相对误差很大,其波动也很大。经过刘思峰建立的弱化算子处理的数据1的预测结果比没有弱化的结果偏离真值的程度要小。但是通过图1可以看出本文新构造的弱化算子处理之后的数据2、3、4预测结果的绝对相对误差要比没有处理的与刘思峰构造的1小,并且波动也不大。表3给出了各模型的平均绝对相对误差和预测误差,从中可以看出经过弱化算子处理之后的平均绝对相对误差要比没有经过处理的要小,本文新构造的弱化算子处理之后的数据2、3、4要比刘思峰构造的1平均绝对相对误差要小。从预测误差上来看,经过弱化算子处理之后的数据建立GM(1,1)的预测误差要比没有处理的要小。
本文新构造的弱化算子处理之后的数据2、3的预测误差比1要小,而4的1.00%的预测误差与1的0.81%比较接近。陈昌源在文献[11]中通过一种弱化算子对上海港集装箱吞吐量进行预测,其预测误差为2.1%,从这一点来看本文构造的新弱化算子都要优于陈昌源的方法。所以综上所述新构造的弱化算子有很强的适用性和实用性,预测精度比较高。
通过新构造的三个弱化算子,分别来预测2016年的上海港集装箱吞吐量,结果如表4。可以取所构造的三个模型的结果的算术平均值作为最终的预测值,所以2016年上海港集装箱吞吐量预测值为3756.38万TEU。

表3 各模型平均绝对相对误差和预测误差

表4 新构造弱化算子2016年预测值 (万TEU)
4 结论
本文结合统计学的思想在已有文献基础上构造了基于几何平均数、调和平均数、平方平均数的一类新的弱化算子,通过弱化算子处理之后的数据建立GM(1,1)模型,可以有效地提高预测的精度。把新构造的弱化算子与已有的弱化算子在上海港集装箱吞吐量上的预测结果进行比较发现本文新构造的弱化算子有更好的准确性与实用性。预测2016年的上海港集装箱吞吐量为3756.38万TEU,这个预测结果可以给港口管理者一个参考,对吞吐量的增长有个定量的把握,更好地应对未来港口的发展。
根据本文所新构造的第三个弱化缓冲算子
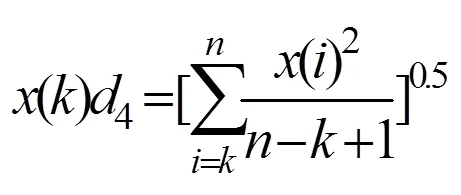
可以将其变形为可调整的算子
其中,取何值时可以达到最优,可以结合神经网络算法、粒子群优化算法等来进行确定,所以这一点可以作为下一步研究的方向。
[1] 刘思峰, 谢乃明. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2008.
[2] 刘思峰. 冲击扰动系统预测陷阱与缓冲算子[J]. 华中理工大学学报, 1997, 25(1): 26-28.
[3] 崔杰, 党耀国. 一类新的弱化缓冲算子的构造及其应用[J]. 控制与决策, 2008, 23(7): 741-744+750.
[4] 姜爱平. 一类弱化缓冲算子的构造及应用[J]. 廊坊师范学院学报: 自然科学版, 2014, 14(6): 17-19.
[5] 刘解放, 刘思峰, 方志耕. 一类调节强度可变的弱化缓冲算子及其应用研究[J]. 中国管理科学, 2016, 24(8): 172-176.
[6] 崔杰, 党耀国, 刘思峰. 基于新弱化算子的GM(1,1)建模精度分析[J]. 系统工程理论与实践, 2009, 29(7): 32-138.
[7] 韩然, 吴正朋, 李梅. 一类新弱化缓冲算子的构造[J]. 中国传媒大学学报: 自然科学版, 2010, 17(4): 57-62.
[8] 刘永菲, 张辉, 解忠诚. 一类新弱化缓冲算子的构造[J]. 中国传媒大学学报: 自然科学版, 2014, 21(3): 51-55+41.
[9] 张苗苗, 燕列雅. 一类新的弱化缓冲算子的拓广及其应用[J]. 陕西科技大学学报: 自然科学版, 2013, 31(1): 165-168.
[10] 强雯, 杨万才. 一种新弱化缓冲算子的构造及应用[J]. 河南科学, 2012, 30(2): 222-226.
[11] 陈昌源, 戴冉, 杨婷婷, 等. 基于改进GM(1,1)模型的上海港集装箱吞吐量预测[J]. 船海工程, 2016, 45(4): 153-156+161.
[12] 党耀国, 刘思峰, 王正新, 等. 灰色预测与决策模型研究[M]. 北京: 科学出版社, 2009.
责任编校:刘亚兵
Construction and Application of New Weakening Buffer Operator
SHANG Yun-dong1, ZHU Xiao-lin2
(1. School of Economics & Management, Shanghai Maritime University, Shanghai 201306, China;2. College of Arts and Sciences, Shanghai Maritime University, Shanghai 201306, China)
A new class of weakening buffer operators is proposed to mitigate the effects of shock perturbations on the basis of previous studies. The new weakening buffer operator is proposed based on the geometric mean, harmonic mean and square mean of the statistical thought. The new weakening buffer operator is applied to the container throughput forecast of Shanghai Port. The GM (1, 1) model is established for the weakened data and the results are compared with those of the predecessors showing that the weakening buffer operator constructed in this paper has higher precision and has certain value in use.
weakening buffer operator; perturbation; statistics
10.15916/j.issn1674-3261.2017.03.017
N94;U691
A
1674-3261(2017)03-0207-04
2017-02-28
国家自然科学基金项目(11301334);上海市科委科研计划项目(14DZ2280200)
尚运动(1991-),男,安徽淮北人,硕士生。朱小林(1975-),男,湖南宁乡人,副教授,博士。

