分数阶统一混沌系统的修正函数投影同步

耿彦峰，王立志，何瑞强



分数阶统一混沌系统的修正函数投影同步

耿彦峰，王立志，何瑞强

（忻州师范学院数学系，山西忻州034000）

对分数阶统一混沌系统的混沌特性进行了分析。当分数阶取某一定值时，系统表现出混沌性态。通过构造适当的响应系统，设计了一种自适应修正函数投影同步的控制方案。选取合适的控制器以及自适应控制率，利用分数阶微分系统的稳定性理论，证明了分数阶误差系统为渐近稳定，进而得出驱动系统和响应系统最终实现自适应修正函数投影同步，且可以对驱动系统的不确定参数进行估计。最后，利用Adams-Bashforth-Moultom算法，对文中的结论进行数值仿真，其结果说明了该方法的有效性和可行性。

分数阶；统一混沌系统；修正函数；投影同步；数值仿真

随着混沌控制同步研究的深入，多种混沌同步的概念被相继提出[1-3]。最近，又有学者提出了一种新的同步-修正函数投影同步[4]，即驱动系统按照期望的函数尺度因子矩阵同步到响应系统。它在工程领域和保密通信中有着非常诱人的应用前景，引起了中外学者的广泛关注[5-7]。

与此同时，大量的分数阶混沌系统如分数阶Chua电路、分数阶Chen系统和分数阶Lorenz系统等不断被证明存在。随之，分数阶混沌系统的控制与同步就成为混沌学新的研究课题，并取得了很多研究成果[8-10]。2002年，由吕金虎等[11]提出了统一混沌系统。由于统一混沌系统具有更广泛的意义和研究价值，故很多学者对其进行研究，并取得了一些研究成果[12]。但是，对于分数阶统一混沌系统的修正函数投影同步的研究成果却并不多见。

为此，本文对于分数阶统一混沌系统的自适应修正函数投影同步问题进行研究。基于分数阶微分系统的稳定性理论及混沌控制同步的相关机理，通过构造响应系统和设计合理的控制器，并选取合适的控制率；最终，实现了自适应修正函数投影同步的控制目的，并可对驱动系统的不确定参数进行估计。最后，文章给出具体实例的数值仿真，验证了所设计的控制方案的正确性和有效性。

1 准备知识

文献[13]在研究分数阶微积分时，对微分和积分的概念提出了几种定义。由于Caputo定义的初始条件有明确的物理意义，所以本文采用的是Caputo定义[13]。

定义1[4]对于混沌系统和，若存在函数对角矩阵使得：

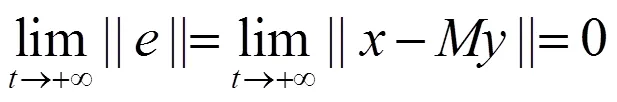
引理1[10]对于分数阶系统≤，如果存在正定阵使函数≤0恒成立，则系统为渐近稳定的。

考虑具有如下形式的统一混沌系统：

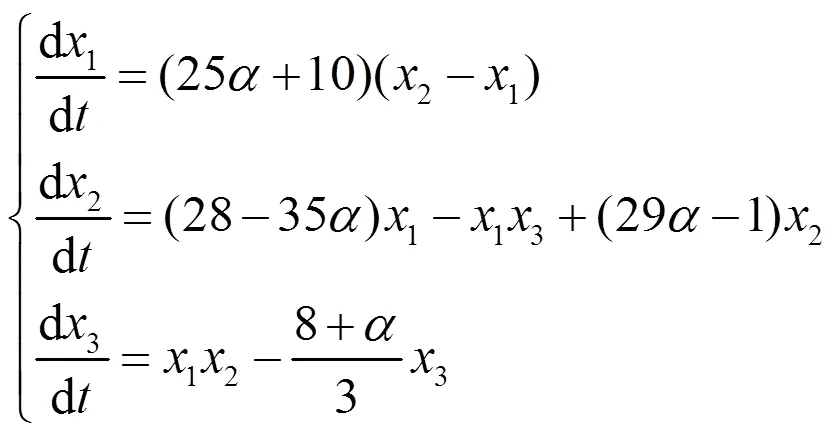
系统(2)相应的分数阶系统为：

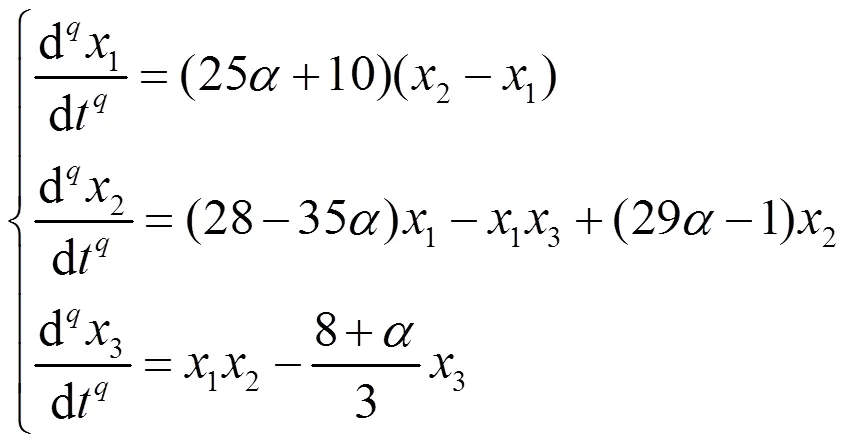
2 主要结果

系统(3)用矩阵的形式可表示为：

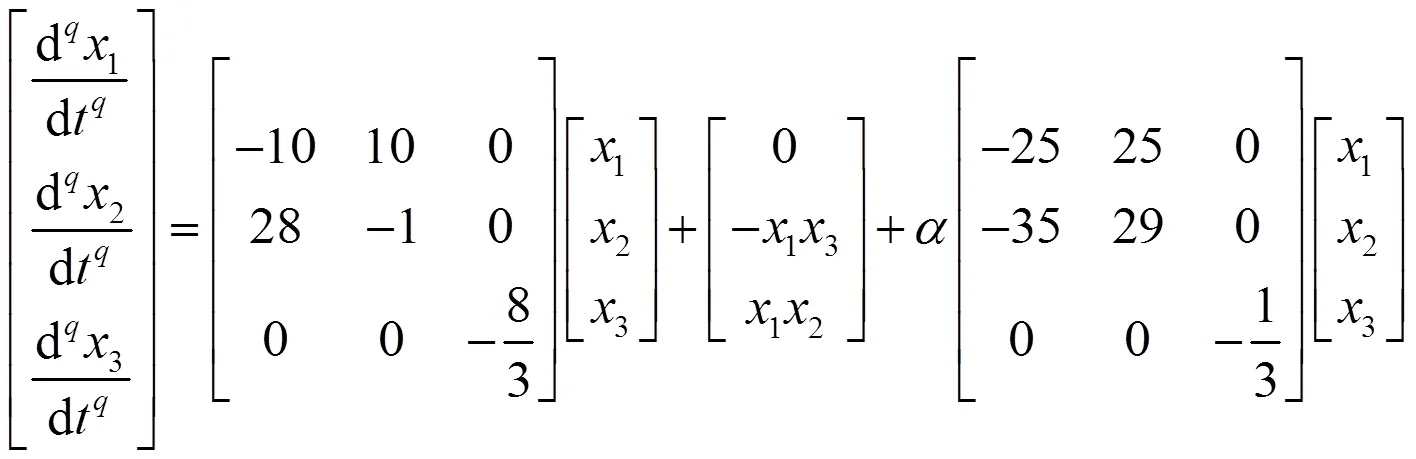
即可写为如下形式的混沌系统：

(5)

将系统(5)作为驱动系统，构造具有如下形式的响应系统：

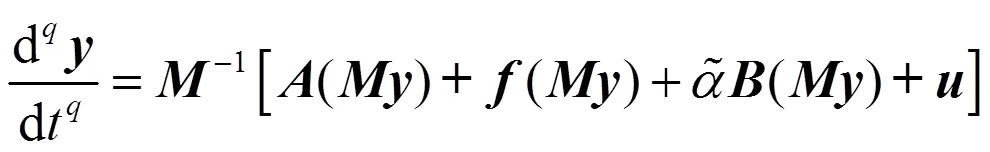
(7)

则误差系统为：

(8)

设计自适应控制器为：

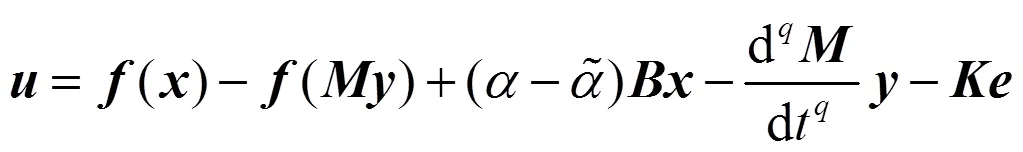
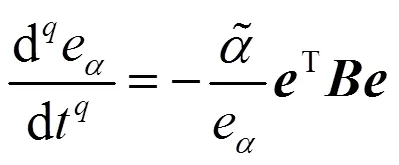
定理1 对于驱动系统(5)和响应系统(6)，若采用控制器(9)及自适应律(10)；并选取，使得为负定阵，则分数阶系统(5)和(6)可按误差式(1)实现自适应修正函数投影同步。

证明 由定理构造函数为：

将式(8)、(9)、(10)依次代入式(11)，可得：

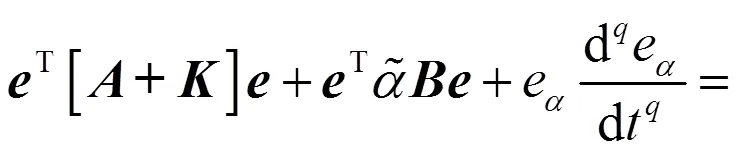
由引理1可知，误差系统式(8)是渐近稳定的，即在控制器(9)和自适应律(10)的作用下，驱动系统(5)和响应系统(6)可实现自适应修正函数投影同步。证毕。

3 实例仿真

为了验证上述控制同步方法的正确性和有效性，在下面实例仿真中，采用了Adams-Bashforth-Moultom算法，进行数值仿真。

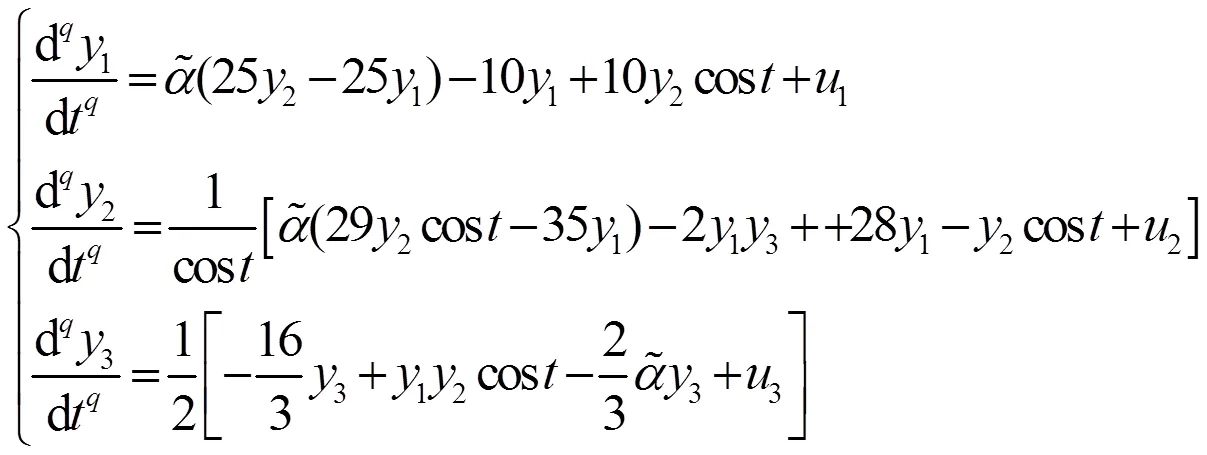
(13)

自适应控制率取为：

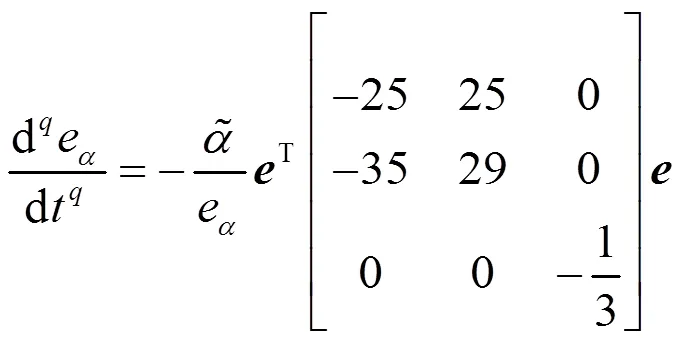
图2 ()-曲线

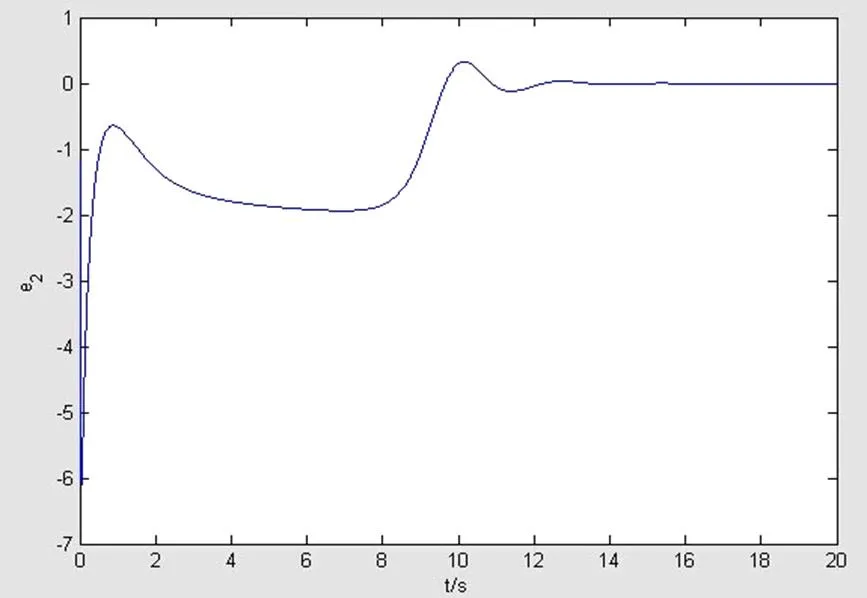
图3 e2(t)-t曲线

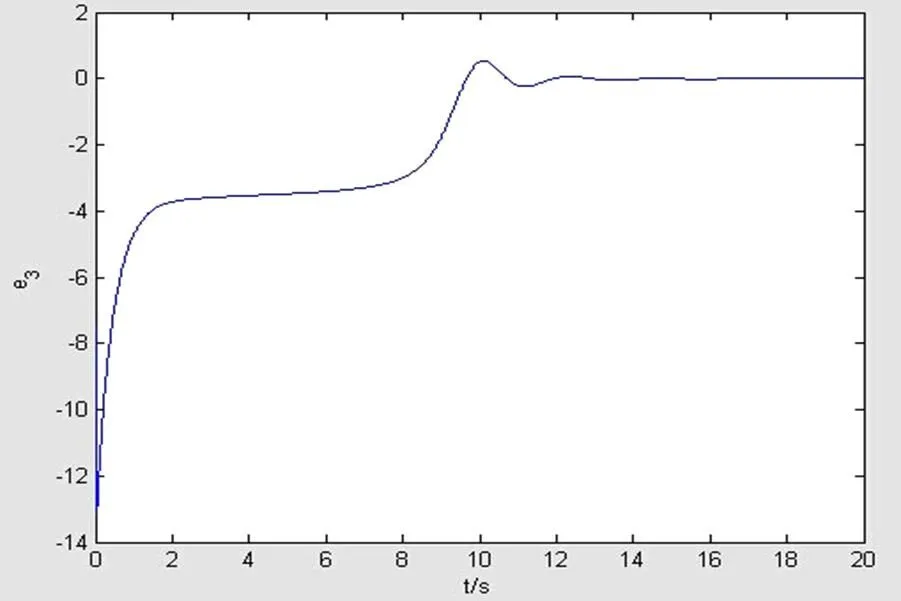
图4 e3(t)-t曲线

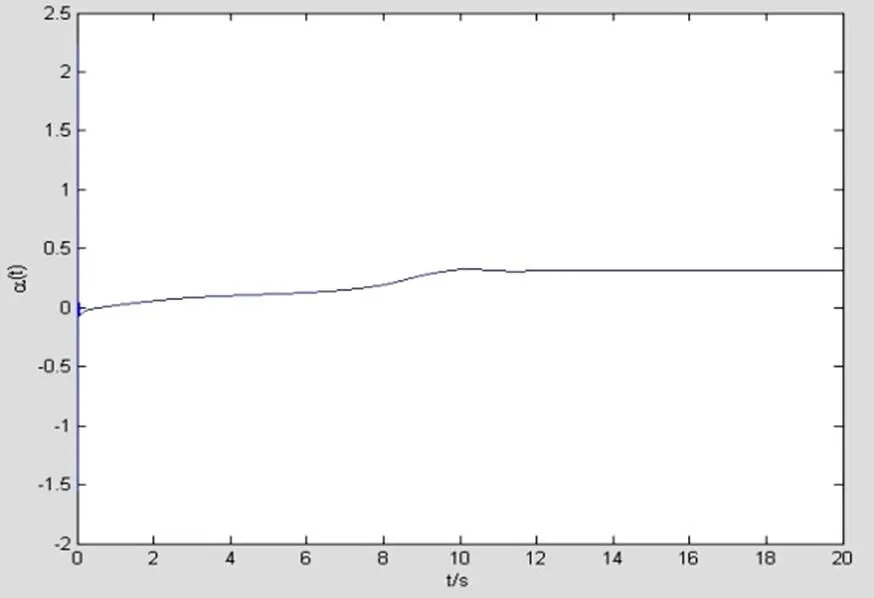
图5 (t)-t曲线

4 结束语

本文对于具有不确定单参数的分数阶统一混沌系统，通过构造响应系统，并对系统的未知参数引入自适应控制率，最终实现了混沌控制同步。所设计方法简单易行，控制方案论证较为严密，且能通过自适应律自动调整以跟随系统参数的变化，因而具有较强的鲁棒性。由于修正函数投影同步是一种更广义的同步，有着更广泛的应用。因此，本文的研究结果在工程领域中，尤其是保密通信中提供了理论依据。

[1] Huang Tingwen, Li Chuangdong, Liu Xinzhi. Synchronization of chatic systems with delay using intermittent linear state feedback[J]. Chaos: Interdisciplinary J Nonlinear Sci, 2008,18(3): 1-8.

[2] 耿彦峰, 蹇继贵, 张炎彪. 一类互联电力系统的部分联结稳定性分析[J].江西理工大学学报: 自然科学版, 2013, 34(3): 67-70.

[3] Wu Quanjun, Zhou Jin, Xiang Lan, et al. Impulsive control and synchionizationofchaotic Hindmarsh-Rose models for neuronal activity[J]. Chaos, Solitons and Fractals, 2009, 41(5): 2706-2715.

[4] Du H Y, Zeng Q S,Wang C H. Modified function projective synchronization of chaotic systems[J]. Chaos, Solitons & Fractals, 2009, 42(4): 2399-2404.

[5] Yu Y G, Li H X. Adaptive generalized function projective synchronization of uncertain chaotic systems[J]. Nonlinear Analysis: Real World Applications, 2010, 11(4): 2456-2464.

[6] 方洁, 胡智宏, 江泳. 耦合混沌系统自适应修正函数投影同步[J]. 信息与控制, 2013, 42(1): 39-45.

[7] Sudheer K S, Sabir M. Adaptive modified function projective synchronization between hyperchaotic Lorenz system and hyperchaotic Lu system with uncertain parameters[J]. Physics Letters A, 2009, 373(41): 3743-3748.

[8] 刘杰, 李新杰, 何小亚, 等. 分数阶超混沌系统的线性广义同步观测器设计[J]. 动力学与控制学报, 2009, 7(3): 245-251.

[9] 张广军, 董俊, 姚宏, 等. 分数阶Chen混沌系统的完全同步与反相同步[J]. 应用力学学报, 2013, 30(2): 201-206.

[10] 孙克辉, 杨静利, 丘水生. 分数阶混沌系统的仿真方法研究[J]. 系统仿真学报, 2011, 23(11): 2361-2370.

[11] Lü Jinhu, Chen Guanrong, Zhang Suochun. A unified chaotic system and it’s research[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2003, 20(1): 123-129.

[12] 张若洵, 杨洋, 杨世平. 分数阶统一混沌系统的自适应同步[J]. 物理学报, 2009, 58(9): 6039-6044.

[13] Podlubny I. Fractional differential equations[M]. New York: Academic Press, 1999. 责任编校：孙 林

Modified Function Projective Synchronization of the Fractional-order United Chaotic System

GENG Yan-feng, WANG Li-zhi, HE Rui-qiang

（Department of Mathematics, Xinzhou Teachers University, Xinzhou 034000 China）

For the fractional-order united chaotic system, the chaos behavior is displayed when the fractional-order is used as certain fixed values in this paper. A controlling scheme of adaptive modified function projective synchronization about the united chaotic system is designed by structuring a suitable response system. By means of stability theory of the fractional-order differential systems, it is proved that the zero solution of the error system is asymptotically stable by choosing appropriate controller and adaptive law. Accordingly, it is concluded that master system and response system arrive at adaptive modified function projective synchronization, and the uncertain parameters of master system could be estimated. Finally, an illustrative example with simulations via Adams-Bashforth-Moultom algorithm is used to demonstrate the validity and feasibility of the proposed results.

fractional-order; Chen chaotic system; modified function; projective synchronization;numerical simulation

10.15916/j.issn1674-3261.2017.03.016

O193

A

1674-3261(2017)03-0202-05

2016-12-14

耿彦峰（1979-），男，山西大同人，讲师，硕士。