温度影响下主缆线形精细计算方法研究与应用

(湖南交通国际经济工程合作有限公司， 湖南 长沙 410004)

温度影响下主缆线形精细计算方法研究与应用

钟阔

(湖南交通国际经济工程合作有限公司， 湖南 长沙 410004)

悬索桥施工前，应通过基于有限元方法的杆件正向装配及逆向拆除法来进行正反向计算，若2种计算得到的成桥状态各项数据闭合且合理，则可基于此确定其各项施工参数。但上述计算是基于设计基准温度，而施工时环境温度与设计基准温度存在差异，且主缆索股的垂度与线形受温度影响较大，上述2种温度的差异使得主缆架设完成时其空缆线形参数与理论值不一致。因此，在施工前及施工过程中应根据2种温度的差异对主缆形状的影响规律来调整空缆状态下主缆的线形。为此在悬索桥施工过程主缆线形的解析计算方法基础上，推导了2种温度影响下主缆形状计算表达式，并编写成数值计算程序用于主缆施工控制过程中，能保证施工完成时桥梁处于合理成桥状态，本计算方法也可用于其他悬索桥的主缆施工过程中。结合大跨径地锚式悬索桥算例，验证了悬索桥主缆施工过程中考虑温度因素的空缆线形计算方法的正确性。

悬索桥； 温度作用； 设计基准温度； 非设计标准温度； 主缆线形

0 引言

大跨径悬索桥结构计算一般采用有限单元方法和恒载作用下的解析迭代计算法[1]。前者通过倒拆法与正装计算方法相结合来寻找结构的各种合理状态。后者则以主缆在任意时刻的无应力总长保持恒定的原理来进行其施工过程及成桥各个状态的计算[2,3]。

悬索桥计算过程中一般先通过合理的成桥状态进行杆件逆向拆除分析法得到各个构件的施工初始状态，而后进行杆件的正向装配计算得到相应成桥状态。若此计算成桥终态与初拟桥梁成桥状态相一致，则可基于计算得到的各项桥梁初始状态数据进行主缆及吊杆系统的下料与施工。但上述倒拆和正装分析所得到的各项施工参数都是基于设计基准温度，而施工时缆索并不是处于设计基准温度，且温度对索股垂度与线形的影响较大，环境温度与设计基准温度的差异可使主塔、索鞍及主缆本身产生变形与变位，从而导致架设完成的主缆形状与理论值不一致[4-7]。基于此，在施工中应根据温度对空缆状态下主缆的形状参数进行适当地调整。本文在主缆找形的2种计算理论(抛物线及悬链线理论)基础上，推导了主缆受温度影响的线形计算表达式，并将程序计算结果用于实际施工过程中。本文方法下的悬索桥计算及施工结果表明，考虑温度对主缆线形影响的计算方法能符合主缆施工的实际情况，将非标温度主缆线形状态的理论计算结果用于施工，能保证安装索夹、吊杆、吊装加劲梁以及施工桥面系后桥梁处于合理的成桥状态。本文考虑温度对主缆线形影响的计算方法也可在其他同类型桥梁的主缆施工过程中得到应用。

1 主缆索股的温度分布模型

1.1 主缆各索股温度的分布模式

本文考虑将组成主缆各索股的平均温度值作为其温度值。主缆温度测试过程中，先通过安装在主缆各索股上的温度传感器得到其测温结果，然后基于实测的各个索股的温度通过计算得到主缆内侧索股温度T(n)和外侧索股温度T(w)的平均值，T(n)与T(w)的关系可用下式表示[8]：

T(n)=T(w)+a

(1)

假定上式中a沿主缆纵桥延伸方向为恒定值，则不同主缆断面的温度可按下式求得：

T=∑(T(w)i+a)/n

(2)

式中:n为外侧主缆索股测温点总数。

主缆内外温差受环境(气温与风力)因素影响大。主缆在夜间的内外温差取决于白天的天气情况(白天气温高时，夜间主缆内外温差稍大，反之，则温差小)。此外，自然风力大小也可造成主缆内外温差的不同。因此每次测温时，应注意在同一时间进行特设的主缆断面各个索温的测试，并通过测试得到的温度算得a值，其他位置的主缆则只需测定其外侧的温度即可。根据特定断面索温算得的a值，可求得任意主缆断面的温度。

1.2 主缆温度沿其纵桥延伸方向的分布模式

温度沿主缆纵桥向分布的函数T(x) (x为主缆纵桥向坐标)可表示如下：

Ti(xi)=kixi+bi

(3)

式中：i为测试断面间索段数；k为本段内线性函数的斜率；b为本段内线性函数的截距。

2 考虑温度影响的2种线形计算方法

2.1 温度影响下的主缆线形简化计算方法

本节温度影响下主缆线形简化计算方法是基于抛物线找形计算方法。

施工中，温度变化对主缆索股的几何线形变化影响大。施工中应根据实时环境温度对主缆的控制性设计参数进行适当调整。针对温度变化对索股跨中标高进行调整时，一般认为同一跨主缆为同一温度，主缆在温度影响下的伸长量为：

ΔSt=αSo(T-20)=αSoΔT

(4)

式中：α为线膨胀系数；T为断面平均温度；20为标准温度,℃；So为索的无应力长度。

从几何角度分析可知，主缆索长产生ΔSt的改变时其垂度将产生Δf的改变，主缆内力也随垂度的改变而改变。由材料力学可知，内力的变化又将导致主缆有相应的伸长量的变化，反过来又重新影响主缆索股的垂度。但工程中精度能满足要求的情况下，可忽略上述变化。因此，索股长度变化的ΔSt引起的主缆垂度变化的Δf就可作为温度影响下主缆的线形调整量。ΔSt与Δf之间可表达为线性关系：

ΔSt=βΔf

(5)

若令n为索股的垂跨比：n=f/L，则上式中的β可表达如下：

(6)

(7)

其中θ为边跨倾角。β值的推导依据为计算悬索桥线形及内力状态的抛物线理论[5,6]，下文将简要阐述中跨β值的推导思路。在主缆垂度与跨度的比值较小时，可认为中跨主缆在恒载作用下呈抛物线形状，如图1，其方程为：

(8)

则可得到下述抛物线理论下主缆的简化弧长计算公式，将其进行级数展开，考虑到线形计算在满足工程精度的前提下应尽量简化，故取展开式的前2项，弧长表达式为：

(9)

所以：

(10)

图1 两端等高索段的计算图示

根据式(6)、式(7)算得β后，ΔSt与Δf之间的关系如式(10)，由此，垂度改变量df与温度改变量ΔT之间的关系可线性表示为：

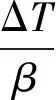
(11)

如上所述，只需求得αSo/β(单位温差作用下主缆的垂度改变)，即可算出其它温度作用下的主缆垂度改变量Δf。

但是上文提到了，主缆索长变化ΔSt、垂度变化Δf及内力变化的相互影响关系。可见主缆长度与垂度之间的相互影响呈现出非线性的性质。悬索桥主塔顶的标高与塔偏也会随温度改变而产生相应改变，进而也将影响主缆的状态[9]。并且主缆全跨也并非统一温度，故将主缆全跨视为统一温度也将给计算带来误差。

因此，需要找到其他更加精准的主缆温度分布模式和更完善的计算方法，来求解主缆在温度作用下的线形与内力状态。

2.2 温度影响下主缆线形的迭代计算方法

本节温度影响下主缆线形计算方法是基于主缆找形的悬链线计算理论。由主缆索股温度沿桥梁纵向分布的关系式Ti(xi)=kixi+bi，温差作用下的主缆的弹性伸长为：

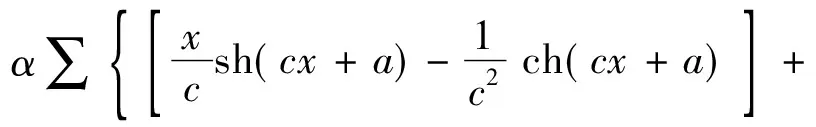
(12)

式中：a为积分后得到的积分常数，其求解过程可参见文献[9]；α为主缆材料的线膨胀系数；t为设计基准温度值，一般取值为20 ℃。

基于任何情况下主缆的自然状态长度(主缆内无拉应力)为定值的前提条件，基准温度下主缆在恒载作用下的弹性总长为：

S=S0+ΔSH+ΔSt

(13)

式中：S0为主缆无应力长度；ΔSt为温差引起的主缆伸长量；ΔSH为主缆拉力引起的弹性伸长。

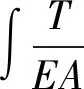
(14)

中、边跨主缆的有应力总长可表达为：

中跨：S′=2sh(cL/2)/c

(15)

(16)

同时可以得到主缆在有应力状态下的垂度表达式为：

( 17)

(18)

显然，由式(13)及式(15)、式(16)表达的2种主缆总长应相等。故有S=S′这个非线性方程组。通过数值迭代计算，可算得参数c。以中跨主缆为例，求解步骤为：

1) 先假定c1=q/H，计算出:

S=S0+ΔSH+ΔSt;

2) 根据ci=2sh-1(Sci-1/2)/L由此计算出ci，再将ci代回S′=2sh(cL/2)/c得到S′;

4) 将前述步骤计算得到的ci值，代入式(13)中，算得S，将S代入第2、第3步计算得cj；

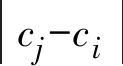
将上述迭代计算流程算得的主缆悬链线理论下的参数c值代入式(15)、式(16)，再结合式(17)、式(18)式可算得温度影响下的主缆垂度的调整量。

3 温度影响下主缆线形的2种计算方法及其在实际应用中的比较

3.1 工程概况

本工程背景为张花高速公路上某单跨地锚式悬索桥，整体桥梁结构布置为双塔双索面跨径，主缆跨径组成为(200+856+190)m。主缆架设完成时，在自重作用下，中跨主缆的垂度f=77.3 m，其垂度与跨度的比值为1∶11.1；2个边跨的布置基本对称,边跨主缆在空缆状态下垂度与跨度之比约为1∶59.66。运用分段悬链线数值迭代计算方法求得主缆无应力状态下的长度为：张家界侧边跨为Lz=222.520 m ，Lm=874.660 m ，Lh=212.179 m，其中Lz、Lm及Lh表示为起点(张家界)侧边跨、中跨及终点(花垣)侧边跨主缆在自然状态下的长度。悬索桥空缆状态下结构如图2。

图2 某大跨径悬索桥空缆状态下结构图示(单位： m)

3.2 温度影响下的主缆线形计算结果

恒载及温度影响下中跨主缆垂度计算结果见表1、图3。

表1 恒载及温度影响下中跨主缆垂度计算结果温度/℃基于抛物线理论的简化计算方法基于悬链线理论的迭代计算方法中跨主缆跨中标高/m中跨垂度调整量/m中跨主缆跨中标高/m中跨垂度调整量/m-5520693-0109520699-0115-4520671-0087520675-0091-3520650-0066520652-0068-2520628-0044520629-0045-1520606-0022520606-0022052058400005205840000152056200225205620022252054000445205390045352051800665205160068452049700875204930091552047501095204690115

图3 恒载及温度影响下中跨主缆垂度计算结果比较图

4 结语

1) 本文在简述悬索桥施工的基本计算与控制方法基础上，指出了考虑施工过程实时环境温度对架设过程中主缆(索股)线形影响的必要性。

2) 基于悬索桥2种主缆找形理论(传统抛物线理论及悬链线计算理论)分别推导了考虑温度影响的主缆线形简化计算与精细迭代计算公式及主缆线形调整公式，编写了基于温度影响的主缆线形计算程序并将其用于悬索桥空缆架设过程监控计算中。

3) 施工过程中，基于理论计算结果得到的非标温度下的主缆线形状态结合本文的线形调整方法能保证安装索夹、吊杆、吊装加劲梁等各项工序后结构处于合理的成桥状态，这表明本文提出的温度影响下的悬索桥主缆施工架设线形控制方法是合理可行的。

4) 本文提出的基于温度影响下的悬索桥主缆线形计算方法也可用于其他悬索桥的主缆施工过程中，为悬索桥主缆的架设过程提供了考虑温度的索股线形调整的2种实用计算方法。

[1] 贺拴海. 桥梁结构理论与计算方法[M].北京:人民交通出版社，2003.

[2] 黄平明,梅葵花,徐岳. 大跨径悬索桥主缆系统施工控制计算[J]. 西安公路交通大学学报,2000(4):19-22.

[3] 李传习,任亮,刘光栋,等.大跨度悬索桥架设参数迭代计算方法探讨[J].桥梁建设,2004(6):31-34,58.

[4] 李传习,王雷,刘光栋,等.悬索桥索鞍位置的分离计算法[J]. 中国公路学报,2005(1):67-72.

[5] 唐茂林,沈锐利,强士中. 大跨度悬索桥丝股架设线形计算的精确方法[J]. 西南交通大学学报,2001(3):303-307.

[6] 沈锐利. 悬索桥主缆系统设计及架设计算方法研究[J]. 土木工程学报,1996(2):3-9.

[7] 梅葵花. 悬索桥主缆温度效应的分析研究[A]. 中国公路学会桥梁和结构工程分会、重庆市交通委员会.中国公路学会桥梁和结构工程学会2001年桥梁学术讨论会论文集[C].2001.

[8] 林一宁,余屏孙,林亚超. 悬索桥架设期间主缆温度测试研究[J]. 桥梁建设,1997(3):60-68.

[9] 何为.大跨径悬索桥施工监控中若干问题的研究[D].杭州：浙江大学,2006.

1008-844X(2017)03-0121-04

U 448.25

A

2017-06-30

钟 阔(1987-)，男,工程师,从事公路和与桥梁施工。