K型偏心支撑对钢框架结构抗震性能影响分析

王 淞，雷庆关

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

K型偏心支撑对钢框架结构抗震性能影响分析

王 淞，雷庆关

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

K型偏心支撑弹性阶段刚度大，在地震作用下通过偏心梁端剪切屈服限制支撑受压屈曲。通过SAP2000有限元分析软件，对平面L型不规则钢框架结构在增设K型偏心支撑前的模型一和增设K型偏心支撑后的模型二分别进行模态分析、水平双向反应谱分析和弹性时程分析，得到两个模型的自振周期、质量参与系数、楼层位移和层间位移角。结果表明：K型偏心支撑在提高结构抗扭能力，增强结构抗侧刚度方面作用显著，为今后设计工作提供参考。

抗震性能；偏心支撑；钢框架；模态分析；反应谱分析；时程分析

Abstract： The elastic phase of K-type eccentric support is large, and under the action of earthquake, the compression buckling is restrained by the shear yield of the eccentric beam.Through SAP2000 finite element analysis software, in this paper, the model of the planar L-type irregular steel frame structure before adding K-type eccentric support is analyzed, the modal analysis, the horizontal bidirectional response spectrum analysis and the elastic time-history analysis are carried out respectively, and the self oscillation period, the mass participation coefficient and the two models as well as floor displacement and interlayer displacement angle are obtained. The results show that the K-type eccentric support plays a significant role in improving the torsional ability of the structure and strengthening the lateral stiffness of the structure, which provides reference for the future design work..

Keywords： seismic performance; eccentrical brace; steel frame; modal analysis; response spectrum analysis; time history analysis

当房屋较高时，在水平荷载作用下，结构侧移较大，采用纯框架体系影响正常使用。为了满足要求，往往采用超过承载力设计要求的梁、柱截面，框架梁柱的强度可能有“剩余”没有被充分利用，这是不经济的[1]。 钢框架支撑结构体系是在框架体系中沿结构的纵、横两个方向均匀布置一定数量的支撑所形成的结构体系[2]。偏心支撑框架中的支撑斜杆，应至少有一端与梁连接，并在支撑与梁交点和柱之间或支撑同一跨内另一支撑与梁交点之间形成消能梁段[3]。1977年美国加州大学通过1/3模型框架的试验，首次验证了偏心支撑钢框架优异的抗震性能，随后在美国等西方国家相继将偏心支撑框架用于一些高层建筑作为抗侧力体系的一部分[4]。本文通过大型有限元分析软件SAP2000对一平面L型不规则钢框架结构在增设K型偏心支撑前后的模型进行对比分析，研究结构在平扭振型、自振周期、楼层位移、层间位移角方面的变化，探讨K型偏心支撑在提高钢框架结构抗扭能力和抗侧刚度方面的作用，评估结构抗震性能。

1 建立模型

运用大型有限元分析软件SAP2000对一栋平面L型不规则钢框架结构进行建模分析，结构模型共15层，层高均为3.2 m，总高48 m。横跨和纵跨均为5.8 m，平面呈L型，平面图如图1所示。框架梁采用HM400×300×10×16，框架柱采用HW500×500×15×20，支撑采用HW300×300×10×15，均为Q345级钢。楼板采用100 mm厚C30混凝土现浇板。楼面恒荷载为3.5 kN/m2，活荷载为2.0 kN/m2，边梁线荷载为8 kN/m。本地区采取八度抗震设防，场地类别为Ⅱ类，设计分组为第二组。根据《建筑抗震设计规范》(GB 50011-2010)，因为l/Bmax=17.4m/17.4m=1>0.30，所以判定结构为平面凹凸不规则[5]。模型一不设置支撑，如图2所示；模型二设置K型偏心支撑，如图3所示。

图1结构平面图图2不设置支撑的模型一

图3 设置K型偏心支撑的模型二

2 抗震性能分析

2.1模态分析

结构的模态分析用于确定结构的振型，是结构动力分析的基础。用反应谱振型组合时，需要知道前几阶振型，振型还是后续时程分析中振型叠加的基础[6]。模型一和模型二的前12阶自振周期及质量参与系数分别如表1和表2所示。

表1 模型一前12阶自振周期及质量参与系数

表2 模型二前12阶自振周期及质量参与系数

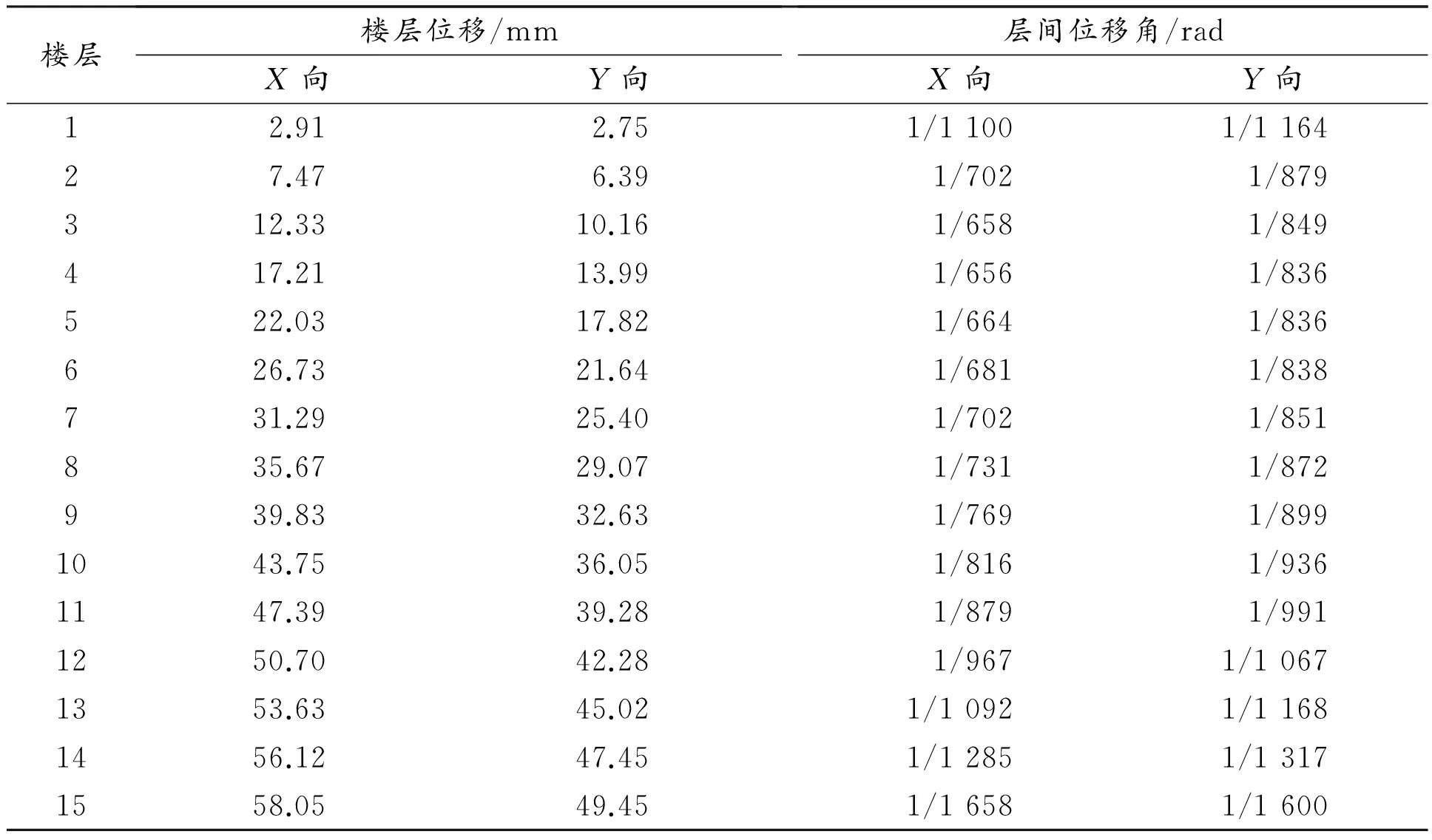
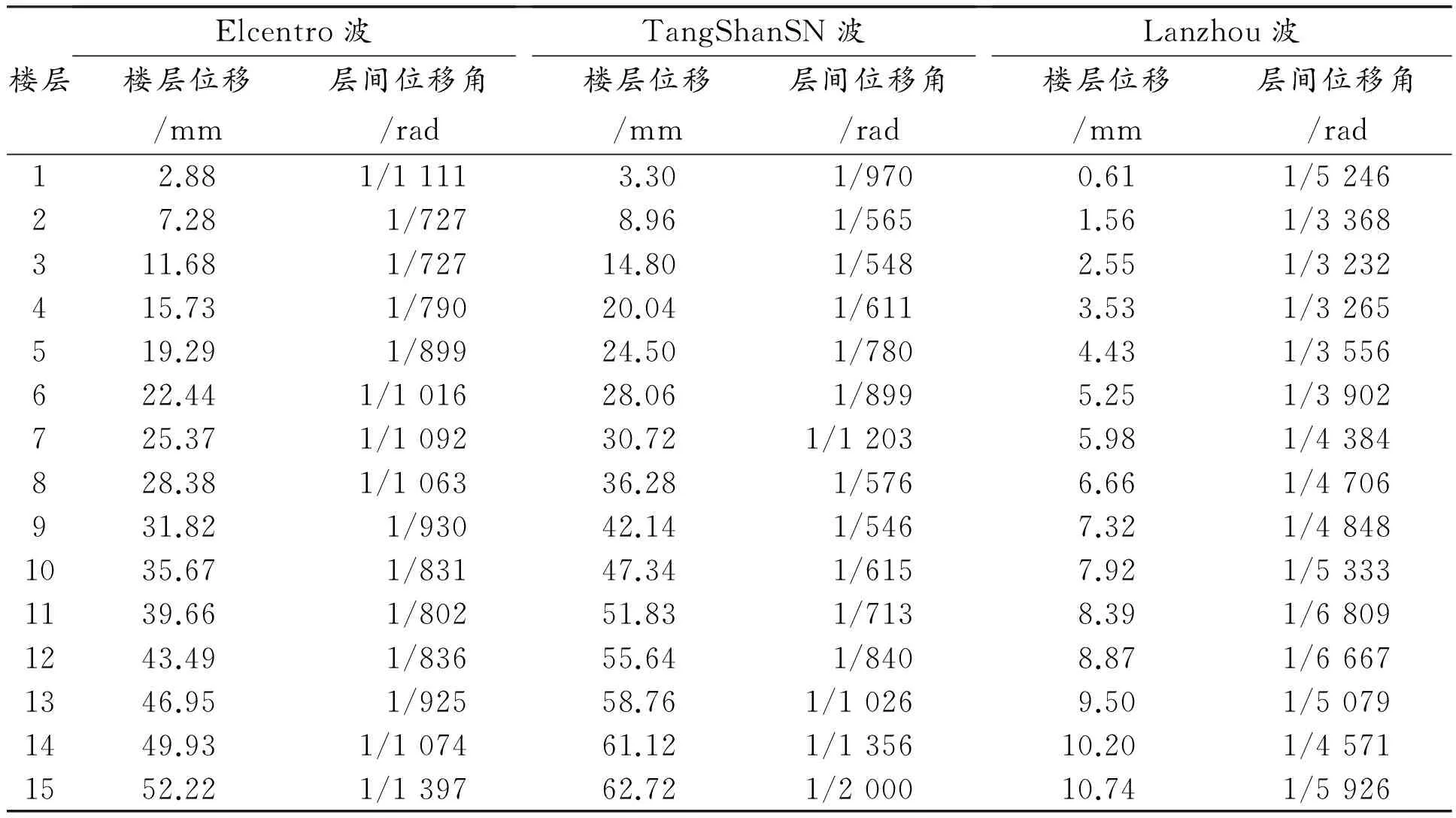
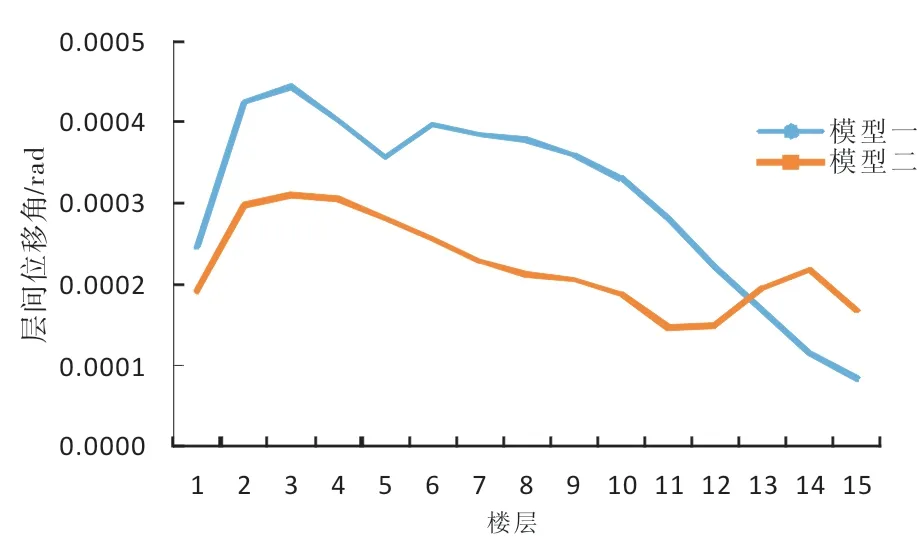
通过质量参与系数判断平扭振型主要比较的是UX、UY和UZ三个自由度质量参与情况。对于模型一，由表1可知：第一振型质量参与系数UY为0.8，UX为0，RZ为0.01，可以判断第一振型为Y方向的平动振型；第二振型中UX为0.18，UY为0，RZ为0.61，RZ>UX+UY,可以判断第二振型为扭转振型，但带有一定的X方向的平动效应；第三振型中UX为0.61，UY为0，RZ为0.19，RZ

《高层建筑混凝土结构技术规程》(JGJ 3-2010)中规定“计算振型数应使各振型参与质量之和不小于总质量的90%”，主要看最后一个阵型输出项中的sumUX和sumUY，这两项分别给出了X和Y方向各振型质量参与系数的累加值。在模型一中sumUX为95%，sumUY为96%；在模型二中sumUX为95%，sumUY为97%，两个模型中的sumUX和sumUY均满足规范要求。

2.2水平双向反应谱分析

反应谱是结构自振周期和阻尼比的函数。地震作用反应谱分析本质上是一种拟动力分析，它首先使用动力方法计算质点地震响应，并使用统计的方法形成反应谱曲线，然后再使用静力方法进行结构分析[7]。反应谱分析计算结构地震反应的优点是计算较简单并且考虑了多个地震运动的激发影响。本结构平面凹凸不规则，质量和刚度分布明显不对称，采用SAP2000对模型一和模型二分别进行水平双向反应谱分析，计算结果如表3和表4所示。

表3 模型一的楼层位移和层间位移角

表4 模型二的楼层位移和层间位移角

由表3可知：模型一X方向最大楼层位移为84.95 mm，Y方向最大楼层位移为106.04 mm，并且各楼层Y方向的最大楼层位移普遍比X方向大，说明模型一Y方向的抗侧刚度较小。由表4可知：增设K型偏心支撑后的模型二，X方向最大楼层位移降为58.05 mm，降幅为31.7%，Y方向最大楼层位移降为49.05 mm，降幅达到了53.7%，并且各楼层Y方向的最大楼层位移均比X方向小，说明在平面L型凹凸不规则钢框架结构中增设少量的K型偏心支撑对增强结构抗侧刚度的效果是非常显著的。

为了更好地分析增设支撑后结构的动力响应，分别绘制两种模型X方向层间位移角包络图和Y方向层间位移角包络图，如图4和图5所示。

图4反应谱分析下两种模型X方向层间位移角包络图图5反应谱分析下两种模型Y方向层间位移角包络图

由表3可知：模型一X方向和Y方向的层间位移角最大值都发生在第三层，分别为1/379和1/307，均小于1/250，符合建筑抗震设计规范中对弹性层间位移角限值的要求，但比较接近这个限值。由表4可知：模型二X方向和Y方向的层间位移角最大值都发生在第四层，分别为1/656和1/836，远小于建筑抗震设计规范中要求的1/250。由图4和图5看出，增设K型偏心支撑后，模型二中低楼层的X方向和Y方向层间位移角相比模型一降幅很大，结构抗扭刚度明显加强，确保结构安全。

2.3时程分析

时程分析方法是一种直接的动力分析方法。它通过动力方法计算得到时程波作用的各时刻各个质点的位移、速度、加速度以及各构件的内力，反映地面运动的方向、特性及持续时间的影响。在理论上，时程分析方法比反应谱法更为先进。但是由于计算量比较大以及地面运动不易预测，目前它一般作为反应谱方法的补充[8]。

本文按照建筑场地类别和设计地震分组选用两组实际强震记录和一组人工模拟的加速度时程曲线，其中实际强震记录为Elcentro波和TangShanSN波，加速度峰值分别为341.7 cm/s2和55.49 cm/s2，人工模拟的加速度时程曲线为Lanzhou波，加速度峰值为219.7 cm/s2，得到弹性时程分析下模型一和模型二的楼层位移和层间位移角，分别如表5和表6所示。

表5 弹性时程分析下模型一的楼层位移和层间位移角

续表：

表5 弹性时程分析下模型一的楼层位移和层间位移角

表6 弹性时程分析下模型二的楼层位移和层间位移角

由表5可知：模型一在Elcentro波作用下的最大楼层位移为75.43 mm，最大层间位移角为1/462；在TangShanSN波作用下的最大楼层位移为70.43 mm，最大层间位移角为1/420；在Lanzhou波作用下的最大楼层位移为14.71 mm，最大层间位移角为1/2 254；模型一在三条地震波作用下的最大层间位移角均小于1/250，符合建筑抗震设计规范中对多、高层钢结构弹性层间位移角限值的要求。

由表5、表6得到弹性时程分析下，模型一和模型二在Elcentro波、TangShanSN波、Lanzhou波下的层间位移角包络图，如图6、图7和图8所示。

图6 Elcentro波下两种模型层间位移角包络图图7 TangShanSN波下两种模型层间位移角包络图

图8 Lanzhou波下两种模型层间位移角包络图

由图6可知：在Elcentro波作用下，模型二的层间位移角相比模型一在各个楼层均有所降低，其中最大层间位移角由1/462降为1/727，降幅达36.5%。由图7可知：在TangShanSN波作用下，模型二的层间位移角相比模型一在中低楼层降幅比较明显，在高层反而有所增大，最大层间位移角由1/420降为1/546，降幅为23.1%。由图8可知：在Lanzhou波作用下，模型二的层间位移角比模型一有明显降低，但在接近顶层的位置模型二的层间位移角反而大于模型一，最大层间位移角由1/2 254降为1/3 232，降幅为30.4%。可见，K型偏心支撑对结构在三种不同地震波作用下的抗震性能均有不同程度的提升，其中对结构在Elcentro波作用下的抗震性能提升最为显著。

3 结论

本文对平面L型钢框架结构模型一和增设K型偏心支撑后的模型二进行模态分析、反应谱分析和时程分析，对抗震性能进行对比研究，得出如下结论：

(1)平面不规则结构振型比较复杂，模型一第一扭转周期出现在第二振型，模型二第一扭转周期出现在第三振型，扭转平动周期比由0.88降为0.68，可见K型偏心支撑对结构抗扭转能力提升显著。

(2)通过对模型一和模型二进行水平双向反应谱分析，可以看出结构各楼层X方向位移和Y方向位移均有大幅降低，K型偏心支撑明显提升了结构的抗侧刚度，结构更加稳定。

(3)通过对模型一和模型二的时程分析结果进行对比可知，增设K型偏心支撑后，在不同地震波作用下结构各楼层的层间位移角均有不同程度的降低，但层间位移角包络图有一定的差异，所以在实际工程中应选取尽可能多的时程曲线进行计算。

[1] 中国建设科学研究院. SATWE用户手册与技术条件[Z]. 2002.

[2] 谢立新，刘观云. 支撑对钢框架结构的性能影响[J].重庆建筑，2008(9)：16-18.

[3] 中华人民共和国住房和城乡建设部. 高层民用建筑钢结构技术规程：JGJ 99-2015[S].北京：中国建筑工业出版社，2015.

[4] 钱稼如，陈茂盛，张天申. 偏心支撑钢框架在水平力作用下的试验研究和极限分析[J].建筑结构，1993(4):3-8.

[5] 中华人民共和国住房和城乡建设部. 建筑抗震设计规范：GB 50011-2010[S].北京：中国建筑工业出版社，2010.

[6] 陈昌宏. SAP2000结构工程案例分析[M]. 北京：冶金工业出版社，2010.

[7] 北京金土木软件技术有限公司，中国建筑标准设计研究院. SAP2000中文版使用指南(第2版)[M].北京：人民交通出版社，2012.

[8] 彭俊生，罗永坤，彭地. 结构动力学、抗震计算与SAP2000应用[M].成都：西南交通大学出版社，2007.

InfluenceofK-typeeccentricsupportonseismicperformanceofsteelframestructure

WANG Song, LEI Qing-guan

(SchoolofCivilEngineering,AnhuiJianzhuUniversity,Hefei230601,China)

2017-07-01

安徽省高等学校自然科学研究重大项目(KJ2014ZD07)

王 淞(1987—)，男，河北唐山人，硕士研究生。

1674-7046(2017)04-0029-07

10.14140/j.cnki.hncjxb.2017.04.006

TU391

A