基于相位信息的图像边缘检测仿真分析

李玲香 廖承福 李艳芳



基于相位信息的图像边缘检测仿真分析

李玲香1廖承福2李艳芳1

（1.湖南科技学院 电子与信息工程学院，湖南 永州 425199；2.深圳兆日科技股份有限公司，广东 深圳 518000）

本文通过对普通图像进行傅里叶变换和反变换，证明了相位信息在图像中的重要性，并推导了基于相位一致性的边缘检测函数，最后用基于相位一致的边缘检测函数和传统的检测函数对图像进行边缘检测实验，实验结果表明了前者边缘检测效果更好，为医学超声波图像分割方法研究提供参考价值。

图像处理；相位信息；边缘检测

0 引 言

近些年来，几何活动轮廓模型在图像分割当中得到了广泛的使用，并取得了一些进展。比较经典的有GAC（Geodesic Active Contour）模型[1]和CV(Chan-Vese)模型[2]，GAC模型是一种基于边缘检测的分割模型，该模型算法有效且稳定，能够处理拓扑变化，停止项具有一定的鲁棒性。但是对于具有凹型结构的物体，或者带有噪声，边缘比较模糊的图像，分割效果不是很好。CV模型的显著优点是基于全局的优化，该模型对图像边缘信息的依赖较弱，初始轮廓曲线可以在任意位置，不须设置在目标边缘的周围。而且对于有空洞的目标，CV模型也能将其检测出来。由于CV模型运用了水平集的原理，为了使水平集保持为信号距离函数(Signed Distance Function，SDF)在每次迭代后都得重新初始化水平集函数，否则，将会发生数值错误，造成分割效果不理想，同时重新初始化水平集函数是一件较为麻烦的工作。

1 基于传统的边缘检测函数

基于边缘检测的活动轮廓模型主要利用图像的边缘信息作为模型中的停止准则。当曲线到达目标边缘时，停止演化。所以基于边缘检测的几何活动轮廓模型对图像分割的效果，取决于边缘检测函数[3]的定义。

(z)是一个递减函数，满足如下性质：

(2)

2 基于相位信息的边缘检测函数

2.1相位信息重要性的证明

为了证明图像中相位信息的重要性，本文用两幅图像来做实验，如图1所示。分别对图1中的（a）和（b）两幅图像原图做傅里叶变换，得到它们的相位信息和幅度信息，图1中(c)和（d）是 (a)原图的相位信息和幅度信息。图1中(e)和(f)的分别是 (b)原图的相位信息和幅度信息。若将两幅图像的幅度信息和相位信息分别交换，然后再进行傅里叶逆变换，得到图像（g）和（h）。从结果图1(g)和图1(h)可以看出，图像的幅度信息基本上被隐藏了，只能通过相位信息看到原图像，该实验充分证明了相位信息比幅度信息更能体现图像的特征，因此在图像中，相位信息比幅度信息更重要。

(d)图(a)的幅度信息(e)图(b)的相位信息(f)图(b)的幅度信息

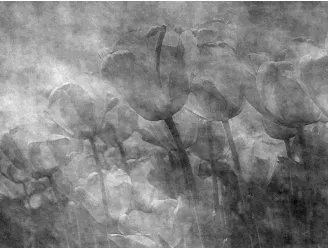
(g)图(a)的幅度加图(b)的相位（h)图(a)的相位加图(b)的幅度

图1.相位信息重要性的验证

2.2 Log-Gabor滤波器

Gabor小波被应用于各种图像特征提取场合[4-5]，但是，利用Gabor 小波直接进行频域或空间域滤波，并不是最理想的选择。Gabor滤波器存在的主要问题是：一是带宽有限，其最大的带宽只限制在一倍频；二是Gabor滤波器往往过度表示信号的低频分量，而对高频分量往往表示不足。

Field提出的Log-Gabor函数解决了上述问题，该函数即可以构建任意带宽的Log-Gabor滤波器，还能很好的保护信号的相位信息。Log-Gabor滤波器频率域的转移函数表达式为：

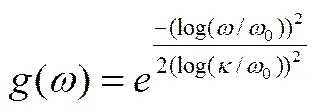
Log-Gabor 函数具有两个重要特征[6]：首先，Log-Gabor 函数总是没有直流分量；其次，Log-Gabor函数的传递函数在高频端存在较长的拖尾，如图2所示。

Field等人关于图像统计的研究表明，自然图像的幅度大概在附近开始减弱，要对具有这种频谱特征的图像进行编码，就必须使用具有相似频谱特征的滤波器。根据文献[6-7]，Log Gabor 函数在对数频率空间呈现为高斯函数，因此，在对数频率尺度上传递函数为高斯函数的滤波器可以对图像进行更有效的编码。由于Gabor函数的传递函数只有在线性频率尺度上为高斯函数，所以Log-Gabor 函数更能够真实地反映自然图像的频率响应。

图2.Log-Gabor的幅频图（=0.3，=0.41）

2.3基于相位一致性的边缘函数

估计信号局部信息的常用方法是将信号表示成解析信号的形式。由于用生成一维解析信号的方法生成的相位无法对二维信号的结构进行编码，因为它没有足够大的自由度。那么对于二维或者二维以上的信号，该如何生成解析信号呢？针对上述情况，Felsberg和Sommer提出了一种理想的二维解析信号的生成方法[8-9]，利用Riesz变换代替希尔伯特变换，生成二维解析信号，也称之为单演信号。单演信号保留一维解析信号的一些重要特性，比如将一个信号分解成结构信息（局部相位）和能量（局部幅度）信息。

在实际应用中，信号的局部特征可以通过一组带通滤波器来实现。因为一幅图像中的频率成分不是帯限的，所以必须使用Log-Gabor带通滤波器对它的单演信号进行滤波。单演信号通过Log-Gabor滤波器滤波之后的表达式为：

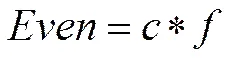
(6)

Peter Kovesi提出，在非对称点处，奇对称滤波器的输出远远大于偶对称滤波器的输出；而在对称点处则相反，即偶对称滤波器的输出远远大于奇对称滤波器的输出。为了检测阶跃边缘，Peter Kovesi提出了一种利用非对称特征进行阶跃边缘检测的相位一致性函数[10]，其表达式为：

图3.FA边缘检测示意图

实验结果表明：随着滤波器尺度的增大，检测函数对图像细节部分的检测逐渐变弱，主要目标的轮廓边缘逐渐清晰。但的取值也不能太大，否则边缘检测效果变得不理想。如图3(e)，为12的时候，检测出来的边缘开始变得模糊。所以，应该根据具体情况来选取的值，从而使边缘检测的效果达到最佳。

3 实验仿真分析

为了进一步说明基于相位信息一致性的边缘检测函数的优点，本文从多个角度，将传统的基于梯度信息的边缘检测函数的检测效果与之进行比较。

3.1 对于普通图像边缘检测

图4(a)为普通图像边缘检测实验的原图，图4 (b)为加入斑点噪声之后的图像，噪声方差为0.05。图4 (c)为对原图检测的边缘效果图，(d)为FA对原图的边缘检测效果图，从结果可以看出两者的检测效果近似。图4 (e)，图4 (f)分别为和对带噪声图像的检测效果图，实验结果表明：对带有噪声的图像边缘检测效果较差，检测出的边缘相比于其他区域不够明显。而几乎不受噪声的影响，依然能够检测出明显的边缘。

图4.普通图像的边缘检测对比图

3.2 对超声波图像的边缘检测

图5(a)是一幅超声图像，图中黑色区域为病灶，现分别用g和FA对其进行边缘检测，检测的效果见图5(b)和图5(c)。同样的，g对带有噪声的图像检测效果不太理想。

图5.超声图像边缘检测对比图

3.3 对低对比度图像的边缘检测

图6(a)是一幅对比度较低的图像，即目标的边缘与周围比较不明显。图6(b)和图6(c)分别为g和FA的检测效果图。从实验检测结果来看，FA对低对比度图像的边缘检测能够达到令人满意的效果。

图6.低对比度图像边缘检测对比图

4　结束语

本文在单演信号的形成过程Log-Gabor滤波器的原理的基础上，推导了基于相位一致性的边缘检测函数，并用基于相位一致的边缘检测函数和基于梯度信息的边缘检测函数分别对图像做边缘检测实验，通过对比实验可知，对不带噪声的普通图像进行边缘检测，两者的检测效果相当。但是，若图像中加入噪声后，传统的边缘检测函数的检测效果并不理想，表明基于梯度的检测方法对噪声很敏感；而基于相位一致性的检测函数的检测效果仍然比较理想，表明了基于相位信息的检测方法对噪声的抑制能力较强。同样地，对带有噪声的超声图像进行实验，也表明了基于相位一致性检测方法的优越性。最后，对一幅低对比度图像进行检测，实验结果表明基于相位信息的检测方法对低对比度的，或者边缘比较模糊的图像的检测效果依然较好。因此，基于相位一致的边缘检测函数图像分割方法对于临床超声肿瘤图像病灶提取方法的研究提供参考价值。

[1]V.Caselles,R.Kimmel,and G. Sapiro,Geodesic ActiveContours,Proc.IEEE Int’l Conf.Computer Vision,pp.694-699,1995.

[2]T.Chan and L.Vese,An Active Contour Model without Edges, Proc.Int’l Conf.Scale-Space Theories in Computer Vision, pp.141-151,1999.

[3]V.Caselles,F.Catte,T.Coll,and F.Dibos,A geometric model for active contours,Number.Math.,vol.66,no.1,pp.1–31,1993.

[4]Yang X,Zhang X.Gabor filter bank and its application in the fingerprint texture analysis[C]//Proceedings of the 6th Inter- national Conference on Parallel and Distributed Computing, Applications and Technologies(PDCAT05).The IEEE Com- puter Society,pp:829-831,2005.

[5]Lin H,Wan Y F.Jain A.Fingerprint image enhancement: algorithm and performance evaluation[J].Pattern Analysis and Machine Intel-ligence,1998,(8):777-788.

[6]D.J.Field. Relations between the statistics of natural images and the response properties of cortical cells[J].Journal of the Optical Society of America A,1987,(12):2379-2394.

[7]Kovesi P.Image features from phase congruency[J].Videre: Journal of Computer Vision Research,1999,(3):1-27.

[8]M.Felsberg and G. Sommer,The monogenic signal,IEEE Trans.Signal Process.,vol.49,no.12,pp.3136-3144,Dec.2001.

[9]T.Bülow,D.Pallek,and G.Sommer,Riesz transforms for the isotropic estimation of the local phase of moire interfero grams,in 22nd DAGM Symp.Mustere rkennung,G.Sommer, Ed.,Heidelberg,Germany,pp333-340,2000.

[10]Peter Kovesi,Symmetry and Asymmetry From Local Phase,Tenth Australian Joint Conference on Artificial Intelligence.Proceedings-Poster Papers.pp185-190.1997.

（责任编校：宫彦军）

2017－04－05

永州市科技局项目(永科发[2015]号40015)；湖南科技学院电路与系统重点学科资助项目。

李玲香（1976－），女，湖南郴州人，湖南科技学院讲师，研究方向为无线通信、信号与信息处理。

TP183；TB115；O24

A

1673-2219（2017）06-0017-04