基于能量守恒原理的金属压缩流动应力修正方法

贾 东，黄西成，莫 军，胡文军



基于能量守恒原理的金属压缩流动应力修正方法

贾 东，黄西成，莫 军，胡文军

(中国工程物理研究院总体工程研究所，绵阳 621900)

通过轴对称缺口圆柱试件设计，消除了端面摩擦对金属(特别是延性金属)试件压缩变形行为的影响。基于压缩过程中外力功与试件内能之间的能量守恒原理，推导了压缩流动应力的近似修正公式，并给出了相应的迭代修正过程。针对铝合金2024，利用修正后的流动应力−应变关系对压缩过程中试件的最小横截面直径和内能进行了预测，并与实验结果进行了比较。研究结果表明：在整个压缩过程中，试件的最小横截面直径的预测值与实验值吻合，且试件内能与实验外力功始终保持一致，从而验证了该修正方法的有效性。

流动应力；端面摩擦；缺口圆柱试件；能量守恒；迭代修正

有限元数值模拟是金属塑性成形过程分析的重要研究手段，而准确的流动应力−应变关系是对该过程进行数值分析的重要前提。由于金属成形过程主要处于压应力状态，且压缩实验可以获取更大塑性变形量的应力−应变曲线，所以如何获取准确的压缩流动应力−应变曲线是非常重要的。

目前，金属材料压缩应力−应变关系主要通过轴对称圆柱试件压缩实验获取，但由于压头与试件端面之间的摩擦约束，试件在整个压缩过程中无法保持均匀应力状态，这对金属材料(特别是延性金属)压缩流动应力−应变曲线的准确性影响很大[1]。消除或修正这种端面摩擦约束影响的方法主要有以下几种：一是通过在接触面上添加润滑剂或在试件端面设计凹槽等方式来直接减小摩擦作用[2]，这种方法对于大变形的延性金属效果并不理想，当压缩载荷逐渐增大时，两接触面间的润滑作用会逐渐减弱，凹槽面会产生明显的塑性变形，从而影响对摩擦的消除效果[3]；二是COOK等[4]提出的外推法，通过多组不同长径比的圆柱试件压缩实验找到应力随长径比变化的规律，再外推得到长径比无穷大(无摩擦状态)时的应力，该方法避免了对压缩端面真实摩擦约束情况的分析，但其外推结果精度受限于试件的长径比范围，当长径比较大时试件易发生屈曲，从而导致实验无效；三是利用试件变形特征求解端面摩擦因数，进而对流动应力进行修正，这其中以圆柱试件鼓度法[5−10]以及圆环镦粗法[11−15]最为典型，在这些方法中，端面摩擦行为常常被假设为特定的线性摩擦模型，并以平均摩擦因数表征整个接触面的摩擦特性。但在压缩过程中，随着载荷的增大，试件端面的不同区域常常处于不同的摩擦类型，且不同类型之间还会发生相互转换，摩擦常表现出非线 性[16]，所以端面摩擦行为描述的准确性将会直接影响到流动应力的修正计算。除此以外，目前最为常用的是实验和数值模拟相结合的各种逆向求解方法[17−19]，但这些方法需要给出应力、几何参数以及摩擦因数等之间准确的数学函数关系。总的来说，上述各种实验及有限元方法对端面摩擦约束的修正都有其自身的缺点或局限性，这是由于端面摩擦行为的复杂性所造成的。

本文作者为了避免对试件端面复杂摩擦行为的分析，采用新型的缺口圆柱试件设计来消除端面摩擦约束对试件压缩变形的影响。基于缺口试件压缩过程中的能量守恒原理推导压缩流动应力的近似修正公式，同时结合有限元分析，对流动应力进行迭代修正，获取金属材料准确的压缩流动应力−应变关系。

1 流动应力修正方法

1.1 近似修正公式

在端面摩擦等约束存在时，压缩外力所做的功F将转化为两部分能量：一部分转化为试件的塑性应变能P储存在试件中；另一部分则转化为试件端面与压头之间的摩擦功f。所以外力功可以表示为

式中：为压缩过程中试件所受的外力，为试件的位移。而塑性变形能和压缩过程中摩擦作用所耗散的能量可以分别表示为

(2)

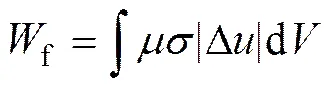
式中：0为试件的应变能密度，是试件的体积，为试件端面的摩擦因数，Δ为试件端面的滑移速度。为了避免对端面复杂的摩擦行为进行描述，这里采用缺口圆柱试件设计来消除端面摩擦的影响[20]，如图1所示。在压缩过程中，试件端部不会发生变形，压头和试件端面之间没有相对滑动，从而也没有磨擦作用所带来的能量耗散。

图1 缺口圆柱试件压缩

Fig. 1 Compression of notched cylindrical specimen

所以，通过这样的试件设计就可以使试件在压缩过程中外力所做的功将完全转化为试件的塑性应变能：

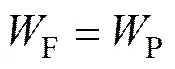
由于外力功完全转化为试件的变形能，所以这里将缺口试件模型近似等效为一个无端面摩擦作用的理想圆柱试件压缩模型。对于理想圆柱压缩模型，试件在压缩过程中应力、应变状态均匀，所以塑性变形能P可以表示为

(5)

在压缩过程中，试件在任一时刻的轴向位移()和真实应变()可以表示为

(7)

(8)

式中：U为=1时的轴向位移，为一无量纲时间参数，0≤≤1；0为理想圆柱试件的初始高度；为=1时的真实应变。所以，在U/0较小时，忽略二阶及其以上的高阶项，等式(8)可以表示为

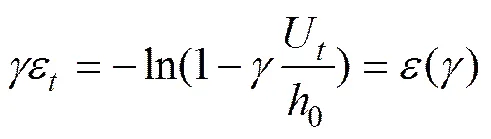
将式(6)和式(9)分别代入式(2)和(5)中，可以得到外力功和塑性变性能以及Δ的表达式为

(10)

(12)

由于在压缩过程中能量守恒，所以对于任一时刻，上述等式均成立，所以在时刻，即=1时，由上述方程可以得到

假设此时等效圆柱试件的轴向压缩位移为，高度为，真实应变为，真实压缩流动应力为1，待修正的压缩流动应力为2，于是可以得到

(14)

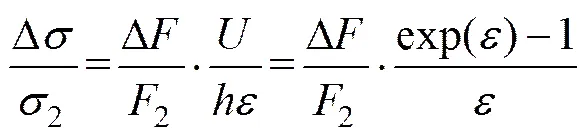
(16)

式中：1为缺口试件压缩实验的真实载荷，2为以流动应力2作为输入进行缺口试件压缩实验模拟得到的载荷。可以看出，在小应变范围内，上述修正关系能较好地成立；而当试件塑性变形较大时，公式(8)中忽略的高阶项所引进的误差将会影响流动应力的修正结果。所以对于塑性变形较大的延性金属材料而言，单次修正的效果是不够理想的。

1.2 迭代修正步骤

为了减小近似修正公式在大变形条件下产生的误差，得到更加准确的材料应力−应变曲线，这里需要结合有限元分析对流动应力进行迭代修正。在迭代修正过程中，和的值会逐渐减小，流动应力−应变曲线也会逐渐收敛。基于上述分析，这里给出有限元迭代修正方法的具体修正过程：

1) 通过光滑圆柱试件压缩实验获取材料的初始流动应力−应变曲线；

2) 利用设计的缺口试件进行压缩实验获取其真实的载荷−位移曲线；

3) 将获取的流动应力−应变曲线作为本构输入对缺口试件压缩过程进行有限元模拟，获取材料的载 荷−位移曲线；

4) 将步骤(3)得到的载荷−位移曲线与缺口试件压缩实验得到的载荷−位移曲线进行比较，如果载荷的相对误差值大于规定值，则利用公式(16)对真实流动应力值进行计算，得到修正后的流动应力−应变曲线；

5) 重复步骤3)和4)，直至载荷的相对误差值收敛到规定的误差值范围内。

2 铝合金2024轴对称圆柱试件压缩

2.1 圆柱试件压缩实验

本实验中所用材料为铝合金2024，其主要力学性能参数如下：弹性模量71 GPa，泊松比0.3，密度2.78 g/cm3；所用试件为两种轴对称圆柱试件，分别为12 mm×12 mm的光滑圆柱试件以及整体尺寸为16 mm×24 mm的缺口圆柱试件。在常温、准静态条件下对两种试件进行单轴压缩加载，并记录整个加载过程的载荷−位移曲线以及试件的变形过程。

在光滑圆柱试件压缩实验中，试件会发生整体变形，当压头与试件端面之间存在摩擦作用时，试件的变形会变得不均匀，在试件中部会出现鼓胀效应；而对于缺口圆柱，无论端面摩擦是否存在，其全部变形都集中在试件的中部区域，试件的端部不会发生变形，如图2所示。

图2 不同类型圆柱试件的压缩

从图2还可以看出，无论是光滑圆柱试件还是缺口圆柱试件，其最终的破坏形式均为沿45°方向的剪切破坏，并且裂纹均是从试件中部表面开始产生，这是由于试件端部约束(光滑圆柱试件主要为端面摩擦，缺口圆柱试件可以视为端部固约束)作用下，试件中部的鼓胀区域表面会出现拉应力，从而导致此处的剪切应力增大，最终使试件从这里开始发生破坏。而由于缺口试件的特殊构型，在压缩加载初期，试件缺口部位处于多向压缩应力状态，所以其压缩过程中的鼓胀效应要明显弱于光滑圆柱试件，试件中部的拉应力也相对更小，从而“减缓”了试件的破坏，可以使试件获得更大范围的塑性应变，这也说明利用缺口圆柱试件压缩实验对流动应力−应变曲线进行修正是可行的。

通过压缩实验得到的光滑圆柱试件的真实应力−应变曲线和缺口圆柱试件的载荷−位移曲线分别如图3和图4所示。

2.2 缺口试件压缩过程数值模拟

本研究利用ABAQUS/Standard对缺口试件的压缩过程进行数值模拟分析，鉴于缺口试件的几何特征，这里采用轴对称模型，如图5所示。试件网格单元类型采用4节点轴对称单元，两端压头采用刚性单元，压头与试件端面之间接触类型为面面接触。在压缩过程中，模型下端轴向位移固定不变，上端以恒定速度进行压缩加载，数值模拟加载位移与真实实验位移保持一致。

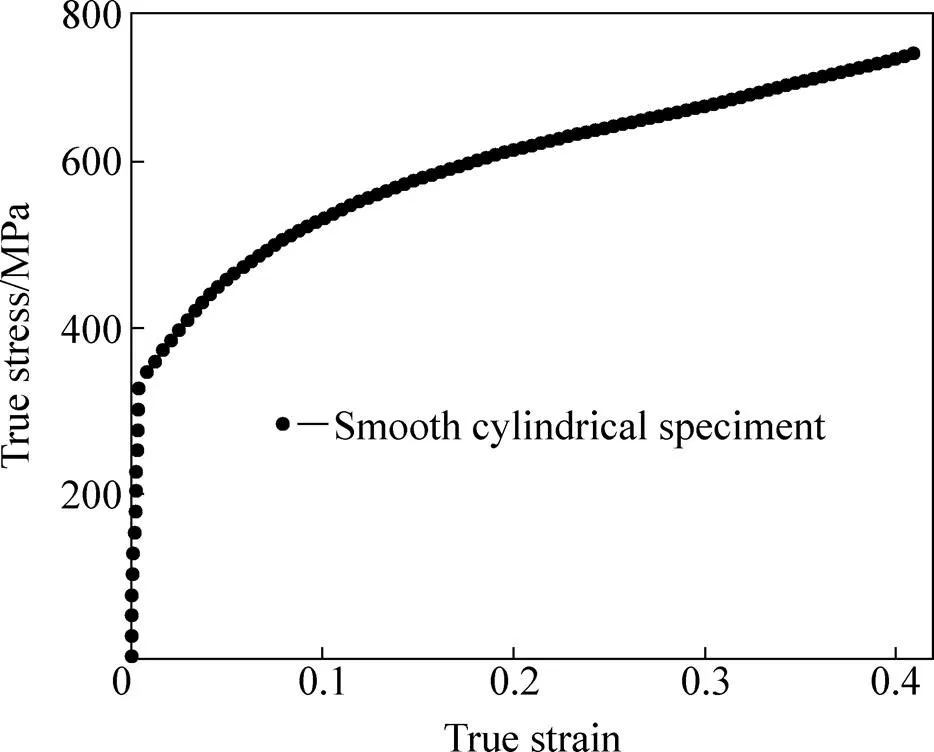
图3 光滑圆柱试件的真实应力−应变曲线

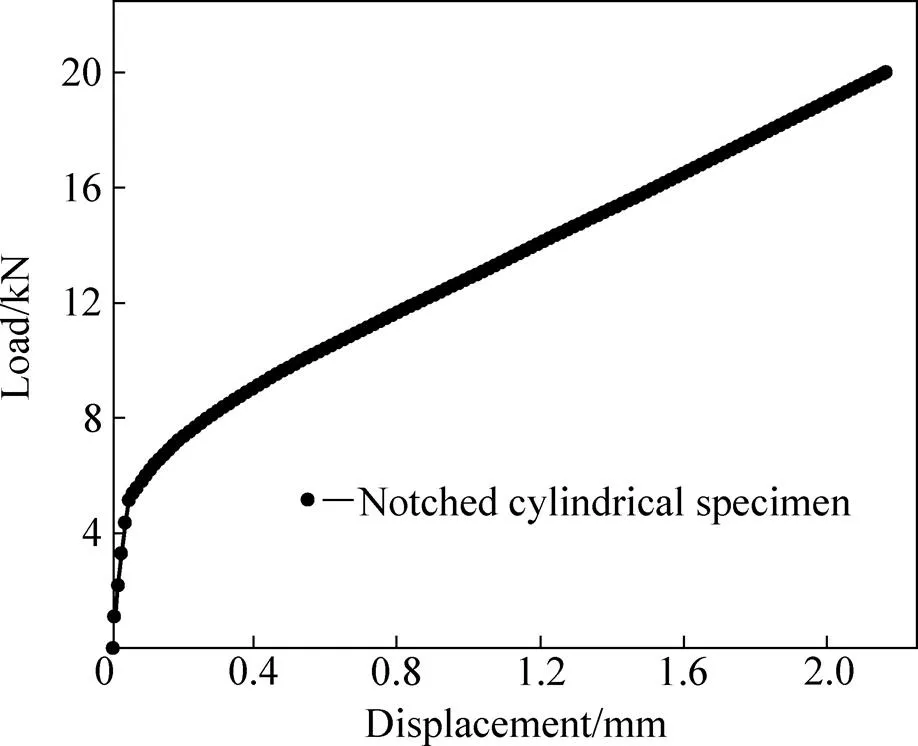
图4 缺口圆柱试件的载荷−位移曲线

为保证有限元模型单元尺寸不对修正结果造成影响，这里以4种不同的单元尺寸(1.6 mm、0.8 mm、0.4 mm以及0.2 mm)对试件模型进行网格划分，并以不同单元尺寸下的载荷−位移关系响应对网格密度敏感性进行了分析，如图6所示。

从比较结果可以看出，试件有限元模型对网格密度存在一定的敏感性，当单元尺寸逐渐减小时，试件的载荷−位移曲线逐渐收敛，直至单元尺寸减小到0.4 mm以内时，载荷−位移曲线基本趋于一致。所以，为了避免网格密度对修正结果的影响，这里取0.2 mm为试件有限元模型的单元尺寸。

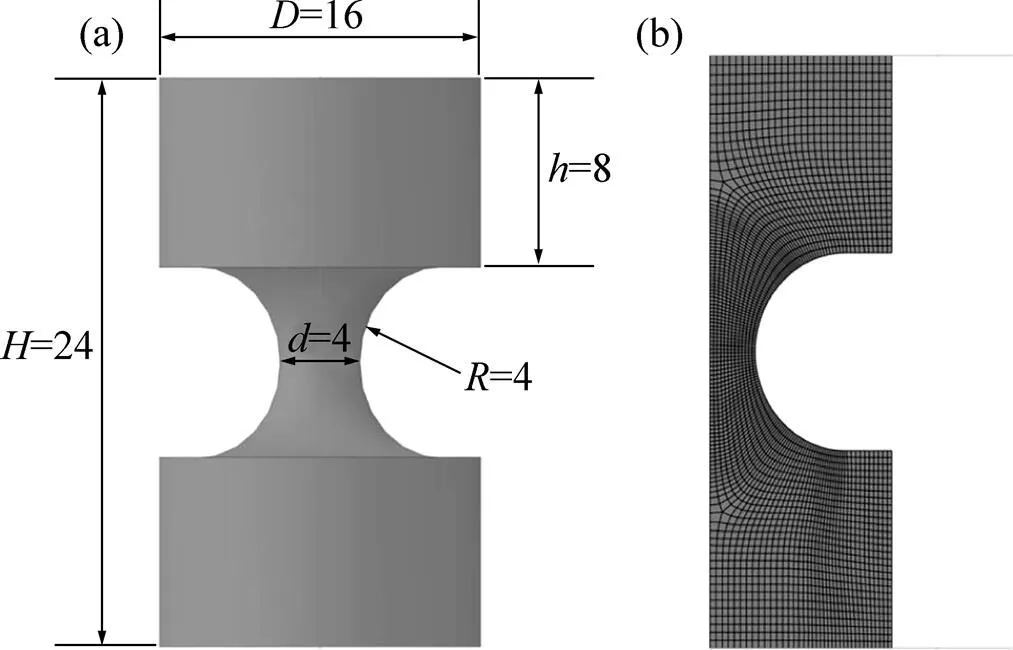
图5 缺口试件模型

图6 缺口圆柱试件在不同单元尺寸下的载荷−位移曲线

3 结果与讨论

3.1 端面摩擦对缺口试件压缩变形行为的影响

为了进一步研究端面摩擦对缺口试件压缩过程的影响，这里利用光滑圆柱试件压缩实验得到的流动应力本构关系对不同摩擦情况(无摩擦、=0.2、=0.4、=0.8以及粗糙表面)下缺口试件压缩变形进行数值模拟，得到了试件轴向压缩载荷随位移的变化，如图7所示。

从图7可以看出，不同摩擦情况下，试件在相同压缩位移量下所受的载荷是相同的。所以对于同一材料和几何尺寸的缺口试件来说，摩擦约束存在与不存在时试件的载荷−位移曲线都是相同的，进而说明压缩载荷所做的功也是一样的。

数值模拟结果表明，不同摩擦条件下试件端部几乎没有变形，所有变形均集中在试件中部。以无摩擦和粗糙表面情况下的变形结果进行比较知道，在相同压缩位移下，试件径向位移和等效塑性应变分布一致，都分布在试件缺口区域，且最大偏差均不超过0.5%，如图8所示，这与缺口试件压缩实验现象也是吻合的。所以，对于缺口试件，压头与试件端面之间摩擦力的影响可以忽略不计。

图7 缺口圆柱试件在不同端面摩擦条件下的载荷−位移曲线

3.2 流动应力迭代修正

按照修正方法中的迭代修正步骤对初始流动应力进行修正，得到了不同迭代次数下的铝合金2024的流动应力−塑性应变曲线以及对应载荷−位移曲线分别如图9和10所示。

从图9和10中可以看出，在迭代修正过程中，铝合金2024的流动应力逐渐趋于一致，且经过4次的迭代修正后，其流动应力基本保持稳定，对应的载荷−位移曲线与实验结果吻合很好。在修正过程中，载荷相对误差的绝对值随着迭代次数的增加而不断减小，如图11所示。

从图11比较结果可以看出，利用修正公式进行单次修正后，相对载荷误差值依旧较大，且随着应变的增加误差逐渐增大，但经过4次迭代修正后，载荷的最大相对误差值已从初始状态的11%减小到1%左右，这说明迭代过程是收敛的。为了更进一步验证修正结果的准确性，这里利用光滑圆柱试件压缩实验得到的流动应力本构关系以及经过4次迭代修正后的流动应力本构关系对缺口试件压缩过程中缺口根部横截面的直径变化进行模拟预测，并与不同载荷水平下的实验测量结果进行比较，其结果如图12所示。

图8 缺口圆柱试件的压缩变形数值模拟

从图12对比结果可以看出，经过迭代修正后的流动应力本构关系能非常好地模拟出缺口试件压缩实验过程中试件根部横截面直径的变化情况，而未经修正的本构关系预测结果则随着压缩载荷的增加偏差越来越大。同时，从功能转化的角度来说，本修正方法成立的前提是外力功与试件内能之间的能量守恒，所以这里采用公式(1)对缺口试件压缩实验获取的载荷−位移曲线进行积分计算实验过程中的外力功，然后在相同压缩位移下分别采用初始流动应力本构以及经过4次迭代修正后的流动应力本构对缺口试件压缩过程进行模拟，得到两种本构输入下试件的内能，并将其与真实实验过程的外力功进行比较，其结果如图13所示。

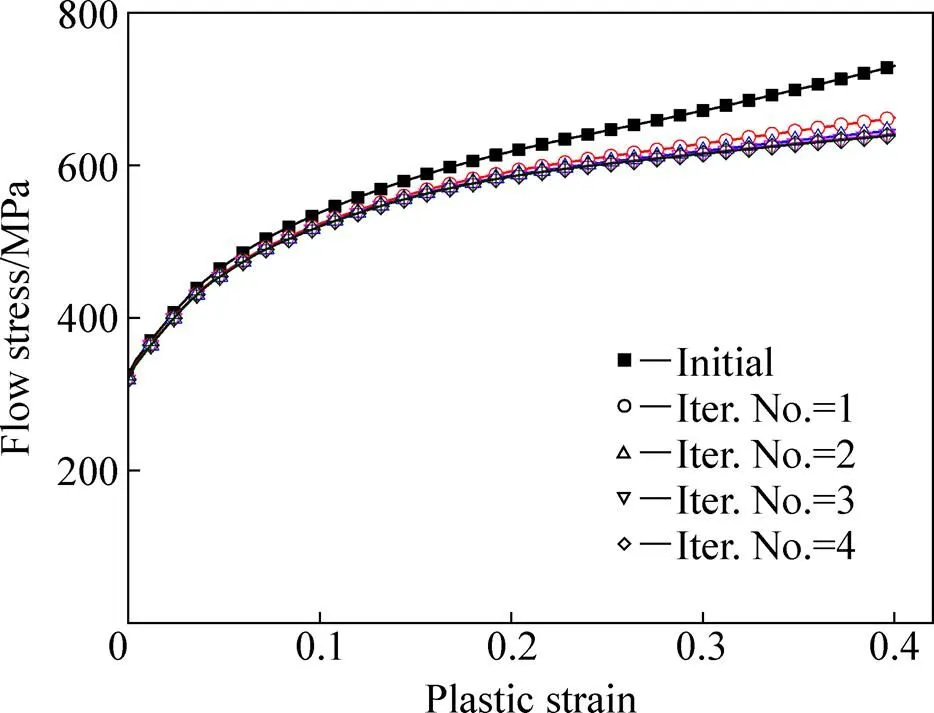
图9 不同迭代次数下的流动应力−塑性应变曲线

图10 载荷−位移曲线模拟结果与实验结果的比较

图11 不同迭代次数下的相对载荷误差值

从图13可以看出，在不同压缩位移量下，经过迭代修正后的流动应力本构关系模拟得到的试件内能与实验载荷−位移曲线计算得到的外力功始终保持一致，这也从能量守恒的角度证明了迭代修正结果的准确性。

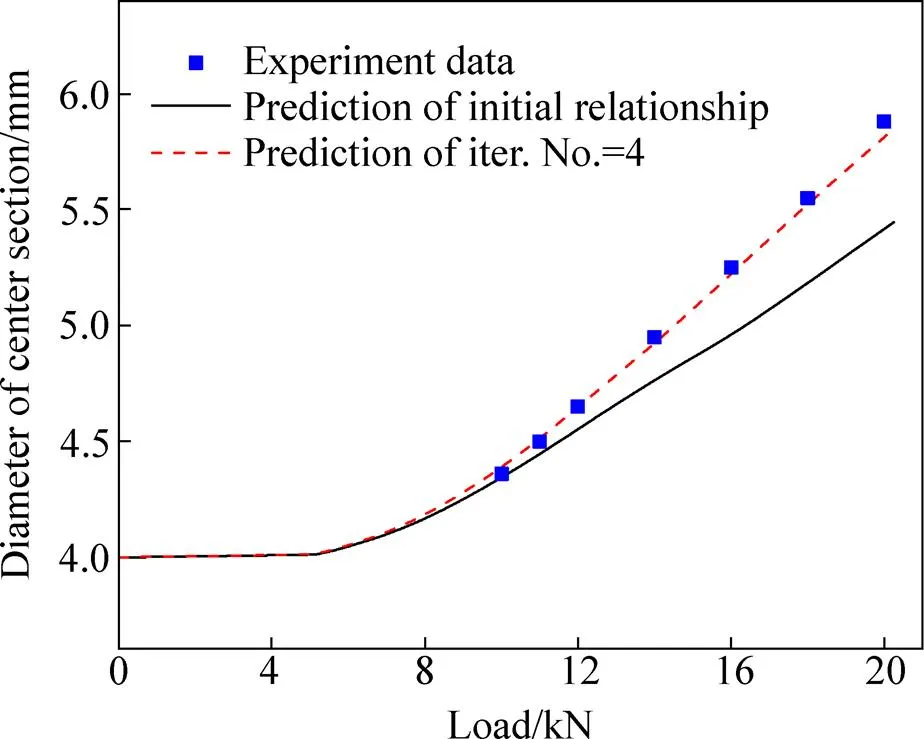
图12 缺口圆柱试件根部横截面直径模拟预测与实验结果的比较

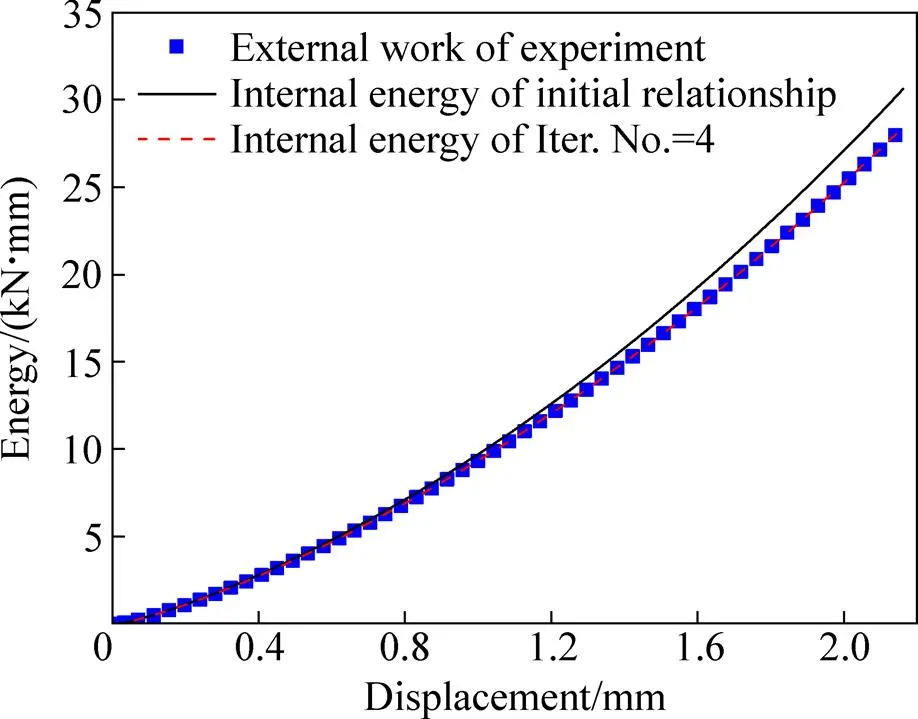
图13 缺口圆柱试件内能与实验外力功的比较

4 结论

1) 缺口圆柱试件的设计有效地避免了对压缩实验中压头与试件端面之间复杂摩擦行为的分析，基于此设计提出了以能量守恒原则为基础的流动应力近似修正公式。

2) 借助于有限元数值模拟分析，结合流动应力近似修正公式可以对金属材料压缩流动应力进行迭代修正，得到收敛后的流动应力值。

3) 以铝合金2024为例，对该修正方法进行了验证，其结果证明经该修正方法得到的流动应力−应变关系可以很好地预测铝合金2024在压缩过程中的变形行为，并使试件内能与实验得到的外力功在整个压缩过程中保持一致。

REFERENCES

[1] EVANS R W, SCHARNING P J. Strain inhomogeneity in hot axisymmetric compression test[J]. Materials Science and Technology, 2002, 18(11): 1389−1398.

[2] JOHNSON W. Experiments in plane-strain extrusion[J]. Journal of the Mechanics and Physics of Solids, 1956, 4(4): 269−282.

[3] BAO Y B. Prediction of ductile crack formation in uncracked bodies[D]. Cambridge: Massachusetts Institute of Technology, 2003.

[4] COOK M, LARKE E C. Resistance of Copper and Copper Alloys to Homogeneous Deformation in Compression[J]. Journal of the Institute of Metals, 1945, 71(12): 371−390.

[5] EBRAHIMI R, NAJAFIZADEH A. A new method for evaluation of friction in bulk metal forming[J]. Journal of Materials Processing Technology, 2004, 152(20): 136−143.

[6] LIN J F, FENG L I, ZHANG J F. A new approach to investigate real flow stress in micro-extrusion[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S2): s232−s238.

[7] YAO Z H, MEI D Q, SHEN H, CHEN Z C. A friction evaluation method based on barrel compression test[J]. Tribology Letters, 2013, 51(3): 525−535.

[8] 段园培, 黄仲佳, 余小鲁, 邢 昌, 孙宇峰. 基于摩擦修正的TB6合金流变应力行为研究及本构模型建立[J]. 稀有金属, 2014, 38(2): 202−209. DUAN Yuan-pei, HUANG Zhong-jia, YU Xiao-lu, XIN Chang, SUN Yu-feng. Flow stress behavior and constitutive model of As-Cast TB6 titanium alloy based on friction correction. Chinese Journal of Rare Metals, 2014, 38(2): 202−209.

[9] 陈 前, 王 岩.相时效态GH4169合金的热加工行为[J]. 中国有色金属学报, 2015, 25(10): 2727−2737. CHEN Qian, WANG Yan. Hot working behavior of delta-processed GH4169 alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2727−2737.

[10] 司家勇, 廖晓航, 黄再旺, 江 亮. DP工艺inconel718合金高温流变曲线修正及应变本构模型[J]. 中国有色金属学报, 2015, 25(12): 3361−3369. SI Jia-yong, LIAO Xiao-hang, HUANG Zai-wang, JIANG Liang. Revised hot derofmation behavior and strain constitutive modeling of delta-processed Inconel718 alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(12): 3361−3369.

[11] WANG J P, LIN F L, HUANG B C, YUN C C. A new experimental approach to evaluate friction in ring test[J]. Journal of Materials Processing Technology, 2008, 197(1): 68−76.

[12] 邰清安, 李晓光, 李治华, 刘 艳, 朱艳春, 曾卫东. 应用FEM与圆环镦粗实验测定TC4钛合金高温变形时的摩擦因数[J]. 材料工程, 2011(6): 23−26, 31. TAI Qing-an，LI Xiao-guang，LI Zhi-hua，LIU Yan，ZHU Yan-chun，ZENG Wei-dong. On the measurement of friction coefficient of Ti-6Al-4V titanium alloy utilizing the hot compression test of ring and FE simulation[J]. Journal of Materials Engineering, 2011(6): 23−26, 31.

[13] 陶 欢, 曾卫东, 朱艳春, 邰清安, 李晓光, 李治华. 热传导系数对TC4钛合金热变形过程摩擦因数测定的影响[J]. 中国有色金属学报, 2012, 22(10): 2762−2767. TAO Huan, ZENG Wei-dong, ZHU Yan-chun, TAI Qing-an, LI Xiao-guang, LI Zhi-hua. Effect of heat transfer coefficient on measurement of friction factor in hot deformation of Ti-6Al-4V alloy[J]. The Chinese Journal of Nonferrous Metals, 2012, 22 (10): 2762−2767.

[14] FERESHTEH-SANIEE F, NOURBAKHSH S H, PEZESHKI S M. Estimation of flow curve and friction coefficient by means of a one-step ring test using a neural network coupled with FE simulations[J]. Journal of Mechanical Science and Technology, 2012, 26(1): 153−160.

[15] DESALEGN W, DAVIDSON M J, KHANRA A K. Friction factor evaluation using experimental and finite element methods for Al-4%Cu Preforms[J]. Journal of Materials Engineering and Performance, 2014, 23(8): 3058−3068.

[16] BARRAU O, BOHER C, GRAS R, REZAI-ARIA F. Analysis of the friction and wear behavior of hot work tool steel for forging[J]. Wear, 2003, 255(7): 1444−1454.

[17] HAN H. Determination of mean flow stress and friction coefficient by the modified two-specimen method in cold rolling[J]. Journal of Materials Processing Technology, 2005, 159(3): 401−408.

[18] SHIN K, CHI S, KIM N. Prediction of flow stress of metallic material and interfacial friction condition at high temperature using inverse analysis[J]. Journal of Mechanical Science and Technology, 2010, 24(3): 639−648.

[19] CHRISTIANSEN P, MARTINS P A F, BAY N. Friction compensation in the upsetting of cylindrical test specimens[J]. Experimental Mechanics, 2016, 56(7): 1271−1279.

[20] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81−98.

(编辑 何学锋)

Correction method of compression flow stress of metals based on energy conservation principle

JIA Dong, HUANG Xi-cheng, MO Jun, HU Wen-jun

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

The influence of interfacial friction on the compressive deformation behavior of metals (especially ductile metals) was eliminated by design of axisymmetric notched cylindrical specimen. Based on the energy conservation between external work and internal energy of specimen in compression test, an approximate correction formula of compression flow stress was derived and the corresponding iterative correction procedure was proposed. For aluminum alloy 2024, both the diameter of minimum cross-section and the internal energy of specimen in compression process were predicted by the corrected flow stress-strain relationships and compared with the experimental results. The results show that the predicted diameters of minimum cross-section are agree with the experimental data and the internal energy of specimen is always consistent with the experimental external work in the whole compression process, which verify the effectiveness of the correction method.

flow stress; interfacial friction; notched cylindrical specimen; energy conservation; iterative correction

Project(11472257) supported by the National Natural Science Foundation of China; Project(13CXJ09) supported by Innovation and Development Foundation of Institute of Systems Engineering, China Academy of Engineering Physics

2016-05-26; Accepted date: 2016-11-02

JIA Dong; Tel: +86-816-2484030; E-mail: jiadong@mail.ustc.edu.cn

10.19476/j.ysxb.1004.0609.2017.07.15

1004-0609(2017)-07-1433-08

TG115

A

国家自然科学基金资助项目(11472257)；中国工程物理研究院总体工程研究所创新与发展基金资助项目(13CXJ09)

2016-05-26；

2016-11-02

贾 东，助理研究员；电话：0816-2484030；E-mail：jiadong@mail.ustc.edu.cn