中国牛市真的是“水牛”吗？——不确定性视角下股市价量关系的实证研究

石建勋,王盼盼,何宗武

(1.同济大学经济与管理学院，上海 200092；2.同济大学财经研究所，上海 200092；3.台湾世新大学财务金融学系，台湾 台北 11645)

中国牛市真的是“水牛”吗？
——不确定性视角下股市价量关系的实证研究

石建勋1,2,王盼盼1,2,何宗武3

(1.同济大学经济与管理学院，上海 200092；2.同济大学财经研究所，上海 200092；3.台湾世新大学财务金融学系，台湾 台北 11645)

由于我国股市时常发生大幅波动，结构变动和市场波动性因素可能会对价量关系产生重要影响。因为价量同期内生性问题，以往的实证研究通常在VAR框架下进行，但利用传统线性VAR方法无法识别价量动态关系的非对称性变动特征。为此，本文通过采用门限VAR模型，在价量关系的VAR框架中嵌入结构变化和市场波动的门限变量，研究发现：第一，在2007-2008和2014-2015年股市大幅波动期间价量关系存在显著的时间断点效应，且后者结构变化更剧烈；第二，市场不确定性(波动率)显著影响价量关系，随着波动率增加，交易量对价格影响逐渐消失，而价格对交易量的影响始终高度显著，但经济显著性也逐渐下降；最后，中国股市中价格显著引导交易量的变动，是价格拉动型而非资金推动型市场，因此“水牛”的说法并不准确。

股市价量动力学；结构变动；市场不确定性；门限VAR模型

1 引言

股市价量关系研究是技术分析的重要内容，也是金融领域研究的重点难点问题。我国投资者普遍认为2014-2015年的牛市是“水牛”，事实上，“水牛”说法包含价量因果关系特征——即交易量的提升拉动价格上涨，是资金推动型市场。但事实的确如此吗？诚然，在此轮牛市中价格上涨的同时伴随着交易量的巨量提升(见图1)，但仍须通过科学严谨的实证检验来识别我国股市价量关系特征。而且由于我国股市时常发生大幅波动，如2007-2008年和2014-2015年两次大涨大跌，价量关系可能会随时间变化而改变，以及受到市场波动的影响。为此，考察时间断点和市场波动性对价量关系的影响，对深入理解我国股市微观结构和价格波动传导机制，无疑具有重要理论和现实意义。

在理论上，价量关系定义为金融资产收益率与交易量的关系，其深刻反应了资产市场运行效率和信息动态[1]。Karpoff[1]和Gallent等[2]指出，以前的实证工作主要关注价格与交易量的同期关系，但对预测和风险管理而言，收益率与交易量间的动态(因果)关系包含更多信息[3]。

一些理论研究考察了股票收益率与交易量的动态(因果)关系。Copeland[4]和Jennings等[5]通过建立信息到达模型发现股票收益率与交易量间存在正的双向因果关系。在Epps和Epps[6]的混合分布模型中用交易量衡量交易商的价格分歧，交易商基于新进入市场的信息来修正其保留价格，模型表明从交易量到绝对收益具有正的因果关系。然而，在Clark[7]的混合共同因子模型中交易量被视作信息流速度的代理变量，在该模型中交易量与股票收益没有因果关系。Campbell等[8]指出伴随着高交易量的价格变动往往会被扭转，而那些交易量低的日内价格变动则不会出现此情况。此外，还有其他强调交易量信息内涵的均衡模型，Blume等[9]指出交易量提供了过去价格变动的信息，因此交易量用于解释价格(收益)的行为非常有用。Wang Jiang[10]在一个具有信息不对称特征的模型中发现交易量可能会提供关于未来预期收益的信息。Liu Xinghua等[11]也在信息不对称的代理人模型中发现信息驱动的交易会产生价量关系。翟爱梅和周彤[12]在基于市场参与者非理性行为假设的模型中发现成交量和成交价格的变动正相关，成交量和成交价格变动的绝对值正相关。

尽管有强大的理论基础，Karpoff[1]全面考察了支持价量间具有同期相关性的经验证据，仅发现二者间具有微弱的相互影响，Gallent等[2]也发现了类似结果。1990年以来，研究焦点开始转向股票收益与交易量间的动态(因果)关系，主要是基于格兰杰因果关系检验法的考察。但在这方面研究中，理论上“过去的交易量会对当前收益产生影响”的因果关系也没得到有力的实证支持。例如，Lee和Rui[13]指出中国沪深A股和B股市场的交易量并不能预测第二天收益。Chen Gongmeng等[14]指出在法国、意大利、日本、英国和美国市场中也不存在这样的因果关系。Lee和Rui[15]采用日度数据研究发现在美国、日本和英国股市中，交易量并不是收益率的格兰杰原因。在巴基斯坦市场[16]和五个东南亚新兴市场[17]中，交易量和收益率间也不存在因果关系。Azada等[18]考察了三个南亚新兴市场国家的价量关系，发现南亚金融市场处于弱的无效率形式。Chuang等[19]在其所分析的十个亚洲市场中，仅在两个市场中发现交易量能够影响收益率。Chen[20]指出S&P500的交易活动仅在熊市中能影响后来的收益率，但当同时考虑牛市和熊市时量价间因果关系就没有了。不过，也有一些研究发现交易量与收益率间存在因果关系，如Saatcioglu和Starks[21]和Rojas和Kristjanpoller[22]对六个拉美国家的研究。范从来和徐科军[23]指出中国股市的交易量在一定程度上可作为衡量不同时期公司股票收益率间领先关系的指标。张永冀等[24]研究发现交易量信息在中国股市的价格发现中比历史价格信息更有效。

还有一些研究指出价量间具有非线性关系[25-26]。Chuang等[3]使用分位数回归法研究发现对于NYSE、S&P500和FTSE100指数，当收益率处于分布顶端(底端)时，过去的交易量对收益率具有正向(负向)影响，Lin[27]和Gebka和Wohar[28]采用相同方法研究发现在六个亚洲新兴市场国家和太平洋盆地国家也存在此现象。钱争鸣和郭鹏辉[29]也采用分位数回归法研究发现中国股市价量关系存在明显的价格非对称性。许启发[30]等进一步采用大规模数据分位回归方法研究指令不均衡与股票收益的关系，发现指令不均衡对股票收益具有解释和预测能力。除了分位数回归法，学者们还采用其他非线性方法考察股市价量关系，如Matilla-Garcia等[31]利用基于排列熵的非参数检验法研究股票价格与交易量间的非线性因果关系，Hasan和Salim[32]运用碎形几何的非线性方法研究发现印度股市的价量交叉相关，而且价量间关联是复杂状态。此外，还有基于机制转换Copula模型研究股市量价尾部关系特征[33]、运用动态估计方法分析股市历史信息的长记忆性特征[34]以及运用ARMA-GJR-GARCH-Copula模型分析市场流动性与市场预期间的动态相关结构[35]等相关研究。

考察国内外相关文献不难发现：第一，无论是采用线性或非线性方法，已有研究都很少考察价量关系的结构变动特征，而这很可能对我国股市价量关系有显著影响，因为我国股市时常发生大涨大跌；第二，在我们的文献阅读范围内，已有研究没有考虑到市场不确定性对价量关系的影响。如果用交易量衡量投资者交易行为，那么价量关系即为投资者交易行为与市场价格间的双向互动关系，一方面，投资者根据其对未来价格的预期做出投资交易决策，另一方面，投资者交易行为也影响市场价格走势。在已有文献中，一个被忽视却十分重要的基本事实是——投资者是基于其对未来价格的预期而做出交易决策的，即投资者是在不确定的环境下做出交易决策，因此投资者将不仅考虑预期价格，也同样在乎价格的不确定性(即风险，可用波动率衡量)。在相同的预期价格下，不确定性的不同也可能导致投资者做出不同的投资交易决策，因此价量关系就会受到市场不确定性的影响。特别地，由于我国股市时常发生大幅波动，市场不确定性对价量关系的影响就显得更为重要。

本文通过采用门限VAR模型，在价量关系的VAR框架中嵌入结构变化和市场波动的门限变量，研究时间断点和市场波动率对我国股市价量关系的非对称影响。本文边际贡献主要包括：第一，本文在价量关系研究中首次将市场不确定性因素纳入考量，为价量关系研究提供了新视角，丰富了该领域的文献，同时也使研究结论更加贴近现实，是本文的重要创新点；第二，本文通过采用门限VAR模型，以市场波动率作为门限变量，研究波动水平对股市价量关系的门限效果；第三，本文从时间结构变化视角，采用结构变动VAR模型识别出了我国股市近十几年来价量关系发生显着突变的时间断点，有助于更好地理解我国股市价量关系的时变特征，在研究方法上具有一定创新性。

2 模型与方法

2.1线性VAR模型

价量关系具有明显的双向因果性，因此对价量关系建模会遇到内生性问题。Sims[36]提出的向量自回归模型(Vector Autoregression，简称VAR)通过将系统中每一个内生变量作为所有内生变量滞后值的函数来建立模型，是处理多个内生时间序列变量的有效工具。普通VAR模型假设变量间关系为线性，又称为线性VAR模型。

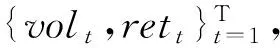
(1)

其中，Li为滞后算子，i=1，2，…，p。

2.2门限VAR模型

门限VAR模型(Threshold VAR，简称TVAR)是识别系统中非线性特征的拓展VAR模型，非线性特征可能来自于结构变动、非对称性等因素，对本文研究对象股市价量关系而言，意味着价量关系特征是否随着样本某一特征变量的变动而改变。这个特征变量，就是用来划分样本的门限变量(Threshold variable)。依据门限变量所设定的划分标准，称为门限值(Threshold value)。门限变量所捕捉到的模型非对称性，允许模型中的系数矩阵在门限值前后发生变动。门限变量既可以是VAR系统的内生变量，也可以是其他外生变量。门限值的设定可以是一个(或多个)，然后根据门限值将样本一分为二(或分成更多子样本)。

(2)

其中，I(·)为示性函数，若括号中表达式为真，则取值为1，反之为0。γ为待估计门限值。显然，TVAR模型是一个非线性VAR模型，因为它无法写成各参数的线性函数。TVAR模型的估计方法为最小化残差平方和(SSR)，通常使用两步法估计：第一步，给定γ的取值，对方程(2)使用线性回归方法来估计各系数，并计算残差平方和SSR(γ)，其为γ的函数；第二步，选择γ使SSR(γ)最小化，并据此得到估计系数。

Hansen[37]提出似然比检验法(LR test)来检验门限效应(Threshold effect)的显著性：

(3)

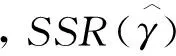
类似地，当包含两个门限值(γ1和γ2，γ1<γ2)时，TVAR模型可设定如方程(4)所示，其估计和检验方法也与上述类似。

(4)

可以看出，建立TVAR模型关键在于门限变量的选择，选择不同门限变量，模型估计结果及含义也不同。当选择时间作为门限变量(thvt=t)，可研究VAR模型结构的时间变动(Time varying)特征，此时模型又称作结构变动VAR模型(Structural change VAR，简称scVAR)。

2.3研究设计

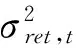
3 数据与描述性统计

3.1数据来源与处理

选择2003年3月4日到2016年6月24日的上证指数日收盘价pt和交易量Qt作为原始数据，样本观测数3213。对原始数据做如下处理：根据方程(5)计算出上证指数的日百分比收益率，作为调整后价格(rett)；根据方程(6)去除交易量的时间趋势，其中T为时间变量，取出回归残差项作为调整后交易量(volt)。

rett=[log(pt)-log(pt-1)]*100

(5)

log(Qt)=c+αT+ε

(6)

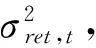
均值方程：rett=c+φrett-1+εt

(7)

(8)

3.2描述性统计分析

从图1可看出，上证指数价格与交易量变动存在明显正相关性，而且在2007-2008年和2014-2015年两次股市大幅波动期间尤其显著，但这两次股市波动期间的一个显著区别是：在2014-2015年伴随着价格上涨和下跌，交易量的变动幅度更大、更剧烈。此外，市场波动性呈现出明显集聚特征，波动率较高的区间主要集中在2007-2008年和2014-2015年，此时价格和交易量的变动性也较大，这很可能会导致价量关系特征发生突变。

表1为对变量的描述性统计。调整前后的价格均具有尖峰特征，调整前价格呈右偏态势，调整后价格呈左偏态势，但偏离程度已有所缓和；调整前交易量表现出右偏和尖峰态势，调整后交易量的右偏和尖峰程度已明显缓和；市场波动率也表现出一定程度的尖峰和右偏态势。J-B统计量均显著拒绝所有序列分布的正态性假设，说明在样本期间这些序列均为偏态分布。ADF统计量表明，调整后价格和交易量以及市场波动率均显著平稳，不具有单位根，满足VAR建模条件。

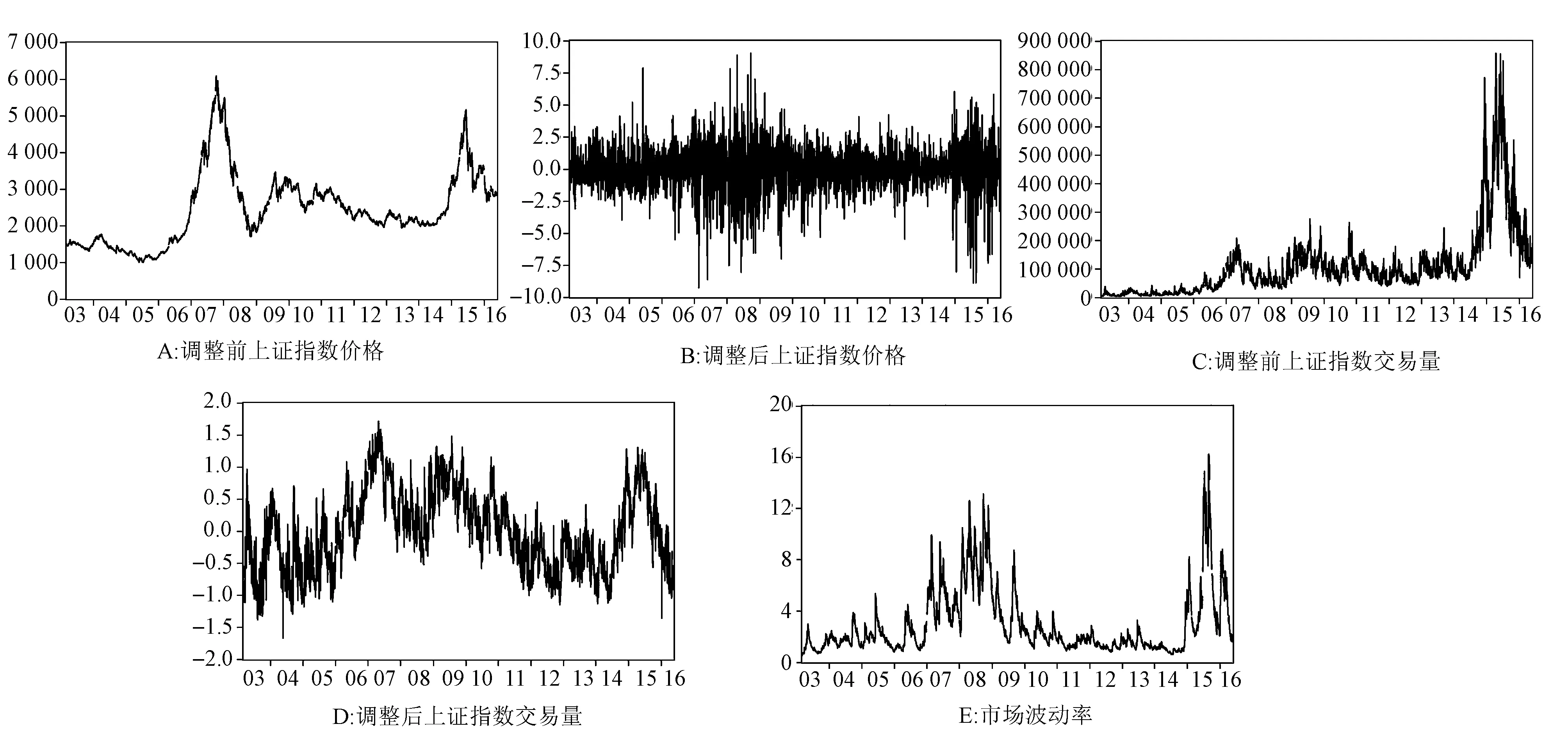
图1 变量时间序列图

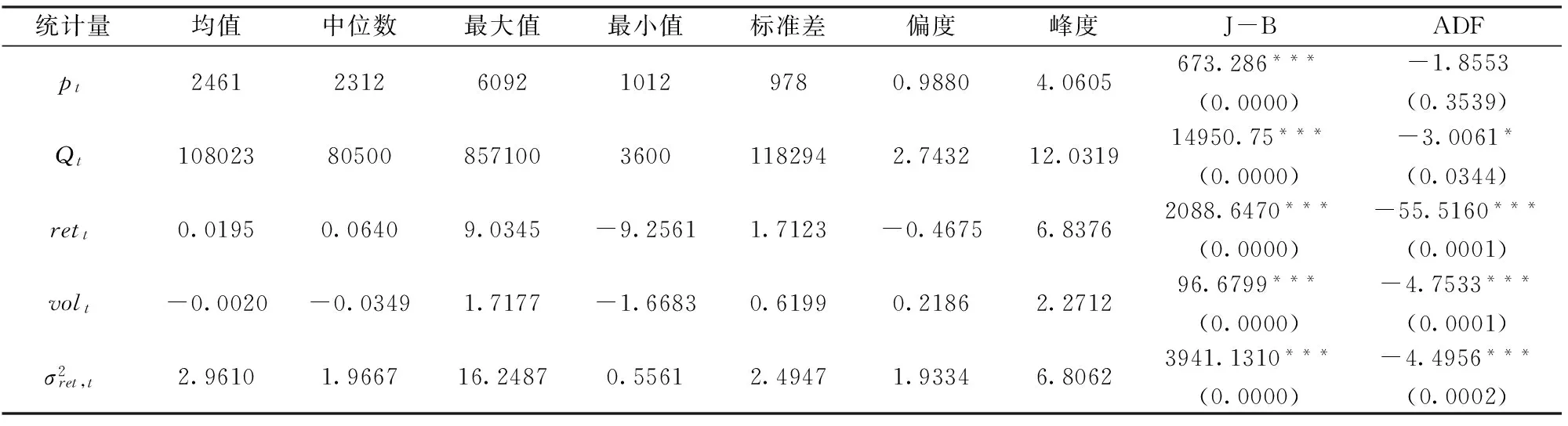
表1 描述性统计

注：括号内为p值，*、**和***分别表示在5%、1%和0.1%水平上显著，下同。

4 实证结果及分析

4.1中国股市价量关系的总体特征

依据施瓦兹信息准则(SIC)确定VAR模型最佳滞后阶数为4，建立VAR(4)模型。格兰杰因果关系检验结果(表2)显示，价格是交易量的格兰杰原因，在0.1%水平上高度显著；交易量也是价格的格兰杰原因，但仅在5%水平上显著，考虑到样本容量大，5%显著性不具有很强说服力。由此可推断，在2003-2016年我国股市中价格显著引导交易量的变动，而交易量对价格影响较弱。

表2 格兰杰因果关系检验结果(全样本区间)

4.2股市价量关系时间结构变动检验

4.2.1 时间门限值的估计

以时间为门限变量(thvt=t)建立scVAR模型，门限值选择过程见图2，图2-(a)为单个门限值选择过程，图2-(b)为两个门限值选择过程。估计和检验结果见表3-A。当设定单个门限值时，估计出的门限值为t=2015/6/12，scVAR系统中两条方程的LR统计量都在0.1%水平上显著拒绝“不存在门限效应”的原假设，说明在t=2015/6/12处存在显著门限效应；当设定两个门限值时，估计出的两个门限值分别为t1=2015/6/12和t2=2014/8/28，也通过了LR检验。

scVAR模型估计结果与我国股市行情走势十分吻合，t2和t1正好是2014-2015年牛市的起点和终点，2014年下半年牛市启动，一路上涨直到2015年6月12日上证指数创出5178的最高点，随后“股灾”发生。这说明我国股市价量关系在2014-2015期间发生了显著的结构变动。

t1和t2将原样本区间划分成2003/3/4-2014/8/28、2014/8/28-2015/6/12和2015/6/12-2016/6/24三个子区间。由于子区间2003/3/4-2014/8/28的时间跨度长，且包含一轮完整的牛熊循环，在此期间价量关系很可能也发生了较显著的结构变动。为此，在2003/3/4-2014/8/28区间内再次构建scVAR模型，因篇幅所限，门限值选择过程图示不再列出。估计和检验结果见表3-B，估计出的单个门限值为t′=2007/10/16，估计出的两个门限值分别为t3=2007/10/16和t4=2008/11/04，并通过LR检验，说明在t3和t4处也存在显著的门限效应。

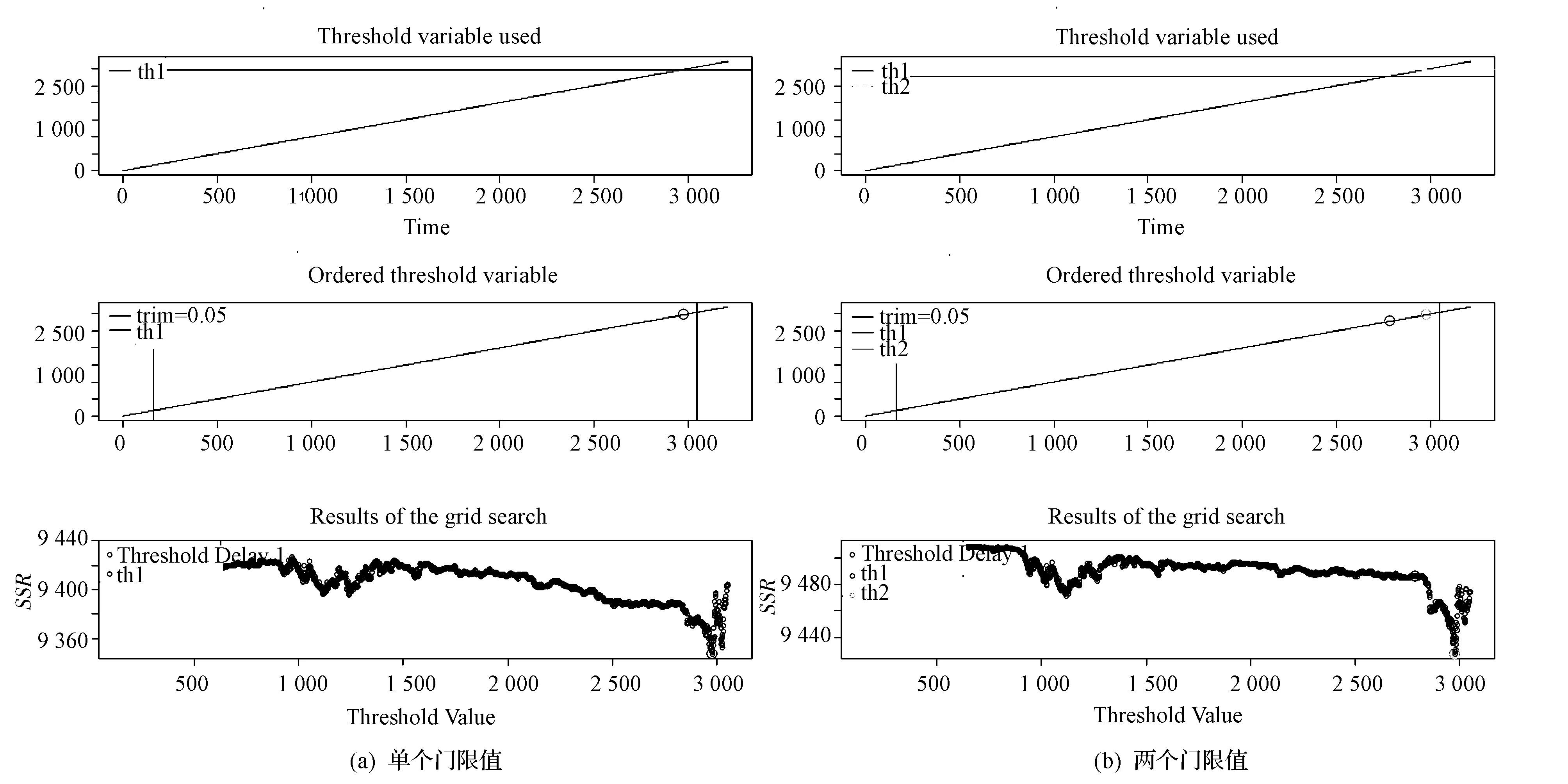
图2 时间门限值的选择过程 注：第一张图是门限变量的时间序列图，第二张图是对门限变量的排序，第三张图是格点搜索结果图，下同。

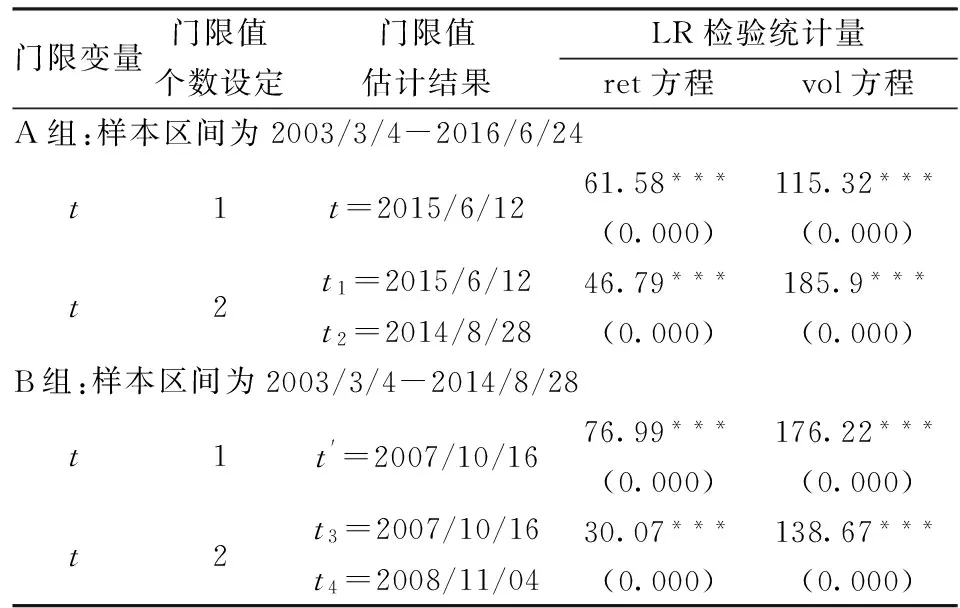
表3 scVAR模型的门限值估计结果

基于区间2003/3/4-2014/8/28的scVAR模型估计结果也与我国股市行情走势相当吻合，t3和t4两个门限值正好识别出2007-2008年的牛熊周期，在t3处，上证指数涨至历史最高点6124，随后开始暴跌，一路下跌至t4=2008/11/04处的最低点1707，之后长期低位徘徊。这说明我国股市价量关系在2007-2008年期间也发生了较显著的结构变动。

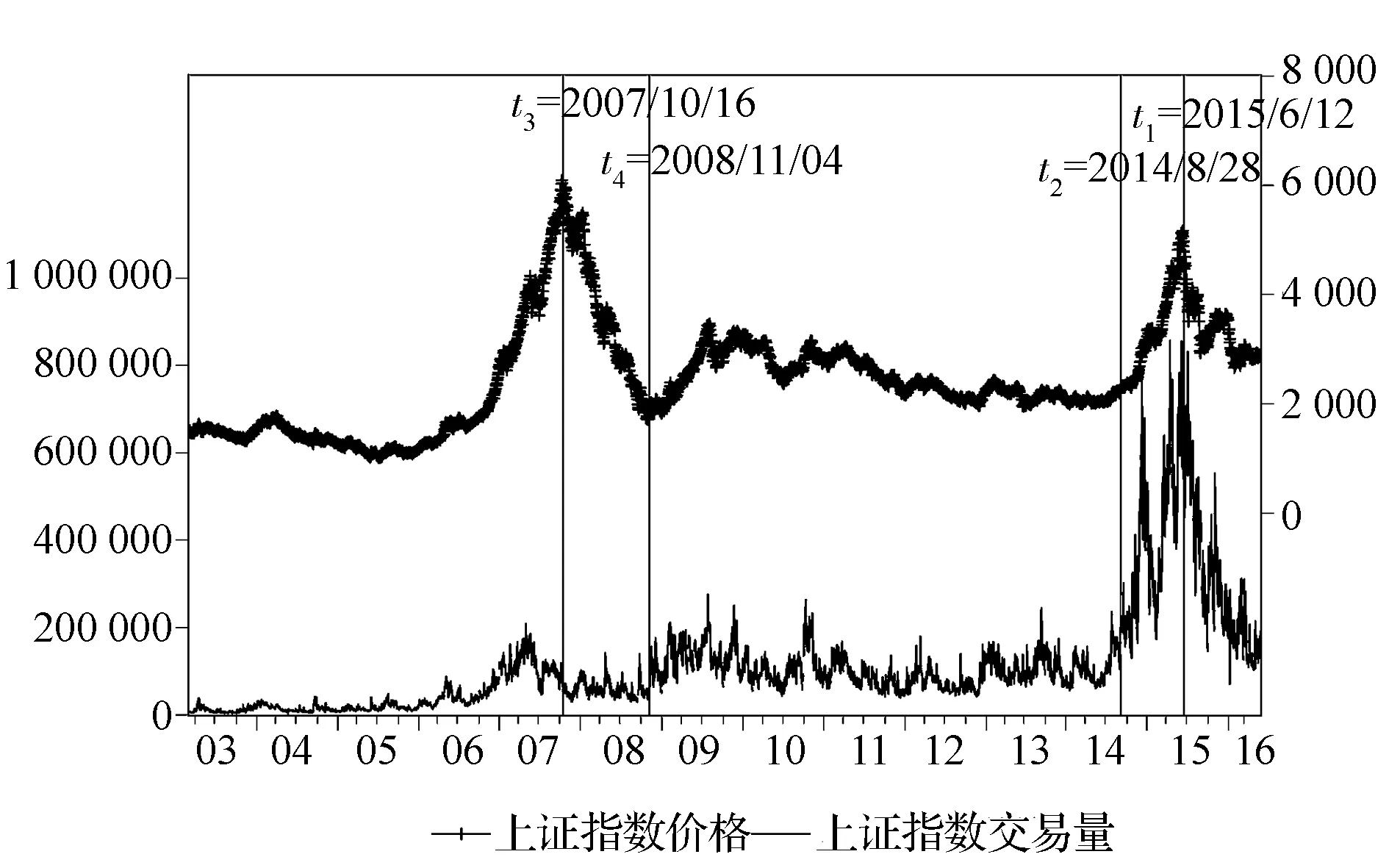
图3 基于scVAR模型识别出的时间门限值

至此已识别出t1、t2、t3和t4四个时间门限值(图3)，在这四个门限值上价量关系发生了显著结构变动。根据被识别出的先后顺序，易知发生结构变动的剧烈程度大小依次为t1>t2>t3>t4。据此可推断：第一，当股市达到高位后开始暴跌时，价量关系的结构变动效应更为剧烈(t1>t2，t3>t4)；第二，价量关系在2014-2015年的结构变动比在2007-2007年更剧烈(因为t1>t2>t3>t4)；第三，2014-2015年的价量关系结构变动特征与2007-2008年不同，2014-2015年价量关系的结构变动发生在股市大幅上涨阶段，伴随着价格上涨，交易量呈现出更大幅度的上涨和更剧烈的波动，但2007-2008年价量关系的结构变动发生在股市暴跌阶段，伴随着价格快速下跌，交易量变化却不明显。

4.2.2 股市价量关系结构变动的分区间检验

根据四个时间门限值将原样本划分为五个子区间，在各子区间内分别建立VAR模型。格兰杰因果关系检验结果(表4)显示，交易量仅在子区间1内是价格的格兰杰原因，即交易量仅在2007年股市暴跌前对价格有一定影响，此后交易量对价格再也没有显著影响；而除了在子区间5，价格对交易量的影响始终高度显著。

上述结果证明，我国股市中价格对交易量的影响远大于交易量对价格的影响，是价格拉动型而非资金推动型市场。在子区间4(2014-2015年牛市期间)，价格显著影响交易量，而交易量对价格没有任何影响，说明在此期间股价上涨并不是由交易量提升所致，相反，股价上涨拉动了交易量的提升，因此“水牛”说法并不准确。

表4 格兰杰因果关系检验结果(分区间)

4.3市场波动率对价量关系影响的非对称性检验

4.3.1 市场波动率门限值的估计

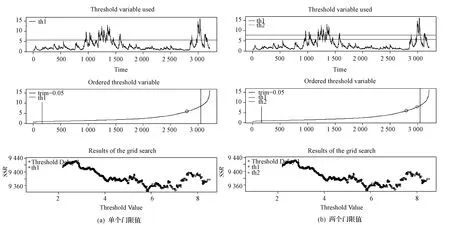
图4 市场波动率门限值的选择过程

表5 TVAR模型的门限值估计结果

4.3.2 市场波动率对价量关系非对称影响的检验

根据两个市场波动率门限值将样本划分为三个子区间。由于子区间观测值不连续，无法建立线性VAR模型并做格兰杰因果关系检验，因此本文通过比较TVAR系统中各变量的系数及显著性水平变化情况来研究市场波动率对价量关系的非对称影响。在TVAR(4)模型中，以滞后1到4期的价格和交易量作为解释变量，由于各滞后变量间具有较强自相关性，因此难以对所有滞后变量的系数和显著性做出合理解读。一般而言，前一天的价格和交易量对当天价格和交易量的影响较大，相隔天数越多，影响越小。也就是说，滞后1期的解释变量系数及显著性水平最具可信性和说服力，因此本文选择比较各子区间内滞后1期的价格和交易量的系数及显著性水平变动情况来检验市场波动性对价量关系的影响。

TVAR模型回归结果见表6。ret方程的系数变化情况：在区间1，vol(-1)的系数为0.3761，仅在5%水平上显著；在区间2和区间3，vol(-1)的系数已不显著。vol方程的系数变动情况：在区间1，ret(-1)的系数为0.0419，在0.1%水平上高度显著；在区间2和区间3，ret(-1)的系数分别下降为0.0197和0.018，但仍都在0.1%水平上高度显著。

因此可推断，交易量仅在市场波动性低时才对价格产生微弱影响，而价格对交易量一直具有十分显著的影响。随着市场波动性提高，交易量对价格的影响逐渐消失，而价格对交易量的影响始终高度显著，但经济显著性也逐渐下降。上述发现证实了本文最初的猜想——市场不确定性对价量关系具有显著影响，因为投资者是在不确定的环境下做出交易决策，投资者交易决策不仅受到未来预期价格的影响，还受到价格不确定性的影响。

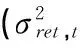
表6 TVAR模型回归结果为门限变量)

注：最佳滞后阶数p=4根据SIC准则确定。括号内为标准误，*、**和***分别表示在5%、1%和0.1%水平上显著。

5 结语

由于价量同期内生问题，股市价量关系实证研究通常在VAR框架下进行，但利用线性VAR方法考察价量关系没有考虑到结构变动和市场波动性的影响，而这在我国股市中是十分重要的因素。本文通过在价量关系VAR框架中嵌入结构变化和市场波动的门限变量来估计我国股市价量关系的动态变化，在文献上具有重要贡献。本文研究发现了稳健的结果和有意义的推论：第一，我国股市价量关系在2007-2008年和2014-2015年期间存在显著的时间断点效应，且后者结构变化更剧烈。第二，市场波动率显著影响价量关系，当市场波动性低时，交易量与价格相互影响，但价格对交易量影响更大；随着波动性提高(主要是在2007-2008年与2014-2015年期间)，交易量对价格的影响逐渐消失，而价格对交易量的影响仍十分显著，但经济显著性逐渐下降。第三，总体来看，我国股市中价格显著引导交易量的变动，而交易量对价格的影响十分微弱，可见我国股市是价格拉动型而非资金推动型市场，因此“水牛”说法并不准确。

本文结论纠正了当前关于“水牛”的错误认知，对理解我国股市微观结构及其变动特征具有重要意义，有助于投资者增强技术分析有效性，提升股市预测能力和风险管理水平。对监管层而言，本文政策含义在于，监管层应不断提升股市管理水平，加强股市风险预警与监控，避免出现单边市的暴涨暴跌，维护股市平稳健康发展。一旦股市出现异常波动，救市要趁早，因为在市场大幅波动期间价量关系极弱，此时试图通过市场介入方式来救市，效果微弱且成本高昂。

[1] Karpoff J M.The relation between price changes and trading volume: A survey[J].Journal of Financial and quantitative Analysis,1987,22(01): 109-126.

[2] Gallant A R,Rossi P E,Tauchen G.Stock prices and volume[J].Review of Financial Studies,1992,5(2): 199-242.

[3] Chuang C C,Kuan C M,Lin H Y.Causality in quantiles and dynamic stock return-volume relations[J].Journal of Banking &Finance,2009,33(7): 1351-1360.

[4] Copeland T E.A model of asset trading under the assumption of sequential information arrival[J].The Journal of Finance,1976,31(4): 1149-1168.

[5] Jennings R H,Starks L T,Fellingham J C.An equilibrium model of asset trading with sequential information arrival[J].The Journal of Finance,1981,36(1): 143-161.

[6] Epps T W,Epps M L.The stochastic dependence of security price changes and transaction volumes: Implications for the mixture-of-distributions hypothesis[J].Econometrica,1976: 305-321.

[7] Clark P K.A subordinated stochastic process model with finite variance for speculative prices[J].Econometrica,1973: 135-155.

[8] Campbell J Y,Grossman S J,Wang Jiang.Trading volume and serial correlation in stock returns[J].The Quarterly Journal of Economics,1993,108(4): 905-939.

[9] Blume L,Easley D,O'hara M.Market statistics and technical analysis: The role of volume[J].The Journal of Finance,1994,49(1): 153-181.

[10] Wang Jiang.A model of competitive stock trading volume[J].Journal of political Economy,1994,102,(1): 127-168.

[11] Liu Xinghua,Liu Xin,Liang Xiaobei.Information-driven trade and price-volume relationship in artificial stock markets[J].Physica A: Statistical Mechanics and its Applications,2015,430: 73-80.

[12] 翟爱梅,周彤.基于市场参与者行为假设的股票市场量价关系研究[J].中国管理科学,2011,19(04):31-37.

[13] Lee C F,Rui O M.Does trading volume contain information to predict stock returns? Evidence from China's stockmarkets[J].Review of Quantitative Finance and Accounting,2000,14(4): 341-360.

[14] Chen Gongmeng,Firth M,Rui O M.The dynamic relation between stock returns,trading volume,and volatility[J].Financial Review,2001,36(3): 153-174.

[15] Lee B S,Rui O M.The dynamic relationship between stock returns and trading volume: Domestic and cross-country evidence[J].Journal of Banking &Finance,2002,26(1): 51-78.

[16] Rashid A.Stock prices and trading volume: An assessment for linear and nonlinear Granger causality[J].Journal of Asian Economics,2007,18(4): 595-612.

[17] Pisedtasalasai A,Gunasekarage A.Causal and dynamic relationships among stock returns,return volatility and trading volume: Evidence from emerging markets in South-East Asia[J].Asia-Pacific Financial Markets,2007,14(4): 277-297.

[18] Azad A S M S,Azmat S,Fang V,et al.Unchecked manipulations,price-volume relationship and market efficiency: Evidence from emerging markets[J].Research in International Business and Finance,2014,30: 51-71.

[19] Chuang W I,Liu H H,Susmel R.The bivariate GARCH approach to investigating the relation between stock returns,trading volume,and return volatility[J].Global Finance Journal,2012,23(1): 1-15.

[20] Chen S S.Revisiting the empirical linkages between stock returns and trading volume[J].Journal of Banking &Finance,2012,36(6): 1781-1788.

[21] Saatcioglu K,Starks L T.The stock price-volume relationship in emerging stock markets: The case of Latin America[J].International Journal of forecasting,1998,14(2): 215-225.

[22] Rojas E,Kristjanpoller W.Price-volume ratio analysis by causality and day-of-the-week effect for the Latin American stock markets[J].Lecturas de Economía,2015(83): 9-31.

[23] 范从来,徐科军.中国股票市场收益率与交易量相关性的实证分析[J].管理世界,2002,(07): 31-36.

[24] 张永冀,汪昌云,华晨.历史价量信息在价格发现中更有效吗?——基于中国证券市场的数据分析[J].中国管理科学,2013,21(S1):346-354.

[25] Hiemstra C,Jones J D.Testing for linear and nonlinear Granger causality in the stock price-volume relation[J].The Journal of Finance,1994,49(5): 1639-1664.

[26] Caginalp G,DeSantis M.Does price efficiency increase with trading volume? Evidence of nonlinearity and power laws in ETFs[J].Physica A: Statistical Mechanics and its Applications,2017,467: 436-452.

[27] Lin H Y.Dynamic stock return-volume relation: Evidence from emerging Asian markets[J].Bulletin of Economic Research,2013,65(2): 178-193.

[28] Gebka B,Wohar M E.Causality between trading volume and returns: Evidence from quantile regressions[J].International Review of Economics &Finance,2013,27: 144-159.

[29] 钱争鸣,郭鹏辉.上海证券交易市场量价关系的分位回归分析[J].数量经济技术经济研究,2007,(10): 141-150.

[30] 许启发,蔡超,蒋翠侠.指令不均衡与股票收益关系研究——基于大规模数据分位数回归的实证[J].中国管理科学,2016,24(12):20-29.

[31] Matilla-García M,Marín M R,Dore M I.A permutation entropy based test for causality: The volume-stock price relation[J].Physica A: Statistical Mechanics and its Applications,2014,398: 280-288.

[32] Hasan R,Salim M M.Power law cross-correlations between price change and volume change of Indian stocks[J].Physica A: Statistical Mechanics and its Applications,2017,473: 620-631.

[33] 吴吉林.基于机制转换Copula模型的股市量价尾部关系研究[J].中国管理科学,2012,20 (05): 16-23.

[34] 李云红,魏宇,张帮正.股票市场历史信息的长记忆性特征研究[J].中国管理科学,2015,23(09):37-45.

[35] 姚登宝,刘晓星,张旭.市场流动性与市场预期的动态相关结构研究——基于ARMA-GJR-GARCH-Copula模型分析[J].中国管理科学,2016,24(02):1-10.

[36] Sims C A.Macroeconomics and reality[J].Econometrica,1980,48(1): 1-48.

[37] Hansen B.Testing for linearity[J].Journal of Economic Surveys,1999,13(5): 551-576.

Abstract： In literature,the dynamic price-volume relation is examined by Vector Autoregression (VAR thereafter) model.In this paper,the conventional VAR approach is extended to account for the impacts of structural changes and volatility levels,which are common to China.Due to dramatic responses of China’s stock market in recent years,especially two periods of considerable volatility in the years of 2007-2008 and 2014-2015,it is reasonable to conjecture that the structural changes and volatility levels could have substantial influence on the price-volume relation of Chinese stock market.The price-volume relation of the Shanghai stock market is examined with daily data from the year of 2003 to 2016,and contribution is made to the literature by estimating the price-volume relation in a VAR framework with structural breaks and volatility thresholds.As a result,more evidence and robust inferences is obtained: First,the evidence indicates that there exist significant time breaking effects.Second,the high-low volatility effects are substantially.Finally,a linear causal relation is identified from price to volume,which clearly rejects the public views.

Keywords： price-volume dynamics;structure change;market uncertainty;threshold VAR

The Price-Volume Relation of the Shanghai Stock Index Under the Perspective of Uncertainty

SHIJian-xun1,2,WANGPan-pan1,2,HeZong-wu3

(1.School of Economics and Management,Tongji University,Shanghai 200092,China；2.Institute of Finance and Economics,Tongji University,Shanghai 200092,China；3.Department of Finance,Shih Hsin University,Taipei 11645,China)

F830.9

A

1003-207(2017)09-0071-10

10.16381/j.cnki.issn1003-207x.2017.09.009

2016-08-25；

2017-03-22

国家社科基金决策咨询点研究项目(13JCD009)；国家社科基金一般项目(10BGJ019)；上海高校智库内涵建设计划项目

王盼盼(1993-)，男(汉族)，安徽舒城人，同济大学经济与管理学院博士生，同济大学财经研究所助理研究员，研究方向：金融市场理论与实践、金融计量，E-mail：panpan@tongji.edu.cn.