墙体材料理论湿渗透模型与应用分析
万 航 徐新华 严 天
墙体材料理论湿渗透模型与应用分析
万 航 徐新华 严 天
(华中科技大学环境科学与工程学院 武汉 430074)
在室内外环境的影响下,墙体内存在热湿传递。建立了单层墙体材料(或调湿材料)理论湿渗透模型并对模型进行了求解。计算出了常用不同建筑材料在不同湿周期作用下的理论湿渗透厚度。计算结果表明理论湿渗透厚度随环境湿变化周期增大而增大,同时不同建筑材料的理论湿渗透厚度也差异很大。在计算墙体与室内湿交换的模型中,等效湿渗透模型应用较广泛。但该模型基于材料不被穿透的假设获得的,理论湿渗透厚度可用来检查等效湿渗透模型的有效性。该理论厚度也可作为调湿材料厚度设计时的参考。
理论湿渗透厚度;等效湿渗透厚度;调湿材料
0 引言
建筑围护结构通常存在温度和湿度梯度,其热湿表现对空调负荷有不可忽视的影响[1,2],许多学者进行了很多研究。Moon等[3]将热湿模型和纯导热模型模拟结果进行对比,结果发现忽略湿传递会低估制冷与制热能耗,同时墙体的吸湿性作用会显著降低室内相对湿度的波动,维持室内湿度的稳定。墙体的这种湿缓存作用促使人们将调试材料应用于空调房间。研究结果表明,使用了调湿材料的空调房间的供热和制冷能耗可减少5%-30%[4,5]。
调湿材料能改善热舒适性,节约能源,延长围护结构的寿命,但墙体的湿传递受室内外环境等多种因素影响,过程复杂,导致其对空调负荷的影响难以定量化[6]。对于墙体外表面的湿过程,部分学者进行了试验及数值模拟研究。Labat等人[7]对6种不同的木结构墙体在实际气候条件下的热湿过程进行了测量与分析,结果表明对于由吸湿性较差的建筑材料组成的墙体,室外气候通过墙体对室内的湿度影响可以忽略不计。Steeman等[8]模拟对比分析研究指出,在计算空调负荷时可以将墙体外表面视作不可渗透。
由于围护结构及空调设备等的作用,室内环境相较室外更加稳定,室内相对湿度变化范围较小。文献[9]研究表明无论是空调房间还是非空调房间,绝大多数时间的室内相对湿度基本在40%-70%之间,而人体一般在湿度小于60%时才感到舒适[10]。以全年范围来看,室内相对湿度呈季节性变化,短时间内,可看作以日周期为变化。对于空调房间,日周期作用占主导地位。作为房间的调湿材料或者作为墙体内表面能起到湿度调节功能的建筑材料,在进行设计时应充分考虑材料的厚度。本文建立了墙体材料的理论湿渗透模型,并研究分析在不同周期性条件下墙体材料湿渗透厚度,并进一步给出了相关应用分析。
1 理论湿渗透模型
建筑材料的湿传递研究中有用含水量作为驱动势的[11-13],也有仅仅考虑水蒸气的扩散传递而忽略液态水的[14,15]。在材料的含水率低于其固有含水率,即不存在多孔体渗透时,多孔材料中的水分传导以水蒸气扩散占绝对主导地位,可以忽略液态扩散运动[11,16]。在墙体材料湿渗透模拟过程中,温度对材料的湿物性参数影响较小,可以忽略[17]。当相对湿度不超过90%时,水蒸气流占主导地位。因此湿驱动势可以选择水蒸气分压力,扩散系数可以归一化为一个综合系数[18]。
根据以上分析,对室内空气与墙体内表面的吸放湿过程作如下假设:室内温度波动较小,墙体视作等温;室内湿度变化范围较小(30%~80%),墙体含湿量在索态之下,蒸汽扩散占主导地位,忽略液态水传导;墙体材料湿物性参数为定值,如湿扩散系数,湿容,墙体表面质交换系数等;水蒸气分压力作为湿的驱动力;湿传递为一维传湿。基于以上假设,墙体内表面吸放湿的控制方程如式(1),空气中水蒸气扩散系数如式(2)。水蒸气分压不易直接测量,可用水蒸气浓度表示水蒸气分压,如式(3)及式(4)。
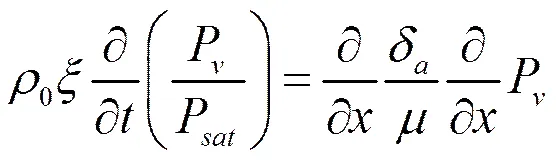
(2)
(3)
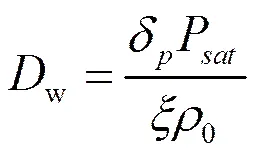
建筑围护结构墙体湿传递方程的初始条件及边界条件如式(5)及式(6)。
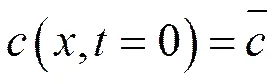
(6)
式中:=h/δ,c()=+c*sin();为角频率,s-1;h为墙体表面湿交换系数,kg/(Pa∙s∙m2);c为水蒸气浓度变化幅值,kg/m3;为水蒸气初始浓度,kg/m3;c为墙体表面水蒸气浓度,kg/m3。
根据初始条件及边界条件对式(1)求解,可获得墙体内或墙体材料内任意一点的湿分布,如式(7)所示。理论湿渗透厚度(Theoretical moist penetration depth,TMPD)可以定义为其值为某点的相对湿度变化幅值为材料表面相对湿度变化幅值1%时,此点离材料表面的距离[19]。式(7)简化为式(8),并进一步求出理论湿渗透厚度为式(9)。
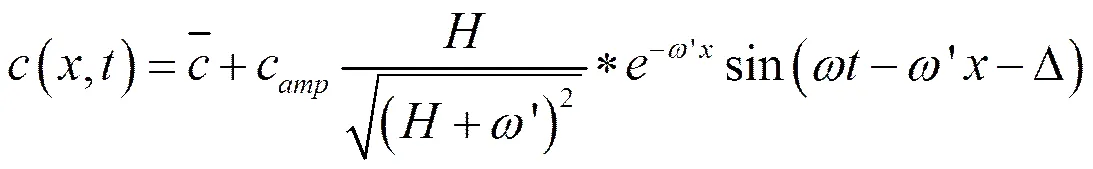
(8)
(9)
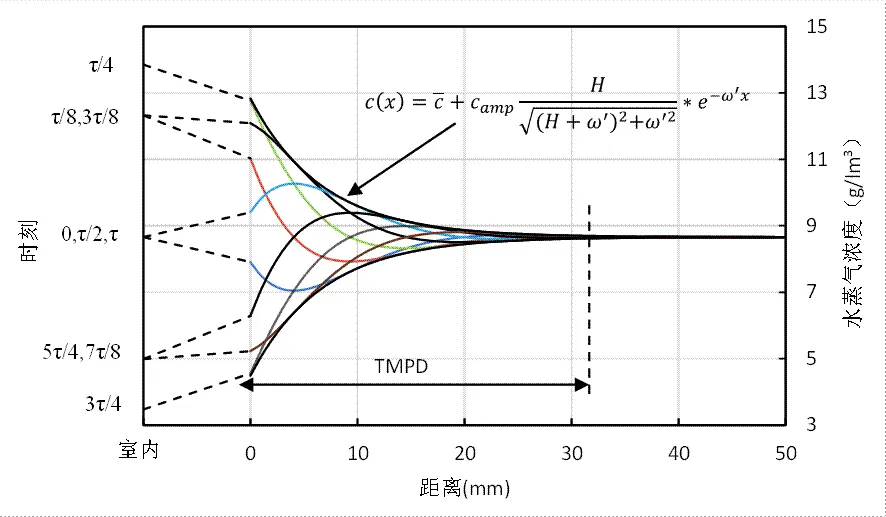
图1 周期作用下半无限大墙体材料内水蒸汽浓度分布图
由式(9)可以看出,理论湿渗透厚度随环境湿度变化周期增长而增大,季节性湿变化的理论湿渗透厚度远大于日湿变化的理论湿渗透厚度。当室内湿度变化周期一定时,墙体材料理论湿渗透厚度只取决于材料的导湿系数。图1为室内湿度24h周期变化条件下半无限大墙体材料内不同时刻水蒸汽浓度分布情况。由图可知,墙体表面水蒸气浓度振幅小于室内水蒸气浓度振幅,湿度波在墙体内的衰减较快,湿交换主要发生在材料表面附近的薄层内。
2 不同材料的理论渗透厚度
许多研究者对常用建筑材料的热湿特性参数进行了大量的测试[20-22]。本文选取几种常用建筑材料[20,22]进行分析。这些材料分别为加气混凝土、多孔混凝土、普通混凝土、石膏板1、石膏板2、石膏板3、普通砖、石灰石英砖、高密板1、高密板2、普通木板、巴沙木、松木、EPS板、XPS板。其湿物性参数如表1所示。本文对这些材料在表面含湿量变化周期分别为1小时,24小时,1周,1月时的理论湿渗透厚度进行计算,如表1。室内湿度变化周期为1个月时墙体材料理论湿渗透厚度是室内湿变化周期约为1天时的5.5倍,对于常用建筑围护结构材料如普通砖,EPS板,其月理论湿渗透厚度分别达到22厘米和38厘米,在更长周期如季节性湿变化条件下,墙体将会被湿穿透。
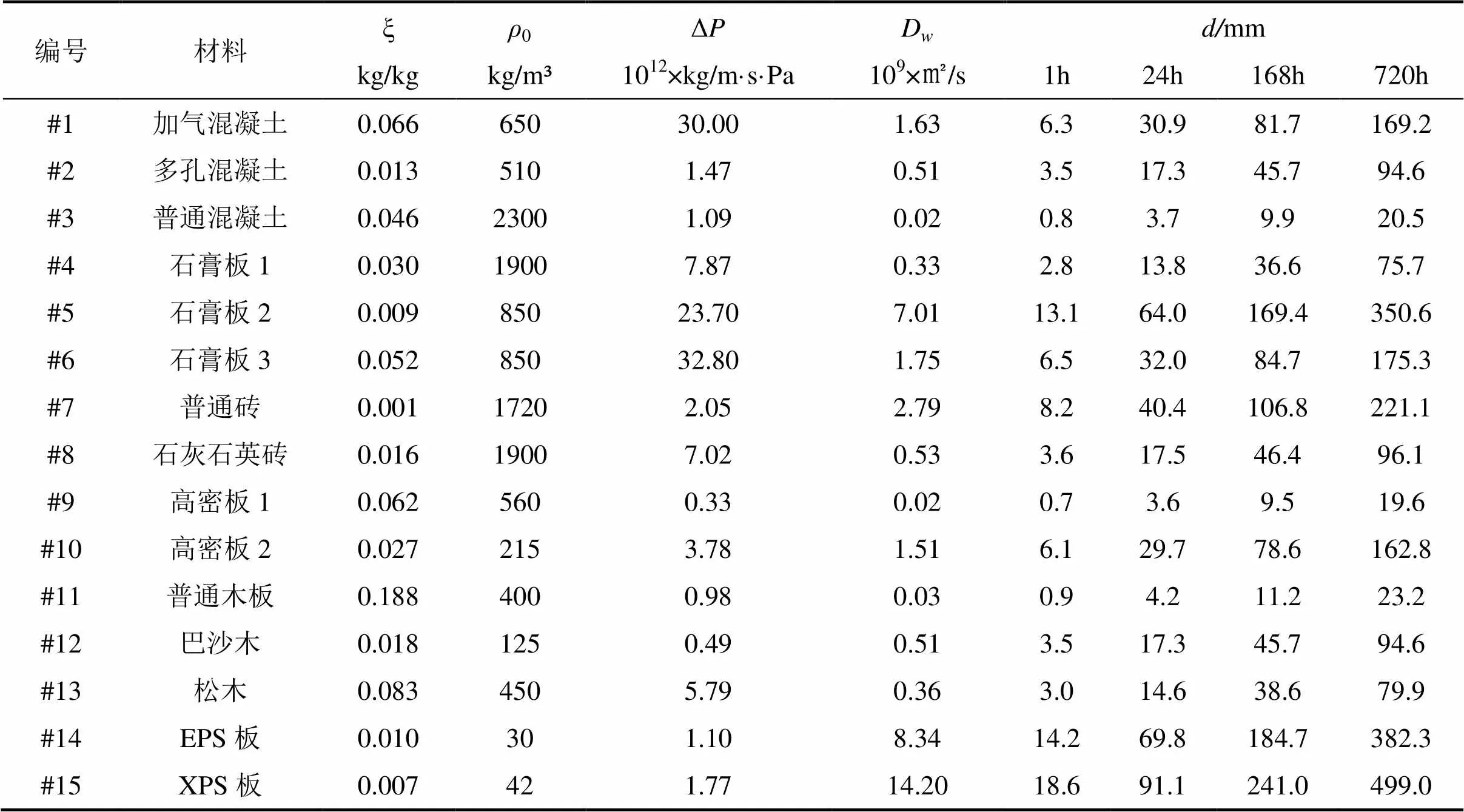
表1 墙体材料湿物性参数及理论湿渗透厚度
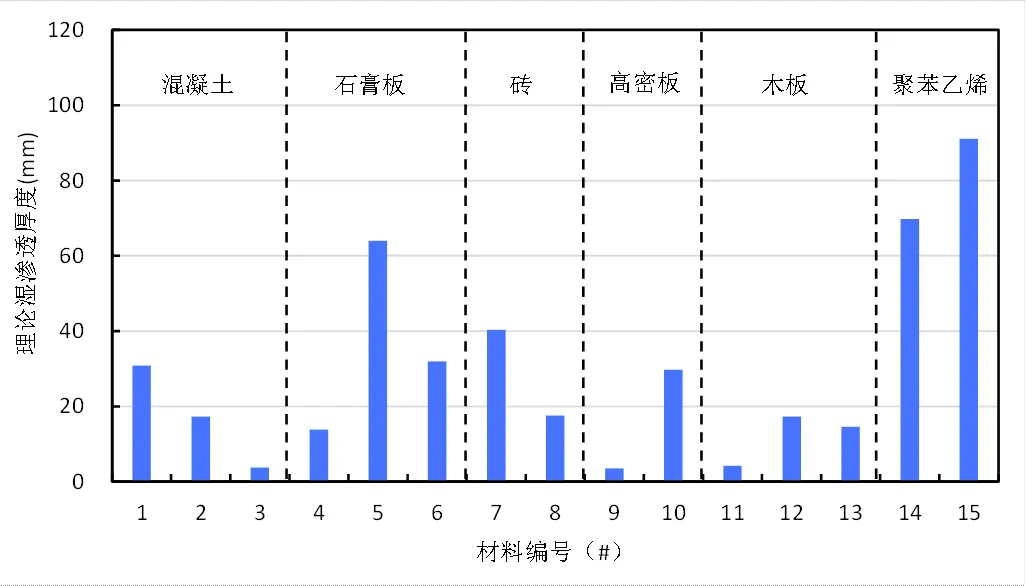
图2 不同材料日周期理论湿渗透厚度
当室内湿度变化周期为24小时时,各材料湿渗透厚度如图2所示。不同材料之间理论湿渗透厚度相差很大,同种类别不同形式的材料间相差也较大,这是由不同材料湿物性参数不同造成。石膏的理论湿渗透厚度较大,这是由于石膏的湿扩散系数较大,易于水蒸气在材料中的扩散,同时石膏的体积湿容较小,水蒸气在扩散过程中不易被吸收。与此相反,木头的体积湿容较大,同时湿扩散系数较小,导致木头的理论湿渗透厚度较小。聚苯乙烯理论湿渗透厚度较大是由于其密度较小导致导湿系数较大,较易被湿渗透,作为保温材料易产生结露与霉变[23]。
3 实际应用分析
保温材料越厚其保温隔热性能越好,同时成本也增加较多,不同气候区不同材料有不同的最佳保温厚度[24]。与保温材料类似,具有调节性能的建筑材料与调湿材料也应有最佳调湿厚度。根据节分析,木材的理论湿渗透厚度较小,湿容大,有一定的调湿作用。石膏的理论渗透厚度较大,湿容适中,湿缓存量大,湿扩散系数较大,吸放湿反应迅速,适合作为调湿材料。
80年代末,Cunningham[25]和Kerestecioglu[26]提出了等效湿渗透模型(EMPD-model)。该模型假设多孔材料与周围空气的湿交换仅发生在表面的薄层且该薄层的湿分布是均匀的。该薄层的厚度即为等效湿渗透厚度,该定义是基于半无限大墙体材料周围空气相对湿度为日周期变化时进行计算的,如式(10)。
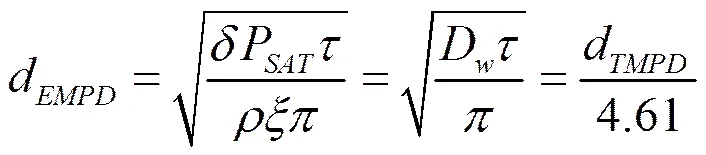
墙体材料的理论湿渗透厚度是等效湿渗透厚度的4.61倍。在考虑到等效湿渗透厚度模型使用时,材料的实际厚度应大于同周期下的理论渗透厚度,或者是等效湿渗透厚度的4.61倍。对于一个月一年的外界空气湿变化,墙体材料的理论湿渗透厚度都较大,以普通砖和石膏板为例,普通砖季(90天)理论湿渗透厚度约为3.64米,一般的实际厚度为0.24米、0.37米和0.49米,石膏板的月湿渗透厚度为0.96米,一般的实际厚度为0.02米和0.03米,普通砖在季周期、石膏板在月周期作用下已被湿穿透。按照等效湿渗透模型的形式采用一个月或一季度的周期进行计算长期等效湿渗透厚度[27],此时该模型并不适用。对于日周期也是这样,当日周期湿变化穿透了墙体材料时,等效湿渗透模型也不适用。
作为墙体调湿材料的厚度选型,应用日周期为主,同时也应兼顾较长周期的情况,比如非空调房间的季节性室内湿度调节。
4 结论
本文分析了建筑墙体材料所处的热湿环境,建立了墙体材料理论湿渗透模型,求解了在周期湿作用条件下不同时刻墙体材料内的湿分布,并给出了常用材料在不同周期下的理论湿渗透厚度。结果表明,不同墙体材料的理论湿渗透厚度相差较大,同一材料理论湿渗透厚度随周围空气湿变化周期增长而增大,月湿渗透厚度一般为日湿渗透厚度的5.5倍,在日周期下湿交换仅发生在材料表面薄层内,但在更长周期情况下墙体可能被湿穿透。墙体材料的理论湿渗透厚度是等效湿渗透厚度的4.61倍,如果墙体材料的实际厚度小于理论湿渗透厚度,即墙体被湿穿透,此时,以表面薄层湿均匀分布代替整个墙体材料湿分布的等效湿渗透模型便不再适用,等效湿渗透厚度需根据墙体材料实际厚度重新计算。墙体材料理论湿渗透厚度不仅可以用来检测等效湿渗透模型的适用性,同时可以作为调湿材料经济性厚度的参考,因此在建筑设计与节能应用中提供重要参考。
[1] Bailey D W, Bauer F C, Slama CF, et al. Investigation of dynamic latent heat storage effects of building construction and furnishings[R]. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta, GA (United States), 1996.
[2] Janssens A, De Paepe M. Effect of moisture inertia models on the predicted indoor humidity in a room[C]. Proceedings of the 26th AIVC conference, Brussels, 2005:287-294.
[3] Moon H J, Ryu S H, Kim J T. The effect of moisture transportation on energy efficiency and IAQ in residential buildings[J]. Energy and Buildings, 2014,75:439-446.
[4] Simonson C J, Salonvaara M, Ojanen T. Improving indoor climate and comfort with wooden structures, VTT-Report 2001[R]. Technical Research Centre of Finland, 2001.
[5] Simonson CJ, Salonvaara M, Ojanen T. Moderating indoor conditions with hygroscopic building materials and outdoor ventilation[J]. ASHRAE Transactions, 2004,110(2):804-819.
[6] Yang X, Fazio P, Ge H, et al. Evaluation of moisture buffering capacity of interior surface materials and furniture in a full-scale experimental investigation[J]. Building and Environment, 2012,47:188-196.
[7] Labat M, Woloszyn M, Garnier G, et al. Dynamic coupling between vapour and heat transfer in wall assemblies: Analysis of measurements achieved under real climate[J]. Building and Environment, 2015,87: 129-141.
[8] Steeman M, Goethals K, Laverge J, et al. On modelling moisture buffering when evaluating humidity controlled HVAC systems[C]. The 11th International Building Performance Simulation Association Conference, 2009: 819-826.
[9] CDH Energy Corp and Building Science Corp. Analysis of indoor environmental data, Research Report-0601[R]. http://buildingscience.com/sites/default/files/migrate/pdf/BA-0601_Indoor_Environment.pdf, 2006.
[10] Tanabe S, Kimura K. Effects of air temperature, humidity, and air movement on thermal comfort under hot and humid conditions[R]. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta, GA (United States), 1994.
[11] Luikov A V. Heat and mass transfer in capillary-porous bodies. Advances in heat transfer[J], 1964,1:123-184.
[12] Holm AH, Kuenzel HM. Practical application of an uncertainty approach for hygrothermal building simulations-drying of an AAC flat roof[J]. Building and environment, 2002,37(8):883-889.
[13] Korjenic A, Bednar T. An analytical solution of a moisture transfer problem for coupled room and building component[J]. Energy and Buildings, 2012,47:254-259.
[14] 陈友明,陈在康.建筑围护结构线性热湿同时传导方程的频域解法[J].应用基础与工程科学学报,1998,6(4): 367-382.
[15] Chen YM, Wang SW. Transfer function model and frequency domain validation of moisture sorption in air-conditioned buildings[J]. Building and Environment, 2001,36(5):579-588.
[16] Philip JR, De Vries DA. Moisture movement in porous materials undertemperature gradients[J]. Transactions American Geophysical Union, 1957,38:222-232.
[17] Krus M. Moisture transport and storage coefficients of porous mineral building materials: Theoretical principles and new test methods [M]. Fraunhofer IRB Verlag, 1996.
[18] Kwiatkowski J. Moisture in buildings air-envelope interaction [D]. Institut National des Sciences Appliquées de Lyon, 2009.
[19] Arfvidsson J. Moisture penetration depth for periodically varying relative humidity at the boundary[J]. CIB REPORT, 2000:75-80.
[20] Kerestecioglu A, Swami M, Dabir R, et al. Theoretical and computational investigation of algorithms for simultaneous heat and moisture transport in buildings. Florida Solar Energy Center[R]. Report FSEC-CR-191- 88, 1988.
[21] Rode C, Peuhkuri RH, Mortensen LH, et al. Moisture buffering of building materials[R]. Technical University of Denmark, Department of Civil Engineering, 2005.
[22] Li KS, Zhang X, Gao J. Experimental investigation of hygrothermal parameters of building materials under isothermal conditions[J]. Journal of Building Physics, 2009,32(4):355-370.
[23] 张文江,冯谦.EPS外墙外保温结露隐患的分析及应对策略[J].建筑节能,2007,35(8):18-19.
[24] 李春娥,韩喜莲,蔡颖.基于DeST模拟的外墙经济保温层厚度的分析[J].制冷与空调,2015,(1):60-63.
[25] Cunningham MJ. Effective penetration depth and effective resistance in moisture transfer[J]. Building and Environment, 1992,27(3):379-386.
[26] Kerestecioglu A, Swami M, Kamel A. Theoretical and computational investigation of simultaneous heat and moisture transfer in buildings: effective penetration depth theory[J]. ASHRAE Transactions, 1990,96(1):447-454.
[27] Klein SA. TRNSYS:Volume 6 Multizone Building modeling with Type56 and TRNBuild. version 16[J]. Madison, University of Wisconsin, 2006.
Theoretical Moisture Penetration Depth Model of Building Wall Material and its Application Analysis
Wan Hang Xu Xinhua Yan Tian
( School of Environment Science & Engineering, Huazhong University of Science andTechnology, Wuhan, 430074 )
Thermal and moisture transfer exists in building wall due to the disturbances of indoor environment and ambient. This paper present the theoretical moisture penetration model (TMPD-model) of a single-layer building material and its solution. The theoretical moisture penetration depths are presented for various conventional building materials under different moisture periods. The results show that the theoretical moisture penetration depth increases with the moisture period, and the theoretical moisture penetration depths of various materials differ significantly. In calculation of moisture transfer between the material and the indoor air, the effective moisture penetration depth (EMPD) model is usually used. However, the EMPDmodel is based on the assumption that the moisture does not penetrate through the material layers. The theoretical moisture penetration depth can be used to check the effectiveness of the EMPDmodel. The theoretical moisture penetration depth can also be used for material design reference.
Theoretical moisture penetration depth; Effective moisture penetration depth; Humidity control material
1671-6612(2017)03-240-05
TU86
A
国家自然科学基金(51178201);中央高校基本科研业务费专项资金(2015QN116)
万 航(1992-),男,博士研究生,E-mail:wanhang111@hotmail.com
徐新华(1972-),男,教授,E-mail:bexhxu@hust.edu.cn
2016-04-13

