基于用户部分特征的协同过滤算法①

2017-10-13 14:47李永超

计算机系统应用 2017年3期

李永超, 罗军

基于用户部分特征的协同过滤算法①

李永超, 罗军

(国防科技大学计算机学院, 长沙 410073)

协同过滤算法作为推荐系统中应用最广泛的算法之一, 在大数据环境下面临严重的数据稀疏问题, 使得近邻选择的效果不佳, 直接影响了算法的推荐性能. 为了解决这一问题, 本文提出了一种基于用户部分特征的协同过滤算法(UPCF), 该算法首先基于评分偏差和项目流行度进行矩阵缺失值填充, 随后利用初始聚类中心优化的K-means算法对该填充矩阵进行项目聚类, 并利用用户在项目分类下的局部特征进行近邻集合构建, 最终采用基于用户的协同过滤算法获得推荐. 我们采用流行的MAE指标对算法在MovieLens数据集上进行评测. 实验表明, 与目前流行的协同过滤算法相比, 提出的UPCF算法在没有增加算法复杂性的前提下, 性能有近10%的提升.

项目流行度; 最近邻选择; 项目聚类; 协同过滤算法

1 引言

随着互联网的兴起, 互联网上的信息呈指数化增长, 人类进入了信息爆炸的大数据时代. 如何从浩瀚的数据信息中获取自己感兴趣的信息, 已成为人类面临的巨大难题. 于是无需用户提供明确需求, 仅通过用户历史行为主动帮助用户快速有效筛选信息的推荐系统应运而生[1]. 我们在互联网网站中看到的“猜你喜欢”, “大家都在看”, “看过的也看”, “你可能会感兴趣”等都是推荐技术的实际应用. 据报道, 早在2002 年, 在线购物企业Amazon 总销售额的20%便源自它的推荐系统. 推荐技术在新闻领域更是产生了“今日头条”这样的不生产内容, 仅依靠推荐引擎便拥有3.5 亿注册用户, 3500 万活跃用户的新兴科技媒体.

协同过滤作为推荐系统的主流技术之一, 主要包括基于用户的协同过滤推荐、基于项目的协同过滤推荐和基于矩阵分解的协同过滤推荐[2]. 而其中基于用户的协同过滤算法是目前在实际应用中最为成功的算法. 该算法首先通过用户间的共同评分项计算用户间的相似度, 然后根据用户间的相似度选择目标用户的近邻集合, 最后根据用户近邻集合对目标用户进行推荐. 最近邻选择作为该算法中最关键的步骤, 直接决定了推荐的质量. 然而在实际应用中由于数据集中项目的维度巨大, 大多数用户只会对极少数的项目进行评价, 从而导致用户评分数据的极端稀疏,不同用户间的共同评分项极少,用户间相似性计算的可靠性和准确性难以得到保证, 推荐算法的效果大打折扣.

为了解决稀疏性问题, 多种措施相继被提出. Ungar LH等[3]首次提出基于用户聚类的协同过滤算法(UBCF), 通过用户聚类来降低最近邻搜索的数据规模, 增加最近邻可靠性. 黄裕洋等[4]根据评分数据的稀疏性情况, 提出了一种动态计算相似性的方法(HCFR). Xavier Amatriain[5]等提出在提前构建的专家集合中寻找用户近邻集合, 以确保用户的近邻对待预测项目有过评分记录. 黄创光等[6]提出了一种不确定近邻的协同过滤推荐算法(UNCF). 该算法通过不确定近邻因子及调和参数去计算基于用户和产品的预测评分并产生推荐. Koren Y[7]通过将矩阵分解和最近邻算法相结合, 大大提高了算法的推荐性能.

以上方法虽然从一定程度上减弱了数据稀疏对近邻选择带来的影响, 提高了协同过滤的推荐质量和效率, 但在最近邻计算的过程中, 对用户的相似性计算仍基于全局相似性, 没有充分考虑用户在不同项目类别下的兴趣差异. 正如世上没有完全相同的两片树叶一样, 在各个方面兴趣都相似的用户也难以寻找. 大多用户可能只在某个领域内兴趣相仿, 在其他领域内可能兴趣完全相悖. 因此本文提出了一种基于用户部分特征的协同过滤算法UPCF, 该算法首先对填充矩阵进行项目聚类, 然后仅根据用户在该项目分类下的所有评价进行相似度矩阵构建, 降低数据维度的同时提升了最近邻计算的可靠性, 最后根据相似性矩阵进行近邻集合构建, 从而最终得到推荐结果.

2 问题定义及基本方法

基于用户的协同过滤算法基于以下假设: 如果用户之间对一些项目的评分比较相似, 则他们对其它项目的评分也将会比较相似. 协同过滤推荐系统首先搜索目标用户的若干近邻, 然后根据最近邻对项目的评分去预测目标用户对项目的评分, 从而产生推荐列表. 作为算法的输入, 数据源=(,,), 其中={u,u,···,u}是基本用户的集合,;{i,i,···,i}是项目集合,.阶矩阵是用户对各项目的评分矩阵, 其中的元素r表示中第个用户对中第个项目的评分. 基于用户的协同过滤算法主要包括以下三个步骤.

2.1 评分矩阵预处理

由于在实际应用中, 项目集的维数很大, 用户只能对极少数项目进行评价, 因此评分矩阵十分稀疏, 这对后面的相似性计算提出了很大的挑战. 合理的矩阵缺失值预测填充可以从一定程度上缓解稀疏性问题.

目前常用的缺失值预测方法包括评分中值、众数、用户评分均值、项目评分均值、采用奇异值分解填补近邻评分缺失值[7]以及基于近似项目预测评分值[8]等.

2.2 用户近邻集合构建

接下来, 我们在预处理过的用户评分矩阵上采用相似度计算方法, 计算用户之间的相似度, 形成用户的相似度矩阵. 协同过滤算法研究中最常用的相似度计算方法是相关相似度、余弦相似度和修正的余弦相似度, 它们的计算公式分别如下:

3 基于用户部分特征的协同过滤算法(UPCF)

传统的基于用户的协同过滤算法在计算最近邻的过程中使用了用户的所有评分记录, 考察了用户的全局相似性. 然而在全部项目集上兴趣都相似的用户并不常见, 大多用户可能只在某一主题下兴趣相似, 而在其余项目分类中喜好完全不同. 因此传统的近邻集合构建往往选择了全局相对相似而舍弃了在某些领域内兴趣高度契合的用户. 为了解决这个问题, 本文提出了一种基于用户部分特征的协同过滤算法, 使得在最近邻选择时所需的相似度仅根据用户在该项目所在类内的评价信息计算获得. 算法详细流程如下所示.

3.1 未评分项目预测填充

为了缓解在项目聚类时矩阵的稀疏问题, 我们首先对评分矩阵进行缺失值预测填充. 考虑到热门项目对用户特征贡献度不大, 以及相对冷门项目而言, 用户接触到热门项目的概率大得多, 而如果用户未对热门项目进行反馈评价, 很可能是因为用户对该项目并不感兴趣. 而在推荐系统中, 项目流行度是衡量项目热门程度的主要指标, 它是指项目被用户反馈的总次数, 被反馈的次数越多代表项目流行度越高. 因此为了能够从一定程度上合理惩罚未评分热门项目, 我们引入了项目流行度权重系数,在此次试验中, 我们采用以下公式计算项目流行度, 其中()表示项目已被评分的总次数.

项目被评分总次数()越大则对应权重越小, 预测评分则会相应降低.最终我们采用如下方法进行缺失值预测填充.

3.2 项目聚类

缺失数据处理过后, 我们便可对项目进行聚类, 本次我们采用聚类算法中最经典的K-means算法进行项目聚类. 而传统的K-means算法对初始聚类中心非常敏感, 聚类结果随不同的初始输入而有较大波动. 为消除这种敏感性, 本文采用袁方等提出的优化初始聚类中心的改进K-means算法[9]进行聚类计算. 与传统聚类算法不同的是, 该算法在选取初始聚类中心时计算每个数据对象所在区域的密度, 选择相互距离最远的个处于高密度区域的点作为初始聚类中心. 实验表明改进后的K-means算法能产生质量较高的聚类结果, 并且消除了对初始输入的敏感性.

过程1. 基于项目的kmeans聚类输入: 聚类数目k, 最大迭代次数iter_num和用户评分数据填充矩阵R输出: k个聚类 1) 计算以项目集I中每个项目ij为中心, 包含常数Minpts个数据对象的半径, 记为ij的密度参数. 越大, 说明数据对象所处区域的数据密度越低. 反之则说明数据对象所处区域的数据密度越高. 选取满足的点ij为高密度区域D. 取D中处于最高密度区域的点作为第1个聚类中心rl; 取D中距离rl最远的点作第2个聚类中心r2; 计算D中各数据对象ij到rl, r2的距离d(ij, r1), d(ij, r2), r3为满足max(min(d(ij, r1), d(ij, r2)),j=1,2···n的数据对象ij; rm为满足max(min(d(ij, r1), d(ij, r2)...d(ij, rm-1)),j=1,2···n的数据对象ij,ij∈D. 依此得到k个初始聚类中心. 记为集合centerold={r1, ···, rk}; 2) k个聚类簇cluster1, ···clusterk均初始化为空, 记为集合Cluster=(cluster1, ···clusterk)3) REPEATFOR each item i in I:FOR each center rjin centerold : 计算项目i和聚类中心rj的相似性; sim(i,rm)=max(sim(i,r1),sim(i,r2),···,sim(i,rk))EndforFor each clusterm in Cluster: 计算clusterm的均值, 生成新的聚类中心cnewm. Centernew={cnew1,cnew2,···, cnewk}EndforUTILCenterold=(c1, ···ck)和Centernew=(c1, ···ck)相同或达到最大迭代次数iter_num.4) 返回Cluster.

3.3 推荐生成

为了保证预测的精确性, 避免提前引入误差, 我们在评分预测阶段采用原始用户评价矩阵而非填充矩阵. 并使用公式(1)计算待推荐用户在待推荐项目所在类内与其余用户的相似度, 构建用户相似性矩阵. 查找与用户相似度最大的个最近邻. 使用公式(4)计算用户预测评分, 得到最终评分预测值, 算法过程如下.

过程2. 评分预测输入: 原始用户评价矩阵R, 最近邻个数n, 待预测评分用户u, 项目i, 项目i所在聚类簇clusterj=[il,ij,···,ip]. 输出: 评分预测值 1) simDict={}2) For user v in U: IF v!=u: simDict[v]=sim(u,v) Endif Endfor3) Nu=sort(simDict)[:n]4)

其中, 此处,的特征向量为=(,,···,),= (,, ··· ,). sim(,)我们采用公式(1)所提供的相关相似性计算. 算法的复杂度为. 至此, 我们便可获得指定用户对指定项目的评分预测值, 为随后的推荐提供支持.

4 实验结果及分析

本次实验的硬件平台是配置Intel pentium E58003.2 GHz CPU, 4G RAM, 操作系统为ubuntu 14.04的个人计算机, 所有程序均由python实现.

4.1 数据集

本文采用的实验数据集是目前衡量推荐算法质量常用的著名电影评分数据集MovieLens中的100k数据集(http://grouplens.org/datasets/movielens), 该数据集由美国明尼苏达大学GroupLens研究小组创建并维护. 该实验数据集共包含930个用户对1682部电影的100000条评价信息, 其中每个用户至少对20部电影进行了评分, 每个电影也都收到了用户评论. 该数据集的稀疏性为1-100000/(943*1682) = 0.937. 数据集中用户评分范围是1-5, 数值越大代表用户对该电影的兴趣越大. 本次实验按照80%和20%的比例随机的将数据集划分成为训练集和测试集, 随后进行5-折交叉实验, 取五次试验的平均值作为最终结果.

4.2 评价标准

平均绝对误差MAE(mean absolute error)是目前学术研究中应用广泛的推荐系统推荐质量评价标准. 其主要通过公式(7)计算测试集中用户实际评分和推荐算法根据训练集的训练预测值的差的绝对值均值, 平均绝对误差MAE越小, 推荐算法的质量越高. 其中表示测试集的数据个数,p为预测评分值,r为测试集中的实际评分值.

4.3 实验结果分析

我们首先研究聚类个数对本文算法性能的影响. 实验结果如图1所示, 其中横坐标表示聚类个数, 纵坐标表示MAE值, 最近邻个数统一取=30.

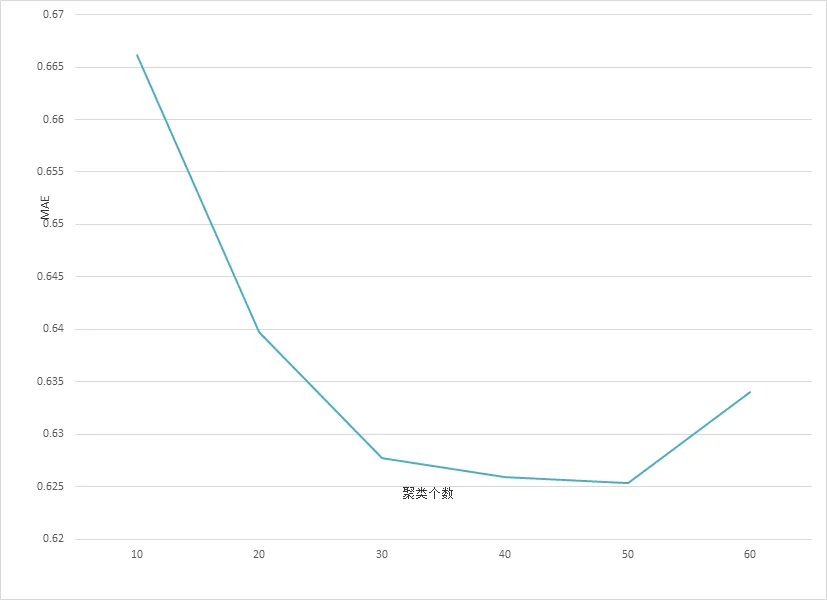
图1 聚类个数对MAE值的影响

通过图1我们可以清晰看到刚开始, 随着聚类族数的增多, 算法性能不断提升, 当项目聚类个数为50时, 算法取得了最好的性能, 此后聚类族数的增多反而引起算法性能的下降. 接下来, 我们通过将本文所提出算法UPCF与传统的基于用户聚类的协同过滤算法(UBCF)[3]、综合用户和项目因素的协同过滤推荐算法(HCFR)[4]、基与不确定近邻的协同过滤算法(UNCF)[6]的平均绝对误差MAE进行对比观测试验性能. 为了缩短算法的运行时间, 聚类个数均设置为20.

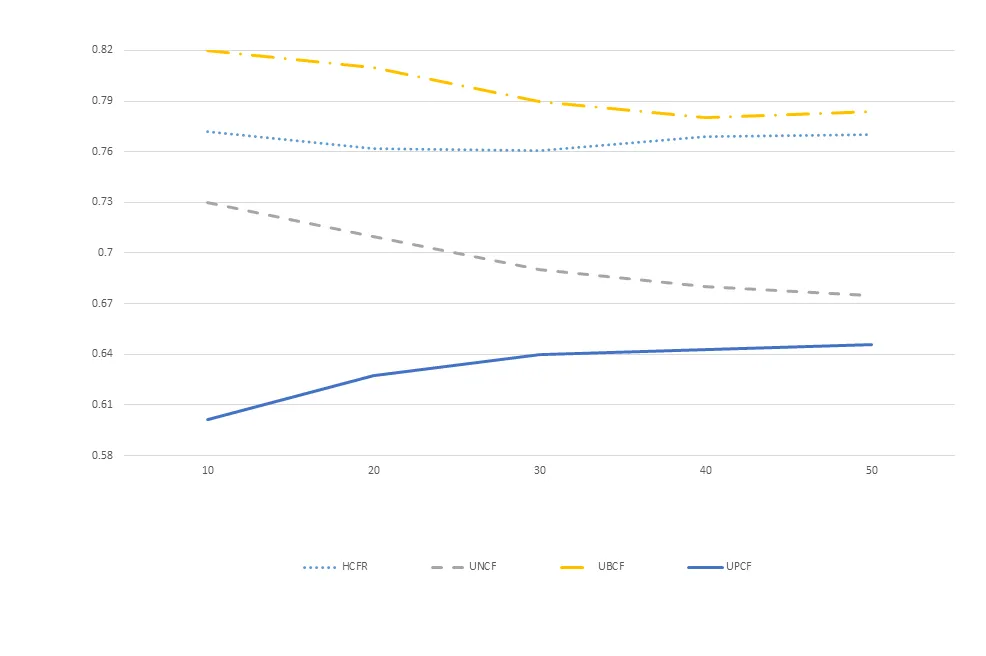
图2 算法性能比较

由图2可以看出, 本文算法与其他算法在MAE值上有了10%左右的提高, 特别是当近邻个数比较少的时候, 本文算法体现了非常好的推荐效果, 性能优势明显更好, 这充分说明本文提出算法最近邻选择的高效合理性. 我们也可以观察到, 当最近邻个数达到一定数量后, 所有算法的MAE性能趋于平稳, 这也反映出当近邻相似度不断减小时, 该近邻对算法的性能提升没有显著的影响.

此外, 本文算法在提高推荐质量的同时并没有带来算法复杂性的提升. 数据的预填充和项目聚类均可提前离线完成, 仅需根据需求隔一段时间更新. 而评分预测由于不再依赖用户全局特征, 单个评分预测的复杂性由变为, 其中表示用户总个数,表示项目总个数,表示项目聚类个数. 用户还可根据实际需求, 并行的在各个项目类内进行用户评分预测.

5 总结

针对传统协同过滤算法中最近邻计算时所面临的稀疏性和准确性挑战, 本文提出了一种基于用户部分特征的协同过滤算法. 该算法采用基于评分偏差与项目流行度的思想进行缺失值填充, 并在最近邻构建时仅考虑用户在该项目分类下的特征, 动态的根据待预测项目筛选用户最近邻, 从而提高了推荐的质量. 此外, 由于仅需考虑用户类内特征, 该算法实现了一定程度的降维, 降低了算法的复杂性. 并可根据需要, 分布并发的计算各个类内用户的预测评分值, 一定程度上提高了算法的实时性.

但算法中项目分类以及用户最近邻选择时特征选择的准确性仍需要进一步研究改良, 所使用的聚类算法K-means的聚类效果仍不是十分理想. 此外, 在此次研究前期对推荐算法的了解中, 我们发现目前针对各种推荐算法模型的融合以及算法并行化的研究也成为业界的新热点. 而能够更好地反应用户兴趣的用户社交关系的引入[10,11]大大提高了协同过滤算法的近邻可靠性和准确性, 为算法的改良提供了新的方向. 如何将用户社交关系引入本文提出的算法, 进一步改善本文算法的性能, 将是下一阶段研究的重点.

1 Park DH, Kim HK, Choi IY, Kim JK. A literature review and classification of recommender systems research. Expert Systems with Applications, 2012, 39(11): 10059–10072.

2 Bobadilla J, Ortega F, Hernando A, Gutiérrez A. Recommender system survey. Knowledge-Based Systems. 2013, 46: 109–132.

3 Ungar LH, Foster DP. Clustering methods for collaborative filtering. AAAI Workshop on Recommendation Systems, 1998, 1: 114–129.

4黄裕洋,金远平.一种综合用户和项目因素的协同过滤推荐算法.东南大学学报(自然科学版),2010,40(5):917–921.

5 Amatriain X, Lathia N, Pujol JM, Kwak H, Oliver N. The wisdom of the few: A collaborative filtering approach based on expert opinions from the web. Proc. of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM. 2009. 532–539.

6 黄创光,印鉴,汪静,刘玉葆,王甲海.不确定近邻的协同过滤推荐算法.计算机学报,2010,33(8):1369–1377.

7 Koren Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. Proc. of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2008. 426–434.

8 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法.软件学报,2003,14(9):1621–1628.

9袁方,周志勇,宋鑫.初始聚类中心优化的K-means算法.计算机工程,2007,33(3):65–66.

10 Daly EM, Geyer W. Effective event discovery: Using cation and social information for scoping event recommendations. Proc. of the 5th ACM Conference on Recommender Systems. ACM. 2011. 277–280.

11 Guy I. Social recommender systems. Recommender Systems Handbook. Springer US, 2015: 511–543.

Collaborative Filtering Algorithm Based on User Partial Feature

LI Yong-Chao, LUO Jun

(Department of Computer Science, National University of Defense Technology, Changsha 410073, China)

As one of the most widely used algorithms in recommender system, the traditional collaborative filtering algorithm faces serious data sparseness problem in the big data trend, which leads to the ineffective in nearest neighbor selection, and restricts the performance of the algorithm. To address this problem, this paper proposes a collaborative filtering algorithm based on user partial feature(UPCF). In our method, it first rates the missing values based on rating bias and item popularity; and then clusters the items in the filled matrix with a K-means clustering algorithm of meliorated initial center. At last, it uses the user-based collaborative filtering algorithm with the user feature in item class to get the recommendations. The MAE measures on the MovieLens dataset shows that compared with the current popular algorithms, the performance of our UPCF algorithm improves about 10% without any increase of algorithm complexity.

item popularity; nearest neighbor selection; item clustering; collaborative filtering algorithm

2016-07-01;

2016-08-31

[10.15888/j.cnki.csa.005704]