让学生经历建模过程 提高概念教学的有效性——以“方程的意义”为例

⌾梁志芹

让学生经历建模过程提高概念教学的有效性
——以“方程的意义”为例

⌾梁志芹

小学概念教学是数学教学中一项重要的内容，是整个小学知识体系的基石，是学生学习数学知识的起点和保证。数学概念往往是抽象的， 而小学生是以直观、形象思维为主，抽象思维能力还比较低，对概念的理解有一定的难度。本文试着以“方程的意义”为案例，从小学生概念形成及获得的一般过程“感知概念——抽象概念——应用概念”来谈一谈怎样进行小学数学概念的建构，提高概念教学的有效性。

概念；表象；抽象；构建；应用

概念是思维过程的核心，在布鲁纳看来，帮助学生有效地习得概念，是学校教育的基本目的之一。小学概念教学是数学教学中一项重要的内容，是整个小学知识体系的基石，是学生学习数学知识的起点和保证。数学概念的一个显著特征就是“抽像性”，而小学生是以直觉思维为主，抽象思维尚未完全发展，概括能力还比较弱，对概念的理解有一定的难度。在课堂教学中，教师要重视概念的教学，让学生经历概念的建模过程，通过观察、实验、猜测、计算、验证等活动过程，让学生形成并获得概念。

一、感知概念，形成表象

《新课标》指出“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上”。根据皮亚杰的儿童认知发展阶段论，小学生的思维正处于从直观形象思维逐步向概括抽象思维的发展时期，他们基本上还是依赖于生活经验和感性认识。因此，在数学概念的学习中，教师应充分考虑到学生的认知规律及兴趣、需要和能力，创设情境，向学生提供丰富感性材料，在头脑中建立起有关概念的感知及表象。为了让学生充分的感知“方程”的概念，我设计了两个活动。

活动一：跷跷板。创设情境：动物园里的小动物玩跷跷板，跷跷板一边坐着一只小猪，小免、小猴、小狗分别跳到另一边。运用直观形象的呈现方式，以有趣的动漫形式，初步感知“平衡”，激发学生的学习兴趣。

活动二：用天平称物体。数学的许多概念都从现实生活中抽象出来的，所以我们要从现实生活中寻找素材创设数学情境。

情境一：认识等式。天平左边放一个300克和一个150克的橙子，天平的右边放一个450克的菠萝(300+150=450)

情境三：认识含有未知数的式子。

图1：天平左盘放一个玻璃杯，右盘放一个100 g重的砝码。

图2：往空杯中倒满水，右边加1个100g砝码。

图3：在天平右边加不同的砝码，根据天平不同的状况得到不同的式子。

学生的直接经验是数学学习得以进行的根基和源泉，是学生学习活动的起点和基础。学生对天平的平衡性质在科学课里已经了解了，通过直观的情境，让学生观察天平从不平衡到平衡的变化过程，把学生原有的经验和知识与概念整合，体会方程的性质，帮助学生形成对概念的表象，使概念具体化。

二、抽象建模，形成概念

概念学习实质上就是对一类对象关于数量关系与空间形式的本质属性进行抽象概括的过程，需要让学生亲身经历数学的发现、发生、发展的过程，通过这个过程，抽象出模型，形成概念。

1.动手操作，抽象概念 教学中，对于一些相对抽象的内容，要尽可能地利用恰当的演示或操作使其转化为具体内容，然后在此基础上抽象出概念的本质属性。因此，在教学“方程的意义”时，我设计了以下的教学过程。

（2）在高考数学命题中聚焦数学学科核心素养的考查既符合数学课程改革的方向，也有利于引导高中数学教学回归到正确的育人轨道上来．随着以大数据、人工智能技术为代表的一系列现代科学技术的兴起，数据分析早已经深入到科学、技术、工程等各个领域．为适应未来的工作与生活，高中学生必须具备一定的数据分析、数学建模素养．建议在高考命题中适当调整数学运算素养考查权重，加强对数据分析、数学建模素养的考查，设置更为真实的情境，把对数学核心素养的考查融入到具体的学科知识内容和思想方法当中．

⑴小组活动。

①先自己想一想，再小组讨论按什么标准分类。

②把信封里写有式子的纸条倒出来放到硬纸板上分一分。(天平情境中的各种式子)

⑵展示交流。

⑶第二次分类。

⑷抽象概念。像这样含有未知数的等式，称为方程。

教学中，教师应该给学生提供充足的从事数学活动时间和空间，让学生在动手实践、自主探索和合作交流的氛围中经历观察、实验、猜测、推理验证等活动过程，解除困惑。在这个活动中，通过学生想一想、说一说、分一分、议一议体会方程的本质特征，在操作实践活动经历方程的建构过程，从而抽象出模型，形成概念。

2.分析交流，理解概念 对于定义式的数学概念，教师要抓住概念关键词，明确概念的本质属性；要通过不同的呈现形式，了解概念的内涵和外延；要注重联系和区别，化抽象为形象，使学生全面的理解概念。

活动一：先让学生说一说“要判断一个式子是不是方程必须具备哪些条件”，再写几道方程。

活动二：猜一猜。下面的式子是方程吗？

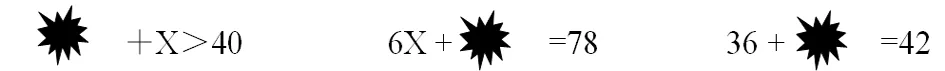
活动三：等式和方程的关系。

想一想，等式与方程有什么关系？你能画一个图来描述等式和方程的关系吗？

数学的抽象是逐级上升的。“活动一”学生在全面了解概念的含义基础上化抽象为具体，“活动二”让学生通过猜测验证来进一步理解概念，而“活动三”则让数与形相合，使概念系统化。

三、实践应用，获得概念

数学概念的学习不能依靠简单的模仿和记忆，小学生对概念的掌握需要由具体到抽象、再由抽象到具体多次往复，需要学生通过运用概念进行判断、推理、应用，在多次的实际应用中再认识，从而加深对数学概念的理解。

为了让学生更好的理解“方程的意义”，我设计了不同层次的练习，通过不同的呈现形式，让学生进一步理解概念，从而获得概念。

⑴把下面式子中的方程找出来。

①3+ X②50÷2=25③a+b=12 ……

⑵游戏。抽部分同学，每人手拿一张写有各种式子的卡片，安教师的要求，做“蹲、举、走、围”等动作，最终形成“式、等式、方程”的关系集合图。

⑶根据情境图列方程。

⑷根据信息写方程。选取与学生息息相关的生活素材，如“衣、食、住、行、玩”等，根据生活情境写方程，让学生感受生活处处有数学，激发学生的学习兴趣。

《新课程标准2011年版》明确提出：义务教育阶段的数学课程，应遵循学生学习数学的心理规律，强调从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展。因此，在小学数学的概念教学过程中，教师要设计学生熟悉的生活情境，让学生充分经历数学概念的建模过程，提高概念教学的有效性。

[1]郑毓信. 多元表征理论与概念教学[J]. 小学数学教育，2011，10

[2]闫天灵. 小学数学概念教学策略的研究[D].天津师范大学，2010.

[3]《数学新课程标准(2011年版) 》

[4]《新版课程标准解析与教学指导》

广东省云浮市新兴县实验小学 527400)