减振器阀系不等外径多阀片结构变形分析
杨成龙, 彭建设, 孙付春, 王培松
(1.成都大学 机械工程学院, 四川 成都 610106; 2.四川宁江山川机械有限责任公司, 四川 成都 610106;3.四川工业科技学院 交通学院, 四川 德阳 618500)
减振器阀系不等外径多阀片结构变形分析
杨成龙1,2, 彭建设1, 孙付春1, 王培松3
(1.成都大学 机械工程学院, 四川 成都 610106; 2.四川宁江山川机械有限责任公司, 四川 成都 610106;3.四川工业科技学院 交通学院, 四川 德阳 618500)
通过环形弹性复原阀系的力学模型,对减振器复原阀和压缩阀的不等外径多阀片结构弯曲变形进行了分析.利用单环形薄板变形理论推导,单阀片边界条件为内圆固定约束、外圆自由,求得了单阀片变形弯曲系数,给出了任意位置阀片变形的解析计算公式.对不等外径多阀片进行有效变换并利用单阀片叠加原理求得了不等外径多阀片结构变形解析理论公式.最终将解析计算与ANSYS仿真结果进行对比,相互验证了边界条件的处理和等效变换及理论解析计算的正确性.
减振器;复原阀;变形系数;叠加原理;等效变换;ANSYS仿真
0 引 言
筒式液压减振器是轮轨车辆广泛采用的一类减振器装置,其阻尼力通过油液流经孔隙的节流作用产生,其对于车辆的平顺性和行驶安全性有重要影响[1-4],由于减振器阀系内部的工作过程不方便测量和观察,而阀系阀片在一定压力的弯曲变形量对减振器阻尼特性起着关键作用,对减振器的设计和计算非常重要[5].对此,科研人员对减振器阀系阀片进行了深入研究,提出了阀系阀片弯曲变形和弯曲变形系数等概念[6-10],以及多阀片叠加原理和不等外径阀片叠加等效变换原理[11-13].本研究利用弹性力学理论建立相应的方程通过解析求解的方法快速得到阀体内部结构变化情况和叠加阀片各处的弯曲变形量,拟为减振器设计提供相关的计算依据与方法.
1 减振器复原阀结构与变形分析
1.1 某车型减振器复原阀结构
作为研究对象的某车型减振器内部复原阀结构如图1所示.通过对该复原阀结构分析可知,复原阀具有等外径和不等外径圆环形薄板叠加,在流体作用下,由于压力的变化造成阀片开度的变化,进而控制流体流动并产生阻尼.从图1可以看出,垫片5在螺母6的作用下几乎不变形,由此,阀片1、2、3、4的边界条件为在垫圈5的外圆处固定约束,阀片外圆处自由.
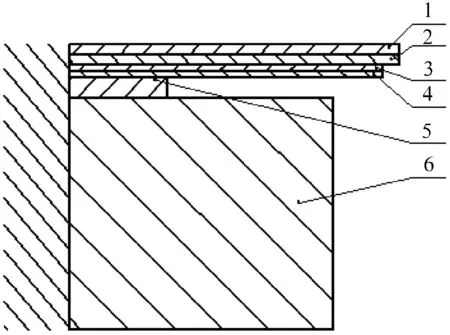
图1减振器复原阀结构示意图
1.2 复原阀变形分析
1.2.1 复原阀圆环形阀片变形分析.
该复原阀的圆环形阀片绕Z轴对称,由弹性力学理论可知,阀片变形曲面的微分方程为,
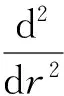
(1)
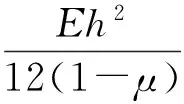
该微分方程(1)的通解为,
w=C1lnr+C2r2lnr+C3r2+C4+w*
(2)
其中,C1lnr+C2r2lnr+C3r2+C4为齐次方程的通解,w*为其特解.
假设q为作用在阀片上的均布压力,则D和q与半径无关,微分方程的特解为,
w*=Br4,
代入微分方程中得,
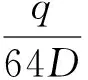
即,微分方程(1)的通解为,
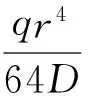
(3)
由边界条件可知:ra处固定约束,有ra处挠度,w(ra)=0,ra处转角,w'(ra)=0;rb处为自由端,剪力为0,rb处弯矩,即,
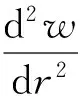

则,

(4)
求得待定系数为,
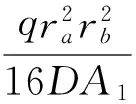

其中,


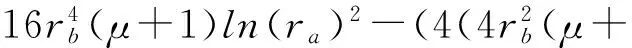

将通解待定系数C1、C2、C3、C4代入通解表达式中可求得弯曲变形表达式.

取,ra=5.5 mm,rb=9 mm,E=201 000 MPa,泊松比μ=0.3.G随r的关系为,
G=(K1ln(r)+(K2r2)ln(r)+K3r2+K4+K5r4)
(5)
其中,C1=K1q/h3;C2=K2q/h3;C3=K3q/h3;C4=K4q/h3;B=K5q/h3.
1.2.2 等效厚度叠加原理.
从式(5)可以看出,除了系数G外,阀片变形与阀片厚度和所受载荷有关,当N片阀片叠加时,总载荷为q=q1+q2+…+qn,有
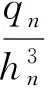

q=wh/G=w1h1/G+w2h2/G+…+wnhn/G
由于任意r处,变形w相等,由此得等效厚度h为,
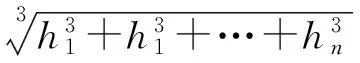
(6)
其中,n为阀片数.
1.2.3 外径等效原理.
根据等效厚度叠加计算原理,可以把不等外径而内径相等的多片叠加情况分割成多阀片等内外径叠加等效厚度进行处理(见图2).

图2多阀片叠加等效变换示意图
图2(b)中M是由图2(b)向上的力q2作用产生的弯矩.
阀系总体变形为,

(7)
1.2.4 支点处理原则.
在图1所示垫片5处的支撑作用下,垫片5的半径范围内,所有阀片变形非常小,相对复原阀片的变形,垫片的变形几乎可以忽略.据此可将变形内径外移,以rb5作为变形阀片的内径处理.
1.2.5 变形计算.
设阀片弹性模量201 000 MPa,泊松比0.3.由等效厚度原理,可计算出,
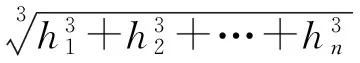

根据环形载荷等效处理,图3(a)可等效为图3(b).
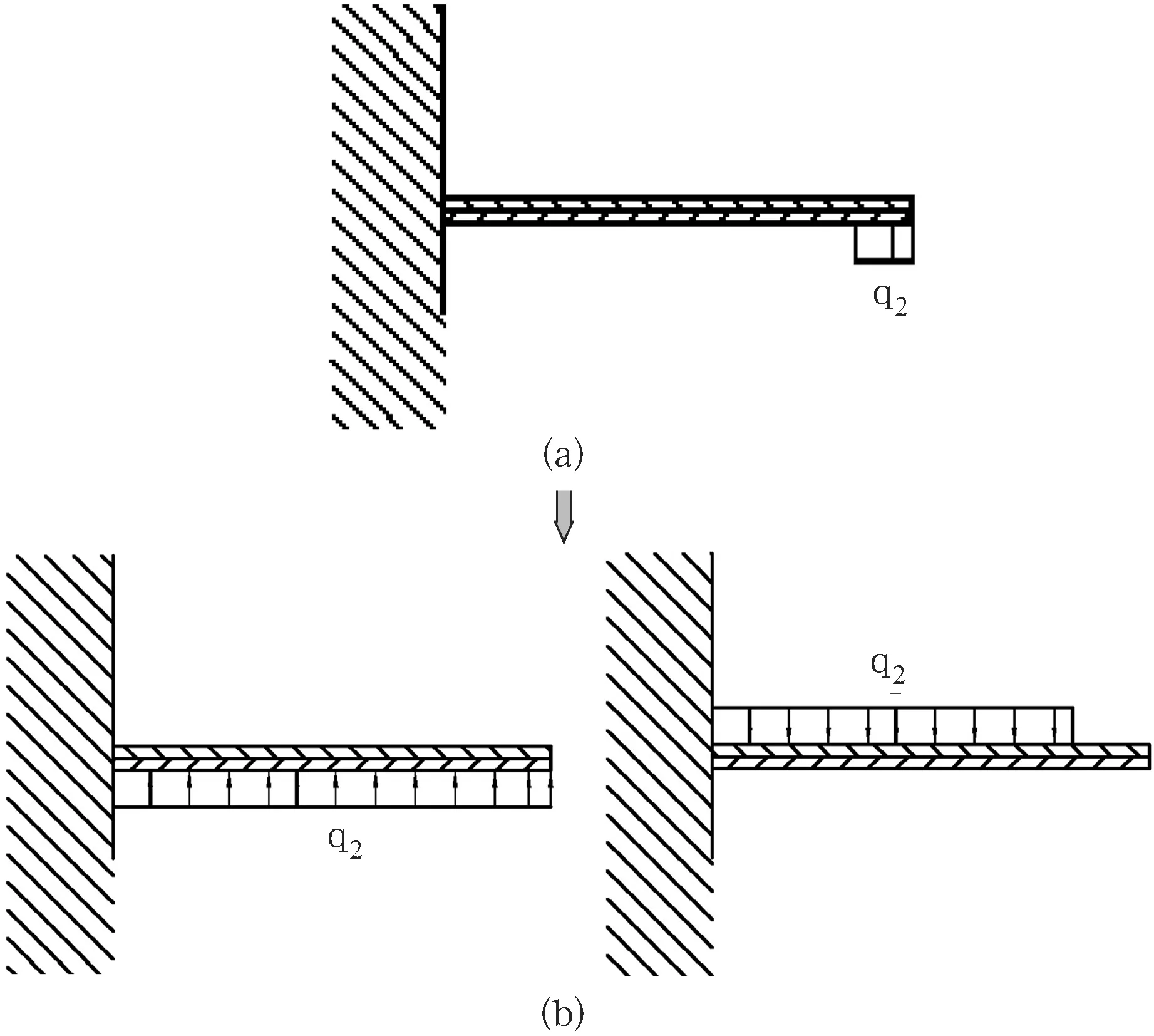
图3环形载荷等效原理
设阀片2下平面受压力0.1 MPa,根据式(7)可求出rb1.处阀片最大开度为w2=0.0233 mm.设阀片1下平面受压力0.1 MPa,根据式(7)可求出rb1处阀片最大开度为w3=-0.0217 mm.由此,图2叠加阀片最大开度处的变形为,
w=-0.0349+0.0233-0.0217
=-0.0333 mm.
2 仿真分析
2.1 对比计算
2.1.1 单阀片计算结果对比.
取内径为10 mm,外径为17.6 mm,厚度为0.2 mm的阀片,内圆环固定,外圆环自由,受载荷0.3 MPa.
对该实例,解析式计算得自由端(最大开度)w=-0.0589 mm;有限元计算采用ANSYS 17.0,网格密度为0.5 mm,仿真结果w为-0.0569 mm(见图4).据此可见,解析计算与仿真计算结果误差为3.4%.
2.1.2 多阀片叠加计算结果对比.
多阀片叠加结构如图3(a), 内圆环固定, 外圆环自由,上平面受载荷0.4 MPa,下平面受载荷0.1 MPa.

图4单阀片变形仿真计算结果
对该实例,解析式计算得自由端(最大开度)w=-0.0333 mm.有限元计算采用ANSYS 17.0,网格密度为0.1 mm,仿真结果为-0.033384 mm(见图5).解析计算与仿真计算结果误差为0.25%.
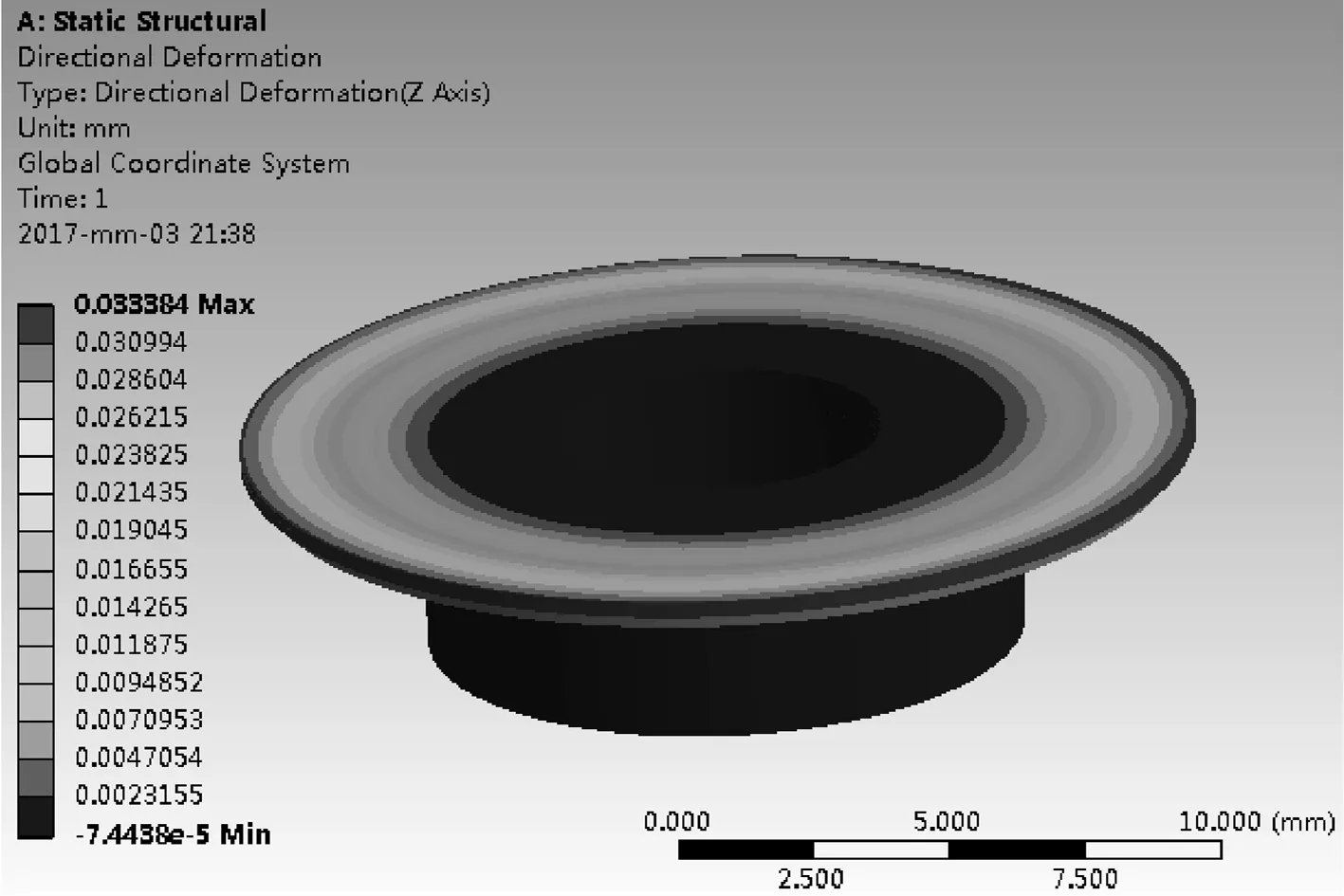
图5复原阀变形仿真计算结果
2.2 结 论
本研究的解析算法通过与有限元仿真对比计算可以看出,采用本研究提出的不等外径多阀片叠加方法求得的解析结果与有限元仿真结果误差比较小.可以认为,本理论计算过程可使用于如减振器这类产品的多阀片叠加结构的计算.
3 结 语
本研究利用弹性力学理论提出了圆环形阀片变形系数与阀片内径、外径、厚度和阀片材料的关系表达式,推导出了多阀片叠加等效原理,提出了内径固定端与环形载荷等效处理原理,并利用等效原理处理不等外径阀片叠加计算阀片最大开度问题.通过与有限元仿真结果对比,确定叠加原理和等效变换的计算可行.
[1]陈龙,汪若尘,江浩斌.基于大系统理论半主动悬架系统[J].机械工程学报,2008,44(8):97-101.
[2]李世民,吕振华.汽车简式液阻减振器技术的发展[J].汽车技术,2001,32(8):10-16.
[3]江浩斌,杨如泉,陈龙,等.麦弗逊式前悬架液力减振器阻尼特性仿真与试验[J].汽车工程,2007,29(11):970-974.
[4]赵亮,文桂林,韩旭,等.基于磁流变阻尼器的车辆半主动悬架最优控制的研究[J].汽车工程,2008,30(4):340-344.
[5]周长城,郑志蕴,徐伟,等.汽车减振器阀系参数建模及CAD软件开发[J].汽车工程,2009,31(3):262-266.
[6]杨成龙,孙付春,黄尔宇,等.农用车辆悬架减振器流固耦合分析[J].中国农机化学报,2017,61(2):57-62.
[7]江浩斌,杨如泉,陈龙,等.麦弗逊式前悬、架液力减振器阻尼特性仿真与试验[J].汽车工程,2007,29(11):970-974.
[8]吕振华,伍卓安,李世民.减振器节流阀非线性特性的有限元模拟分析[J].机械强度,2003,25(6):614-620.
[9]Yamaguchi T,Fujii Y,Takita A,et al.FEAfortransientresponsesofans-shapedforcetransducerwithaviscoelasticabsorberusinganolinearcomplexspring[J].World Acad Sci Engin Technol,2012,6(11):2401-2408.
[10]Shams M,Ebrahimi R,Raoufi A,et al.CFD-FEAanalysisofhydraulicshockabsorbervalvebvhavior[J].Int J Autom Technol,2007,8(5):615-622.
[11]周长城,顾亮,王丽.节流阀片弯曲变形与变形系数[J].北京理工大学学报,2006,26(7):581-584.
[12]王铃燕,丁渭平,刘丛志,等.减振器节流阀片组当量刚度的有限元分析方法[J].噪声与振动控制,2016,36(1):38-44.
[13]周长城,张绍阁,顾亮.环形弹性阀片弯曲变形曲面方程及其解[J].山东理工大学学报(自然科学版),2006,22(4):8-11.
Abstract:Based on the mechanical model of the ring resilient restoring valves,the bending deformation of the multi-valve plate with different diameters of the restoring valve and the compression valve of the shock obsorber is studied.Based on the single annular plate deformation theory,when the boundary conditions of the single valve plate are that the the inner circle is as the fixed constraint and the external circle is free,the bending deformation coefficients of single valve plate are obtained.An analytic formula for the arbitrary position valve plate deformation is developed.Based on the effective conversion of the multi-valve plate with different diameters and the utilization of the sigle valve superposition principle,the analytic formula of the structural deformation of the multi-valve with different diameters is obtained.Finally,the theoretical analytic calculation is compared with the ANSYS simulation results,which mutually verify the correctness of the boundary conditions and the equivalent conversion and the theoretical analytic calculation.
Keywords:shock absorber;restoring valves;deformation coefficients;superposition principle;equivalent transformation;ANSYS simulation
AnalysisonStructuralDeformationofMulti-valvePlatewithDifferentOuterDiametersofShockAbsorberValve
YANGChenglong1,2,PENGJianshe1,SUNFuchun1,WANGPeisong3
(1.School of Mechanical Engineering, Chengdu University, Chengdu 610106, China;2.Sichuan Ningjiangshanchuan Machine Co., Ltd., Chengdu 610106, China;3.Sichuan Institute of Industrial Technology, Deyang 618500, China)
U279.3+24;U463.33+5.1
A
1004-5422(2017)03-0289-04
2017-06-25.
杨成龙(1987 — ), 男, 硕士, 工程师, 从事机械与机构设计研究.

