水面无人艇冗余路径点约减方法研究——基于最优路径代价估计

温乃峰，刘冠群，于海洋，张汝波

(大连民族大学 a.机电工程学院；b.智能感知与先进控制国家民委重点实验室，辽宁 大连 116605)

水面无人艇冗余路径点约减方法研究
——基于最优路径代价估计

温乃峰a,b，刘冠群a,b，于海洋a,b，张汝波a,b

(大连民族大学 a.机电工程学院；b.智能感知与先进控制国家民委重点实验室，辽宁 大连 116605)

针对复杂海洋环境下USV在线路径规划问题，提出一种顺序-随机两模式的冗余路径点约减方法。利用估计通过路径点的最优路径来制定其被约减的概率，并通过概率值的自适应变化考虑更多路径点的组合方案。采用顺序方法控制随机约减范围，快速发现潜在的优化路径。在约减过程中考虑海流等复杂海况对USV运动的影响，从而降低USV的碰撞概率。实验结果表明，本文方法可有效地简化并优化USV路径。

水面无人艇；路径简化；冗余路径点约减；海流信息处理；随机化方法

Abstract:To solve the online USV path planning problem in complex ocean environment, we propose a two-mode redundant waypoints pruning method containing the sequential and probabilistic pruning modes. Regarding the problems of the path simplification as well as path optimization, an estimation method of the optimal path passing through a waypoint is raised to calculate the pruned probabilities of waypoints. At the same time, the pruned probabilities are changed adaptively to consider more waypoints combinations of a path to find a potentially better path. To reduce the pruning time, the scale of the probabilistic pruning process is constrained by the sequential pruning process. The influence caused by the complex sea state, such as current, is considered during the pruning process to decrease the collision probability of USV. The experimental results show that our method is better than the traditional methods in simplifying and optimizing USV paths.

Keywords:unmanned surface vehicle(USV); path simplification; redundant waypoints pruning; current information processing; randomized method

海洋环境瞬息多变，水面无人艇( Unmanned Surface Vehicle, USV)必须具有在线路径规划能力。由于时间有限，通常采用启发式快速路径规划方法，造成路径上冗余路径点和拐点较多，路径较曲折[1]。为了提高路径的平顺度，减少路径上的拐点，以进一步提高路径的优化性并降低跟踪的难度，需要对局部路径进行后期简化处理，在线约减冗余路径点[2-3]。USV的运动能力和载荷能力有限[4]，此时冗余路径点的约减对提高任务执行的效率和成功率非常重要。在线时间有限，要求冗余路径点约减方法必须高效。在约减过程中需要综合考虑路径执行时间、能耗以及路径与海流、障碍物、涡流区的关系，以保证路径的优化性和USV运动的安全性。约减结果不应与原始路径差异过大，以免过多丢失原始路径的优点。

1 研究现状

基于最优化方法的冗余路径点约减过程复杂度高，收敛慢，不能满足复杂运动的约束条件，难以应用于在线路径规划。针对这个问题，有研究人员提出了增量式快速约减方法(Incrementally Fast Pruning，IFP)、顺序约减方法(Sequential Pruning，SP)[5]和捷径法(Shortcut)[6]等典型快速约减方法。

传统SP方法顺序执行约减过程，初始条件下，将原始路径点集{n1,n2,…,nN}按顺序排列，令约减结果Np=Φ，当前约减路径点下标j=1。循环执行如下过程：将nj移入路径点集合Sp，令i=j+2，若nj与ni间存在无碰撞路径，且该路径段满足USV运动约束条件，则继续当前约减循环，i=i+1；否则，令j=i-1并重新开始约减循环；顺序约减直至路径末端点。

Shortcut方法在全路径范围内随机选择路径点对，并尝试用点对间直线路径代替原路径。随机选取过程可以保持约减过程的随机性和多样性，有助于找到SP方法无法发现的潜在的更优结果。但Shortcut方法路径点对的选择过程完全随机，难以全面地考虑路径的可行性和易行性，因此一些学者采用启发式方法选择点对，从而在约减过程中降低路径代价，本文借用这种思想设计随机约减过程。

为了提高USV的安全性，需要考虑海流对USV运动造成的偏差。通常采用障碍物膨胀法、误差走廊法及几何化方法，通过扩大路径与障碍物的间隔来降低碰撞概率。在环境建模过程中，向外扩充障碍物边界，或为路径设定宽度值，宽度值根据USV运动特性和实时参数设定[7]。也有文献对规划环境进行几何化处理，并在无碰空间的中轴线上规划路径，以追求路径与障碍物间隔最大化的目标，其中典型的方法包括泰森多边形方法和回退法。

泰森多边形方法需要对障碍物进行几何化预处理，为障碍物顶点划分泰森多边形，然后在各泰森多边形顶点处寻找路径点。但对空间预处理需要已知的环境信息且构建泰森多边形的时空复杂度高[8]，不适合在线路径规划问题。回退法[9]的流程：寻找路径点ni与障碍物距离最近的点oi；沿nioi矢量方向移动ni，直到oi与其它障碍物更近。

2 运动偏差处理

约减过程中海流对USV的运动产生影响，由于在线规划时间有限，对运动偏差处理方法的效率要求较高。几何化方法要求对环境精确建模，使得它的计算较复杂，水下先验环境信息通常带有未知性和动态性，难以预先构建精确环境模型。而且几何化方法只是单纯的增加路径与障碍物的间隔，未考虑海流信息，可能会造成间隔不合理。不仅额外增加了路径长度，还可能使路径距海流流向上的障碍物更近，增加了碰撞概率。

本文由启发式快速扩展随机树方法规划初始路径，通过碰撞检测技术避免对环境的精确建模，采用误差走廊法增加路径与障碍物间距离。估计海流造成的运动偏差距离为σt·Vc·sinαy，其中，σt为USV控制的时间节拍，Vc为海流流速，αy为海流方向与路径方向或USV运动方向的夹角。这里，USV的运动方向主要指它的偏航方向。

利用线性二次型高斯运动规划方法[10]近似地估计USV在路径上无碰撞的概率下限值pc。假设USV的位置服从n元高斯分布，那么，USV在某一路径点qi处无碰概率可近似为：Γ (n/2,Cq2/2) ，Γ为标准伽玛分布函数，Cq是根据USV与障碍物间最近距离和由海流造成的USV位置偏差的标准差δq计算得出的USV可偏离路径且无碰的位置分布标准差。

定义路径质量如下：路径段π的质量Q(π)为USV跟踪π时的无碰概率，它等于USV在π上所有的nw个路径点处的pc值的乘积，nw=10，如式(1)。通过在路径规划和简化过程中保证结果路径段的质量大于某阈值，来考虑USV自身的运动偏差和海流造成的偏差。

(1)

3 基于最优路径代价估计的冗余路径点约减

为了快速地约减冗余路径点并进一步优化路径，本文结合SP方法和Shortcut法，提出基于估计最优路径代价的冗余路径点约减方法(Optimal Path Cost Estimation based Redundant Waypoints Pruning Method，CEP)。CEP方法参照Shortcut方法制定了一种启发式随机约减方式，为了在随机约减过程中考虑路径的代价和易行性问题，估计通过路径点的最优路径代价，并根据代价计算约减路径点的概率，同时根据中间路径结果的代价自适应改变各路径点被约减概率。规定只有当路径代价由于约减而降低时，约减才会发生，以此保证结果路径收敛于更优的结果。为了弥补Shortcut方法收敛慢的缺点，CEP方法基于SP方法的顺序约减过程来缩小随机约减规模，只在前次顺序约减的终点之后到路径末端点的范围内进行随机约减。

定义路径点间的代价距离(Cost Distance，CD)：

CD(qi,qj)=Dγ1·D(qi,qj)+Dγ2·Ya-Dγ3·Vc·cosαy+Dγ4·Vc·sinαy+Dγ5·Tt。

(2)

式中，权值Dγ1+Dγ2+Dγ3+Dγ4+Dγ5=1；Vc为海流速度；αy∈[0,π]为海流方向与路径方向夹角。Vc·cosαy为逆流能耗指示变量，当αy<π/2时，海流对USV运动具有推动作用；当π/2<αy≤π时，逆向海流增加USV能耗。Vc·sinαy反应海流造成的运动偏差，当αy=π/2时，横向海流造成的偏差最大。CD用于启发CEP算法生成顺流且偏差较小的路径。Ya为USV由qi到达qj的偏航角的绝对弧度值。Tt为涡流对USV的威胁，令Tt=cos[(π·Rt)/(2·Rmax)]，Rt表示qi和qj与其最近的涡流区中心的距离之和，Rmax为涡流区的威胁半径，Rt≤Rmax。

定义通过路径点(qi)的估计最优路径的代价:

Cp(qi)=pγ·cost(qi)+(1-pγ)·CD(qi,Goal) 。

(3)

式中，pγ为权值;Goal为路径终点;CD(qi,Goal)是qi与Goal间的估计最优路径的代价。cost(qi)为从路径起始点到达qi的所有路径段的CD之和。

本文根据Metropolis准则[11]定义路径点被约减的概率如式(4)，该准则来源于模拟退火算法，

pp=1-exp[-Cp(qi)/(kp·Tem)]。

(4)

式中，Tem类似模拟退火算法中的温度参数，它负责控制约减过程路径点间竞争的激烈程度，在开始阶段，令Tem为较小值，此时，路径点间竞争较小。将路径点的pp值归一化后，Cp值较高的路径点的pp值明显高于Cp值较低的路径点的pp值，此时，竞争的激烈程度较弱，Cp值较大的路径点更容易被约减，而Cp值较小的路径点竞争力较弱。CEP算法保证约减后的路径代价低于原始路径代价，随着路径代价值下降，提高Tem值，增加竞争激烈程度，所有路径点pp值下降，而Cp值较大的路径点的pp值降低得更快，此时，路径点间的pp值差距变小，Cp值较低的路径点竞争力增加，被约减的可能性增加。约减过程的多样性增加，更有助于寻找潜在的低代价路径。

式(4)中kp的作用是限定函数的值域，令kp=(PCmax-PCmin)/2，PCmax为路径估计最大代价，令其为原始路径代价值，PCmin为路径估计最低代价，令其为路径起始端点间的CD值。令Tem随着路径代价的降低而线性增加，定义Tem函数：

Tem=-Kt·(PC-PCmax)+Temmin。

(5)

式中，KT=(Tmax-Tmin)/(PCmax-PCmin)；Tmax=0.8，Tmin=0.2分别为温度的最大值和最小值；PC为实时路径的代价值，由式(2)计算可得。

本文提出的冗余路径点约减算法CEP将约减过程分为Shortcut约减模式和SP约减模式，流程如下：

(1) 生成[0,1]间随机数Rand，若Rand大于Shortcut约减阈值Pr，根据SP算法选择顺序约减的起止点，若SP约减模式未完成全路径的顺序约减，执行步骤(2)，否则算法结束；

(2) 找到上一轮SP约减的终点，将其作为Shortcut约减的起点，为该起点到达路径末端点间所有路径点qi计算通过它的路径的估计最优代价Cp(qi)和其被约减概率PP，并根据PP值，使用轮盘赌方法选取拟被约减的路径点，该路径点的前后路径点作为此次Shortcut约减的起止节点；

(3) 执行约减流程，SP模式和Shortcut模式的约减过程一致，首先检查约减起止点间直线路径代价是否小于起止点间原始路径代价，若是，则继续检测起止点间直线路径是否满足USV的运动约束条件且无碰撞，以及路径段质量是否大于阈值0.1，若满足条件，则用起止点间直线路径代替起止点间原始路径。

本文CEP算法的平均时间复杂度为O(n2)。

4 实验结果和分析

4.1 实验环境设置

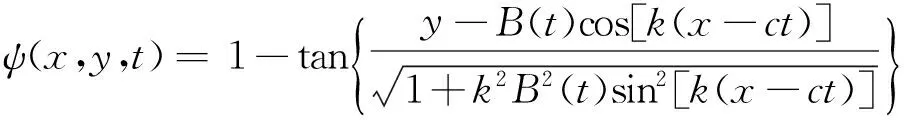
(6)

式中，B(t)=b+e·cos(ω·t+θ)，令b=1.2，c=0.12，k=0.84，ω=0.4，e=0.3，θ=π/2。海流的速度场是一个向量场，可以由ψ(x,y,t)得到：U(x,y,t)=∂ψ/∂y，V(x,y,t)= ∂ψ/∂x，U(x,y,t)和V(x,y,t)分别为t时刻海流沿X轴和Y轴方向的速度分量。

4.2 实验结果分析

CEP方法和传统顺序方法的约减结果如图1。阴影区为涡流区，随着区域远离涡流中心，涡流危险性降低，实体为障碍物。

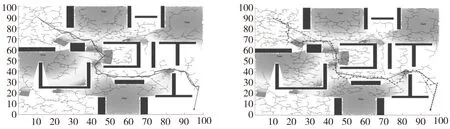
(a) CEP的一个约减结果 (b) CEP与SP的约减结果比较

图1(a)为CEP的一个约减结果，实线表示结果路径，虚线集CEP的中间结果，由于CEP在执行过程中考虑了路径优化和涡流区躲避问题，因此CEP逐步收敛于代价更优、危险性更低且更易行的路径，倾向于将路径向海流干扰较小、路径平顺度较高的方向调整。

图1(b)为CEP与SP方法的约减结果，原始路径用十字符号表示，而CEP与SP的结果路径分别用实线和虚线展示。CEP的结果路径距离原始路径较近，而SP方法偏离原始路径较大。这是因为SP方法持续约减路径点，直到新生成的直线路径不满足约束条件。CEP方法的结果路径能更多地保留原始路径的优点，安全性更高，而SP方法的结果路径存在距离涡流中心和障碍物较近的部分，且路径上存在较急的转弯部分，USV难以跟踪路径。本文CEP方法的拐点较少，路径较平顺，说明CEP方法在约减过程中考虑路径代价是有效的。

为了检验CEP方法的Shortcut约减模式的有效性，将CEP方法与它的SP约减模式的结果进行比较，而为了说明CEP的SP约减模式对提高算法收敛速度的有效性，将CEP方法与它的Shortcut约减模式的结果相比较，当单独执行Shortcut约减模式时，规定当路径代价的变化稳定且变化率小于10%时，算法结束。单独执行Shortcut约减模式时，算法执行时间超过CEP算法的10倍，代价降低率却只比CEP算法高了不到2%，这说明CEP方法比Shortcut约减方法更适用于约减时间有限的在线规划问题，CEP方法的SP约减模式具有有效性。CEP方法比单独使用SP约减模式多用了大约8%(0.2 s)的时间，但是其结果的代价降低率却比SP模式提高了5%，说明CEP方法中增加Shortcut约减模式的有效性。由于在约减过程中考虑了路径质量因素，因此，所有方法的结果路径均能保证碰撞概率在一定阈值范围内，且路径满足USV的运动约束条件。

在半实物仿真平台上规划出一次完整的路径，如图2。规划目标点成五角星形状分布在环境边缘。在线规划过程中集成了局部CEP方法，在每一控制时钟节拍，搜索出一条多步局部路径后，采用CEP方法对路径进行简化。

(a)海流强度较小时的路径约简结果 (b)海流强度较大时的路径约简结果

图2(a)所示为海流强度较小的时候的路径约简结果，从左上角的视图可以看出，结果路径比较平顺，拐点较少，路径能较直接地到达各个目标点，说明CEP方法能够有效地约减冗余路径点，并得到与目标点距离较近的路径，海流对约减过程影响相对较小。

图2(b)所示为海流强度较大的情况下的路径约简结果，约简算法在距离障碍物较远的外围寻路，说明海流对约简结果影响较大，这是因为海流因素在路径点代价计算过程中占据更大比重，算法更多地考虑了横向海流影响，以降低USV发生碰撞的概率，这同时表明算法在约简过程中海流因素发挥的作用，说明了约简过程中考虑海流因素的有效性，也表明本文约简算法的一种趋势，随着海流强度的增加，算法保留距离障碍物更远的路径。

5 结 论

本文针对USV在线路径规划过程中的路径简化问题，提出了一种最优路径代价估计方法和路径点被约减概率的计算方法，以及概率值的自适应变化方法，改进了传统的SP约减方法和Shortcut法。仿真结果表明，本文方法能够快速发现比传统方法更优的简化USV路径。在约减过程中考虑海流造成的运动偏差和涡流区威胁，降低了USV发生碰撞的概率。

[1] LAVALLE S M. Planning Algorithms[M]. Cambridge：University of Cambridge, 2006: 482-580.

[2] SEKHAVAT S, SVESTKA P, LAUMOND J P. Multilevel path planning for nonholonomic robots using semiholonomic subsystems[J]. The international journal of robotics research, 1998, 17(8): 840-857.

[3] CHEN P C, HWANG Y K. SANDROS: A dynamic graph search algorithm for motion planning[J]. IEEE Transactions on Robotics and Automation, 1998, 14(3): 390-403.

[4] ZHENG Z，SAMMUT K，LAMMAS A，et al. Efficient path re-planning for USVs operating in spatiotemporal currents[J]. Journal of Intelligent and Robotic Systems, 2015, 79(1): 135-153.

[5] NASIR J, ISLAM F, MALIK U, et al. RRT*-SMART: A rapid convergence implementation of RRT*[J]. International Journal of Advanced Robotic Systems, 2013, 10(4):299.

[6] GERAERTS R, OVERMARS M H. Creating high-quality paths for motion planning[J]. The International Journal of Robotics Research, 2007, 26(8): 845-863.

[7] CONNORS J, ELKAIM G. Analysis of a spline based, obstacle avoiding path planning algorithm[C]. 65th Vehicular Technology Conference, Dublin, Ireland, IEEE, 2007: 2565-2569.

[8] CHOSET H, BURDICK J. Sensor-based exploration: The hierarchical generalized voronoi graph[J]. The International Journal of Robotics Research, 2000, 19(2): 96-125.

[9] LIEN J M, THOMAS S L, AMATO N M. A general framework for sampling on the medial axis of the free space[C]. International Conference on Robotics and Automation, Taipei, Taiwan, IEEE, 2003, 3: 4439-4444.

[10] VAN B J, ABBEEL P, GOLDBERG K. LQG-MP: Optimized path planning for robots with motion uncertainty and imperfect state information[J]. The International Journal of Robotics Research, 2011, 30(7): 895 - 913.

[11] JAILLET L, CORTéS J, SIMON T. Sampling-based path planning on configuration-space costmaps[J]. IEEE Transactions on Robotics, 2010, 26(4): 635-646.

(责任编辑 赵环宇)

AnUSVRedundantWaypointsPruningMethodbasedonOptimalPathCostEstimation

WENNai-fenga,b,LIUGuan-quna,b,YUHai-yanga,b,ZHANGRu-boa,b

(a.School of Electormechanical engineering; b.Key Laboratory of Intelligent Perception and Advanced Control of State Ethnic Affairs Commission, Dalian Minzu University, Dalian Liaoning 116605, China)

TP311.5

A

2017-04-05；

2017-08-14

国家自然科学基金资助项目(61673084)；辽宁省自然科学基金项目(201602204)；中央高校自主科研业务费专项资金资助项目(DC201502010304)；辽宁省教育厅科学研究项目(L2014542)。

温乃峰(1981-)，男，辽宁葫芦岛人，讲师，博士，主要从事无人系统的路径规划技术、信息融合与人工智能研究。

2096-1383(2017)05-0461-05