高动态下GPS信号跟踪环路的仿真研究

王丽黎，孙文鹏

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

高动态下GPS信号跟踪环路的仿真研究

王丽黎，孙文鹏

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

GPS信号跟踪过程是GPS接收机的核心组成部分，它是将捕获阶段得到的各项参数进行精确估计的过程，实现本地生成信号与输入信号的准确同步。以高动态环境为前提，模拟生成GPS信号，改变卫星信号的加加速度，模拟高动态下所引起的多普勒频移，分别使用传统跟踪环路与扩展卡尔曼滤波环路对信号进行跟踪。仿真结果显示，扩展卡尔曼滤波跟踪环路更加稳定，精度有所提高。

高动态；GPS信号跟踪；卡尔曼滤波

Abstract: The GPS signal tracking process is the core component of the GPS receiver. It is the process of accurately estimating the parameters obtained in the capture phase. It realizes the accurate synchronization of the local generated signal and the input signal. Based on the premise of high dynamic environment, this paper simulates the generation of GPS signals, changes the acceleration of satellite signals, simulates the Doppler shift caused by high dynamic motion, and uses the traditional tracking loop and the extended Kalman filter loop tracking signal respectively. The simulation results show that the extended Kalman filter tracking loop is more stable and the accuracy is improved.

Key words:high dynamic; GPS signal tracking; extended Kalman filter

0 引言

全球定位系统(GPS)是基于人造卫星的面向全球的全天候、高精度的定位和定时系统，在军民领域均具有广阔的用途和发展前景[1-2]。跟踪模块作为GPS接收机的核心部分，直接影响接收机的动态性、精度等性能指标。捕获阶段是对当前卫星信号载波频率和码相位的粗略估计，跟踪环路则逐步精细对这两个信号参量的估计，同时输出对信号的各种GPS测量值，并且解调出信号中的导航电文数据比特。在高动态的环境下，会导致载波上附加大的多普勒频移，导致载波跟踪环容易失锁，跟踪将不能正常进行。若为了跟踪到信号而加大跟踪环路带宽，这样又使得跟踪环路中的噪声加强，影响跟踪精度。

卡尔曼滤波器是目前应用最广泛的状态估计方法之一，其最大的优点是采用递归的方法来解决线性滤波的问题[3]。本文在详细分析卡尔曼滤波的基本原理的基础上，将扩展卡尔曼滤波器应用于GPS信号的跟踪环路中，实现在高动态下跟踪环路的正常进行，确保跟踪精度，为GPS信号解算定位做好准备。

1 高动态运动对GPS信号的影响

1.1高动态下的多普勒频移

在高动态的环境下，导航接收机与高速运动的GPS卫星之间存在着径向移动，由此就会产生多普勒频移，此时L1波段载波到达接收机时的频率不再等于其发射频率(1 575.42 MHz)，而是在此频率上另加了一个多普勒频移，使得接收信号的中心频率产生偏移。

根据多普勒定律，多普勒频移计算公式如下：

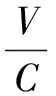
(1)

式中C表示光速，V表示卫星和载体间的相对速度，fL1表示GPS L1波段的载波频率，其值为1 575.42 MHz。载体的运动一般由速度、加速度、加加速度三个因素构成，此处相对速度V可表示为：

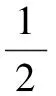
(2)

其中，vo表示初始速度，a、b分别表示加速度和加加速度。将式(2)带入式(1)，得到由卫星和载体之间的相对运动速度造成的载波多普勒频率值：

(3)

高动态运动造成载波多普勒频率增大且变化剧烈，从而导致载波跟踪环路失锁。高动态运动对码环中多普勒频率影响相对较小，只有载波的1/1 540，可通过载波辅助消除，所以，研究载波跟踪算法是GPS信号跟踪的核心，也是解决高动态的问题的关键。

1.2高动态下的GPS信号

在MATLAB环境下进行高动态轨迹模拟[4]，其模型为一直向西的变加速直线运动，如图1所示，通过改变加速度的大小，来调整多普勒频移的大小。图1(a)表示随着时间的变化，卫星加加速度也一直在变；图1(b)表示卫星的加速度；图1(c)表示卫星的运动速度，速度最快达到2 000 m/s；图1(d)表示运动所引起的多普勒频率，最大达到8 000 Hz。

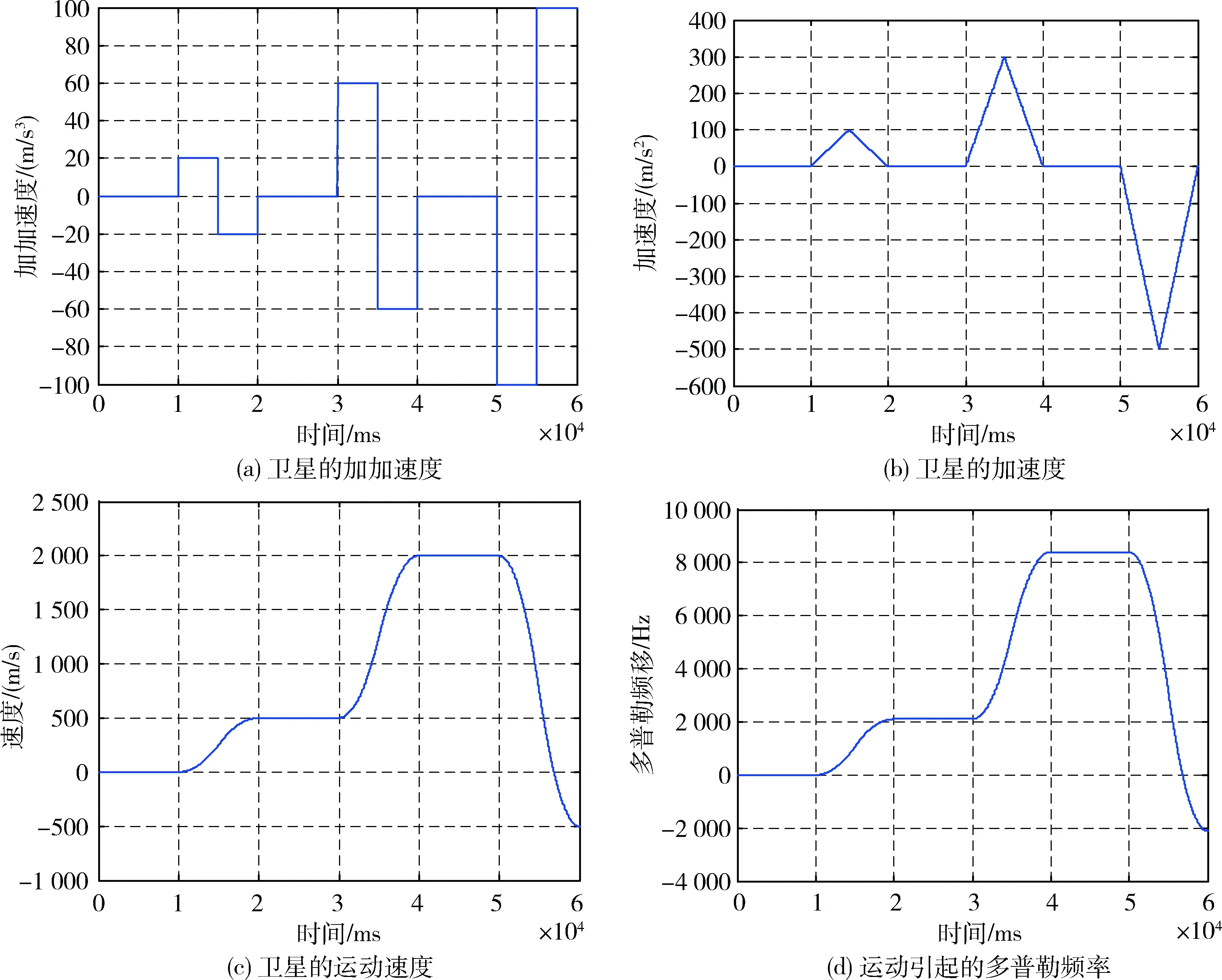
图1 变加速直线运动模型

模拟的GPS信号模型[5]可表示为：

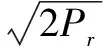
(4)

D(τ)=d[τj-ts(τj)]

(5)

C(τ)=C[τj-ts(τj)]

(6)

式中yj代表在τj时刻接收到的第j颗卫星的中频信号；Pr表示接收信号的功率；D(τ)表示的是数据码为50 Hz的导航电文调制；C(τ)表示1.023 MHz的C/A码；ωIF表示接收到的载波中频角频率；ωd表示的是接收机与卫星间的多普勒频移；φ0表示载波的初始相位值；nj表示高斯白噪声。设定载波中频为1.25 MHz，C/A码为速率为1.023 MHz基码/秒的伪随机码，D码为50 Hz的数据。三种信号使用二进制相移键控(BPSK)调制。

2 GPS信号的跟踪环路

2.1传统跟踪环路的原理

接收机的传统跟踪环路[6]的跟踪算法一般是采用二阶锁频环辅助三阶锁相环的组合环(FLL/PLL)，如图2所示。

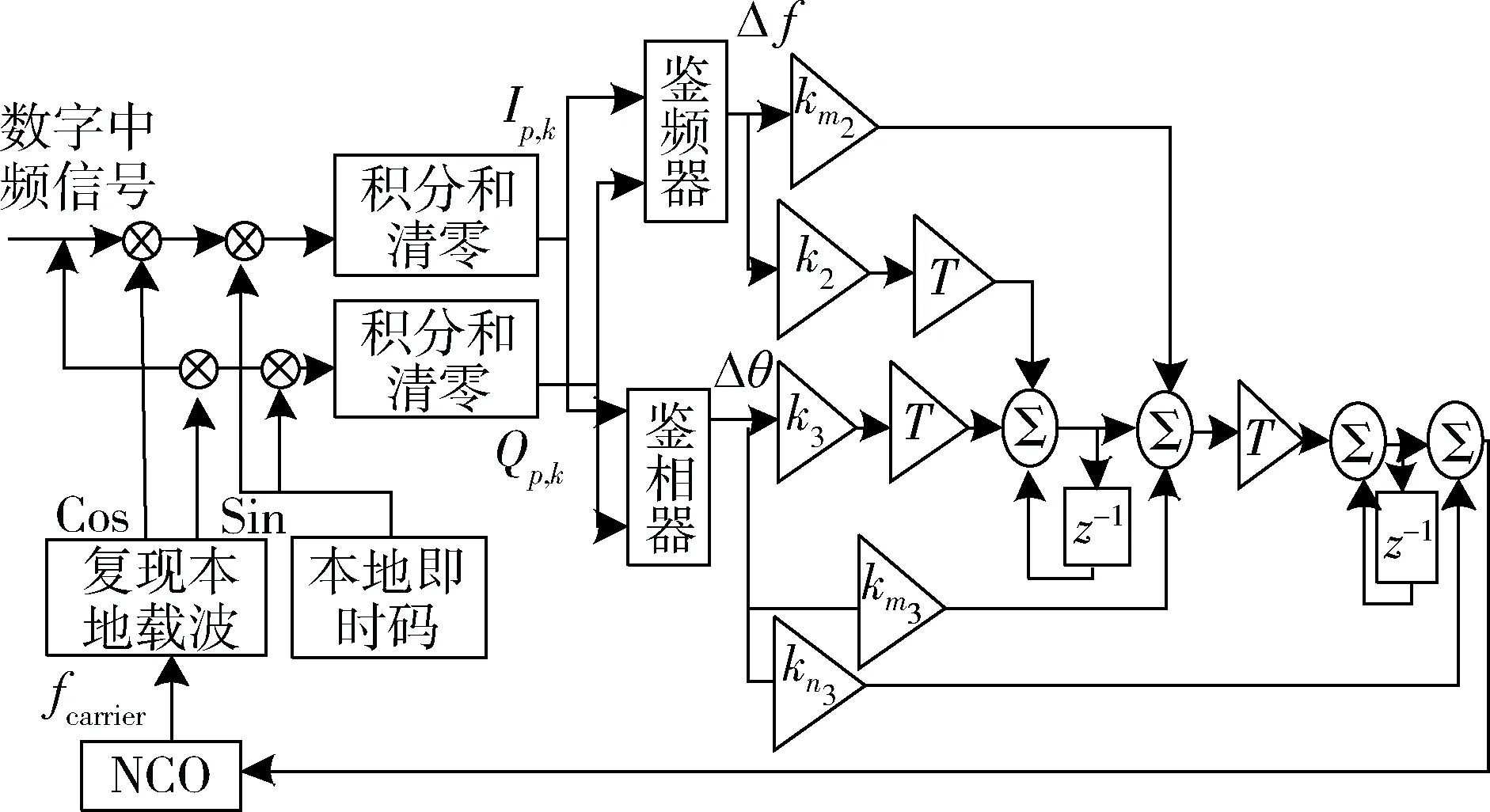
图2 二阶锁频环辅助三阶锁相环结构框图

如图2所示，二阶FLL和三阶PLL的滤波器分别使用一阶矩形滤波器和二阶矩形滤波器，环路的计算公式如下：

s0=s0+(Δθ·k3+Δf·k2)·T

(7)

s1=s1+(Δθ·km3+s0+Δf·km2)·T

(8)

fd=s1+kn3·Δθ

(9)

fcarrier=fref+fd

(10)

其中，Δθ为鉴相器的输出值，Δf为鉴频器的输出值，fcarrier为通过复合环路进行更新后的本地信号载波频率。

2.2卡尔曼滤波的原理

假设某个离散时间系统的状态方程和观测方程[7]为：

(11)

式中xk为n×1状态向量，φ为n×n状态转移矩阵，uk-1为系统输入向量，ηk-1为n×1系统状态噪声向量，zk为m×1观测向量，H为n×m观测矩阵，nk为m×1观测噪声矩阵。假设系统状态噪声{ηk}和观测噪声{nk}是相互独立的零均值白噪声序列。则得到；

(12)

其中Qk为系统状态噪声{ηk}的方差矩阵，Rk为观测噪声{nk}的协方差矩阵。

卡尔曼滤波过程如下：

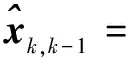
(13)

Pk,k-1=φPk-1φT+Qk-1

(14)

Kk=Pk,k-1HT(HPk,k-1HT+Rk)-1

(15)

(16)

Pk=(I-KkH)Pk,k-1

(17)

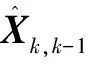
2.3扩展卡尔曼滤波器的原理

在实际情况下，系统模型通常是非线性的，经典的线性卡尔曼滤波器已不能使用，可用扩展卡尔曼滤波器(EKF)，其状态方程和观测方程为：

(18)

其中，f(·)为状态向量xk关于上一时刻状态向量xk-1的非线性函数；h(·)为观测向量zk关于状态向量xk的非线性函数。当噪声nk和ηk为零时，式(19)所对应的系统模型即“预测参考状态”，记为：

(19)

得到非线性系统的真实状态与预测参考状态的误差为：

(20)

如果这两个误差足够小，则可以将式(19)进行泰勒展开式，并取一阶近似值，得到：

δxk-1+ηk-1

(21)

(22)

将式(19)带入式(21)和式(22)中，得到：

(23)

(24)

综合上式得到离散型非线性系统的线性误差方程得：

(25)

(26)

其中φk为状态误差转移矩阵：

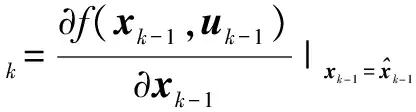
(27)

Hk为观测矩阵：

(28)

2.4扩展卡尔曼滤波器的系统模型

扩展卡尔曼滤波器的载波算法结构如图3所示。

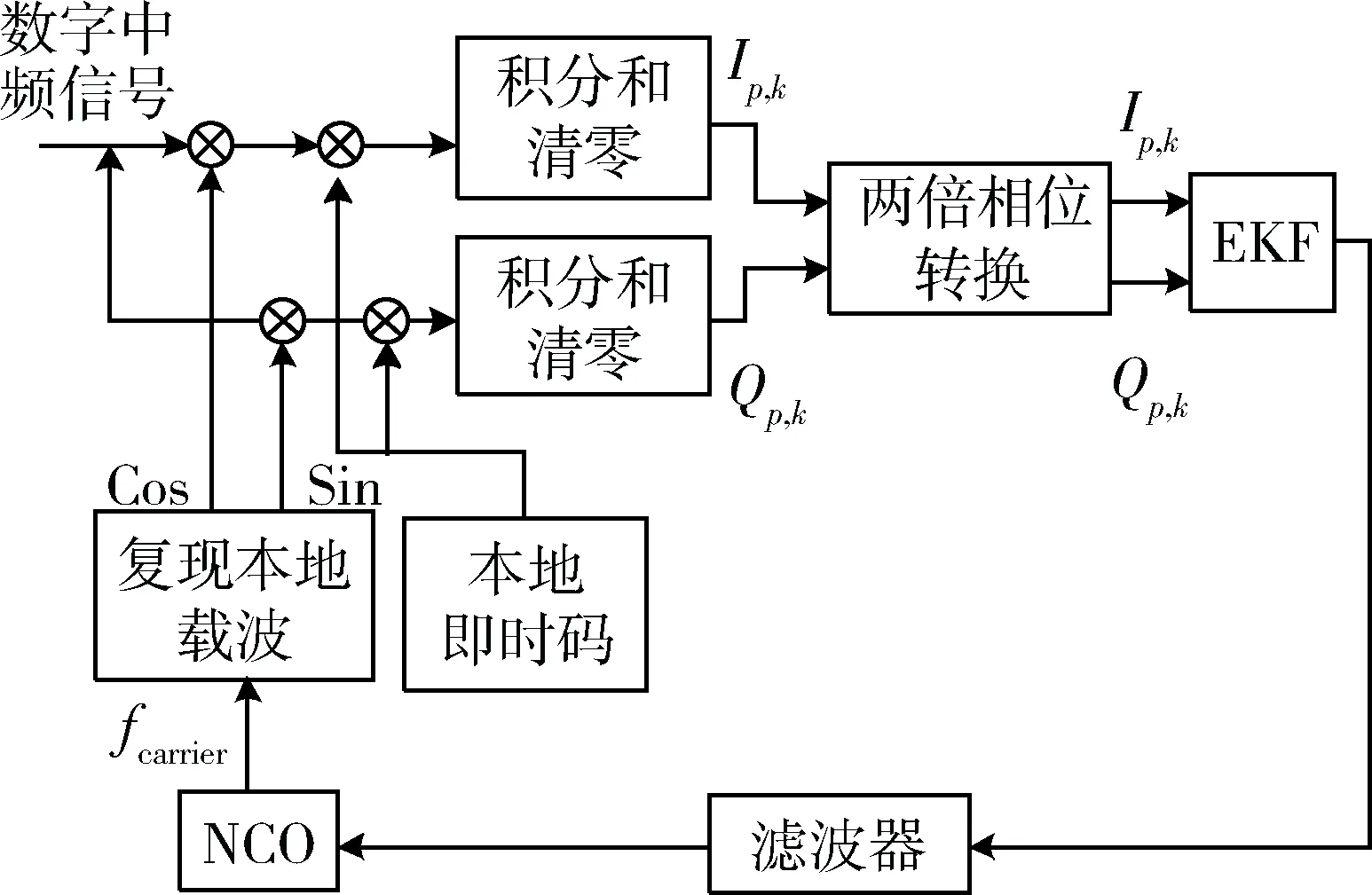
图3 EKF跟踪算法结构框图

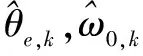
(29)

其中T为预检积分时间，ηi,k-1为系统噪声。EKF观测方程为:

(30)

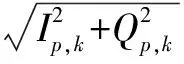
3 仿真结果

跟踪测试时，传统跟踪环路中设置预检测积分为1 ms，PLL噪声带宽为80 Hz，DLL噪声带宽10 Hz，通过仿真得到载波多普勒频移跟踪结果如图4所示，载波相位差如图5所示，其均方误差11.2°，伪距误差如图6所示，其均方差为12.5 m。

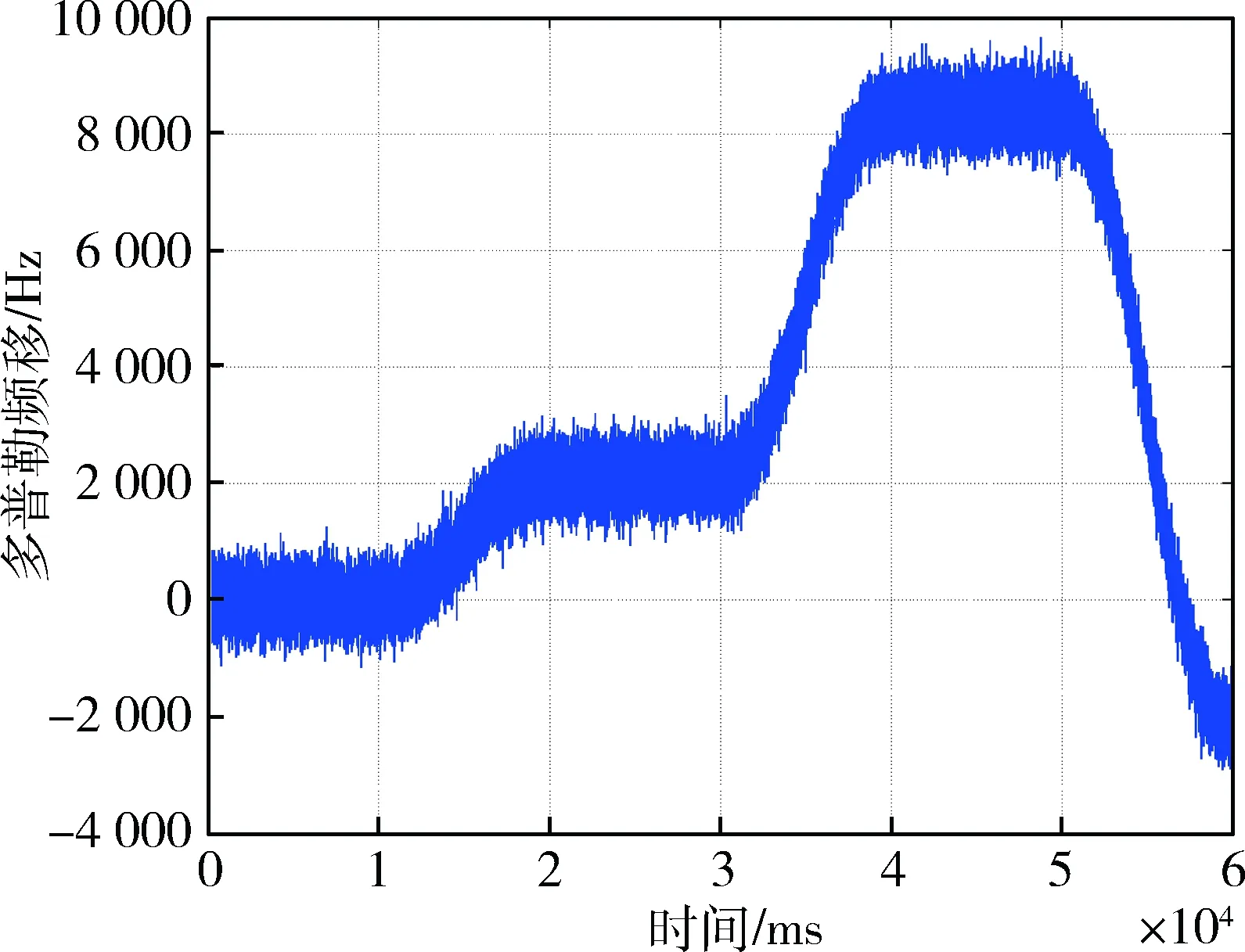
图4 传统跟踪环路得到的多普勒频率

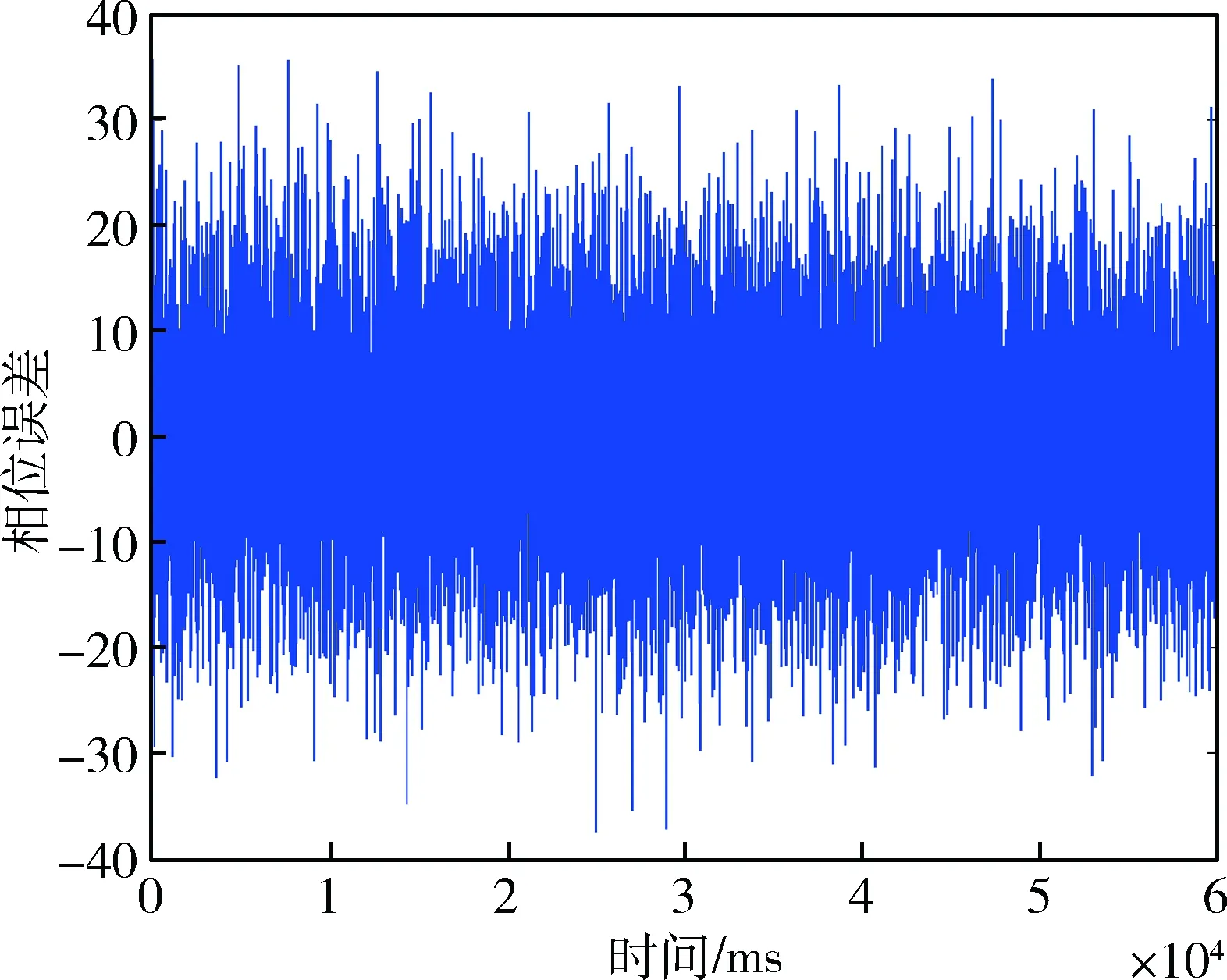
图5 传统跟踪环路的载波相位误差

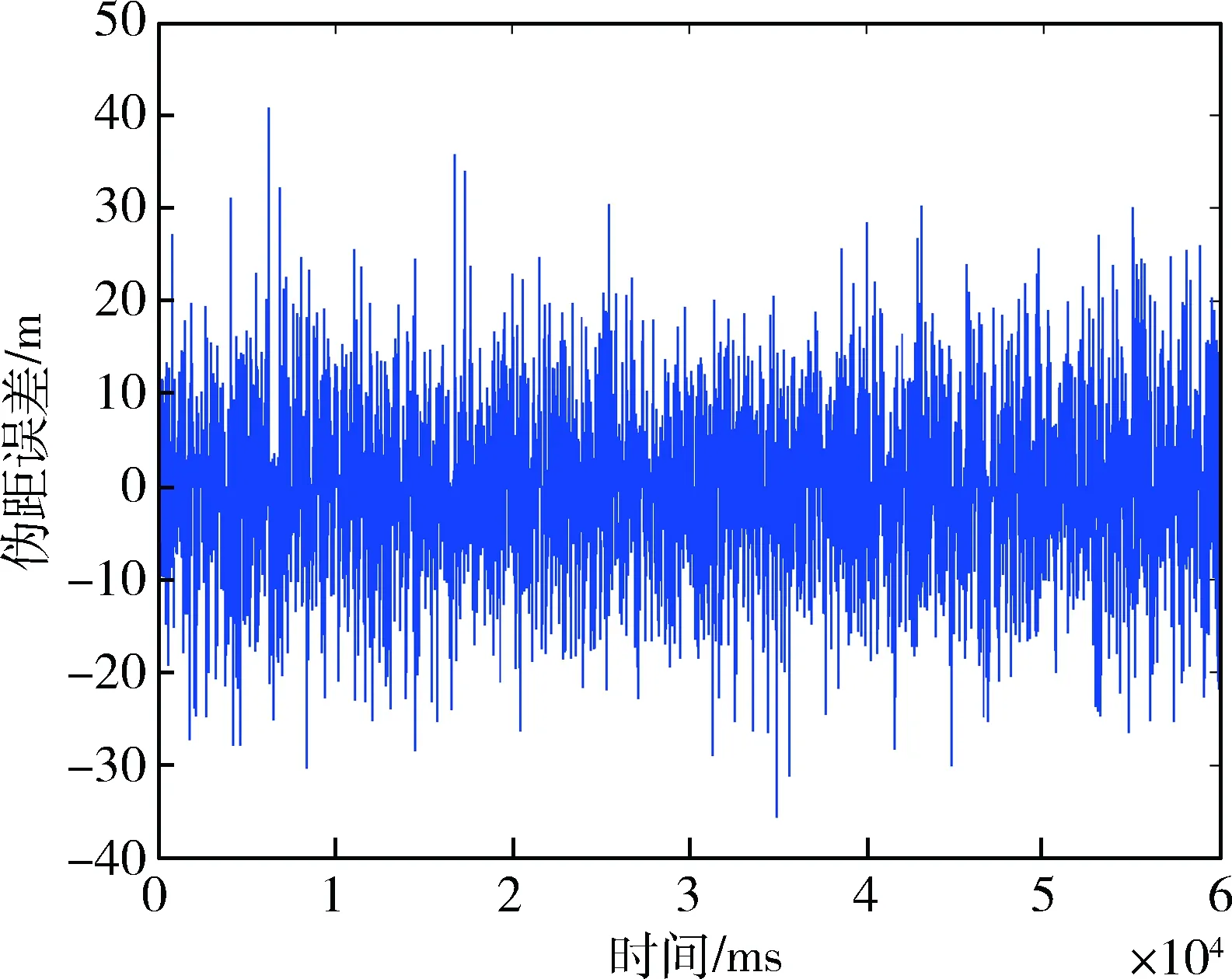
图6 传统跟踪环路的伪距误差

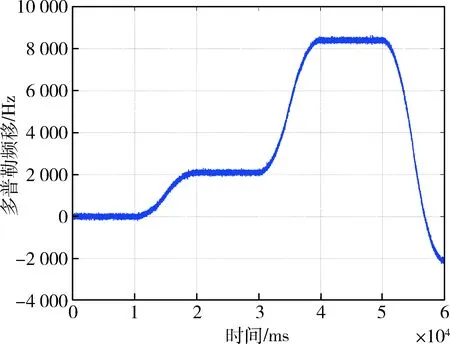
图7 EKF跟踪环路得到的多普勒频率

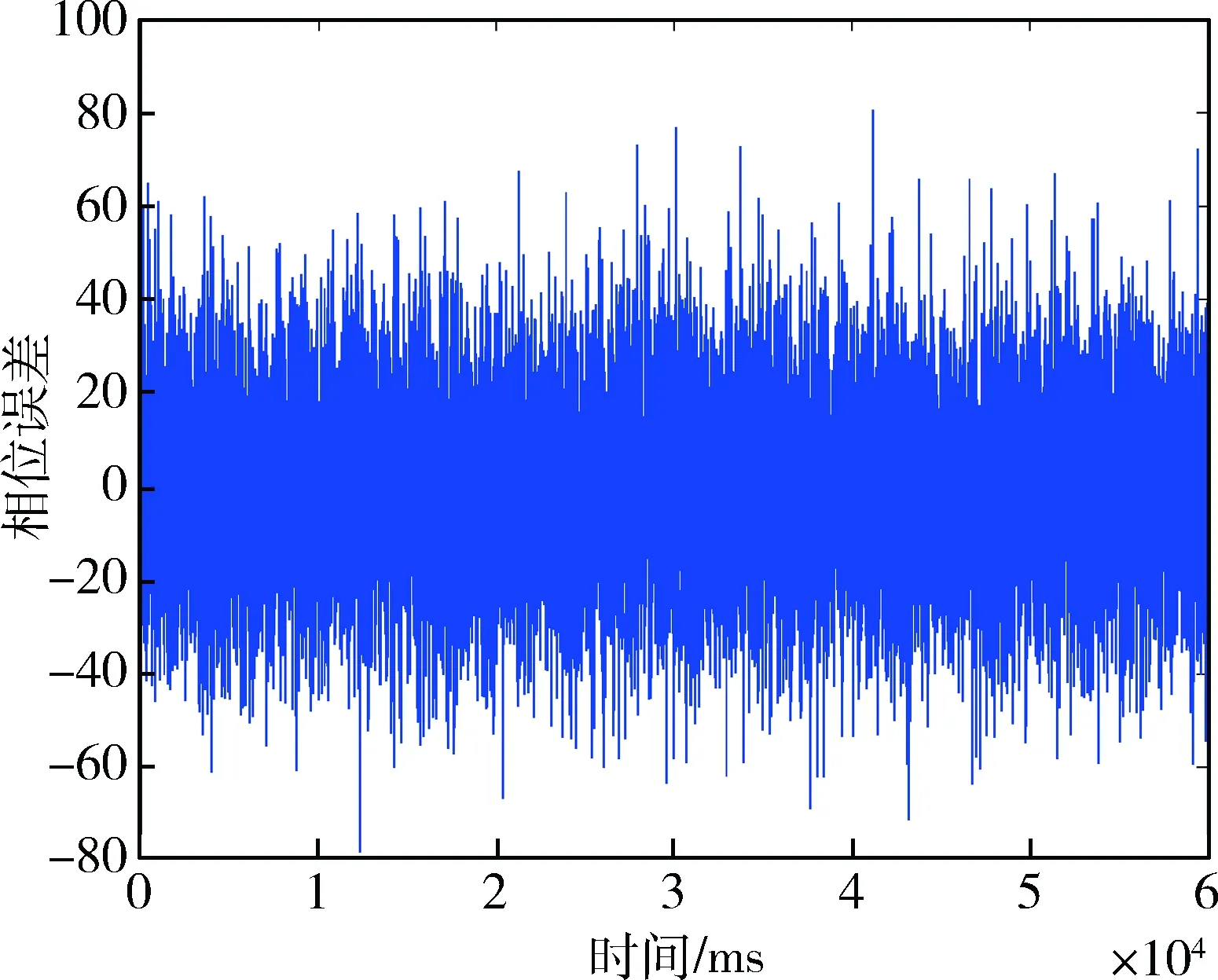
图8 EKF仿真跟踪过程中的载波相位误差

图9 EKF仿真跟踪过程中的伪距误差

4 结论

仿真结果表明，在高动态中，传统跟踪环路在提高动态性能和提高测量精度两个方面是存在矛盾的，较宽的环路噪声带宽频率使捕获带更大，有助于信号的跟踪，但此时的测量精度也会变差。扩展卡尔曼滤波跟踪环路应用观测新值不断对系统噪声和观测噪声进行递推与更新，具有较快的收敛性和较强的自适应性，还保持了较高的精度。

应用扩展卡尔曼滤波技术的GPS信号跟踪环路优于传统的跟踪环路。扩展卡尔曼滤波技术能够实现高动态跟踪技术跟踪稳定，而且精度有所提高。

[1] 毛亚青,胡展鹏,俞啸,等.基于车载GPS终端的城市环境健康监测平台设计[J].电子技术应用,2016,42(5):68-70.

[2] 徐伟,李智,王勇军.北斗/GPS无人飞行器动态导航中改进自适应算法[J].电子技术应用,2015,41(10):58-61.

[3] 费恒敏,施琴,田俊杰.INS/GPS紧耦合组合导航系统抗差定位算法[J].微型机与应用，2015,34(7):20-23.

[4] 杨俊,武奇生. GPS基本原理及其Matlab仿真[M].西安:西安电子科技大学出版社,2006.

[5] 孟繁智.高动态GPS卫星信号模拟源的关键技术研究[D].长沙:国防科学技术大学,2004.

[6] 谢刚. GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[7] 左启耀,袁洪,林宝军,等.基于Kalman滤波理论的高动态GPS信号跟踪系统仿真研究[J].系统仿真学报,2009,21(8):2160-2164.

[8] 张雪丽.基于卡尔曼滤波的高动态GPS载波跟踪算法研究[D].南昌:华东交通大学,2015.

Simulation of high dynamic GPS signal tracking loop

Wang Lili, Sun Wenpeng

(Faculty of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China)

TN961

A

10.19358/j.issn.1674- 7720.2017.18.020

王丽黎，孙文鹏.高动态下GPS信号跟踪环路的仿真研究[J].微型机与应用，2017,36(18)：66-69，72.

2017-03-17)

王丽黎(1968-)，女，副教授，硕士生导师，主要研究方向：电磁波传播、天线和智能天线。

孙文鹏(1990-)，男，硕士研究生，主要研究方向：先进导航中的信息处理。