中承式系杆拱桥吊杆疲劳性能研究

，

(1.湖南路桥建设集团有限责任公司， 湖南 长沙 410004; 2.湖南省交通科学研究院有限公司， 湖南 长沙 410015)

中承式系杆拱桥吊杆疲劳性能研究

曾东明1，黄浩2

(1.湖南路桥建设集团有限责任公司， 湖南 长沙 410004; 2.湖南省交通科学研究院有限公司， 湖南 长沙 410015)

中承式系杆拱桥是拱桥中一种常见的结构形式，吊杆作为该类型桥梁中重要的传力构件，其受力特点和疲劳性能一直是研究的热点，它关系到整座桥梁的安全和使用寿命。以湖南永州市某座中承式系杆拱桥为背景，基于车辆荷载试验和对桥梁长、短吊杆索力的不间断连续测量，通过测量数据分析发现：在集中荷载作用在主桥跨中位置时，位于支点处的短吊杆受车辆荷载影响较小；单根吊杆24 h内的应力时程曲线能反映桥梁受外界荷载影响下吊杆应力变化规律，同时能分析出桥梁1 d交通流量的分布情况；采用S—N曲线的疲劳寿命评估方法预测了吊杆疲劳寿命，并利用WEIBULL分布函数求得吊杆的疲劳可靠度，计算结果认为该桥在正常运营期吊杆已具备足够的疲劳可靠性。

系杆拱桥； 吊杆； 疲劳性能； 寿命

0 引言

中承式系杆拱桥是拱桥的一种结构形式，具有拱桥的基本特性，又有自身独有的特点。它是拱与梁两种基本结构共同组合的桥型，共同承受荷载作用，能充分发挥拱受压和梁受弯的结构性能。拱与横梁之间通过吊杆连接，拱桥吊杆主要起传递桥面系恒载和活载的作用。而吊杆作为系杆拱桥体系中最容易发生病害的构件之一，它的使用寿命关系到桥梁整体的寿命和安全。近年来，国内外不断有系杆拱桥吊杆发生破损、断裂甚至出现局部垮塌的案例[1,2]，这严重影响了大桥的使用安全。2001年11月四川宜宾小南门桥连接拱体和桥面预制板的4对8根钢缆吊杆断裂，北端长约10 m、南端长20余米的桥面预制板发生坍塌；2011年4月，新疆孔雀河大桥次短吊杆突然发生了断裂，导致主跨3道矮T梁垮塌；2012年12月四川攀枝花市区倮果金沙江大桥一根吊杆突然脱落，导致桥面出现“V”字形塌陷。诸如此类的拱桥吊杆断裂的安全事故还有很多，这让桥梁工程师们在设计、养护时愈发重视拱桥吊杆的长期性能。因此，及时针对系杆拱桥吊杆的疲劳性能进行深入研究很有必要。

1 工程概况

某中承式系杆拱桥(图1)位于湖南省永州市。该桥长659.5 m、桥面宽16 m，跨径布置为8×45 m(刚架拱)+(70+80+70)m(中承式拱)+13 m(立交通道)，原设计荷载为汽-20，挂-100。2013年该桥进行加固设计，加固后荷载等级为公路 — Ⅱ级，人群3.5 kN/m2，加固后桥面宽度为：刚架拱(2 m人行道+12 m桥面+2 m人行道)16 m；中承式拱桥(2 m人行道+1 m拱肋+12 m桥面+1 m拱肋+2 m人行道)18 m。桥梁80 m跨径主拱为抛物线型，矢跨比为1/5，吊索抗拉强度1870 MPa，理论计算截面积为2960 mm2。课题组借对桥梁进行荷载试验的机会，对被测跨径桥梁4对吊杆索力进行了不间断测量，分别为跨中一对长吊杆和支点处一对短吊杆，通过对索力变化的分析评估吊杆疲劳性能。测点布置位置如图2所示。测点编号“S”代表该吊杆位于桥梁上游一侧，“X”代表吊杆位于桥梁下游一侧。

图1 某中承式系杆拱桥

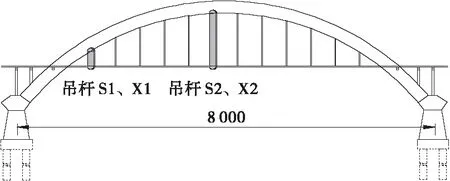
图2 吊杆测点布置图(单位： cm)

针对吊杆索力的采集，目前常用的方法一般为压力传感器测定法、磁通量法[3]和频率测试法[4]。压力传感器测定法需要在拉索锚固一端安装压力传感器，通过传感器采集到的压力计算得到索力；磁通量法则是通过拉索中电磁传感器测量磁通量的变化从而推算索力。考虑到现场实际情况和工作量，利用双通道索力动测仪采用振动频率测试法测量吊杆索力。对于两端嵌固且自由振动的吊杆而言，由于吊索的张力和其基频的平方成正比，使用索力动测仪可在采集吊索的多谐振动曲线后通过频谱分析(FFT)获取最终的索力。

2 有限元模型及静力荷载试验

2.1 有限元模型建立

根据大桥的设计情况，建立该桥的空间有限元模型。选取位于主桥中跨部分(80 m中承式拱桥)上下游对称位置的长、短吊杆各一对作为被测吊杆，考虑到连拱效应，建立了3跨有限元模型作整体分析。全桥共计134个节点，159个单元，计算模型如图3所示。

2.2 车辆静载试验结果分析

研究人员针对本座中承式系杆拱桥进行了静载试验，采用26 t汽车载重加载，共4辆车，加载车辆尺寸、载重和车型如表1所示。为了保证试验效果，对于某一特定荷载工况，试验荷载的大小和加载位置的选择采用静载试验效率系数ηq进行控制，本次加载荷载效率系数控制在1.05。加载方式为跨中三级加载，通过对跨中截面内力影响线形状的分析，在结构控制截面内力影响线上进行最不利布载，从而获得相应的结构响应，具体加载布置见图4。

图3 中承式拱桥结构离散图

表1 加载车辆情况车辆编号纵向轴距L/m轴重/kN前轴后轴总轴重1#～4#40052208260

图4 静载试验加载方案(单位： cm)

在3级静载工况下，针对拱桥S1、X1、S2、X2这4根吊杆索力进行了测试，其实测值与理论值如表2、图5所示。

静载试验结果表明： 在车辆荷载作用下，被测4根吊杆索力实测值小于理论计算值，吊杆工作正常。位于对称位置的上下游吊杆在各个工况下的索力实测值相差不大，测量最大偏差为4.2%。从结果可以分析：若综合考虑到全桥12对吊杆，则上游索力总和与下游索力总和更为接近，全桥上下游索力保持平衡。另外，根据静载试验加载工况来看，车辆荷载集中作用于桥梁跨中位置，在跨中截面最不利加载情况下，S2、X2长吊杆索力最大，S1、X1短吊杆位于桥梁支点处，远离集中荷载作用点，实测吊杆索力为长吊杆索力值80%左右，长、短吊杆在不同工况下索力变化幅度表明跨中的集中荷载对短吊杆应力影响不大。

表2 被测吊杆车辆荷载作用下索力值加载等级索力值/MPaS1吊杆X1吊杆S2吊杆X2吊杆理论值实测值理论值实测值理论值实测值理论值实测值第1级加载19461932194619262304220623042152第2级加载20001980200019702551248325512392第3级加载20201997202019832659259826592486

图5 被测吊杆静载车辆作用下的索力

3 吊杆索力时程曲线数据分析

研究人员针对该桥4根被测吊杆进行了连续索力测量，索力采集间隔为10 min 1次，采集到该桥在正常运行期间72 h内吊杆受活载作用下的索力数据，现进行数据分析。以长吊杆S2为例，筛选出1 d之内所测数据绘制成应力时程曲线见图6。

图6 S2吊杆24 h应力时程曲线

分析S2号长吊杆在1 d之内应力时程曲线图，反映了1 d之中桥梁在外界荷载作用下吊杆受力变化的规律。总体上看来，在0～400 min和1300～1440 min时间段内，吊杆应力水平要低于其他时间段，这是由于夜晚交通流量要小于白天，作用在桥梁的活荷载相对也小很多。另外，早晚的温差效应对吊杆应力也会产生影响。

4 吊杆疲劳寿命分析及预测

系杆拱桥的吊杆如斜拉索、悬索桥吊索等一样都是桥梁重要的传力构件，长期暴露在恶劣的环境当中，同时具有复杂的疲劳受力状态，针对这类构件的疲劳性能研究已经成为当前的一个热点[5,6]。拱桥吊杆由于受到活载等反复荷载的作用，在每次荷载作用之后都会产生一定量永久性的疲劳损伤，当这种疲劳损伤累积到某种程度之后，构件便会发生破损或产生裂纹。随着荷载的不断作用，由于构件局部应力集中，造成损伤进一步发展直到发生破坏，从疲劳损伤到疲劳破坏的时间由反复荷载的特性和作用次数等因素共同决定。而S—N曲线称应力-寿命曲线，一般用来评定材料疲劳寿命，本文针对拱桥吊杆的疲劳寿命分析，采用S—N曲线的疲劳寿命评估方法。

工程最常用的S—N曲线疲劳寿命评估方法是米勒(MINER)线性累积损伤理论，它认为构件每一次发生的疲劳损伤只与反复荷载的应力幅大小有关，而与其作用顺序无关[7]。也就是认为构件在疲劳损伤直到疲劳破坏的整个阶段，这个损伤都是线性可叠加的。构件疲劳寿命用N表示，为疲劳发生至疲劳破坏前构件受到反复循环荷载的次数。

本文中拱桥被测吊杆为镀锌钢丝绳，材料的抗拉强度1870 MPa。参考文献[8]，我国1860级低松弛钢绞线的S—N曲线方程为：

lgN=C-mlgΔσ

(1)

其中C=13.84，m=3.5，为试验经验确定的常数。

将式(1)两边取对数变换成为:

N=1013.84/Δσ3.5

(2)

其中: Δσ为拱桥吊杆所受到的疲劳应力幅值。

通过本次荷载试验的机会，研究人员采集了拱桥被测吊杆在72 h内的监测数据，得到测试时间内被测吊杆索力的日最大值和最小值。为了预测吊杆疲劳寿命，需要对其受到的疲劳应力幅值进行计算估计，本文以日为单位对吊杆疲劳应力幅值Δσ进行估算。由于吊杆日极值监测数据样本不足，为了保证一定的样本数量，研究人员在实测得到的日最小值和日最大值的范围内，以10%的上下限波动随机生成了27组以天为单位的极值数据，模拟桥梁被测吊杆1个月内索力数据情况。以长吊杆S2、X2为例，绘制吊杆应力极值时程曲线如图7、图8所示。

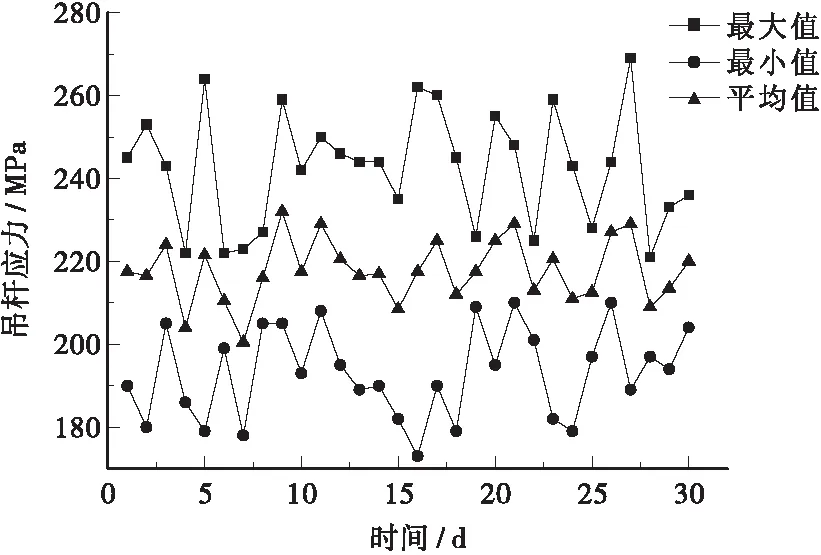
图7 吊杆S2应力极值时程曲线

图8 吊杆X2应力极值时程曲线

根据被测吊杆索力的日极值数据和Δσ的定义，将疲劳应力幅值简化成为一个吊杆应力最大值减平均值的常幅应力：

(3)

其中σimax为被测吊杆应力的日最大值;σiavg为被测吊杆应力的日平均值;n为统计时长。

把式(3)代入式(2)可得桥梁在正常运营期间被测吊杆疲劳寿命:

(4)

将吊杆应力测试数据(模拟计算周期为30 d)代入式(4)，可计算得到被测的4根吊杆在桥梁正常运营期的疲劳寿命如表3。

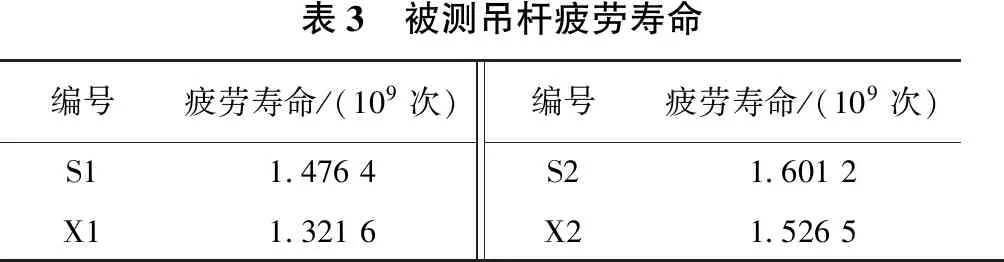
表3 被测吊杆疲劳寿命编号疲劳寿命/(109次)编号疲劳寿命/(109次)S114764S216012X113216X215265

5 吊杆疲劳可靠度分析

构件的可靠度指的是某一构件在规定的时间和条件内完成预定功能的概率。本文中，基于MINER线性累积损伤理论，考虑疲劳损伤累积，对拱桥吊杆疲劳寿命的失效概率进行评估计算。

文献[9]在韦布尔(WEIBULL)分布的基础之上，考虑到车辆或人群对桥梁产生的随机荷载以及吊杆结构受到的交变应力等情况，定义了等效应力幅值，通过雨流计数法对应力时程曲线进行统计分析，最终利用得到的等效应力幅值代入WEIBULL分布的概率密度函数，得到构件在疲劳寿命N的时间内不发生疲劳破坏的概率，即吊杆的疲劳可靠度。

同样，以吊杆S2为例，根据图6吊杆24 h应力时程曲线，利用MATLAB进行雨流计数法分析可以得到S2吊杆的等效应力幅值为17.15 MPa，将S2吊杆疲劳寿命计算结果1.601 2×109代入WEIBULL分布的概率密度函数得到吊杆疲劳可靠概率为0.999 952，再由可靠指标与失效概率的换算关系[10]从而计算得到吊杆疲劳可靠指标为3.854。经计算，拱桥被测4根吊杆的疲劳可靠指标如表4所示。

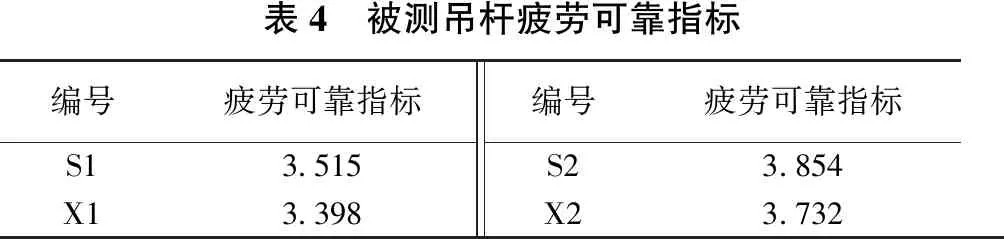
表4 被测吊杆疲劳可靠指标编号疲劳可靠指标编号疲劳可靠指标S13515S23854X13398X23732

6 结论

1) 该中承式拱桥在静力荷载作用下，通过对长、短两对吊杆索力的测试表明该桥上下游索力偏差不大，总体趋于平衡。在跨中最不利荷载作用下，位于支点处的短吊杆受影响较小。

2) 吊杆索力1 d之内的应力时程曲线图反映了桥梁受外界荷载影响下吊杆应力变化规律，在忽略温度变化对吊索应力影响后，通过该应力时程曲线能分析出桥梁1 d交通流量的分布情况。

3) 利用S—N曲线方程对拱桥吊杆疲劳寿命进行了预测。同时，利用雨流计数法求得吊杆等效应力幅值并通过WEIBULL分布函数最终求得被测吊杆的疲劳可靠度，计算结果认为该桥梁在正常运营期间吊杆已具备了足够的疲劳可靠性。

[1] 姚志强，阮小平，邓清.拱桥吊杆变形差异引发桥面断裂及类似事故的预防措施[J].公路，2002(7)：72-75.

[2] 符祥舟，何发礼，朱东生.桥面系结构形式对中下承式拱桥吊杆受力的影响[J].重庆交通大学学报(自然科学版)，2013，32(6)：1144-1147.

[3] 王荣辉，薛礼建.矮塔斜拉桥索力测试方法研究[J].中外公路，2011,31(2)116-120.

[4] 毛亚娜，刘世忠，叶丹.基于频率法对系杆拱桥吊杆索力测试的分析[J].兰州交通大学学报,2010,29(1)124-128.

[5] Y.E.Zhou.Assessment of Bridge Remaining Fatigue Life Through Field Strain Measurement[J].ASCE, Structures,2005:1-11.

[6] 孙学子.系杆拱桥吊杆的受力分析及寿命预测[D].北京：北京交通大学，2010.

[7] 李冬生. 拱桥吊杆损伤监测与健康诊断[D].哈尔滨：哈尔滨工业大学,2007.

[8] 马林.国产1860级低松弛预应力钢绞线疲劳性能研究[J].铁道设计标准，2000，20(5):21-23.

[9] 胡柏学，黄浩，曾威.基于健康监测的悬索桥吊索疲劳可靠性评估[J].公路交通科技，2015，32(6):76-80.

[10] 赵国藩，金伟良.结构可靠度理论[M].北京：中国建筑工业出版社，2000.

1008-844X(2017)03-0110-04

U 448.22+5

A

2017-08-08

曾东明(1974-)，男，工程师，从事路桥施工管理。