一种二自由度球型手腕的设计及控制分析
【作者】周锋
中国科学技术大学多智能体系统实验室, 合肥市, 230026
一种二自由度球型手腕的设计及控制分析
【作者】周锋
中国科学技术大学多智能体系统实验室, 合肥市, 230026
该文提出一种新的基于伞齿传动的二自由度球型手腕。使用三个伞齿并利用伞齿的传动特性,设计了一款两侧伞齿同向转动用于实现俯仰运动,反向转动用于实现左右摆动的二自由度球型手腕。该球型手腕具有俯仰、摆动两个自由度。通过立体几何法分析了该球型手腕的运动空间并通过齿轮传动关系分析了电机转速和球型手腕运动角速度之间的关系。使用Solidworks Motion验证了该球型手腕的运动特性并使用Matlab处理数据,呈现实验结果。实验结果表明,设计的二自由度球型手腕运动范围大,集成度高,且控制简单方便。
机器人;球型手腕;二自由度;伞齿
0 引言
机器人自诞生以来,设计的越来越精巧,但仍不能做出像人一样灵活的机器人,人体本身的结构经历千百万年的物竞天择、优胜劣汰变得十分的复杂和相当的完美,人体的四肢是重要的执行部分[1],所以对手臂的研究具有很大的价值。现在机器人手臂大部分是6个自由度的,前3个贴近于手爪的关节实现姿态控制,后3个关节实现位置控制[2]。前3个关节可称为腕关节,手腕机构按运动可分为roll-pitch-roll和roll-pitchyaw两种机构形式[3]。前者在伸展时两roll轴线共线使机构处于无法运动的状态,在运动学研究中一般称为奇异状态,因此手腕机构构型研究中后者更为多见。
传统的机器人手腕通过使用3个转动关节串联实现roll-pitch-yaw构型,可是在医疗等领域,要求机器人手腕占用空间小,操作空间大,对病人造成的创口小[4-5],所以传统的机器人手腕并不能满足要求。而且Pieper指出具有6个旋转关节的机器人存在封闭解的充分条件是相邻的3个关节轴线相交于一点[6-7]。传统的机器人手腕并不满足封闭解的充分条件,由于球型手腕本身的3个关节轴线相交于一点,所以球型手腕受到了研究者关注。
Ole. Monlang首次提出球型齿轮手腕机构,但球齿轮存在传动误差大,加工困难等问题。刘宪锋等[8]设计了一种易于加工的球齿轮手腕,但仍不能解决传动误差大的问题。潘存云等[9]使用一种新型渐开线环形齿设计了另一种球齿轮机构,大大降低了球齿轮的传动误差,但结构不紧凑。此后,研究者开始尝试寻找代替的机构实现和球齿轮手腕相同的功能。Naoki等[10]设计了一种气动肌腱来驱动二自由度球型手腕,所需气源装置占用空间大,实际可用性很低。Ikeda等[11]发明了主动万向节,并将其应用在蛇形的和仿人型的机器人手腕[12-15]中。但结构不够紧凑,控制原理也有些复杂。
本文利用伞齿轮的传递特性提出了另一种二自由度球型手腕,其结构紧凑,运动范围大,控制简单。
1 二自由度球型手腕结构
本文设计的二自由度球型手腕如图1所示。骨架为十字轴,其左右通过滚珠轴承与小臂支架相连。上下通过滚珠轴承与手爪支架相连,3个伞齿轮通过滚珠轴承套在十字轴上,两侧的伞齿轮分别通过同步带由藏在小臂中的两个电机控制,上侧的伞齿与手爪的支架固定。这样一来,当电机控制一侧伞齿轮转动时,上侧的伞齿轮将带动手爪的支架一边自转,一边公转,表现在手爪上的效果是一边做上下俯仰运动,一边做左右摆动运动。当两侧电机同速同向转动时,三个伞齿轮相对不运动,一起做俯仰运动。当两侧电机同速反向转动时,上侧伞齿轮将原地自转,表现手爪上的效果是左右摆动。
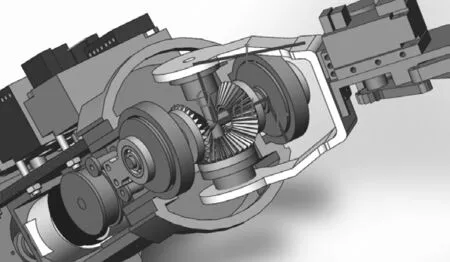
图1 二自由度球型手腕尺寸Fig.1 Size of 2-DOF spherical wrist
2 运动空间分析
在只做俯仰运动时俯仰角度范围为[-90o,90o],只做摆动运动时摆动角度范围为[-90o,90o]。标注尺寸作定量分析,如图1所示,设十字轴中心到十字轴与手爪支架连接处的距离为d,到右侧齿轮支架的距离为d1,右侧齿轮的半径为r,十字轴与手爪支架连接处与手爪的固定端的距离为L,为了理解方便,给出手腕上视图如图2,右视图如图3。当其即摆动又俯仰时,手爪支架会与两侧的机构发生运动干涉,如图3所示的1点与2点会在俯仰达到一定角度时产生碰撞。
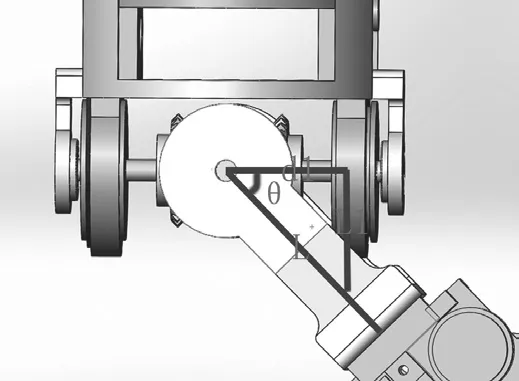
图2 二自由度球型手腕上视图Fig.2 Top view of 2-DOF spherical wrist
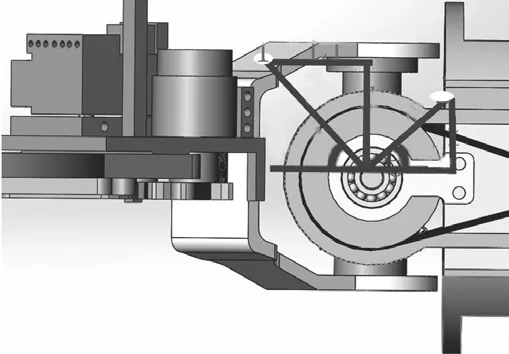
图3 二自由度球型手腕右视图Fig.3 Right view of 2-DOF spherical wrist
根据图1~图3则有如下关系:
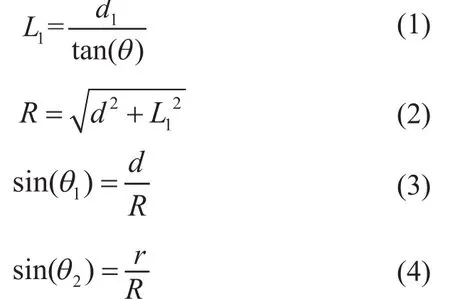
此时,俯仰角度的范围为

由于其具有对称性,先研究正向俯仰角度的变化情况,设

因为F'(θ)<0,所以随着摆动角度θ的增大,俯仰角度F(θ)减小。
本文设计的手腕尺寸为d=30 mm,d1=30 mm,r=24 mm ,代入公式可以得到以下结论:当摆动角度在[-51.343o, 51.343o]之间时,俯仰角度范围为[-90o,90o]。当摆动角度超过这个范围时俯仰角度的范围将越来越小,最小俯仰角度范围为[-36.869o, 36.869o]。人类腕关节摆动角度为[-70o, 90o],俯仰角度为[-55o, 25o][16]。当摆动时俯仰角度也会变小,在不考虑小臂旋转角度的情况下,当人的手腕摆动到极限位置时,俯仰角度几乎为零,故本文设计的二自由度球型手腕运动范围满足要求。
3 电机转速与球型手腕的俯仰、摆动角速度的映射关系
如图1所示,设左侧齿轮为齿轮1,右侧齿轮为齿轮3,上侧齿轮为齿轮2,齿轮2的同心轴即十字轴的竖轴为杆H,十字轴的横轴为杆V。为了研究和理解方便,规定:齿轮1从左视图看顺时针旋转为正方向,齿轮2从上视图看顺时针旋转为正方向,齿轮3从右视图看逆时针旋转为正方向。杆H从右视图看绕杆V逆时针旋转为正方向。
由于齿轮2的运动并不是绕定轴线的运动,所以齿轮1、2、3之间的传动比不能直接使用定轴轮系的方法来求解[17]。
设w1、w2、w3及wH为齿轮1、2、3及杆H的绝对角速度,使用相对运动原理,给原有轮系加一个公共的角速度“-wH”,原有的轮系中各构件的传动比不变。加上公共的角速度“-wH”后,各构件的角速度如表1所示。

表1 各齿轮相对角速度Tab.1 The relative angular velocity of every gear
表中=wH-wH=0,说明系杆H静止不动,此时的相对轮系为定轴轮系了。此时,轮系中任意两轮的传动比可用定轴轮系的方法求得,设z1,z2,z3为伞齿轮1,2,3的齿轮数,为轮系中齿轮1与齿轮2的传动比即角速度关系,为轮系中齿轮1与齿轮3的传动比即角速度关系。则有,

其中wH为公转角速度,为自转角速度。
因为公转引起手腕的上下俯仰转动,自传引起手腕的左右摆动转动,所以w俯仰=wH,w摆动=,本文设计的手腕中的z1:z2:z3=1:1:1所以

4 角速度映射关系验证实验
本文首先使用Solidworks Motion对二自由度球型手腕进行运动仿真,然后使用Matlab处理仿真的数据,呈现运动关系。
(1)首先固定齿轮1不动,齿轮3以60o/s的角速度转动,运动6 s,齿轮3转动一周,顶部齿轮2一边绕十字轴的横轴V公转,一边绕十字轴的竖轴H自转,公转角速度即相对X轴的角速度(也是手腕俯仰角速度)见图4。
在忽略仿真计算误差的情况下,由图4可以看出,俯仰角速度为30o/s。
相对Y轴和Z轴的角速度见图5。
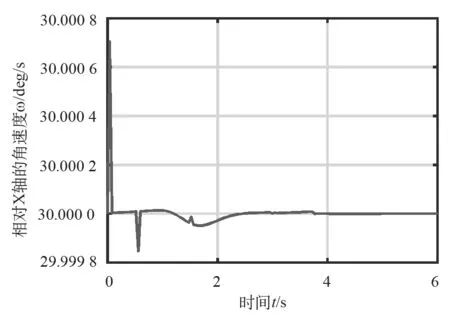
图4 单边转动-相对X轴角速度Fig.4 Only one side rotate-opposite x axis angular speed
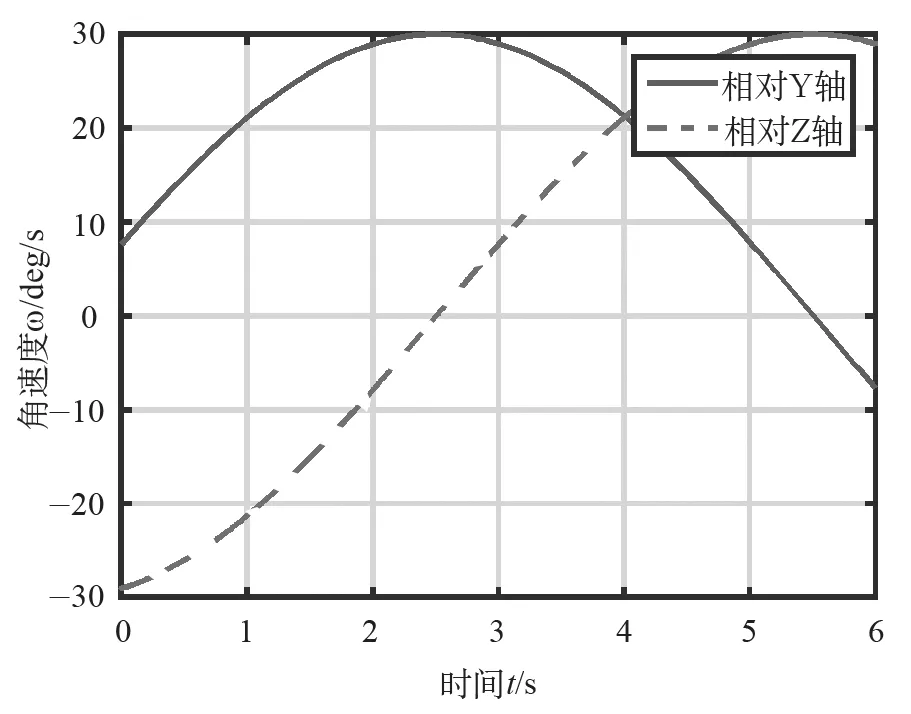
图5 单边转动-相对Y, Z轴角速度Fig.5 Only one side rotate-opposite Y, Z axis angular speed
由图5可知,自转角速度即摆动角速度相对Y轴和Z轴的角速度都是不断变化的,这是由于其在公转的原因,导致在Y轴和Z轴的分量在不断变化,但其自转角速度是稳定的,我们使用Matlab求其合速度,并作图6。

图6 单边转动-Y, Z轴角速度的合速度Fig.6 Only one side rotate-resultant velocity of Y, Z axis angular speed
在忽略仿真计算误差的情况下,由图6可知,其自转角速度为30o/s。满足角速度映射关系。
(2)让齿轮1和3都以60o/s的角速度转动,按照以上步骤计算俯仰角速度和摆动角速度见图7。
由图7可以看出,齿轮1和3同向转动时,手腕只做俯仰运动,俯仰角速度大小为60o/s。满足角速度映射关系。
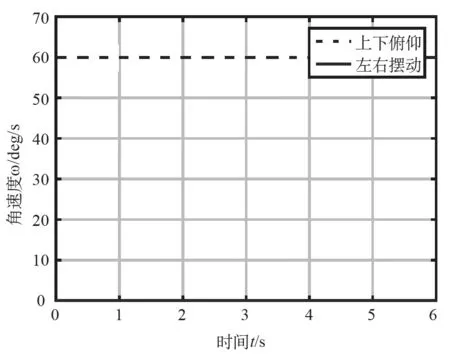
图7 同速同向转动Fig.7 Same speed and same orientation rotate
(3)让齿轮1以-60o/s的角速度转动,齿轮3以60o/s的角速度转动,按照以上步骤计算俯仰角速度和摆动角速度见图8。

图8 同速反向转动Fig.8 Same speed and inverted orientation rotate
由图8可以看出,齿轮2原地转动即手腕摆动,摆动角速度为60o/s,满足角速度映射关系。
(4) 让齿轮3转动角速度120o/s,齿轮1转动角速度为30o/s,按照以上步骤计算俯仰角速度和摆动角速度见图9。
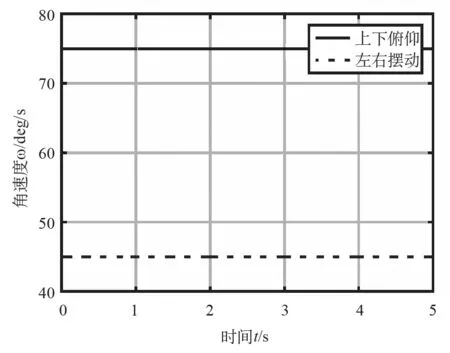
图9 不同速转动Fig.9 Different angular speed rotate
得到俯仰角速度75o/s,摆动角速度为45o/s,至此,验证本文理论。
4 结论
本文在分析借鉴前人对球型手腕研究的基础上,利用伞齿轮传动原理,巧妙地设计了一种结构更加简单紧凑、控制更加方便的二自由度球型手腕,并通过相对运动原理得出了电机转动角速度和球型手腕俯仰、摆动角速度之间的角速度映射关系。实验结果表明,该球型手腕运动范围远远大于人的手腕运动范围,相比其他球型手腕具有结构紧凑,控制简单的优势。
该球型手腕灵活度高,控制简单,在微创医疗领域和家庭服务机器人领域具有很好的应用前景。下一步将把该手腕应用在六自由度串联机械臂中,分析其在机器人手臂运动规划中的特性。
[1] 杜金霞. 仿人臂通用机器人研究[D]. 兰州:兰州理工大学,2008.
[2] Siciliano B, Khatib O. Springer Handbook of Robotics[M]. Berlin,UK: Springer-Verlag, 2007.
[3] 吴伟国, 邓喜君, 蔡鹤皋. 基于直齿轮传动和双环解耦的柔性手腕原理与运动学分析[J]. 机器人, 1998, 20(6), : 433-436.
[4] 戴建生, 魏武国, 李建民. 国际微创手术机器人的现状和发展趋势[J]. 机器人技术与应用, 2011, 4 (8): 1-5.
[5] 宋晓峰, 谈士力. 微型机器人的发展和研究现状[J]. 机床与液压,2004(8): 1-2.
[6] Pieper D, Roth B. The kinematics of manipulators under computer control[C]. 2th Int Cong Theory Mach Mechan. 1969(2): 159-169.
[7] Pieper D. The kinematics of manipulator under computer control[D]. California, USA: Stanford University, 1968.
[8] 刘宪锋, 潘存云, 杨昂岳, 等. 基于球形齿轮传动的柔性手腕动作原理及其运动分析[J]. 机器人, 1996, 18(4): 201-205.
[9] 潘存云, 温熙森. 基于渐开线球齿轮的机器人柔性手腕结构与运动分析[J]. 机械工程学报, 2005, 41(7): 141-146.
[10] Naoki S, Norihiko S, Toshiyuki S. Development of spherical joint robot using pneumatic artif i cial muscles[C]. Proc 34th Ann Conf IEEE Indust Electr Soc, 2008: 1614-1619.
[11] Ikeda H, Takanashi N. Joint assembly moveable like a human arm,United States: 4683406 [P]. 1987-07-28.
[12] Eric P, Timothy O, Samad H. The JPL serpentine robot:a 12-DOF system for inspection[C]. Proc IEEE Int Conf Robotics Automation. Nagoya, Japan: IEEE, 1995: 3143-3148.
[13] Asano K, Obama M, Arimura Y. Multijoint inspection robot[J].IEEE Trans Indust Electr, 1983, 30(3): 277-281.
[14] Nilsson M. Snake robot, free climbing[J]. IEEE Contr Syst Mag,1998, 18(1): 21-26.
[15] Albert A, Sven B, Jens O, et al. Upper body of a new humanoid robot-the design of ARMAR Ⅲ[C]. Proc IEEE-RAS Int Conf Humanoid Rob, 2006: 308-313.
[16] 朱秋国. 仿人机器人结构设计与分析[D]. 杭州: 浙江大学,2011.
[17] 庞振基, 黄其圣. 精密机械设计[M]. 北京: 机械工业出版社,2014.
Design and Control Analysis of 2-DOF Spherical Wrist
【 Writer 】ZHOU Feng
Multi-Agent Systems Lab, University of Science and Technology of China, Hefei,230026
In this paper, a novel design of a 2-DOF spherical wrist which is based on umbrella gear transmission is proposed.Using three umbrella gear and their attribute, a 2-DOF spherical wrist is designed to have the capability to pitch move when bilateral umbrella gear homodromous rotation and swing move when bilateral umbrella gear inversus rotation.This spherical wrist has two degree of freedom which can pitch and swing. Through constructive solid geometry, the spherical wrist’s motion space is analyzed. Moreover, through the gear transmission relationship, the relation between the spherical wrist’s angular velocity and the electromotor’s angular speed is established. Using the software of Solidworks Motion to verify motion characteristics and Matlab to analyze experimental data and achieve experimental results. The experimental results show that the 2-DOF spherical wrist has large range of movement and high integration. Moreover, it’s convenient to control the wrist.
robot, spherical wrist, 2-DOF, umbrella gear
TP241
A
10.3969/j.issn.1671-7104.2017.05.006
1671-7104(2017)05-0334-04
2016-12-05
教育部博士点基金(20133402110026)
周锋,E-mail: zf062@mail.ustc.edu.cn

