门式钢框架结构非线性爆炸响应

魏德敏，黄启超

（华南理工大学 土木与交通学院，广东 广州 510640）

门式钢框架结构非线性爆炸响应

魏德敏，黄启超

（华南理工大学 土木与交通学院，广东 广州 510640）

采用ALE多物质流固耦合方法模拟爆炸荷载，对门式钢框架结构在内部爆炸荷载作用下的动力响应全过程进行了计算分析。分析中考虑了爆炸源的水平爆距和放置高度对框架结构动力响应的影响。研究结果表明，当爆炸源的放置高度较低时，水平爆距对框架柱的动力响应影响较大，而对框架梁响应影响较小；当爆炸源的水平爆距一定时，框架梁的动力响应随着爆炸高度的提高而增大。通过计算结果的分析对比得到使框架结构发生最大响应的最不利爆炸位置。

爆炸荷载；钢框架；非线性响应

0 引言

近年来，由于突发事件引发的爆炸事故给土木工程结构以及人们的生命财产造成了巨大损害，然而关于工程结构在爆炸冲击荷载作用下的破坏机理及强非线性动力响应的研究成果相对较少，大多数研究者研究的重点是工程结构在自然灾害作用下的响应及破坏。因此研究工程结构在爆炸荷载下的非线性动力响应是非常必要的。

目前钢结构在工业和民用建筑中应用广泛，关于钢结构在爆炸荷载下的动力响应及破坏机理已有一些研究成果。Amr等[1]对钢梁在不同当量炸药爆炸下的动力响应进行了试验研究。Al-Thairy[2]对承受横向爆炸荷载的钢梁提出了单自由度分析模型。Oskouei等[3]针对不同形式的钢板在爆炸荷载下的动力响应进行了数值分析，发现边界条件对钢板的响应影响较大。Abdallah等[4]利用延伸率来估算钢柱爆炸响应的损伤水平。Zhai等[5]研究了不同跨高比Kiewitt-8单层钢网壳在爆炸荷载下的动态响应模式。丁阳等[6]对钢框架结构的爆炸响应进行了分析，得到结构发生局部破坏以及连续倒塌的炸药量。Coffield等[7]对几种按抗震规范设计的不规则钢框架在爆炸荷载作用下的动力响应进行了理论分析，发现同心支撑框架有更好的抗爆能力。文献[8]分析了某钢框架结构在爆炸荷载下的倒塌过程，得出梁柱节点产生塑性变形后框架柱失去承载能力，从而导致结构倒塌的结论。宋拓等[9]分析了五层钢框架结构的非线性爆炸响应，发现楼板对结构的连续倒塌性能有很大影响。张秀华等[10]分析了燃气爆炸下钢框架结构的破坏模式，给出结构破坏模式与跨数和层数的关系。李海旺等[11]对单榀钢框架在爆炸荷载作用下的变形形态进行了有限元分析，分析中考虑了荷载峰值和爆炸作用时间的影响。

本文对门式钢框架结构在内部爆炸荷载作用下的非线性动力响应进行理论分析。采用流固耦合方法[12]（Arbitrary Lagrange Euler）对爆炸冲击波在空间的传播效应进行了数值模拟，分析了爆炸源水平爆距和放置高度对框架结构非线性响应计算结果的影响，并通过计算对比得到使结构产生最大响应的最不利爆炸位置。

1 计算模型

1.1 几何构形

本文研究的门式钢框架结构净跨L=4m，净高H=3m，爆炸源放置框架内部，水平爆距S为爆炸源与左柱的水平距离，放置高度HB为爆炸源与地面的垂直距离。框架结构的柱与梁均为工字型截面，框架柱的截面高度×翼缘宽度×腹板厚度×翼缘厚度为HW300×300×10×15，框架梁的截面高度×翼缘宽度×腹板厚度×翼缘厚度为HM294×200×8×12。框架柱与基础的连接为固定约束，梁与柱的连接视为刚性连接。结构的几何构形如图1所示。

图1 框架结构几何构形Fig.1 Geometry model of the frame structure

1.2 材料模型

本文考虑的炸药爆炸当量B=40kg，密度为1.63g/cm3，爆炸速度为6930m/s，初始爆炸压力为21GPa[13]，利用LS-DYNA程序的高能炸药模型（*MAT-HIGH-EXPLOSIVE-BURN）模拟爆炸源，用JWL状态方程描述爆炸压力P[14]，状态方程的数学表达式为：

其中，V为相对体积，E0为初始单位体积内能，ω，A，B，R1，R2为材料参数。

JWL状态方程中的材料参数一般是在炸药圆筒试验基础上通过数值模拟得出的。本文参照文献[15]选取表1所示材料参数。

表1 炸药材料参数

框架结构的钢材为Q235，其初始屈服应力0σ=235MPa，弹性模量E和切线模量Et分别为206GPa和2.06GPa，泊松比v=0.3。由于应变率效应，钢材的动态屈服应力一般高于其静态屈服应力。本文分析中对钢结构材料采用可以考虑应变率效应的Cowper-Symonds塑性随动强化本构模型：

其中，yσ为考虑应变率效应后的屈服应力，0σ为初始屈服应力，ε˙为应变率，C=40和P=0.5为选定的应变率参数。另外，本文取钢材的破坏失效应变FS（Failure Strain）为0.2[16]。

1.3 有限元模型

钢框架结构单元采用拉格朗日算法实体单元，炸药与其爆炸物质流动空间（空气）采用欧拉算法实体单元。拉格朗日单元耦合在欧拉单元之中，炸药起爆后产生的爆炸冲击波在欧拉单元中流动，爆炸冲击波对结构的作用可用多物质流固耦合方法来实现。地面考虑为刚性地面，流动空间采用无反射边界条件，冲击波在边界流出而无反射如图2所示。

2 结构的爆炸响应

2.1 水平爆距的影响

本节分析爆炸源放置高度HB=0.00m，水平爆距S变化时对钢框架结构整体动力响应的影响。

图2 有限元分析模型Fig.2 Analysis model of finite element method

表2给出水平爆距S=2.00m，1.50m，1.00m，0.80m和0.50m时，左框架柱受到的爆炸峰值压力最大值及其出现时间和位置。由表中计算结果可知，当爆炸物的放置高度不变时，爆炸源位置越接近左柱，左柱的峰值压力最大值越大，出现的时间T1越早，压力持续时间t0越短，最大压力出现的位置越靠近柱底。

表2 左柱最大爆炸压力（S变化）

表3给出右框架柱受到的爆炸峰值压力最大值及其出现的时间和位置。由表3发现，当爆炸物的放置高度不变时，爆炸源离右柱越远，右柱的峰值压力最大值越小，出现的时间T1越晚，压力持续时间t0越长，最大压力出现的位置越靠近柱顶。

表3 右柱最大爆炸压力（S变化）

表4给出框架梁受到的爆炸峰值压力最大值及其出现时间和位置。由表4可知，当爆炸物的放置高度不变时，水平爆距的变化对框架梁的最大爆炸压力值及其出现时间影响较小，最大压力出现的位置随水平爆距的减小逐渐靠近梁左端。

表4 框架梁最大爆炸压力（S变化）

图3给出水平爆距S=0.80m时框架结构的最终变形示意图。由图3看出，左柱的变形主要集中在柱子下部；右柱的变形为水平侧移，侧移最大值发生在柱顶；框架梁发生向上的位移，跨中位移值最大。

图3 结构最终变形示意图（S=0.80m）Fig.3 Permanent deformation of structure （S=0.80m）

表5给出水平爆距变化时框架结构的最终位移最大值以及出现位置，表中框架柱水平位移向右为正，框架梁挠度向上为正。由表5可知，左框架柱的最大水平位移发生在柱高h=0.60m处，最大位移值随水平爆距的减小而增大；右框架柱的最大水平位移发生在柱顶，但其方向将随爆距变化改变；框架梁的最大挠度发生在跨中，挠度值随水平爆距的减小而增大。结构的变形主要集中在左柱，左柱的最大位移值远大于右柱和框架梁。

表5 框架结构最终变形（S变化）

图4 框架结构塑性变形区（S变化）Fig.4 Plastic deformation distribution of frame structure（Schanges）

图4为水平爆距变化时框架结构的塑性变形分布情况。由图4看出，框架结构的塑性变形主要分布在框架柱的柱底和柱顶区域。随着水平爆距的减小，左柱柱底的塑性变形区向柱顶方向快速扩展，而右柱的塑性变形区逐渐缩小。水平爆距减小到一定程度，右柱柱底不会出现塑性变形。

表6 结构最大塑性应变（单位：×10-2）

表6给出水平爆距变化时各构件的最大塑性应变值。由此可知，左柱柱顶和柱底的塑性应变值随水平爆距的减小而增大，右柱柱顶的塑性应变值随水平爆距的减小而减小，右柱的塑性应变值明显小于左柱。水平爆距减小到0.50m时，左柱柱底的塑性应变最大值达到0.2542，超过了材料的失效应变。

2.2 爆炸源竖向高度

本节考虑爆炸源水平爆距S=2.00m，放置高度HB变化时对框架结构动力响应的影响。

表7和表8分别给出爆炸源在结构对称轴上不同高度时左框架柱和框架梁受到的峰值压力最大值及其出现时间和位置。

表7 左柱最大爆炸压力（HB变化）

表7和表8分别给出爆炸源在结构对称轴上不同高度时左框架柱和框架梁受到的峰值压力最大值及其出现时间和位置。

由表7可知，爆炸源高度在0至2.5m范围变化时，左柱爆炸压力持续时间和峰值压力最大值出现的时间变化不大，分别为8.54ms和0.95ms左右。爆炸源高度HB为1.50m时，峰值压力达到最大值1.64MPa。表8表明，框架梁的爆炸峰值压力最大值出现在跨中，且随爆炸源高度的提高而增大，峰值压力持续时间和最大值出现的时间则随着爆炸源高度的提高而减小。

表8 框架梁最大爆炸压力（HB变化）

图5给出爆炸源对称放置在高度HB=2.00m处框架结构的最终变形示意图。由图5可以看出，爆炸源位于框架结构的对称轴时，结构的最终变形基本上是对称的，框架柱的最终水平位移方向向外，框架梁的最终挠度方向向上。

由表9给出的框架结构最终位移最大值以及出现位置可知，框架柱侧移最大值出现的位置随爆炸源高度的增大而提高，爆炸源高度HB=1.50m时，框架柱的水平位移响应最大；框架梁跨中最大挠度值远大于框架柱的侧移最大值，且随着爆炸源高度的提高而明显增大。

图5 结构最终变形示意图（HB=0.80m）Fig.5 Permanent deformation of structure （HB=0.80m）

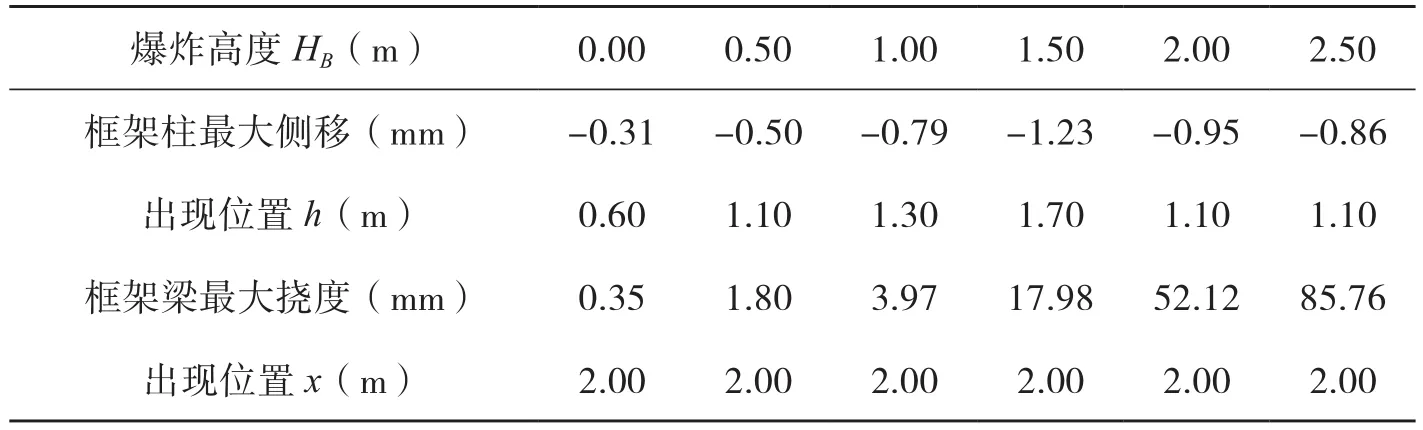
表9 结构最大位移值（HB变化）

图6 结构塑性变形区（HB变化）Fig.6 Plastic deformation distribution of structure（HBchanges）

图6为爆炸源高度变化时框架结构的塑性变形情况。由图6可以看出，框架柱的柱底及梁柱节点区域内侧最先产生塑性变形，随着爆炸源高度的提高，框架梁端部和跨中相继进入塑性变形区，且框架梁的塑性变形区面积扩展相对较快，而框架柱柱底的塑性变形区面积明显缩小。

表10给出框架结构塑性变形区的最大塑性应变值。由表10可知，随着爆炸高度的提高，框架柱底部塑性变形区的塑性应变最大值减小，柱顶塑性变形区的塑性应变最大值增大；当爆炸源高度HB≥2.00m时，框架梁跨中塑性应变最大值超过材料的失效应变（FS=0.2）

表10 结构最大塑性应变（单位：×10-2）

2.3 爆炸的最不利位置

以上分析了框架结构内部爆炸源的爆距和高度变化对结构非线性响应的影响，图7和图8给出结构最大位移值Umax与这两个影响因素的关系曲线。

图7 最大位移与爆距关系曲线（HB=0.00m）Fig.7 Umax～Srelationship curves（HB=0.00m）

图8 最大位移与爆炸高度关系曲线（S=2.00m）Fig.8 Umax～HBrelationship curves（S=2.00m）

从结构位移响应方面分析，爆炸源位于地面（HB=0.00m）时，水平爆距变化对框架柱的水平位移响应影响较大，其水平位移响应最大值随着爆距的减小而增大。爆炸源位于结构中轴线（S=2.00m）时，爆炸源高度变化对框架梁的竖向位移响应影响较大，其竖向位移响应值随着爆炸源高度的提高而增大，而框架柱水平位移在高度HB=1.50m时达到最大值。从结构塑性应变方面分析，水平爆距减小到S=0.50m时框架柱最大塑性应变值达到失效应变；而爆炸高度增加到HB=2.00m时框架梁最大塑性应变值达到失效应变。

通过结构位移和塑性应变响应判别爆炸影响最不利位置（以结构左半侧空间为考虑范围），在结构达到失效塑性应变时，爆炸源在框架结构内部的最不利爆炸位置有两个，一是使框架柱产生最大水平位移响应的位置：S=0.50m，HB=1.50m；二是使框架柱和框架梁均产生最大位移响应的位置：S=0.50m，HB=2.00m。

图9 结构最终变形（爆炸位置①）Fig.9 Final deformation of structure （Explosive location①）

图9给出爆炸源在最不利爆炸位置①（S=0.50m，HB=1.50m）时，框架结构的最终变形示意图。由图9不难看出，最不利爆炸位置①时，左柱最终侧移的最大值发生在柱子中部（h=1.50m）；右柱最终侧移的最大值发生在柱顶（h=3.00m）；框架梁最终挠度的最大值发生在距梁左端x=0.50m处。

图10给出爆炸源在最不利爆炸位置①时，框架柱的最大水平位移和框架梁最大竖向位移响应时程曲线，这些最大位移值Umax及其最终稳定值Ur以及出现的时间T1和T2如表11所示。

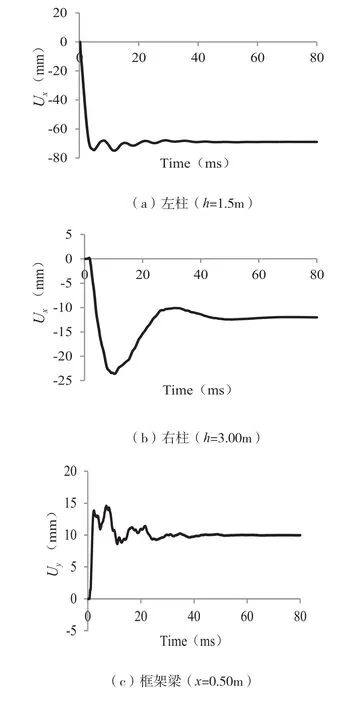
图10 结构最大位移响应（爆炸位置①）Fig.10 Umax of the structure（Explosive location①）

表11 位移响应计算结果（爆炸位置①）

由图10和表11可以看出，在最不利爆炸位置①时，左柱的水平位移响应相对较大，其最大值和最终值分别为80.64mm和74.15mm；其次是右柱，其最大值和最终值分别为17.09mm和9.97mm；框架梁的竖向位移响应值较小，其最大值和最终值分别为14.56mm和9.26mm。左柱水平位移响应的最大值与最终值分别是右柱的4.72倍和7.44倍，是框架梁的5.54倍和8.01倍。

图11给出在最不利爆炸位置①时，框架结构的塑性变形区，表12给出这些塑性变形区的最大塑性应变值。

图11 结构塑性变形区（爆炸位置①）Fig.11 Plastic deformation of the structure（Explosive location①）

由图11可知，爆炸源在最不利爆炸位置①时，框架结构的塑性变形集中在左柱柱底，左柱中部，左柱柱顶和框架梁左端，而右柱未发生塑性变形。表12的计算结果表明，最不利爆炸位置①时，左柱的最大塑性应变值发生在柱中部位（h=1.50m），达到0.2556，已超过材料的破坏失效应变（FS=0.2）；框架梁的最大塑性应变发生在梁左端，数值为0.1223。

表12 最大塑性应变（单位：×10-2）

图12给出爆炸源在最不利爆炸位置②（S=0.50m，HB=2.00m）时，框架结构的最终变形示意图。由图12不难看出，左柱最终水平位移的最大值发生在柱高h=2.00m处，右柱最终水平位移的最大值发生在柱顶（h=3.00m），两柱的最终竖向位移值很小。框架梁最终竖向位移的最大值发生在距梁左端x=0.50m处。

图12 结构最终变形（爆炸位置②）Fig.12 Final deformation of the structure（Explosive location②）

图13给出爆炸源在最不利爆炸位置②时，框架柱的最大水平位移和框架梁最大竖向位移响应的时程曲线，这些最大位移值Umax及其最终稳定值Ur 以及出现的时间T1和T2如表13所

图13 结构最大位移响应（爆炸位置②）Fig.13 Umax of the structure（Explosive location②）

表13 位移响应计算结果（爆炸位置②）

由图13和表13可以看出，最不利爆炸位置②情况下，左柱的水平位移响应与框架梁的竖向位移响应都比较大，左柱的水平位移响应最大值和最终值分别为75.05mm和68.42mm；框架梁的竖向位移响应最大值和最终值分别为51.82mm和42.28mm；右柱的水平位移响应相对较小，其最大值和最终值分别为23.61mm和12.05mm。左柱水平位移响应的最大值与最终值分别是右柱的3.18倍和5.68倍。

最不利爆炸位置②时，框架结构的塑性变形区如图14所示。由图14可以看出，框架结构的塑性变形主要集中在左柱上半部，左柱柱底以及框架梁左端。

图14 结构塑性变形区（爆炸位置②）Fig.14 Plastic deformation of the structure（explosive location②）

最不利爆炸位置②时结构的最大塑性应变值如表14所示。由表14可知，左柱的最大塑性应变值发生在爆炸源所在高度（h=2.00m）的腹板处，数值为0.2548，已超过材料的破坏失效应变；框架梁的最大塑性应变值为0.3653，发生在梁左端，也超过材料的破坏失效应变。

表14 最大塑性应变（单位：×10-2）

3 结论

本文对钢框架结构在内部爆炸荷载作用下的非线性动力响应进行了有限元分析。分析中考虑了爆炸源位置改变对结构动力响应的影响，从而确定了爆炸当量不变情况下使框架结构发生最大响应的爆炸源最不利位置。得到以下主要结论：

（1）爆炸源水平爆距的变化对框架柱动力响应影响较大，对框架梁的动力响应影响较小。随着水平爆距的减小，靠近爆炸源的框架柱的水平位移响应和塑性变形快速增长。结构的塑性变形主要集中在框架柱柱底和柱顶区域。

（2）爆炸源高度变化对框架梁动力响应的影响较大。随着爆炸源高度的提高，框架梁的竖向位移响应和塑性变形快速增长。爆炸源位于1/2柱高处框架柱的水平位移响应最大。结构的塑性变形主要集中在靠近爆炸源的框架梁端和梁的跨中。

（3）在本文考虑的爆炸源位置变化范围内，可以确定两个最不利爆炸位置。在这两个最不利爆炸位置，框架结构的动力响应相对较大，塑性区的最大塑性应变值超过材料的破坏失效应变。

[1] Nassr A A， Razaqpur A G， Tait M J. Experimental performance of steel beams under blast loading[J].Journal of Performance of Constructed Facilities， 2012，26（5）：600-619.

[2] Al-Thairy H. A modified single degree of freedom method for the analysis of building steel columns subjected to explosion induced blast load[J]. International Journal of Impact Engineering， 2016， 94：120-133.

[3] Oskouei A V， Kiakojouri F. Steel plates subjected to uniform blast loading[J]. Applied Mechanics & Materials，2011， 108: 35-40.

[4] Abdallah M， Osman B H. A methodology for evaluating dynamic responses of steel columns subjected to blast load under different situations[J]. Ies Journal Part A Civil& Structural Engineering，2015，8（4）：265-275.

[5] Zhai X， Wang Y. Modelling and dynamic response of steel reticulated shell under blast loading[J]. Shock &Vibration， 2013， 20（1）：19-28.

[6]丁阳， 汪明， 李忠献.爆炸荷载作用下钢框架结构连续倒塌分析 [J]. 建筑结构学报， 2012， 33（2）：78-84.

[7] Coffield A， Adeli H. Irregular steel building structures subjected to blast loading[J]. Journal of Civil Engineering& Management， 2016， 22（1）：17-25.

[8] Xiuhua Zhang， Zhongdong Duan， Chunwei Zhang.Numerical simulation of dynamic response and collapse for steel frame structures subjected to blast load[J].Transactions of Tianjin University， 2008， 14（1）:523-529.

[9]宋拓， 吕令毅. 爆炸冲击对多层钢框架连续倒塌性能的影响[J]. 东南大学学报（自然科学版）， 2011， 41（6）：1247-1252.

[10]张秀华， 吴燕燕， 李玉顺. 燃气爆炸作用下钢框架结构动力响应与连续倒塌分析[J]. 沈阳建筑大学学报（自然科学版）， 2012， 28（5）: 810-819.

[11] 李海旺， 薛飞， 秦冬祺. 爆炸荷载作用下平面钢框架变形形态研究[J]. 工程抗震与加固改造， 2005， 27（S1）: 155-161.

[12] Aubram， Daniel.Development and experimental validation of an arbitrary Lagrangian-Eulerian （ALE） method for soil mechanics[J]. Geotechnik， 2015， 38（3）：193-204.

[13]扈鹏.框架结构在爆炸冲击荷载下的动力响应及连续倒塌分析研究[D]. 西安: 长安大学， 2008.

[14] Dariani， B. M， Liaghat， et al. Experimental investigation of sheet metal formability under various strain rates[J].Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture， 2009， 223（223）：703-712.

[15]崔莹. 爆炸荷载下复式空心钢管混凝土柱的动态响应及损伤评估[D]. 西安: 长安大学， 2013.

Abstract：In this paper, the blast loading is simulated by use of ALE multi-material fluid-solid coupling method, and the whole process of dynamic response of single-span steel frame structures under internal blast loading is analyzed, the effect of the horizontal distance and the position height of the explosive on the structural response is investigated. The analysis results indicate that the horizontal explosive distance causes more affection on columns than the beam when the explosive height is lower, and the dynamic response of the beam increases with the raise of the explosive height when the explosive distance remains the same. Through analysis and comparison, most unfavorable locations of the explosive causing the maximum dynamic response of the frame structure are given.

Key words：blast loading；steel frame structure；nonlinear response

·简 讯 ·

Nonlinear Blast Response of Steel Frame Structures

WEI De-min, HUANG Qi-chao
（South China University of Technology, Guangdong Guangzhou 510640, China）

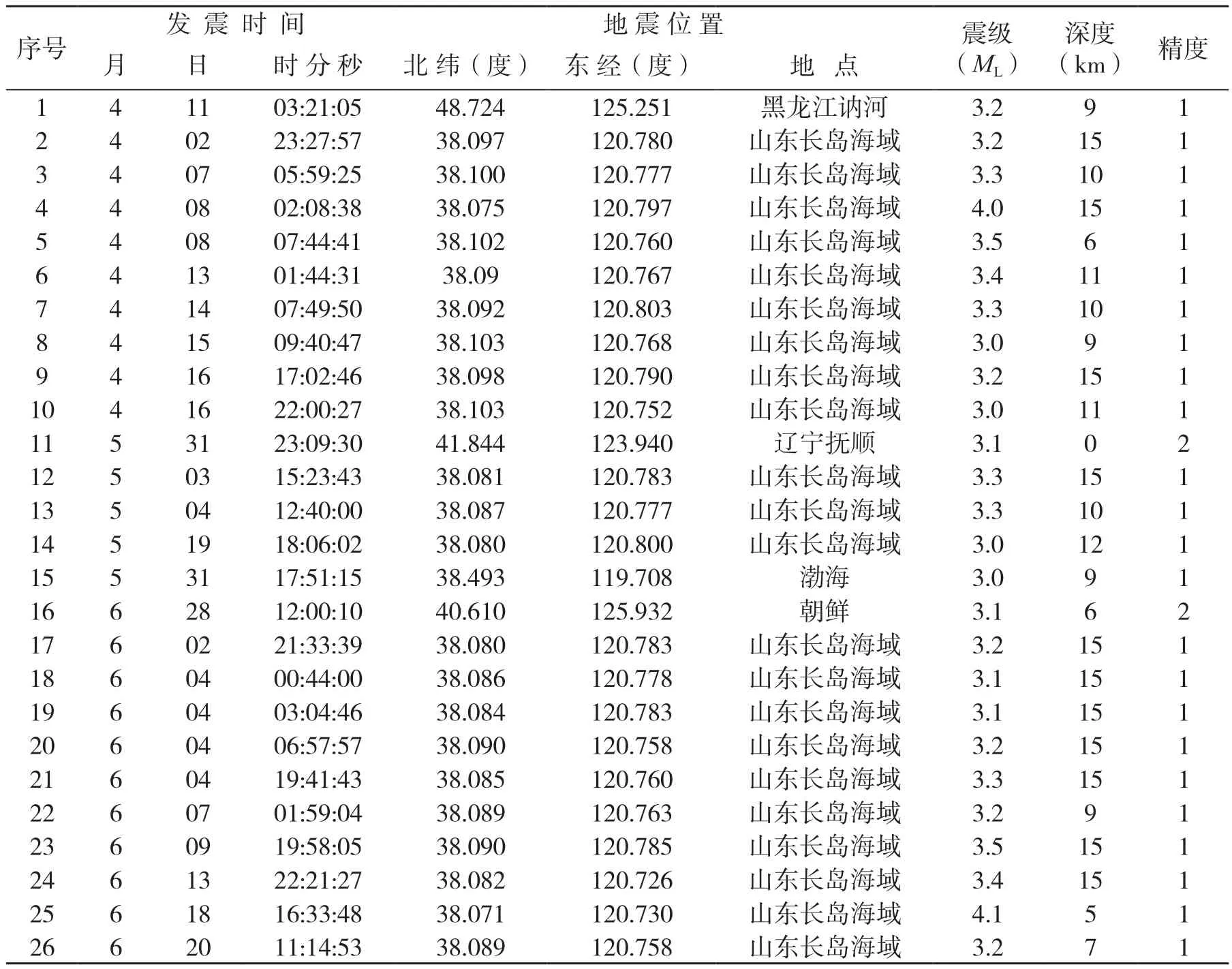
东北地区2017年第二季度ML≥3.0级地震目录The Earthquakes （ML≥3.0） Catalogue of the Second Quarter in Northeastern Area，2017

P315.9；TU375.4

A

10.13693/j.cnki.cn21-1573.2017.03.002

1674-8565（2017）03-0005-10

2017-04-12

2017-06-27

魏德敏（1955- ），女，四川省资中县人，2016年毕业于太原工业大学，固体力学专业，教授，博士生导师，现主要从事工程结构非线性动力响应、结构抗风、抗震等方面的研究工作。E-mail：dmwei@scut.edu.cn