注采比计算方法改进与应用
付 铭,刘德华,廖茂林
(长江大学 石油工程学院, 武汉 430100)
注采比计算方法改进与应用
付 铭,刘德华,廖茂林
(长江大学 石油工程学院, 武汉 430100)
注采比作为衡量注水过程注采平衡状态的一项重要参数,是反映产液量、注水量与地层压力之间联系的综合性指标。近年来我国多数注水油藏已进入开发后期,常规水驱特征曲线普遍存在上翘现象,因此传统方法计算误差往往较大。针对这一问题,应用油藏工程原理,结合高含水期水驱特征曲线推导出计算配水量新模型,该模型可有效地评价高含水期水驱开发效果。通过实例应用,与多元线性回归、BP神经网络法计算结果对比,可以看出该模型预测效果较好,可推广使用。
水驱油藏; 合理配水; 注采比
Abstract: Injection production ratio is an important parameter to measure the balance state of injection and production in the process of water injection, and it is a comprehensive index to reflect the relationship between liquid production, water injection and formation pressure. In recent years, most of the water flooding reservoirs in our country have entered the late stage of development. Therefore, the traditional water drive characteristic curve method often has a large error. In this paper, based on the principle of reservoir engineering, a new model of water distribution is deduced according to the characteristic curve of water drive. Through the application of examples, the improved multiple linear regression and BP neural network method are compared. The results show that the new method is better.
Keywords: water drive reservoir; reasonable water distribution; injection production ratio
注水作为油藏开发的主要方式,具有采收率高、容易控制与调整等优点。合理的配水量是稳定地层压力、提高采收率的重要保证。在油藏特高含水期,水驱自然递减率不断上升,产量递减快,确定合理的配产配注是解决问题的关键。调研结果表明:注采比计算方法主要有水驱特征曲线法、物质平衡法、logistic旋回法、存水率图版法、数值模拟法、多元线性回归法、BP神经网络法等。物质平衡法[1-2]将油藏看作封闭理想状态,但在开发后期油田存在外来水现象,只适合开发初期。数值模拟法[3-4]对油藏的动静态资料完善性要求较高,建模和历史拟合耗时周期长,不适合大型油田的开发指标预测。模型法[5-6]应用前提是参数B<0,只适用于采收率达到50%的递减阶段。存水率图版法[7-8]比较适合高采收率、存水率变化大的油藏。因此,本文借助于油藏工程原理,将水驱特征曲线与砂岩注采经验公式结合,建立符合特高含水期注采比计算模型。实际油藏计算结果表明:采用改进的方法计算注采比误差较小,符合油田开发要求。同时,针对文献[9-10]中多元线性回归法、BP神经网络法完善性提出改进意见,希望对油田采收率提高有所帮助。
1 注采比方法的改进
1.1 水驱特征曲线法
水驱特征曲线法原理是利用收集的油藏动态资料,将生产数据与水驱特征曲线拟合,得出拟合系数最高的水驱特征曲线表达式,代入对应的注采比表达式计算配水量。
陈元千[11]指出:甲型和乙型水驱曲线的直线段具有明显的平行特点。以甲型水驱特征为例,表达式为
logWp=a+bNp
(1)
式中:Wp为累计产水量(104t);Np为累计产油量(104t);a、b为甲型特征曲线截距与斜率,为常数。
杨国红等[12]给出符合甲型特征曲线注采比表达式:
logIPR=∂+log2.303β(1-fw)+
(2)
式中:IPR为注采比,无因次;fw为含水率,无因次; ∂、β为常数。
在油藏特高含水期[13],水驱特征容易出现上翘的现象,因此传统曲线计算误差较大。通过调研,特高含水期水驱特征曲线有二次型表达式[14]:
(3)
式中:WOR为水油比,无因次;A1、B1、C1为常数。
指数型表达式为[14]
logWOR=A2+B2Np+C2eNp
(4)
式中:A2、B2、C2为常数。
三次型水驱特征曲线表达式为[15]
(5)
式中:A3、B3、C3、D3为常数。
水油比定义式为
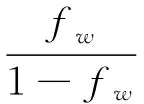
(6)
根据注水开发砂岩油藏注采经验关系式[16]
lg(Wi-F)=∂+βNp
(7)
式中:Wi为累计注水量(104t),可得注采比定义式:
IPR=Qi/Ql
(8)
式中:Ql为产液量(104t);Qi为注水量(104t)。
式(7)两边对t求导,得表达式
Qi/Qo=2.303β10∂+βNp
(9)
结合式(6)与式(3),得
(10)
结合式(8)~(10),得注采比表达式
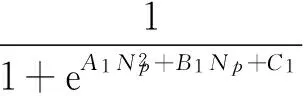
(11)
同理,可得指数型水驱特征曲线注采比表达式:
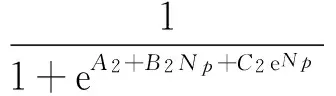
(12)
和三次型水驱特征曲线注采比表达式:
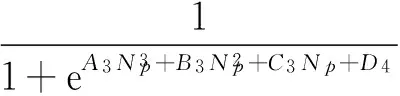
(13)
研究表明:通常情况下丁型水驱特征曲线[17]适合于低渗透低黏度(小于3 m·Pa·s)油藏,在我国特高含水期低渗透油藏一般采用CO2驱开采,所以丁型水驱特征曲线求解注采比模型意义不大。丙型特征曲线作为高含水期广泛应用的水驱曲线,表达式为[18]
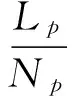
(14)
式中:Lp为产液量(104t);a3、b3为丙型特征曲线截距与斜率,为常数。
关恒[19]推导出丙型特征曲线含水率与累计产液量关系式
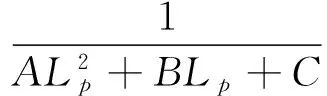
(15)

将式(15)代入式(9)中,得
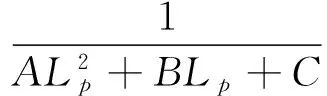
(16)
结合式(16)与式(14),得符合丙型特征曲线注采比表达式:
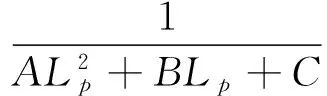
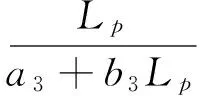
(17)
1.2 多元线性回归法
选取产液量、含水率、地层压力、累积注采比以及累积产液量等作为影响注采比的因子,得到注采比多元回归模型[9,20]:
IPR=b0+b1Ql+b2fw+b3P+
b4Lp+b5Z+ξ
(18)
式中:P为地层压力(MPa);Z为累计注采比,无因次;b0、b1、b2、b3、b4、b5为多元回归常数。
根据实际油藏n组生产数据,代入式(18)中,得矩阵形式
f·xi=yi
或
(19)
当误差ξ足够小时,存在无限接近于原函数的估算线性函数
(20)
为了得到观测值与估计值的误差平方和最小,根据最小二乘法的原理,得到误差平方和R2表达式
(21)
当R2取最小值时,可以得到最佳的多元回归模型。求解该模型主要有3种方法:
1) 打开Excel文件中Excel选项,“自定义功能区(B)”→勾取“开发工具”→“加载项”→勾取“分析工具库”→点“数据”中“数据分析”→“回归”。
2) 运用Matlab软件编写代码,[b,bint,r,rint,stats]=regress(Y,X,alpha)。bint是回归系数的区间估计,r是残差,rint是置信区间,stats是用于检验回归模型的统计量,alpha是显著性水平。
3) 打开“SPSS”导入相关数据,在窗口“分析”中点击“回归”,在“回归”子菜单中点击“线性”,在“线性回归”中导入应变量与自变量,点击“确定”可以得到多元线性回归结果。
1.3 BP神经网络法
神经网络预测法是根据BP神经网络结构[21-24],通过历史数据作为学习样本,在中间神经元传递函数推动下,通过不断调节网络的阈值与权值,让网络自动寻找内部表达形式。所以神经网络预测只能得到年产液量、综合含水率、总压差、累积产液量和累积注采比与IPR的非线性形式,无法得到具体的表达式。
1) 输入训练样本P,影响注采比的因素很多,通常选取年产液量、综合含水率、总压差、累积产液量和累积注采比5个因子作为输入层P。
3) 以sigmoid函数作为隐含层激励函数,根据具体情况选取适合的权值调整算法。
4) 确定训练步长为10 000,训练精度为0.0001。
神经网络预测注采比的代码程序:
>>clc
>>clear
>>P=[输入训练样本];
>>T=[输入样本目标值];
>>[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);
%创建网络
>>net=newff(minmax(p1),[5,9,1],{ ′tansig′,
′tansig′,′purelin′},′traingd′);
%设置训练次数
>>net.trainParam.epochs =10000;
>>net.trainParam.show=50;
%设置收敛误差
>>net.trainParam.goal=1e-4;
>>net.trainParam.lr =0.05;
%训练网络
>>[net,tr]=train(net,p1,t1);
>>a=[输入预测样本];
%将输入数据归一化
>>d=tramnmx(a,minp,maxp);
%放入网络输入数据
>>b=sim(net,d);
%将得到的数据反归一化得到预测结果
>>c=postmnmx(b,mint,maxt);c
2 实例应用
某注水开发砂岩油藏从1978年投入生产,初期主要依靠天然能量开采,中期地层能量亏空严重开始注水以提高地层能量,到2008年含水率达到90.34%。通过地质勘探得到油藏储量784.6×104t,束缚水饱和度为0.17,地层原油密度为0.91 t/m3,原油黏度8.5 m·Pa·s。油藏高含水期生产情况如图1所示。
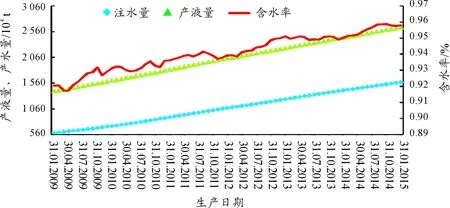
图1 油藏实际生产图
根据式(7),利用Excel中VBA编写程序对累计产油量与累计注水量进行线性差分拟合,得到表达式
lg(Wi+280.35)=1.693 5+0.004 6Np
(R2=0.999 9)
(22)
即 ∂=1.693 5,β=0.004 6。
由常规水驱特征曲线对油藏生产数据进行拟合,得到曲线系数及拟合系数,见表1,确定甲型与丙型最符合油藏开发特征。
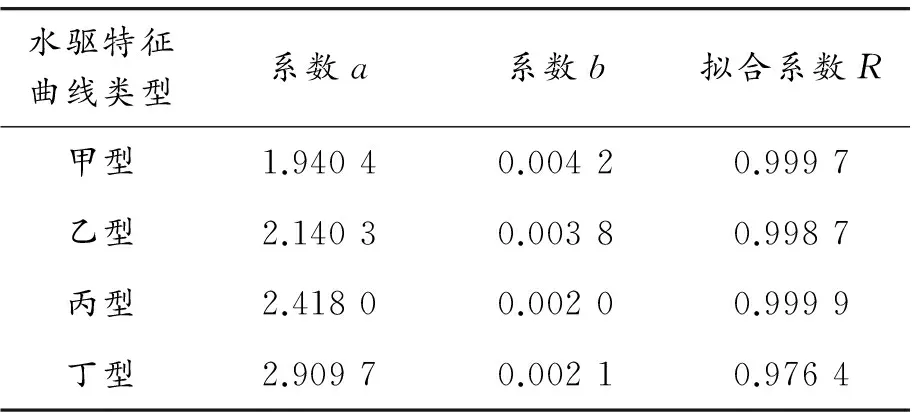
表1 4种水驱特征曲线与实际数据拟合的结果
根据特高含水期水驱特征曲线表达式,对实际生产数据拟合,通过图2可以确定该油藏最符合二次型水驱特征曲线。
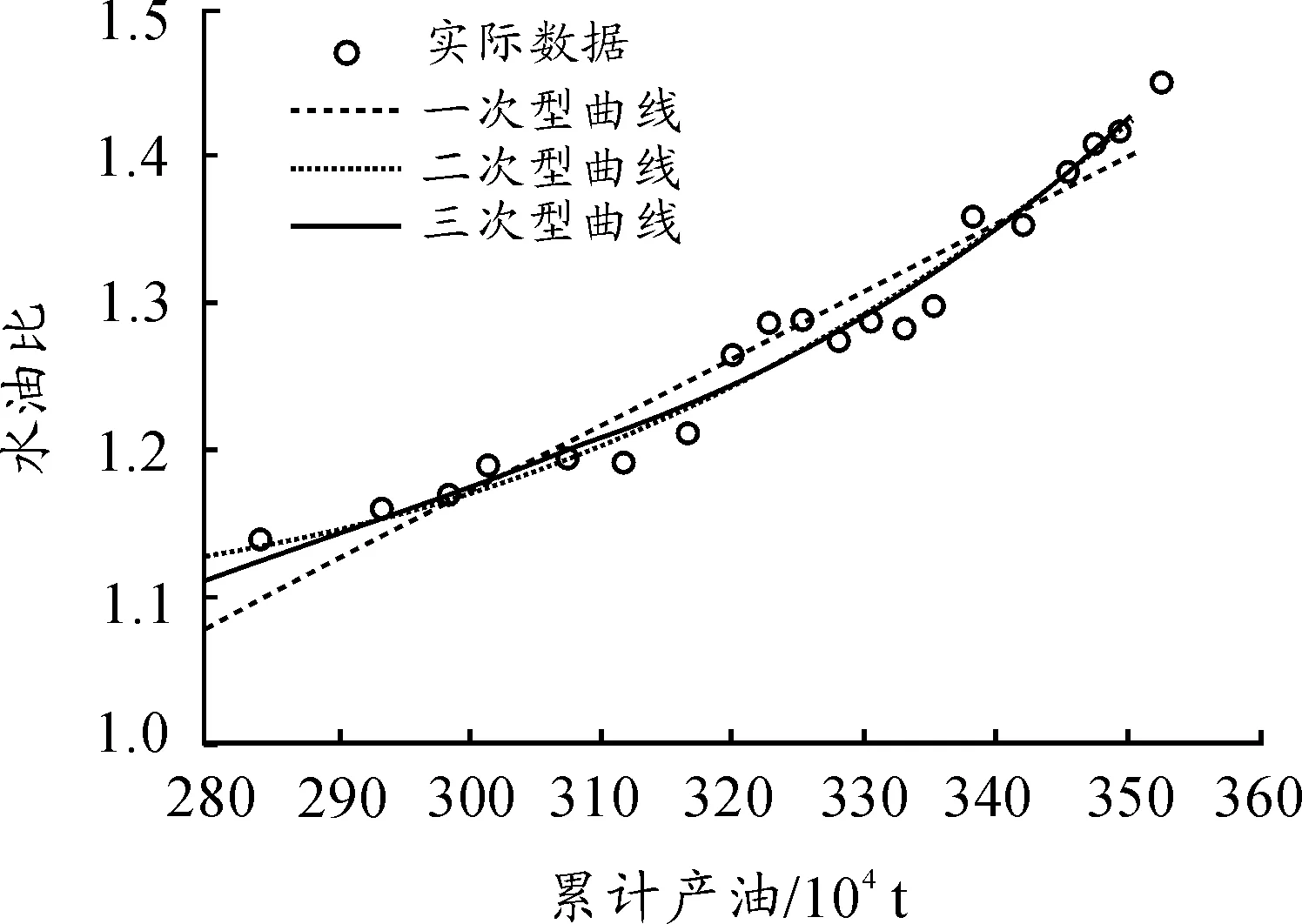
图2 特高含水期水驱特征曲线拟合
选取部分生产数据,由上述的丙型、甲型及新建的水驱特征曲线计算得注采比值与实际值误差,见图3。从图3中可见:随着含水率不断增高,改进的曲线计算精度更高。
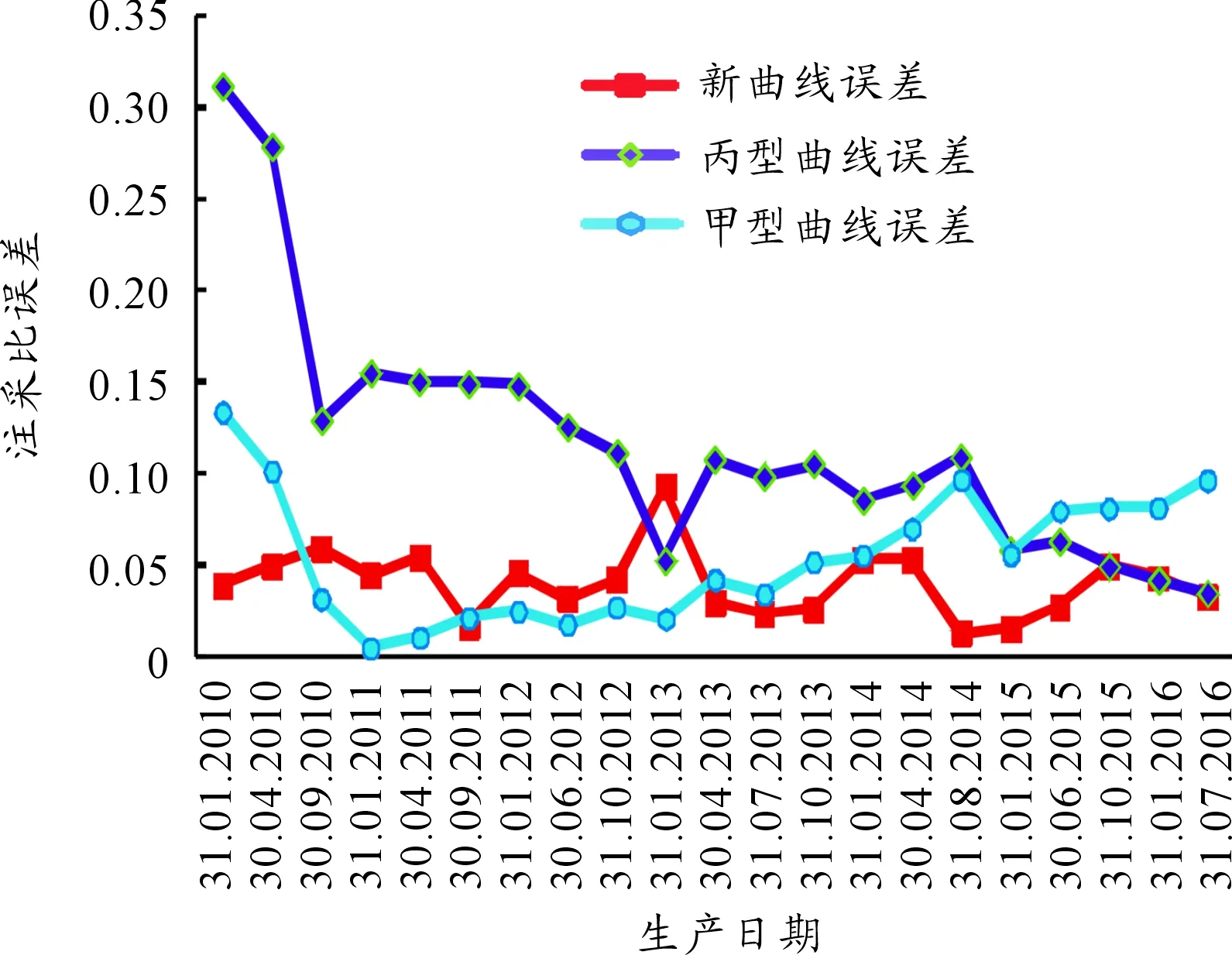
图3 几种曲线计算误差对比
由上述多元回归模型方法计算得图4。回归模型为
IPR=11.786 7+0.047 9Ql-13.195 8fw-
0.014 3P+0.000 153Lp+2.441 9Z
(23)
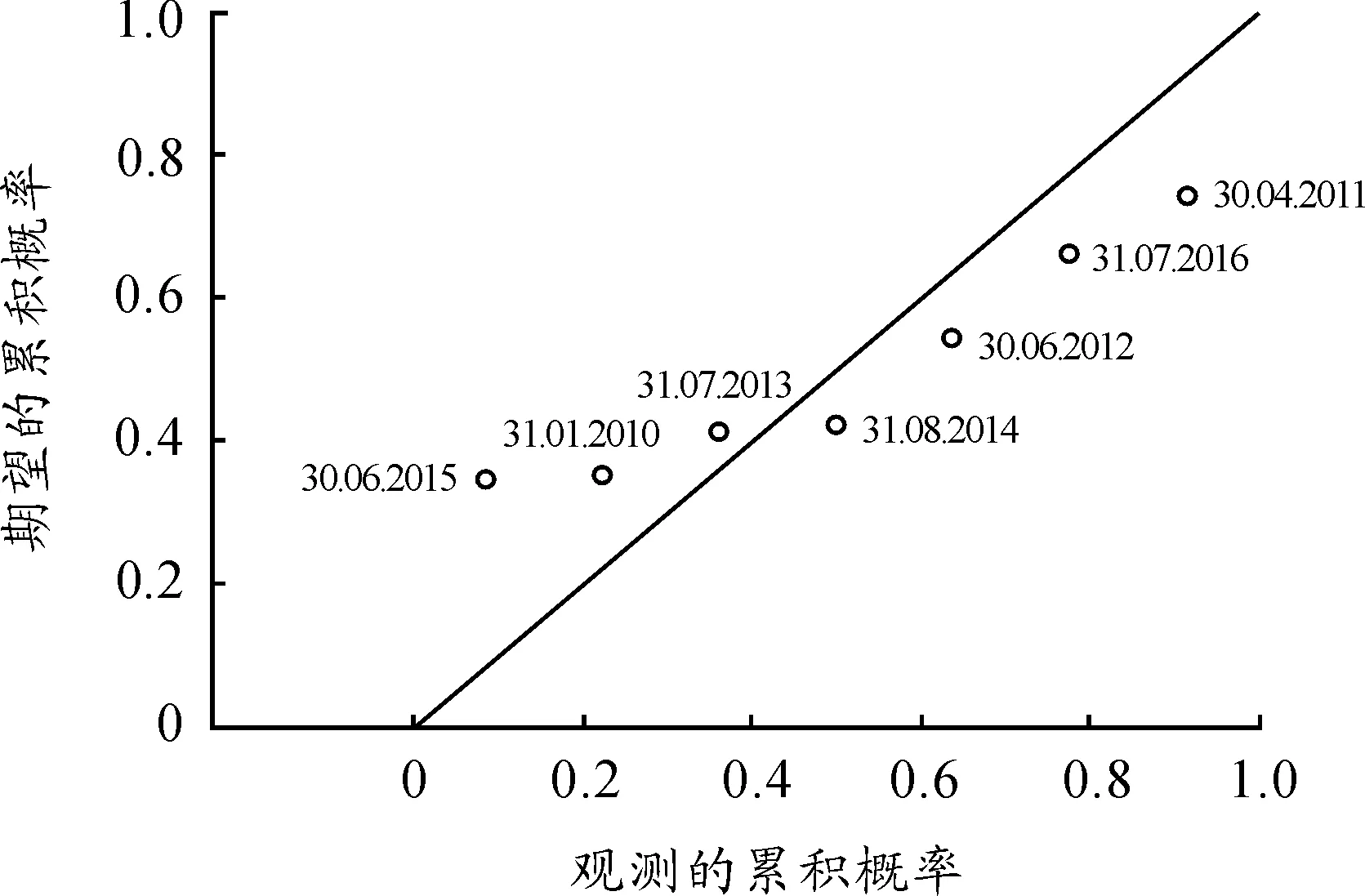
图4 回归标准化残差的标准P-P图
应用上述代码神经网络计算注采比代码,通过选取后期生产数据与多元回归法及水驱特征曲线法计算结果对比,结果如表2所示。
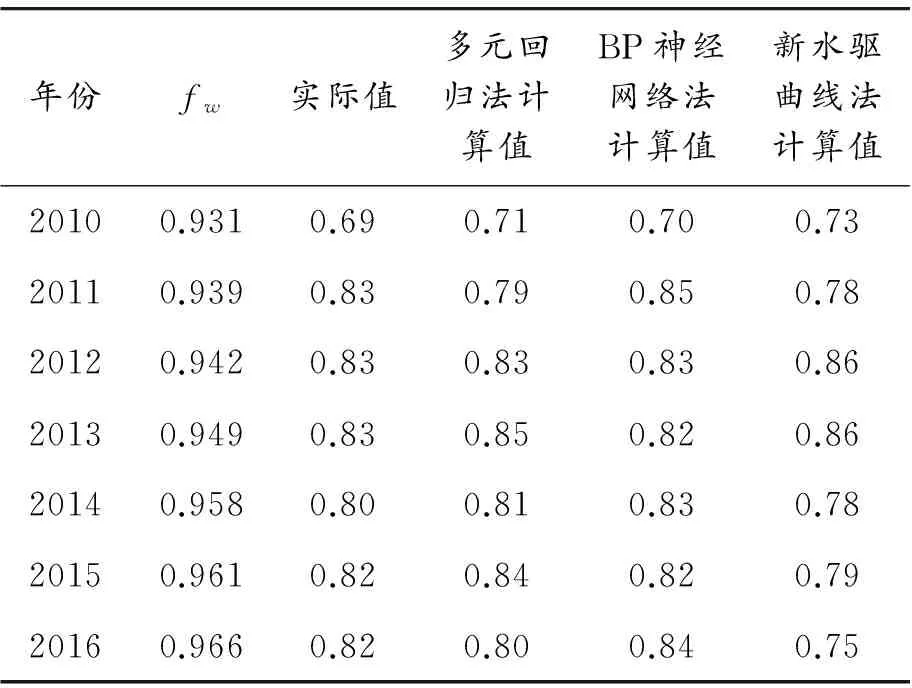
表2 BP神经网络法、多元回归法、新水驱曲线法得到的注采比对比
3 结束语
本文在总结前人研究成果的基础上,探讨了各种方法的优缺点。根据符合特高含水期水驱特征曲线,得到特高含水期注采比表达式,完善了注采比计算方法理论。
实际计算结果表明:改进的注采比计算方法更符合特高含水期精度要求。
注采比变化受储层结构、地层渗流特征等多种地质因素的影响,在实际应用中,应该对比各种方法计算。
与BP神经网络法和多元线性回归法相比,新水驱曲线法具有所需地质参数少、计算简单、精度高等优点,建议推广。
[1] 范姝.注采压力系统及合理注采比研究的一种方法[J].断块油气田,2009(5):72-74.
[2] 贾英兰,贾永禄,周霞,等.封闭油藏注水开发阶段注采比计算新方法[J].西南石油大学学报(自然科学版),2014(1):89-94.
[3] 曹勋臣,喻高明,邓亚,等.基于地层压力恢复时间的注采比数值模拟优化方法——以肯基亚克某亏空油藏为例[J].断块油气田,2016(2):193-196.
[4] 杨正明,曲海洋,何英,等.低渗透油藏分段压裂水平井井组周期注水数值模拟[J].科技导报,2015(22):69-72.
[5] 吴琼,张文忠,张春强.应用逻辑斯蒂旋回模型预测注水量的方法研究[J].特种油气藏,2011(1):67-69,138.
[6] 叶凡.利用Gompertz模型预测水驱油田合理注水量和注采比[J].重庆科技学院学报(自然科学版),2016(4):36-38.
[7] 张锐.应用存水率曲线评价油田注水效果[J].石油勘探与开发,1992(2):63-68.
[8] 黄李荣.注水开发油田单井配注方法研究[D].成都:西南石油大学,2006.
[9] 宫长路,田晓东,付百舟,等.多元回归方法在油田开发中的应用[J].大庆石油地质与开发,2006(4):65-67,123.
[10] 袁爱武,郑晓松.应用人工神经网络预测油田注采比[J].大庆石油地质与开发,2005(2):53-54.
[11] 陈元千.水驱曲线的典型图版及应用[J].新疆石油地质,1991(4):323-328.
[12] 杨国红,尚建林,王勇,等.水驱特征曲线注采比法优化配注计算[J].新疆石油地质,2013(1):59-62.
[13] 孙红霞.高含水期水驱特征曲线上翘新认识[J].特种油气藏,2016(1):92-95,155.
[14] 崔传智,徐建鹏,丁志莹,等.特高含水阶段水驱油藏开发指标计算方法研究[J].科学技术与工程,2016(4):22-27,53.
[15] 黄和钰,鞠斌山.基于对称变换的水驱特征曲线趋势分析方法[J].断块油气田,2017(1):35-39.
[16] 吴琼,韩玲,王玉英,等.新立油田注采比变化规律研究[J].特种油气藏,2013(3):68-71,154.
[17] 马艳丽,赵忠军,张振红,等.低渗低黏度油藏相渗曲线计算方法——丁型水驱特征曲线法[J].油气藏评价与开发,2012(6):28-31.
[18] 李正民,孙来喜,邓虎城等.水驱特征曲线的适用条件研究[J].物探化探计算技术,2012(2):143-146.
[19] 关恒.基于液油比的特高含水期水驱开发指标预测方法[J].岩性油气藏,2013(5):100-103.
[20] 袁迎中,张烈辉,何磊,等.注采比多元回归分析及合理注采比的确定[J].石油天然气学报,2008,30(1):299-302,398.
[21] 齐浩淳,黄大鹏,魏久南,等.基于BP神经网络的高寒山地弹药消耗需求分析[J].兵器装备工程学报,2016,37(6):97-101.
[22] 郑永,陈艳.基于BP神经网络的高校教师教学质量评价模型[J].重庆理工大学学报(自然科学),2015,29(1):85-90.
[23] 田增山,崔永全.基于BP神经网络的GPS/SINS姿态测量融合算法[J].重庆邮电大学学报(自然科学版),2014,26(4):478-482.
[24] 陈雯柏.人工神经网络原理与实践[M].西安:西安电子科技大学出版社,2016.
(责任编辑杨黎丽)
ImprovementandApplicationofInjectionProductionRatioCalculationMethod
FU Ming, LIU Dehua, LIAO Maolin
(School of Petroleum Engineering,Yangtze University, Wuhan 430100, China)
2017-06-28
国家自然科学基金资助项目(41302119)
付铭(1992—) 男,湖北黄冈人,硕士研究生,主要从事油气数值模拟研究,E-mail:mingtangtangzhu@163.com; 通迅作者 廖茂林(1991—),男,湖北武汉人,硕士研究生,主要从事油气田开发、油藏井间性以及提高采收率研究,E-mail:m18062792757@163.com。
付铭,刘德华,廖茂林.注采比计算方法改进与应用[J].重庆理工大学学报(自然科学),2017(9):97-102.
formatFU Ming, LIU Dehua, LIAO Maolin.Improvement and Application of Injection Production Ratio Calculation Method[J].Journal of Chongqing University of Technology(Natural Science),2017(9):97-102.
10.3969/j.issn.1674-8425(z).2017.09.016
TE357
A
1674-8425(2017)09-0097-06

