矩阵相抵分解的若干结论

戴立辉，吴霖芳

（闽江学院，福建 福州 350108）

矩阵相抵分解的若干结论

戴立辉，吴霖芳

（闽江学院，福建 福州 350108）

矩阵相抵分解是一类特殊的矩阵分解问题，它在解决矩阵的秩、标准形化简等许多问题中都有重要的应用。通过对矩阵分解的深入探讨，得到一系列相关结论，对矩阵的进一步研究具有重要的理论意义。

矩阵；相抵；相抵分解；结论

0 引言

矩阵分解问题是线性代数内容之一，具有丰富的理论内涵与广泛的应用价值，在矩阵理论及应用中起着重要的作用。矩阵相抵分解就是一类特殊的矩阵分解问题，它在解决矩阵的秩、逆矩阵、行列式、标准形化简等许多问题中都有重要的应用。

关于矩阵的相抵分解，其基本内容在文献[1-4]中都有涉及。林亚南在文献[5]中从矩阵的相抵谈起，进一步讨论了矩阵的相抵分解，得到一些结果；朱荣坤在文献[6]中结合考研试题，研究了矩阵的相抵标准形，得到一些考研试题的相抵标准形的证法。

本文通过系统、深入探讨矩阵相抵分解的本质，得到一系列相关结论，可作为文献[1-6]的补充或提高，对矩阵的进一步研究具有重要的理论意义。

本文中，Fm×n表示数域F上m×n矩阵的全体，Er表示r阶单位矩阵，r（A）表示矩阵A的秩，A-1表示矩阵A的逆矩阵，AT表示矩阵A的转置。

1 预备知识

定义1 设矩阵A通过一系列初等变换得到矩阵B，则称A和B相抵。

引理1 设矩阵A与B相抵，则以下表述等价：

（1）A可以通过有限次行和列的初等变换最终得到B；

（2）设 A ∈ Fm×n，则存在初等矩阵 P1，P2，…，Ps，Q1，Q2，…，Qt使得

（3）存在可逆矩阵 P ∈ F×，Q ∈ F×，使得A=PBQ；

（4）A，B可分别通过有限次行和列的初等变换最终得到同一个

（5）（rA）=（rB）。

引理2 设 A ∈ Fm×n，r（A）=r，则存在可逆矩阵P ∈ Fm×m，Q ∈ Fn×n，使得

2 主要结论

定理1设A ∈ Fn×n，（rA）=r，则

（1）存在可逆矩阵 P ∈ Fn×n，使得PAP-1后n-r行全部为零；

（2）存在可逆矩阵 Q ∈ Fn×n，使得Q-1AQ后n-r列全部为零。

证明 （1）存在可逆矩阵P，Q ∈ Fn×n，使得则PAP−1=PAQQ−1P−1=

（2）同（1）可证。

定理2设A ∈ Fn×n，（rA）=r，则

（1）存在可逆矩阵 P ∈ Fn×n，使得

（2）存在可逆矩阵 Q ∈ Fn×n，使得

证明 （1）存在可逆矩阵P， Q ∈ Fn×n，使得则令

其中A ∈Fr×n，且 （rA1）=r。

1

（2）同（1）可证。

由定理2可知，A相似于

定理3 设 A ∈ Fn×n， r( A) =r，则存在 B , C ∈ Fn×n，使得AB=CA=A，其中 （rB）=（rC）=r。或A相似于

证明 存在可逆矩阵P，Q ∈ Fn×n，使得则 （rB）=（rC）=r，且AB=CA=A。

定理4设A ∈ Fn×n，（rA）=r，则

（1）存在幂等矩阵 B ∈ Fn×n和可逆矩阵 C ∈ Fn×n，使得A=BC；

（2）存在可逆矩阵D ∈ Fn×n和幂等矩阵 H ∈ Fn×n，使得A=DH。

证明 （1）存在可逆矩阵 P , Q ∈ Fn×n，使得则

令则B2=B，C可逆，使得A=BC。

（2）同（1）可证。

由定理可知，n阶方阵可经过有限次行的（或列的）初等变换化为幂等矩阵。

定理5设A ∈ Fn×n，（rA）=r，则

（1）存在对称矩阵 B ∈ Fn×n和 可逆矩阵 C ∈ Fn×n，使A=BC；

（2）存在可逆矩阵 D ∈ Fn×n和 对称矩阵 H ∈ Fn×，n使A=DH。

证明 （1）存在可逆矩阵 P , Q ∈ Fn×n，使得则

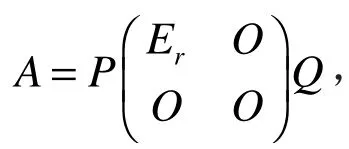
令则BT=B,C可逆，使得A=BC。

（2）同（1）可证。

定理5说明，n阶方阵可经过有限次行的（或列的）初等变换化为对称矩阵。

定理6 设 A ∈ Fn×n， r( A) =r < n， 则

（1）存在B≠O，（rB）=n-r，使得AB=O；

（2）存在B≠O，（rB）=n-r，使得BA=O；

（3）存在B≠O，（rB）=n-r，使得AB=BA=O。

证明 存在可逆矩阵P，Q ∈ Fn×n，使得

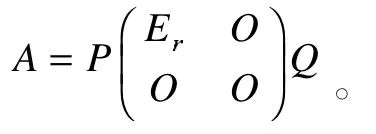
（1）令则 B≠O，r（B）=n-r，且AB=O；

（2）令则 B≠O，r（B）=n-r，且BA=O；

（3）令则B≠O，r（B）=nr，且 AB=BA=O。

定理7 设 A , B ∈ Fn×n，且则存在可逆矩阵 M ∈ Fn×n，使得AMB=O。

令 M=Q-1R-1，则 AMB=O。

定理8设A ∈ Fm×n，（rA）=r，则存在A1，A2，…，Ar∈ Fm×n，使得

A=A1+A2+…+Ar，其中 （rA）i=1（i=1，2，…，r）。

证明 存在可逆矩阵 P ∈ Fm×m，Q ∈ Fn×n，使得则

其中Eij表示第i行、第j列元素为1，其他为0的矩阵。

令Ai=PEiiQ（i=1，2，…，r），则r（A）i=1（1，2，…，r），且

定理9设A ∈ Fm×n，（rA）=r则

（1）存在可逆矩阵 P ∈ Fm×m，使得

（2）存在可逆矩阵 Q ∈ Fn×n，使得

A = (N, O) Q ，其中 N ∈ Fn×r，且 r ( N)=r 。

证明 （1）存在可逆矩阵 P ∈ Fm×m， Q ∈ Fn×，n使得令其中 M ∈ Fr×n，于是

（2）同（1）可证。

定理10 设 A ∈ Fm×n， r ( A)=r ， 则存在 M ∈ Fm×r，N ∈ Fr×n使得A=MN，其中 r ( M ) = r ( N ) =r 。

证明 存在可逆矩阵 P ∈ Fm×m， Q ∈ Fn×n，使得故

其中且r（M）=r（N）=r。

定理10中的分解称为矩阵的满秩分解。

定理11 设 A ∈ Fm×n，

（1）若 （rA）=n，则存在可逆矩阵P ∈ Fm×m，使得

（2）若 （rA）=m，则存在n阶可逆矩阵Q ∈ Fn×n，使得 A = (Em,O) Q 。

（2）因为 （rA）=m，所以 （rAT）=m

由（1）存在可逆矩阵 P ∈ Fm×m，使得故A = (Em,O) PT，令 Q=PT，则 A=(Em，O)Q。

定理11中的分解称为矩阵的行（或列）满秩分解。

定理12 设 A ∈ Fm×n，

（1）若 r（A）=n，则存在 B ∈ Fn×m，使得 BA=En，ABA=A；

（2）若 r（A）=m，则存在 C ∈ Fn×m，使得 AC=Em，CAC=C。

证明 （1）存在可逆矩阵 P ∈ Fm×m， Q ∈ Fn×n，使得令 B = (Q−1, O) P−1，则

BA=En。从而 ABA=A。

（2）同（1）可证。

定理13 设 A ∈ Fm×n， r( A) =r 则存在 B ∈ Fn×m，使得 ABA=A，BAB=B。

证明 存在可逆矩阵 P ∈ Fm×m，Q ∈ Fn×n，使得令可得 ABA=A，BAB=B。

［1］北京大学数学系几何与代数教研室前代数小组.高等代数（第三版）［M］.北京：高等教育出版社，2003.

［2］林亚南.高等代数［M］.北京：高等教育出版社，2013.

［3］庄瓦金.高等代数教程［M］.北京：科学出版社，2013.

［4］辛林，周德旭.高等代数［M］.杭州：浙江大学出版社，2012.

［5］林亚南.从矩阵的相抵谈起［A］.福建省《高等代数》与《线性代数》课程建设第十次研究讨会交流论文，2008.

［6］朱荣坤.矩阵相抵标准形的考研试题研究［A］.福建省《高等代数》与《线性代数》课程建设第十五次研究讨会交流论文，2013.

A Series of Conclusions of Matrix Counterbalance Decomposition

DAI Li-hui，WU Lin-fang
(Minjiang University，Fuzhou 350108，China）

Matrix counterbalance decomposition,one of the special matrix decomposition issues,plays a major role in solving many problems such as the rank of the matrix and standard form reduction.Based on the further discussion about matrix decomposition,the paper draws a series ofrelevant conclusions in hope that it lays an important theoretical significance on the matrixresearch.

matrix；counterbalance；counterbalance decomposition；conclusion

O151.2

A

1674-3229（2017）03-0012-03

2017-03-16

戴立辉（1963-），男，闽江学院数学系教授，研究方向：矩阵论。