开关电感Buck-Boost变换器的非线性行为控制研究

王礼辉，陶彩霞，田莉

（兰州交通大学自动化与电气工程学院，甘肃 兰州 730070）

开关电感Buck-Boost变换器的非线性行为控制研究

王礼辉，陶彩霞，田莉

（兰州交通大学自动化与电气工程学院，甘肃 兰州 730070）

以电流模式控制开关电感Buck-Boost变换器为研究对象，通过数值仿真得到了电路系统的分岔图、庞加莱截面图、最大Lyapunov指数、雅可比矩阵特征值，分析了变换器电路系统非线性行为及混沌产生的原因，推导出了电路系统的稳定判据。首次采用参数微扰法对开关电感Buck-Boost变换器的非线性行为进行了控制，并计算了扰动强度和扰动相位。最后进行了相应的Matlab/Simulink仿真和实验电路验证，实验结果与仿真结果一致。研究结果表明，采用参数微扰法可有效抑制电路系统的混沌。

开关电感Buck-Boost变换器；数值仿真；非线性行为；参数微扰法；控制

Abstract:The current-mode controlled switched-inductor Buck-Boost converter was chosen as the research object.Through numerical simulation，the bifurcation diagram，the Poincare section diagram，the largest Lyapunov exponent and the Jacobian matrix eigenvalue of this circuit system were shown here.The switched-inductor Buck-Boost converter circuit system nonlinear behavior and the case of chaos were analyzed，and stability criterion of circuit system was deduced.For the first time，the parametric perturbation method was applied to control the nonlinear behavior in switched-inductor Buck-Boost converter.At the same time，pertubation amplitude and pertubation phase angle were calculated.Finally，the corresponding Matlab/Simulink simulation and experimental circuit validation were done.The result shows that the chaos of the circuit system can be reduced efficiently by the parametric perturbation method.

Key words:switched-inductor Buck-Boost converter；numerical simulation；nonlinear behavior；parametric perturbation method；control

开关DC-DC变换器是开关电源的核心组成部分，属于非线性时变离散动力学系统，会产生各种类型的分岔、混沌等非线性物理现象［1］。随着对电路系统混沌及分岔研究的重视，已对多种类型的电力电子变换器非线性行为进行了深入研究［2-10］。为提高变换器系统的性能，同时也研究了其非线性行为控制方法［11-13］。已有的混沌、分岔控制方法总体上可分为反馈控制法和非反馈控制法，其中参数微扰法属于非反馈控制法，由于其易于实现而得到了广泛应用，因此有必要对其进行深入研究。开关电感结构是近年来提出的一种新型拓扑，可嵌入到传统DC-DC变换器中，用来提高系统的升降压能力。目前对开关电感DC-DC变换器非线性现象的研究仍属起步阶段，文献［14-15］研究了开关电感Boost，Buck-Boost变换器的混沌、分岔行为，然而，对开关电感型变换器非线性现象控制方法的研究却尚未开展。

文章对基于参数微扰法的电流模式开关电感Buck-Boost变换器混沌的控制进行了研究，推导出了电路系统的稳定判据，对扰动强度及扰动相位的选取进行了理论分析，并对电路系统进行了Matlab/Simulink仿真和验证。研究结果表明，加入合适的扰动后，电路系统可由混沌控制到1周期状态。本研究成果可有效地应用在新能源光伏发电、轨道交通装备、电动汽车控制等领域中，对抑制开关变换器的混沌，改善系统的稳定性和降低系统的EMI，都具有重要的意义。

1 电路系统非线性行为

1.1 电路系统工作原理

电流模式控制开关电感Buck-Boost变换器电路原理图如图1所示，虚线框内为开关电感结构。电路工作原理如下：将电感L1的电流iL1与参考电流Iref比较的结果作为RS触发器R端的输入，时钟信号通过触发器的S端输入，触发器的Q端控制开关管S的通断。

图1 电流模式控制开关电感Buck-Boost变换器Fig.1 Current-mode controlled switchedinductor Buck-Boost converter

开关电感Buck-Boost变换器工作在断续导通模式时，电路有3种模态，如图2所示。

图2 断续导通运行时的模态Fig.2 Discontinuous conduct mode

为便于分析，令L1=L2，则电感电流和近似相等，因而系统可简化为二阶模型［10］，其状态方程如下式：

式中：x为状态变量，即；U为输入电压；A，B分别为系数矩阵。

根据式（1），采用频闪映射方法，对状态变量离散化可得到断续导通模式时开关电感Buck-Boost变换器的离散时间映射模型，见文献［15］。由离散时间映射模型，通过数值仿真可对系统的非线性行为进行分析。电路参数为：U=6 V，R=10 Ω，C=10 μF，L1=L2=100 μH，T=100 μs，Iref= 1～20A。

1.2 分岔图

图3为以参考电流为分岔参数时由数值仿真得到的电感电流分岔图和电容电压分岔图，随着参数的变化，分岔图可以清晰地展示出电路系统的非线性行为变化情况。根据图3可知，在参考电流增大的过程中，由于分岔的发生，其中分岔主要有倍周期分岔及边界碰撞分岔，系统在周期状态和混沌之间交替变化，具有复杂的非线性行为。

图3 参考电流为分岔参数的分岔图Fig.3 The bifurcation diagrams with the refreence current as a bifurcation parameter

1.3 庞加莱截面图

由数值仿真得到的以参考电流为变化参数时不同取值情况下的庞加莱截面图如图4所示。庞加莱截面图是研究非线性系统动力学行为的常用工具，系统所处的状态可根据庞加莱截面图上不同特征的几何图形确定。由图4可知，在不同的参考电流取值下，系统处于周期状态时庞加莱截面图由有限的离散点组成；系统处于混沌时庞加莱截面图为沿线段或曲线弧分布的点集。

图4 不同参考电流下的庞加莱截面图Fig.4 The poincare setion diagrams with the different refreence current

1.4 最大Lyapunov指数

最大Lyapunov指数是判断非线性系统是否出现混沌的一种重要方法，当系统的最大Lyapunov指数小于零时，系统为周期状态；反之，则为混沌。由仿真得到的以参考电流为变化参数的最大Lyapunov指数谱如图5所示，仿真结果与图3相对应，证明了系统离散时间映射模型的正确性。

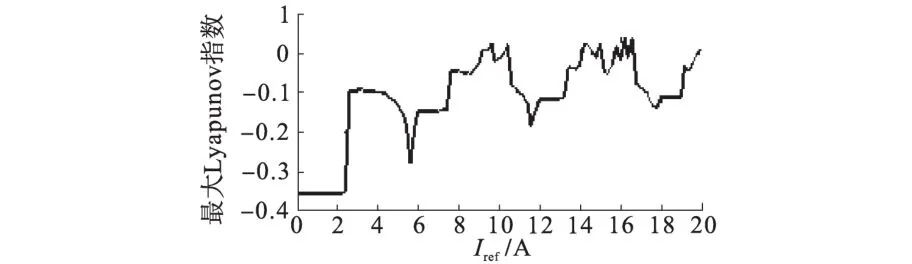
图5 最大Lyapunov指数谱Fig.5 The largest Lyapunov exponent spectrum

1.5 雅可比矩阵特征值

根据系统离散时间映射模型在不动点邻域处的雅可比矩阵特征值可确定系统的工作状态。图6为以参考电流为变化参数由仿真得到的雅可比矩阵特征值的轨迹变化，若两特征值在单位圆内，则系统为周期状态；若有1个特征值在圆外，则系统为混沌。其中，参考电流为8 A，9.5 A，12.5 A时系统的雅可比矩阵特征值如表1所示。仿真结果与图4相对应，进一步证明了系统离散时间映射模型的正确性。

图6 雅可比矩阵特征值轨迹Fig.6 The Jacobian matrix eigenvalue loci

表1 不同参考电流时的特征值Tab.1 The Jacobian matrix eigenvalue with the different refreence current

2 非线性行为控制—参数微扰法

2.1 电路系统的稳定判据

由以上数值仿真的结果可知，随着参考电流的增大，电路由稳态进入到分岔再到混沌状态最后在分岔和混沌之间往复变化，电路系统状态发生了失稳，电路失稳分析及稳定判据推导如下。

构造关于电感电流和占空比的离散映射函数为

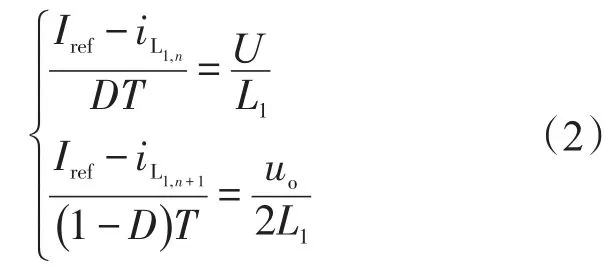
式中：D为占空比，即开关周期中开关管导通时间所占比例；uo为输出电压；分别为开关周期开始和结束时刻的电感电流。

由式（3），方程的特征值λ为

根据非线性动力学理论，系统工作在稳定的1周期状态时，则D的取值范围为（0，0.5），由此若D的取值不在稳态范围内，则系统会出现混沌、分岔等不稳定现象。由功率平衡法则有

式中：Δi为电感电流波动幅度，。

则以参考电流为分岔参数时的稳定判据为

电感电流断续时，考虑到时间常数、开关周期等因素，令其稳态输出电压，则稳定判据为

2.2 参数微扰法的微小扰动计算

参数微扰法利用混沌状态对参数微小扰动极为敏感的特性，通过给参数施加一定的微小扰动可将系统从混沌状态控制到稳定的1周期状态。通常在对电路系统影响较大、易于改变的参数中加入微小扰动，如选择参数C，用C*=C+Asin（2πft+φ）来代替C。在电流模式控制开关电感Buck-Boost变换器中可加入扰动的参数有很多，如电源U、负载电阻R、电容C、参考电流Iref等，其中Iref是较易改变的参数，因此可在参考电流中加入小扰动，即，其中的扰动频率f通常取为系统的开关频率，扰动强度A及扰动相位φ的计算如下：

构造加入扰动后关于电感电流和占空比的离散映射函数，即

同样考虑系统稳态时，令

则式（8）的摄动小量形式为

式（10）的特征值λ为

当λ=-1时，临界占空比，由此可知加入扰动后系统的稳态占空比范围变大。因而参数微扰法可以抑制系统混沌现象，提高系统稳定性。将临界占空比代入式（7），参考电流取其临界值，则有

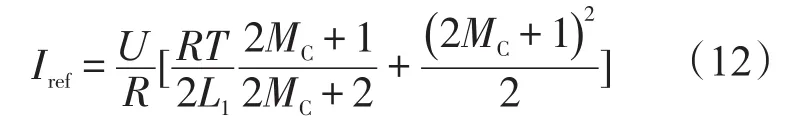
当MC取最大值时，则临界占空比DL取得最大值，依据式（11），取MC的最大模值为其最大值，由MC=L1mC/U可知：

则由式（13）和式（14）可得到扰动相位和扰动强度。

3 仿真和实验验证

3.1 仿真验证

根据上述仿真结果可知参考电流Iref=9.5 A时电路系统处于混沌，以此为例，采用参数微扰法对开关电感Buck-Boost变换器的混沌进行控制。由前面的分析可知，扰动频率为系统的开关频率f=104Hz，扰动相位及扰动强度分别为φ= 4.02 rad和A=2.54。由扰动参数和1.1中的电路参数，可在Matlab/Simulink中进行电路仿真，在4 ms时刻加入小扰动。

图7为加入小扰动前后由仿真得到的电容电压和电感电流的时域波形图和相轨图。

图7 仿真时域波形图及相图Fig.7 The simulation time domain waveforms and phase diagrams

由仿真结果可知，加入扰动前的波形处于混沌往复无周期、无规律，加入扰动之后经过短暂的过渡，波形趋于1周期稳定状态，并且使得开关电感Buck-Boost变换器的运行模式发生了转移。使其由电感电流断续模式转移到电感电流连续模式。由此可知，参数微扰法对开关电感Buck-Boost变换器的混沌有较好的抑制作用，提高了变换器的性能，与前述理论分析相一致。

3.2 实验验证

根据图1搭建实验电路验证参数微扰法对系统的非线性行为控制作用，实验电路参数选取与仿真参数的设置一致，其中开关管选取为IRFZ34型MOSFET开关管，二极管为FR307型快恢复二极管，供电电源选择为SS3323型可跟踪直流稳压电源；控制电路中选取电感电流为反馈量，由LT1357型运算放大器将采样电阻两端电压放大后作为电感电流的采样信号，采样信号与参考电流和外加小扰动电流之和相比较可控制RS触发器，最终控制MOSFET开关管的导通。

加入小扰动电流前后的实验结果如图8所示。由图8可知，当采用参数微扰法控制电路系统非线性行为时的实验结果与Matlab/Simulink仿真结果一致，验证了理论分析的正确性和参数微扰法对非线性行为控制的有效性。

图8 实验时域波形图及相图Fig.8 The experiment time domain waveforms and phase diagram

4 结论

本文首次采用参数微扰法对开关电感Buck-Boost变换器的混沌进行控制，通过理论分析和仿真及实验验证，研究结果表明参数微扰法可以对电流模式控制开关电感Buck-Boost变换器的混沌进行有效控制，在扰动选取合适的情况下，可以使电路系统稳定工作在1周期状态，并计算了扰动强度和扰动相位，推导出了基于参考电流的电路系统稳定判据。可为后续开关电感Buck-Boost变化器的混沌控制方法研究及其实际工程应用提供重要指导作用。

［1］包伯成.混沌电路导论［M］.北京：科学出版社，2013.

［2］杨平，许建平，何圣仲，等.电流控制二次型Boost变换器的动力学研究［J］.物理学报，2013，62（16）：45-52.

［3］潘赛虎，曹秋娟，史国栋，等.电流控制反激式变换器动力学特性研究［J］.电测与仪表，2015，52（3）：64-69.

［4］柴玉华，孙影，刘洪臣，等.基于随机扩频的Boost变换器非线性现象的研究［J］.电测与仪表，2013，50（3）：81-85.

［5］谢玲玲，龚仁喜，卓浩泽，等.电压模式控制不连续传导模式Boost变换器切分岔研究［J］.物理学报，2012，61（5）：479-485.

［6］Deivasundari P S，Uma G，Poovizhi R.Analysis and Experi⁃mental Verification of Hopf Bifurcation in a Solar Photovoltaic Powered Hysteresis Current-controlled Cascaded-Boost Con⁃verter［J］.Institution of Engineering and Technology Power Electronics，2013，6（4）：763-773.

［7］Aroudi E A，Rodriguz E，Leyva R，et al.A Design Oriented Combined Approach for Bifurcation Prediction in Switchedmode Power Converters［J］.IEEE Transactions on Circuits and Systems II：Express Briefs，2010，57（3）：218-222.

［8］Mandalk K，Banerjee S，Aborty C.Symmerty-breaking Bifurca⁃tion in Series-parallel Load Resonant DC-DC Converter［J］. IEEE Transactions on Circuits and Systems I：Regular Papers，2013，60（3）：778-787.

［9］Singha A K，Kapat S，Banerjee S.Nonlinear Analysis of Dis⁃cretization Effects in a Digital Current Mode Conrolled Boost Converter［J］.IEEE Jouranl on Emerging and Selected Top⁃ics in Circuits and Systems，2015，5（3）：336-344.

［10］Basak B，Parui S.Exploration of Bifurcation and Chaos in Buck Converter Supplied From a Rectifier［J］.IEEE Transac⁃tion on Power Electronics，2010，25（6）：1556-1564.

［11］杨平，包伯成，沙金，等.开关变换器斜坡补偿动力学机理研究［J］.物理学报，2013，62（1）：57-65.

［12］李冠林，李春阳，陈希有，等.基于共振参数微扰法的SEPIC变换器的混沌控制［J］.物理学报，2013，62（21）：71-78.

［13］郑连清，申滔，池俊峰.断续导通模式下Buck变换器的混沌分析及其滑模控制［J］.电力自动化设备，2012，32（7）：30-35.

［14］刘洪臣，杨爽，王国立，等.基于开关电感结构的混合升压变换器非线性现象研究［J］.物理学报，2013，62（15）：66-73.

［15］孙立山，杨爽，刘洪臣.断续电流型开关电感Buck-Boost变换器的分岔现象［J］.哈尔滨工业大学学报，2015，47（2）：55-61.

Research on Nonlinear Behavior Control in Switched-inductor Buck-Boost Converter

WANG Lihui，TAO Caixia，TIAN Li
（School of Automation&Electrical Engineering，Lanzhou Jiaotong University，Lanzhou730070，Gansu，China）

TM46

A

10.19457/j.1001-2095.20170905

王礼辉（1988-），男，硕士研究生，Email：a124117@126.com

2016-09-06

修改稿日期：2016-11-16