基于能量机理的强迫功率振荡特性分析

李星举，王新浩

(1.国网鞍山供电公司，辽宁 鞍山 114200；2.国网承德供电公司，河北 承德 067000)

应 用 研 究

基于能量机理的强迫功率振荡特性分析

李星举1，王新浩2

(1.国网鞍山供电公司，辽宁 鞍山 114200；2.国网承德供电公司，河北 承德 067000)

使用能量函数法可以有效定位强迫功率振荡的扰动源。基于传统理论方法的能量函数，只能反映势能在电力系统中的传播和分布特性，无法说明扰动源发电机如何产生向外输出的势能。从发电机功角特性公式出发，考虑更多变量的影响，对能量函数重新进行推导，分析了扰动源发电机和非扰动源发电机相关变量的幅值相角关系，提出了一种能够解释扰动源发电机如何产生向外输出的势能及非扰动源发电机不产生向外输出势能的分析方法。在多母线双机对称系统上对提出的方法进行了仿真，分析了势能恒定分量在发电机、变压器和输电线路上的分布特性。仿真结果验证了所提分析方法的有效性。

电力系统；低频振荡；强迫功率振荡；能量函数；扰动源定位

Abstract:Energy functions could be used to locate the disturbance source of forced power oscillation effectively. Energy functions based on traditional theoretical methods can only reflect the spread and distribution characteristics of potential energy in power systems.But it can’t be used to explain how the disturbance source produce or output the potential energy. With the influence of more variables being considered, the energy functions is deduced based on the generator’s power angle formula.The relationship of the amplitudes and angels of disturbance sources related variables and non-disturbance sources are analyzed. A new analysis method is proposed which can explain how the disturbance sources be produced.It outputs the potential energy .Non-disturbance sources can’t produce or output the potential energy. A simulation is carried out on a double-generator multi-bus symmetry system.The distribution characteristic constant component of potential energy in generators, transformers and transmission lines are analyzed. The simulation results in validating the effectiveness of the proposed method.

Keywords：power system；low frequency oscillation；forced power oscillation；energy functions；disturbance source location

当电力系统发生低频振荡时，如果不及时采取有效解决措施，可能会诱发连锁反应事故，造成系统瓦解、大面积停电等灾难性后果。一般认为低频振荡的原因是负阻尼，但在实际系统中也发现一些用负阻尼机理无法解释的低频振荡现象，用强迫功率振荡机理可以有效解释这些现象。研究表明，当原动机输出的机械功率存在持续周期性小扰动时，如果扰动频率与系统的固有频率比较接近，就会导致系统中出现大幅度的功率振荡，称为强迫功率振荡[1-6]。

对于强迫功率振荡，快速定位并切除扰动源是有效的解决措施，使用能量函数法可以有效定位强迫功率振荡的扰动源。文献[7-8]从能量角度分析了强迫功率振荡时发电机内部能量的变化关系和特征；文献[9-13]在发电机能量变化的基础上提出支路势能的概念，将能量函数推广到关键支路和节点，借助网络动态信息在线识别强迫功率振荡扰动源的大致方向或位置；文献[14-15]在能量函数的基础上推导出基于参数辨识的扰动源定位方法，提出“能流方向因子”概念，用于反映势能恒定分量在电力系统中的传播和分布特性；文献[16]对能量函数法进行改进，提出利用耗散功率进行扰动源识别的方法；文献[17]构造基于联络线的能量函数，并将能量分解为振荡分量和准稳态分量；文献[18]根据振荡达到稳态时线性化系统变量关系及能量转化的特性，把强迫振荡的功率偏差和频率偏差用相量表示，将稳态的振荡过程转化为一个电路进行分析；文献[19]基于强迫功率振荡能量转换特性提出割集能量概念，根据割集能量的流向进行扰动源的识别。

文献[7-8]研究强迫功率振荡时发电机内部能量变化特性，表明扰动源发电机的势能和动能相互转换，没有向外输出的势能。

文献[9-14，19]研究使用能量函数法定位强迫功率振荡扰动源，表明扰动源发电机会向系统输出势能。

针对扰动源发电机势能如何变化这一前后矛盾的结论，本文从发电机功角特性公式出发，研究更多变量波动对发电机电磁功率波动的影响，进而对发电机势能变化特性的影响，发现了扰动源发电机向系统输出势能的电磁机理，解释了不同文献存在矛盾的原因。

在多母线双机对称系统上进行仿真验证，并分析了势能恒定分量在发电机、变压器和输电线路上的分布特性。

1 基于传统理论方法的能量函数

研究强迫功率振荡输入机械功率扰动和输出电磁功率波动量的关系，一般采用单机无穷大系统，发电机采用二阶经典模型：

(1)

式中各变量的含义见参考文献[2]，其中：

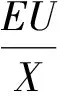
(2)

令：

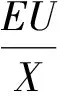
则有：

ΔPe=KΔδ

(3)

文献[7]研究强迫功率振荡时发电机内部能量变化特性，定义势能函数为

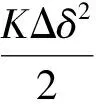
(4)

文献[9]研究使用能量函数法定位强迫功率振荡扰动源，定义势能函数为

(5)

将式(3)、式(1)代入式(5)可得：

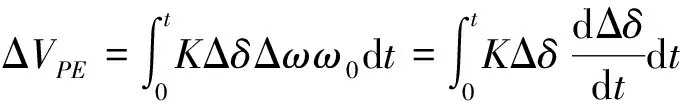
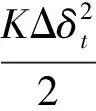
(6)

由式(6)的推导过程可知，文献[9]中定义的势能函数和文献[7]中定义的势能函数意义相同。

根据式(1)—(3)可知，在发电机内部，Δδ和Δω相角差为π/2，ΔPe和Δδ相角相同，从而ΔPeΔω是1个频率为2倍扰动频率的正弦函数；对ΔPeΔωω0进行积分，也是1个正弦函数，不存在直流分量，从而扰动源发电机只产生和动能相互转换的正弦变化的势能，不存在向外输出的势能。这个结论与文献[7-8]的研究结果相同，与文献[9-14,19]的研究结果存在矛盾。

由前述分析可知，基于传统理论方法的能量函数，在分别研究发电机内部能量变化特性和使用能量函数法定位强迫功率振荡扰动源时会得到相矛盾的结论。

产生这种矛盾的根本原因在于，建立函数时是否更加全面考虑到各种变量的影响。实际上，扰动源发电机功率波动量的表达式远非式(2)这么简单，应该考虑更多变量的影响。

2 基于发电机功角特性公式的能量函数的探索性推导

2.1电磁功率波动量推导

发电机功角特性公式[20]：

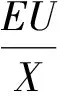
(7)

因为强迫功率振荡频率较低，所以可以忽略发电机的暂态过程。当振荡达到稳态时，在稳定输出电磁功率Pe的基础上叠加波动量ΔPe，电抗X、电势E、端电压U、功角δ均存在波动量ΔX、ΔE、ΔU、Δδ，此时有：

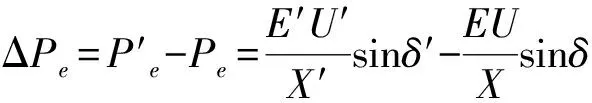
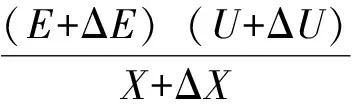
(8)

将式(8)展开可得：

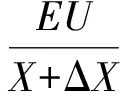
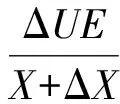
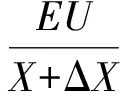
(9)

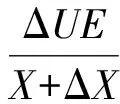
因为ΔX相比于X很小，可令X+ΔX=X；因为Δδ很小，可令cosΔδ=1，sinΔδ=Δδ，代入式(9)并化简可得：

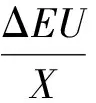
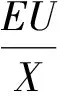
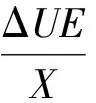
(10)

将式(10)保留一阶无穷小，忽略高阶无穷小可得：

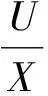
(11)

由式(11)可知，当发生强迫功率振荡时，电磁功率波动量ΔΡe不只和功角波动量Δδ有关，也和电势波动量ΔE、端电压波动量ΔU有关。

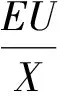
2.2电势波动量的推导

发电机电势公式[20]：

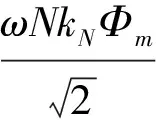
(12)

当角速度ω存在波动量Δω，磁通Φm存在波动量ΔΦm时，电势E也会存在波动量ΔE，此时有：

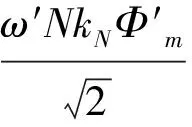
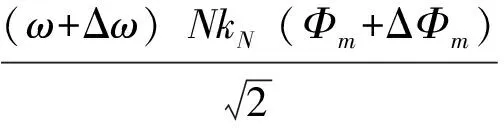
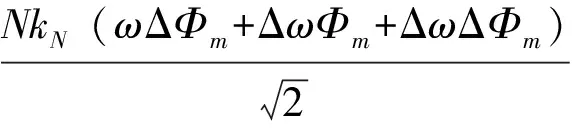
(13)

将式(13)保留一阶无穷小，忽略二阶无穷小可得：

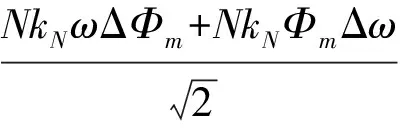
=R1ΔΦm+R2Δω

(14)

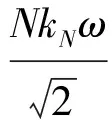
由式(14)可知，当发生强迫功率振荡时，电势受到磁通波动和角速度波动的综合影响也会发生波动，从而影响到电磁功率的波动。

2.3考虑更多变量对电磁功率波动量的影响

将式(14)代回到式(11)可得：

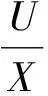
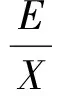
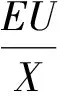
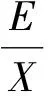
(15)

由式(15)可知，当发生强迫功率振荡时，电磁功率波动量ΔPe和功角波动量Δδ、角速度波动量Δω、磁通波动量ΔΦm、端电压波动量ΔU都有关。

对于实际的发电机，ΔU和ΔΦm的变化规律受励磁调压系统参数影响，暂时先将其忽略，只考虑式(15)的前两项则有：

ΔPe=KΔδ+rΔω

(16)

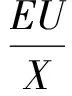
由式(16)可知，当发生强迫功率振荡时，电磁功率波动量ΔPe受到功角波动量Δδ和角速度波动量Δω的综合影响。

2.4基于发电机功角公式的能量函数推导

按照式(5)重新计算扰动源发电机内部的势能，将式(16)代回到式(5)可得：

(17)

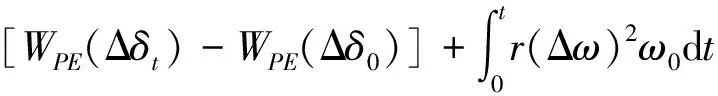
由式(17)可知，基于发电机功角特性公式推导的势能函数，其中第一项与式(6)相同，是扰动源发电机转子上产生的和动能相互转换的正弦变化的势能；第二项恒大于0，是扰动源发电机转子上产生的和向外输出的势能有关的势能直流分量。

2.5基于发电机功角公式的能量函数分析

对于扰动源发电机电磁功率波动量ΔPe，虽然KΔδ起主要作用，但由于rΔω的影响，ΔPe的相角将超前Δδ，ΔPe和Δω的相角差将小于π/2，从而ΔPeΔω除了含有1个频率为2倍扰动频率的正弦分量外，还含有1个直流分量。对ΔPeΔωω0进行积分，也存在直流分量，和扰动源发电机产生的向外输出的势能恒定分量有关。可见发生强迫功率振荡时对于扰动源发电机，Δω对ΔE的影响，进而对ΔPe的影响，是产生向外输出的势能的重要原因； Δδ对ΔPe的影响，是产生和动能相互转换的正弦变化的势能的重要原因，而对产生向外输出的势能没有直接贡献。ΔU和ΔΦm对ΔPe的影响不会使总体效果与前述分析相差太大。

对于非扰动源发电机电磁功率波动量ΔPe，KΔδ起主要作用，rΔω的影响非常小。Δω对ΔE存在同样的影响，同时由于ΔΦm的影响，会使ΔE在ΔPe上面的投影非常小，从而ΔE对ΔPe的影响非常小，即Δω对ΔPe的影响非常小。ΔPe和Δδ相角相同，ΔPe和Δω相角差为π/2，这是非扰动源发电机只产生和动能相互转换的正弦变化的势能、不产生向外输出的势能的电磁机理。ΔU对ΔPe的影响不会使总体效果与前述分析相差太大。

由前述分析可知，基于发电机功角特性公式的能量函数，和基于传统理论方法的能量函数相比，考虑了更多变量的影响，可以更合理地解释扰动源发电机和非扰动源发电机势能变化特性的异同。

此时再看式(4)和式(5)，它们的意义将不再相同。式(4)表示转子上的只与Δδ相关的部分势能；式(5)表示转子上的全部势能。当考虑更多变量影响时，文献[7-8]与文献[9-14]、文献[19]研究结果存在的矛盾即可化解。

3 仿真算例

使用BPA软件进行仿真验证，采用双机对称系统[20]，在线路上设置多个母线以便测量数据，如图1所示，发电机G1参数：转子惯性时间常数T=14 s，VN=10 kV，SN=300 MVA，Xdp=Xdq=0.31，Xd=1，Xq=0.69，Tdop=10.2，Tqop=1.5，定子漏抗为0.125。发电机G2参数：转子惯性时间常数T=27 s，其余参数同G1。发电机G1、G2励磁参数：TR=0.06 s，KA=200，TA=0.2，VRMAX=-1，KE=1，TE=1.2，SE.75MAX=0.09，SEMAX=0.368，EFDMIN=-5，EFDMAX=5，KF=0.1，TF=0.368。变压器参数，T1、T2相同：变比1∶10.5，铜损等效电阻为0.000 1，漏抗为0.006 75。母线B1到B7总共60 km，每段10 km，每段电阻为0.005，电抗为0.013。负荷P1+Q1=100+j20 MVA，负荷P2+Q2=100+j30 MVA，都是恒阻抗负荷，G1为平衡节点，出力为70.3+j28.4 MVA，G2为PV节点，出力为130+j18.9 MVA。在G1原动机轴上叠加功率幅值1 MW、角速度6.28 rad/s的正弦机械功率扰动，选取稳定振荡时的数据，进行傅里叶变换，提取相关波动量的幅值和相角。

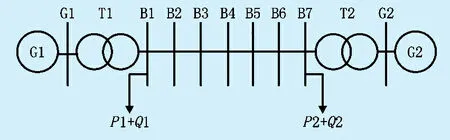
图1 多母线双机对称系统

3.1发电机G1波动量特性

表1列出了发电机G1相关波动量的幅值和相角，以功角波动量Δδ为相角基准。其中磁通波动量ΔΦm很小，可以忽略不计。

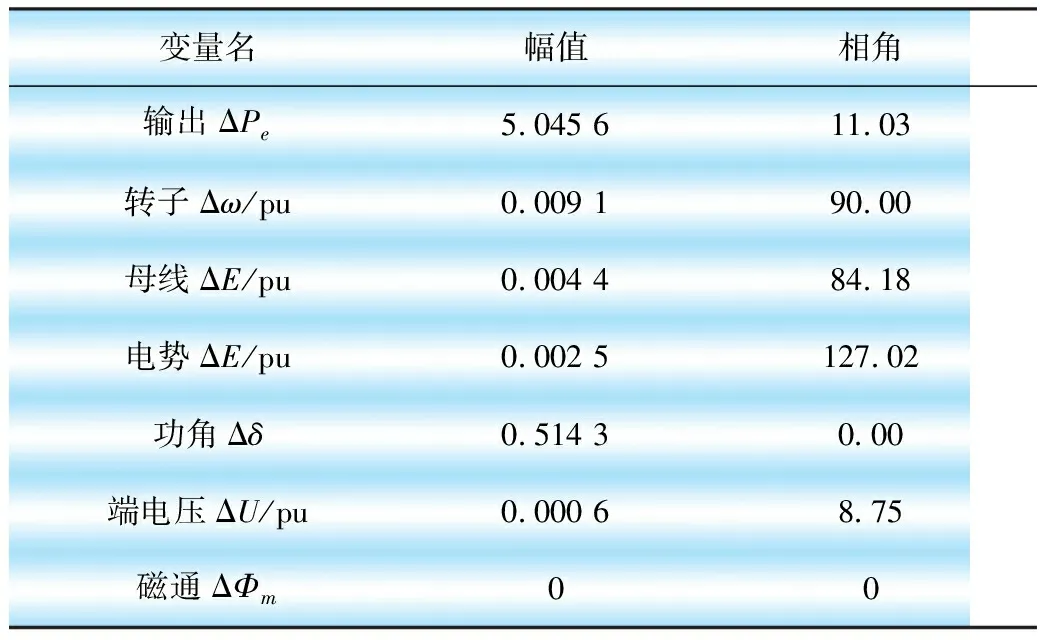
表1 发电机G1各变量的幅值和相角

将表1中各波动量的幅值进行相应缩放，以相量的形式画在同一图中，比较相角关系，如图2所示。

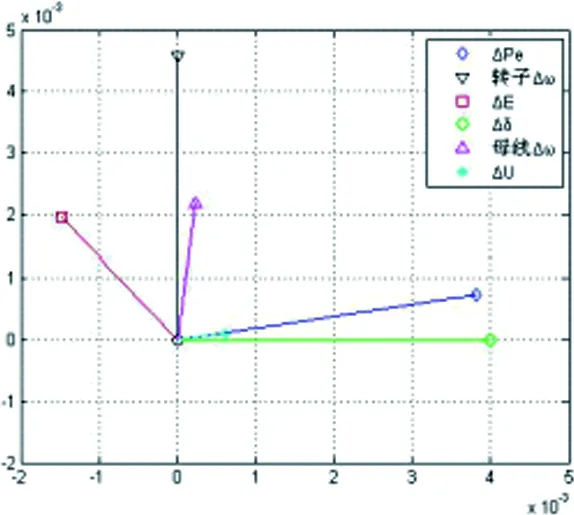
图2 发电机G1各变量的相角关系

从图2中可以看出，对于扰动源发电机，转子角速度波动量Δω相角超前功角波动量Δδ的角度为π/2，电磁功率波动量ΔPe小角度超前Δδ，和Δω的相角差小于π/2，与之前的分析一致。Δω和电势波动量ΔE的相角差小于π/2， Δω对ΔE的影响，进而对ΔPe的影响，使ΔPe相角超前Δδ，ΔPe和Δω角度差小于π/2是扰动源发电机产生势能恒定分量的重要原因。端电压波动量ΔU幅值较小，相角稍滞后于ΔPe，对ΔPe不会产生太大影响；磁通波动量ΔΦm很小，可以忽略。发电机转子角速度波动量幅值大于发电机母线频率角速度波动量，相角超前，因为扰动源发电机转子波动引领着整个系统振荡，与文献[18]的结论一致。

3.2发电机G2波动量特性

表2列出了发电机G2相关波动量的幅值和相角，以功角波动量Δδ为相角基准。其中电势波动量ΔE和端电压波动量ΔU很小，可以忽略不计。

表2 发电机G2各变量的幅值和相角

将表2中各波动量的幅值进行相应缩放，以相量的形式画在同一图中，比较相角关系，如图3所示。

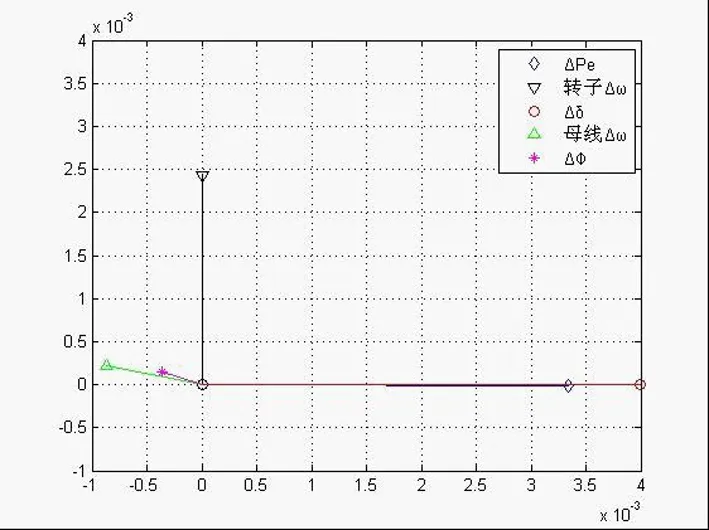
图3 发电机G2各变量的相角关系

从图3中可以看出，对于非扰动源发电机，转子角速度波动量Δω相角超前功角波动量Δδ的角度为π/2，电磁功率波动量ΔPe和Δδ的相角几乎相同，与之前的分析一致。由于ΔPe和Δω之间的角度差几乎为π/2，非扰动源发电机不产生势能恒定分量。磁通波动量ΔΦm幅值很小和ΔPe相角差接近π，对ΔPe不会产生太大影响；电势波动量ΔE和端电压波动量ΔU很小，可以忽略。发电机转子角速度波动量幅值大于发电机母线频率角速度波动量，相角滞后，因为非扰动源发电机转子波动跟随着扰动源发电机，与文献[18]的结论一致。

3.3势能恒定分量在发电机转子和母线分布特性

表3列出了发电机转子角速度波动量Δw、发电机母线和线路母线频率角速度波动量Δw、正向和反向电磁功率波动量ΔPe的幅值和相角，以发电机G1电磁功率波动量ΔPe为相角基准，正向为由G1到G2，反向为由G2到G1。

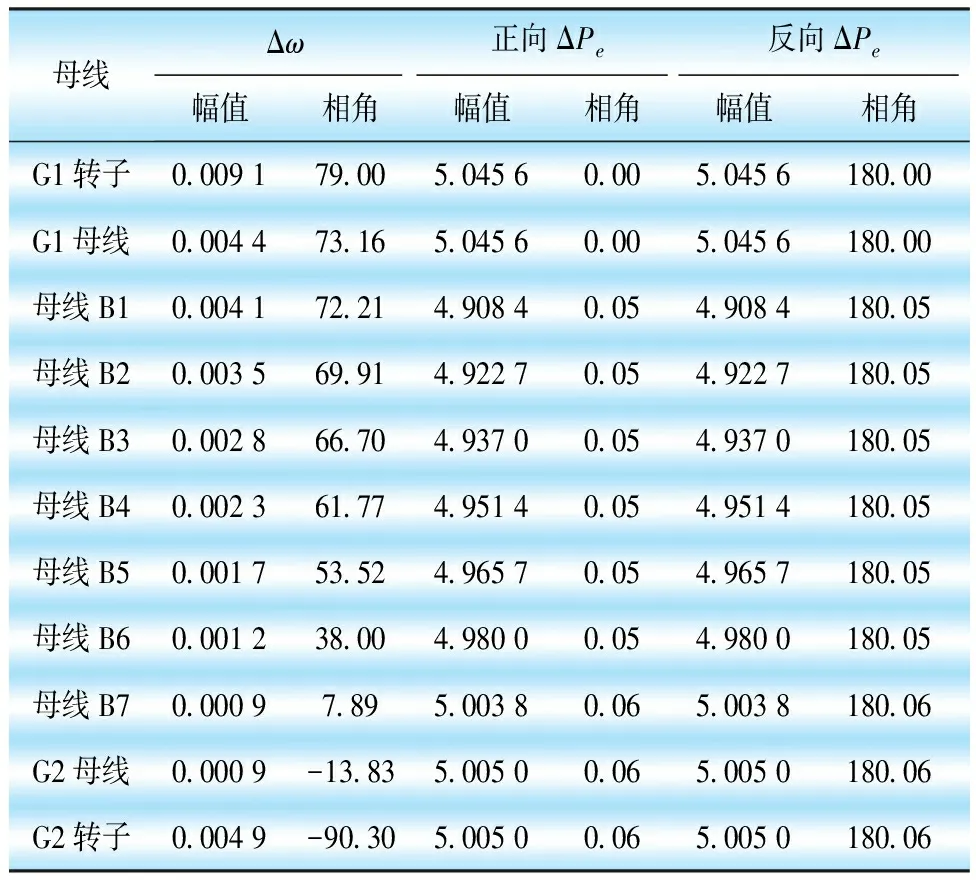
表3 角速度波动Δω和功率波动ΔPe的幅值和相角

将表3中各波动量的幅值进行相应缩放，以相量的形式画在同一图中，比较相角关系，如图4所示。

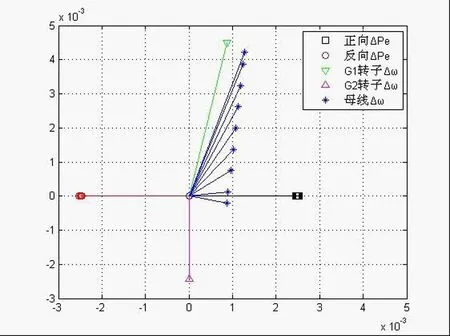
图4 角速度波动Δω和功率波动ΔPe的相角关系

由于输电线路较短，可以忽略功率波动传输的延迟时间。从图4中可以看出，正向功率波动量ΔPe在各个母线上幅值和相角相差不大，反向功率波动量ΔPe也有相同的现象。正向ΔPe和反向ΔPe相角差为π。扰动源发电机G1转子上的Δω与正向ΔPe相角差小于π/2，G1产生势能恒定分量；非扰动源发电机G2转子上的Δω与反向ΔPe相角差几乎为π/2，G2不产生势能恒定分量；母线距离扰动源越远，频率角速度波动量Δω的幅值越小，相角越滞后，在正向功率波动量ΔPe上的投影越来越小，即势能恒定分量越来越小。

可以用“能流方向因子”[14-15]反映势能恒定分量在电力系统中的传播和分布特性。表4列出了发电机转子、发电机母线和输电线路母线上正向、反向的“能流方向因子”。

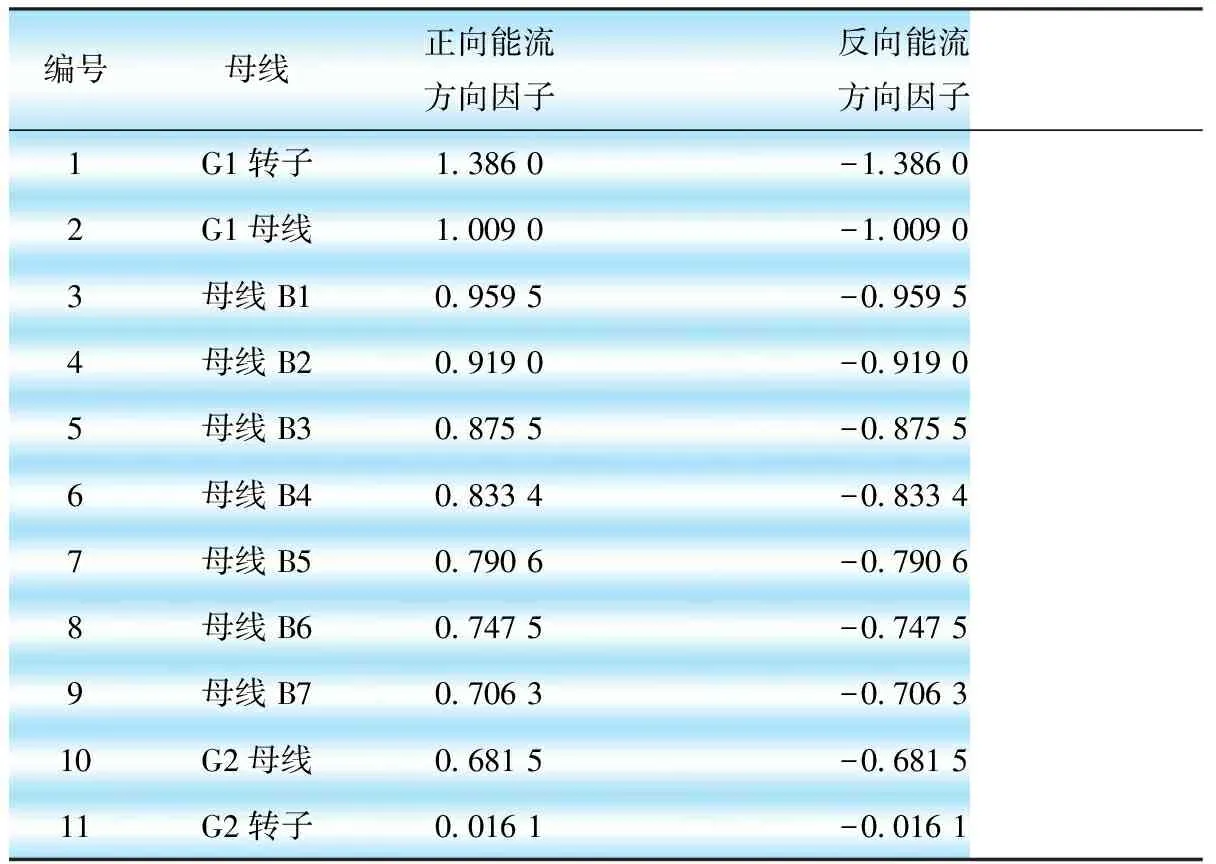
表4 能流方向因子分布

从表4中可以看出扰动源发电机转子上正向和反向能流方向因子的绝对值都是最大的，因为发生强迫功率振荡时，扰动源发电机转子是产生势能恒定分量的源头，与文献[14-15]的结论一致。还可以看出同一母线上注入和流出的势能守恒。将表4中的数据画成直线图，横坐标对应编号，如图5所示。

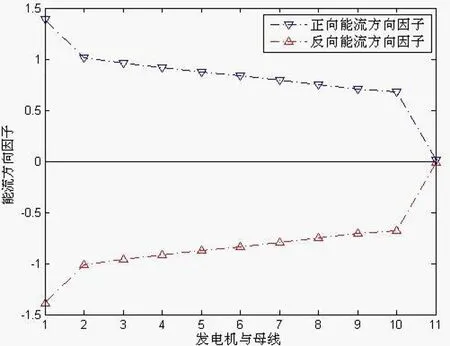
图5 能流方向因子分布

从图5中可以看出，发电机转子和发电机母线上能流方向因子的数值不同。对于扰动源发电机，转子的能流方向因子表示发电机产生的势能恒定分量，母线的能流方向因子表示发电机输出的势能恒定分量，其差值表示发电机内部阻尼消耗的能量；对于非扰动源发电机，计算过程中发现转子消耗微小的势能恒定分量，但远小于母线注入的势能恒定分量，其差值表示发电机内部阻尼消耗的能量。发生强迫功率振荡时，扰动源发电机向系统输出势能，非扰动源发电机从系统吸收势能，与文献[9，11]的结论一致。变压器上有一定的势能损耗，输电线路上也有一定的势能损耗，并且和线路长度近似呈线性关系，说明势能在传输过程中存在耗散的现象，与文献[16]的结论一致。

4 结论

本文从发电机功角特性公式出发，对强迫功率振荡能量函数进行了探索性推导，采用多母线双机对称系统进行仿真验证，得到以下结论。

a. 基于传统理论方法的能量函数，电磁功率波动量只和功角波动量有关，是无法说明扰动源发电机是如何产生向外输出的势能的。

b. 基于发电机功角特性公式，对能量函数中功率波动量重新进行推导后发现，功率波动量不只和功角波动量有关，也和电势波动量、角速度波动量、磁通波动量和端电压波动量有关。通过建立新的能量函数，可以对扰动源发电机和非扰动源发电机势能变化特性的异同给出更合理的数学解释。

c. 在多母线双机对称系统上进行仿真，通过分析扰动源发电机和非扰动源发电机相关变量的幅值相角关系，计算得出了势能恒定分量在发电机转子、发电机母线、变压器和输电线路上的分布特性，验证了所提方法的有效性。

[1] 汤 涌．电力系统强迫振荡分析[J]．电网技术，1995，19(12)：6-10．

[2] 汤 涌．电力系统强迫功率振荡的基础理论[J]．电网技术，2006，30(10)：29-33．

[3] 韩志勇，贺仁睦，徐衍会．汽轮机压力脉动引发电力系统低频振荡的共振机理分析[J]．中国电机工程学报，2008，28(1)：47-51．

[4] Vournas C D，Krassas N，Papadias B C．Analysis of forced oscillations in a multimachine power system[C]．IEE Conference Publication，British，1991

[5] 余一平，闵 勇，陈 磊，等．周期性负荷扰动引发强迫功率振荡分析[J]．电力系统自动化，2010，34(6)：7-11．

[6] 杨东俊，丁坚勇，李继升，等．同步发电机非同期并网引起强迫功率振荡分析[J]．电力系统自动化，2011，35(10)：99-103．

[7] 韩志勇，贺仁睦，徐衍会，等．基于能量角度的共振机理电力系统低频振荡分析[J]．电网技术，2007，31(8)：13-16．

[8] 黄 涌，云 雷，唐 飞，等．电力系统强迫功率振荡过程中的功能转换[J]．电力自动化设备，2013，33(8)：41-46．

[9] 余一平，闵 勇，陈 磊，等．基于能量函数的强迫功率振荡扰动源定位[J]．电力系统自动化，2010，34(5)：1-6．

[10] PAI M A．Energy function analysis for power system stability．New York，NY， USA：Kluwer Academic Publishers，1989．

[11] JING C，MCCALLEY J D，KOMMAREDDY M．An energy approach to analysis of interarea oscillations in power systems．IEEE Trans on Power Systems， 1996，11(2)：734-740．

[12] ROGERS G．Power system oscillations．New York，NY，USA：Kluwer Academic Publishers，2000．

[13] Yu Yiping，Min Yong，Chen Lei，et al．The disturbance source identification of forced power oscillation caused by continuous cyclical load[C], 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT)．Weihai，China，2011：308-313．

[14] 杨东俊，丁坚勇，李继升，等．基于参数辨识的强迫功率振荡扰动源定位方法[J]．电力系统自动化，2012，36(2)：26-30．

[15] 杨东俊，丁坚勇，邵汉桥，等．基于WAMS的负阻尼低频振荡与强迫功率振荡的特征判别[J]．电力系统自动化，2013，37(13)：57-62.

[16] 胡 伟，林 涛，高玉喜，等．基于耗散功率的区域电网强迫功率振荡扰动源定位[J]．高电压技术，2012，38(4)：1006-1011．

[17] 董 超，刘涤尘，廖清芬，等．基于能量函数的电网低频振荡及扰动源定位研究[J]．电网技术，2012，36(8)：175-181．

[18] 杨毅强，刘天琪，李兴源，等．电力系统强迫功率振荡的等效电路定位分析法[J]．电网技术，2012，36(11)：101-108．

[19] 王娜娜，廖清芬，唐 飞，等．基于割集能量及灵敏度的强迫功率振荡扰动源识别[J]．电力自动化设备，2013，33(1)：75-80．

[20] 戴文进，徐龙权．电机学[M]．北京：清华大学出版社，2009，67-72.

Analysis of Forced Power Oscillation Based on Energy Mechanism

LI Xingju1,WANG Xinhao2

(1.State Grid Anshan Power Supply Company，Anshan，Liaoning 114200,China; 2. State Grid Chengde Power Supply Company,Chengde,Hebei 067000,China)

TM712

A

1004-7913(2017)07-0025-07

2017-04-28)

李星举(1989)，男，硕士，助理工程师，从事变电检修相关工作。