曲线顶管施工引起的地表变形预测研究

张 鹏， 李志宏， 曾 聪， 马保松

(1. 中国地质大学(武汉)工程学院， 湖北 武汉 430074；2. 广东省南粤交通投资建设有限公司， 广东 广州 510101)

曲线顶管施工引起的地表变形预测研究

张 鹏1， 李志宏2， 曾 聪1， 马保松1

(1. 中国地质大学(武汉)工程学院， 湖北 武汉 430074；2. 广东省南粤交通投资建设有限公司， 广东 广州 510101)

为了研究曲线顶管施工引起的地表变形，通过分析拱北隧道管幕工程曲线顶管现场实测数据，得出曲线顶管地表沉降槽的偏移曲线； 在现有Peck和Loganathan地表变形计算公式的基础上，考虑曲线顶管与隧洞的相对位置对沉降槽偏移量的影响，得出经过沉降槽偏移修正的Peck和Loganathan地表变形预测公式。结果表明： 1)曲线顶管施工引起的地表沉降槽曲线表现为非对称，最大沉降点可能出现在轨迹弯曲内侧，也可能偏向外侧； 2)曲线顶管与隧洞相对位置引起的土体损失变化是造成沉降槽偏移的主要原因，相对位置与顶管穿越地层性质、顶进力、注浆压力和轨迹曲率半径等因素有关； 3)修正的Peck公式可以较好地反映砂层和淤泥质土层中曲线顶管施工地面沉降槽偏移效应和最大沉降量。

曲线顶管； 地表变形； 变形预测； 土体损失； 沉降槽偏移

Abstract: The field deformation data monitored in curved pipe jacking of Gongbei Tunnel are analyzed; and the deviation curve of the ground settlement groove is obtained. And then ground settlement prediction formulas of Peck and Loganathan modified by deviation of ground settlement groove are obtained based on existing Peck and Loganathant formulas considering influence of relative position of curved pipe jacking and tunnel on deviation of ground settlement groove. The results show that: 1)The pipe jacking induced ground settlement groove curve shows asymmetry; and the maximum settlement point would occur to inside/outside of the curve. 2)The deviation of ground settlement groove mainly lies on soil loss induced by relative position of curved pipe jacking and tunnel; and the relative position of curved pipe jacking and tunnel can be affected by ground properties, jacking force, grouting pressure and curvature radius. 3) The modified Peck formula can well reflect the deviation of ground settlement groove and maximum settlement during pipe jacking in sandy stratum and silt soil stratum.

Keywords: curved pipe jacking; ground deformation; deformation prediction; soil loss; deviation of ground settlement groove

0 引言

随着我国地下设施不断增多，新建地下工程施工(如地铁隧道、地下管网等)必然面临拥挤的地下空间限制的问题，并可能会对已有地下结构产生影响。曲线顶管作为一种非开挖地下工程施工技术，由于可以使管道沿设计曲线轨迹顶进，被广泛应用于城市供排水、油气、通信电力以及地铁等管道和隧道工程中。

然而，在曲线顶管施工过程中，会不可避免地引起周边地层变形。目前，国内外学者对于直线顶管引起的土体变形进行了深入研究，主要考虑土体损失、正面附加推力、管道与岩土体侧摩阻力以及注浆压力等因素的影响，采用经验公式法、随机介质理论、弹性力学解析法和数值模拟等方法对土体变形进行了详细研究，其结果均表明直线顶管施工引起的地表变形曲线关于隧洞轴线对称。

然而，目前对曲线顶管引起土体变形方面的研究较少，并且不同学者得出的结论存在明显差异。由广明等[1]通过建立三维曲线顶管有限元模型和现场监测研究曲线顶管土体变形规律，得出了由于管道外侧存在土体抗力，地面沉降槽并不关于隧洞轴线对称，最大值偏向曲线圆心一侧。潘同燕[2]对现场曲线顶管管土接触压力监测研究也表明管道弯曲内侧润滑泥浆压力大于外侧，可见管道弯曲内侧间隙大于外侧，也证明了管道向轨迹曲线外侧偏移。然而，同样对于曲线顶管引起的地表变形问题，陈思甜等[3]采用数值模拟和现场监测的研究结果表明，地表沉降槽不关于隧洞轴线对称，但是最大沉降点却偏向顶管轨迹弯曲外侧，与由广明等[1]的研究结果恰好相反。综上所述，可以确定的是曲线顶管引起的地表沉降槽具有不对称的特点，但是沉降槽具体偏移方向研究结论尚不明确，说明引起偏移的本质因素还有待进一步研究。

本文在现场曲线顶管施工地表变形监测的基础上，提出顶管与隧洞相对位置引起的土体损失变化是造成沉降槽偏移的原因，上述2种偏移方向都可能出现，其偏移方向受地层性质、顶进力、润滑注浆压力和曲率半径等参数影响；在考虑土体损失造成的沉降槽偏移基础上，对直线顶管地表变形公式进行修正，得出曲线顶管土体变形预测公式。

1 现场监测研究

1.1工程概况与测点布置

1.1.1 工程概况

港珠澳大桥珠海连接线拱北隧道暗挖段采用曲线管幕支护与冻结止水相结合的创新技术下穿拱北口岸。管幕断面如图1所示，暗挖段长度为255 m，平面线形由88 m缓和曲线与167 m圆曲线组成；管幕上部平均埋深为4～5 m，总体高度约为23.8 m，宽度约为22.2 m，开挖面积达到336.8 m2。整个管幕由36根直径1 620 mm的钢管组成，其中上层17根钢管壁厚20 mm，下层19根钢管壁厚24 mm，管间距355～358 mm，采用F型接头连接。所有钢管通过东、西2个工作井实现双向顶进[4-7]。

为了对整个管幕顶管关键技术进行前期验证，在全面顶进施工前，现场顶进2根试验管(0#和5#管)。其中0#试验管为附加顶管，平面布置如图2所示，其顶部覆土厚度为5.5～6.5 m，由东工作井始发，西工作井接收； 5#试验管为管幕原位顶管，顶进方向与0#试验管相反。

图1 拱北隧道曲线顶管管幕剖面图(单位： m)

Fig. 1 Cross-section of curved jacking pipe roofing of Gongbei Tunnel (unit: m)

图2 0#试验管平面图

1.1.2 测点布置

为监测整个管幕施工过程中的地面变形，现场沿管幕轴线方向共布置24个监测断面，相邻2个监测断面之间的距离为10 m，每个监测断面上共设置16个监测点，相邻2个监测点距离2 m，如图3所示，采用水准仪监测各点沉降值。由于受口岸中车辆和人流影响，只对部分断面进行了完整监测，同时考虑0#试验管主要穿越砂层和淤泥质土，因而选取代表性监测断面CJ4和CJ20进行研究。2个监测断面地层情况如表1所示，顶管在CJ4断面主要穿越砂层，而CJ20位于淤泥质土层。CJ4-6测点距离0#管中心距离t为0.12 m，CJ20-6测点与0#管中心距离t为-0.41 m(t正值为轨迹外侧，负值轨迹内侧)。

图3 某监测断面地表变形部分测点布置图

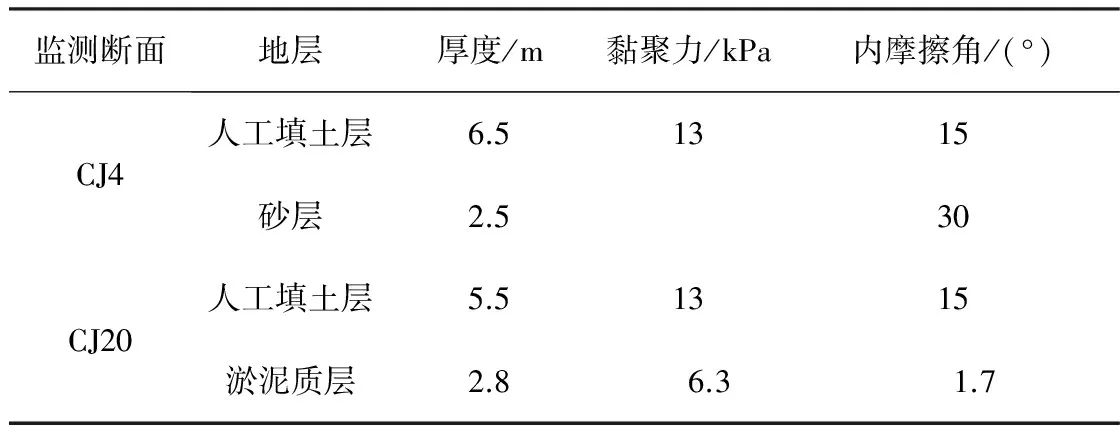
表1 监测断面地层参数

1.2变形监测结果

顶管穿越砂层和淤泥质层引起的地表变形如图4所示(正值表示沉降变形，负值表示隆起变形)。由图4可知： 曲线顶管施工引起的地面沉降槽曲线并不关于隧洞轴线对称，最大沉降点存在一定的水平偏移，沉降值随着两侧水平距离的增大而减小。砂层中最大沉降为4.1 mm，偏向顶管轨迹曲线外侧，沉降槽曲线具有一定对称性。随着水平距离增大，曲线两侧对称性不明显，顶管轨迹曲线内侧沉降槽相对外侧更宽缓，沉降值也相对较小，说明外侧受顶管扰动更显著； 淤泥质层中最大沉降为1.8 mm，偏向顶管轨迹曲线内侧，整个沉降槽曲线没有明显对称性，顶管轨迹曲线内侧沉降槽相对外侧更窄，沉降值相对外侧也较小，表现为轻微隆起，说明外侧受顶管扰动更显著。

图4 不同地层地面沉降槽实测曲线

Fig. 4 Measured ground settlement curves in different formations

以上监测结果表明，对于曲线顶管地表沉降槽偏转方向并不是固定不变的。即使对于同一根顶管管道，随着顶进距离和穿越地层的不同，其沉降槽偏移方向也可能不同。而文献[1，3]中都认为其存在单一方向的偏移模式，显然是不全面的，其偏移方向与施工参数和地层等因素相关。

2 变形公式推导

2.1现有公式

目前，常用于直线顶管地表变形预测的公式主要为Peck经验公式和镜像法解析公式，二者都将土体损失作为顶管施工导致土体变形的主要因素，以下对2种公式做简要说明。

2.1.1 经验公式

Peck[8]在大量统计隧道施工地表变形的基础上，采用正态分布曲线来拟合地面沉降槽，认为土体变形仅由土体损失造成。假定土体不排水、体积不可压缩(泊松比μ=0.5)，则沉降槽体积等于土体损失体积，得出隧道施工引起的横向地面沉降经验公式，并被扩展到顶管和盾构领域。

(1)

(2)

式(1)—(2)中：x为距隧洞轴线的水平距离；S(x)为x处地面沉降量；Smax为隧洞轴线上方最大地面沉降量；Vloss为顶管单位长度的土体损失量；i为地面沉降槽宽度系数，即沉降槽曲线拐点离隧洞轴线的水平距离。

O′Reilly等[9]通过统计各种地质条件下开挖隧道引起地面沉降实测值，得到3 m

黏土：i=0.43h+1.1；

(3)

粒状土：i=0.28h-0.1。

(4)

式(3)—(4)中h为隧道中心埋深，m。

2.1.2 解析公式

Sagaseta[10]假定土体损失为沿隧道轴向均匀分布的圆柱体，同样在土体不排水、体积不可压缩的条件下，采用等量径向移动模式，利用镜像法得到地面沉降计算公式。Verruijt等[11]利用Sagaseta的方法，考虑隧道表面的均匀径向位移和隧道长期椭圆变形影响，得到任意泊松土体半平面条件下竖向和水平位移解析解。Loganathan等[12]在结合Verruijt等解析解的基础上，采用椭圆形非等量径向土体移动模式提出改进的地面沉降计算公式

(5)

式中Rt为隧洞半径。

上述2种土体变形预测公式均以土体损失为影响因素，因此隧道单位长度内土体损失体积Vloss是关键计算参数。目前其计算方法主要有2种： 1)经验方法。根据施工经验和参数反演得到合适的土体损失百分率η来估算土体损失的大小，因此，土体损失体积可表示为式(6)。 2)根据Lee等[13]提出的等效土体损失参数g按照式(7)进行计算。

(6)

(7)

2.2沉降槽偏移计算

曲线顶管过程中，管节受力及其与隧洞孔壁的相互作用如图5所示，相邻管节偏角为β。对于第n根管节，其受到后续管节的顶力Fjn，前方第n-1管节的顶力反作用Fj(n-1)，内侧压力Fin，外侧压力FOn以及摩阻力f。现场管土压力实测表明其内外侧压力并不相等，因此，当外侧压力、顶进力和管节偏角较小时，且FOn>Fin+Fj(n-1)sinβ，则管节向轨迹曲线内侧偏移，管节与隧洞孔壁内侧接触。此时，在孔壁稳定的条件下，其管节外侧压力仅为润滑泥浆压力，而管节与孔壁接触一侧接触压力为土压力和润滑泥浆压力的总和。反之，当管节外侧压力较小，顶进力和管节偏角较大时，其偏转方向相反。因此，曲线顶管与隧洞的相对位置及偏移方向取决于润滑泥浆压力、顶进力及轨迹曲率的大小，在这三者影响下，管节既可能发生外偏也可能发生内偏，而之前的研究往往仅基于管节外偏的假设，认为管节与隧洞孔壁外侧接触，土体抗力仅存在于管节外侧，引起的地面沉降槽向内侧偏移，显然并不全面。

图5 曲线顶管管节受力示意图

图6 沉降槽偏移计算示意图

(8)

(9)

(10)

式(8)—(10)中： ΔR为管道轴向偏移距离；Rp为顶管管道半径；L为沉降槽偏移隧洞中心距离。

将Rt=0.838 m、Rp=0.81 m带入非线性方程式(10)中，可得管道偏移量与沉降槽偏移量的关系曲线，如图7所示。由图7可知： 沉降槽偏移距离随着管道轴向偏移增大而增大，当ΔR=Rt-Rp时，沉降槽偏移距离为0.52 m。

图7 沉降槽偏移与管道轴线偏移关系曲线

Fig. 7 Curve of relationship between deviation of ground settlement groove and that of pipe axis

2.3曲线顶管地表变形预测公式

虽然在顶管施工中影响土体变形的因素很多，但大部分施工参数在施工过程中波动比较剧烈，并且现场缺乏有效的记录，考虑到土体损失为引起土体变形的主要因素，因此本文仅考虑土体损失对顶管施工地表变形的影响。

2.3.1 土体损失体积计算

关于土体损失的计算，本文采用式(6)，通过前人总结的不同地层土体损失百分率η，对现场变形实测数据进行反算，选取一个合理的η值。魏纲[14]对土体损失率的统计分析表明，主要集中在0.20%～2.0%，对于黏土η通常为0.5%～2.5%，对于砂层η为0.97%～3.01%；而文献[15]结果表明淤泥质层实测反算值η为0.22%～1.22%。因此，后续计算中土体损失率取平均值，其中砂层η=1.67%，淤泥质层η=0.72%。

2.3.2 考虑偏移的地表变形公式

考虑上述分析中曲线顶管与孔壁的相对位置引起的沉降槽偏移规律，在采用Peck公式预测曲线顶管土体变形计算时，可引入偏移量L对式(1)进行修正，可得：

(11)

式(11)中除L以外的其他参数计算与直线顶管情况下相同； 坐标系原点为隧道中心，x轴正方向为顶管轨迹弯曲外侧，负方向为弯曲内侧；L根据式(10)计算，取值规定为管节偏向顶管轨迹内侧时，L取正值，反之取负值。

同样，对于Loganathan和Poulos提出的椭圆形非等量径向土体移动下的地面沉降按式(5)进行偏移量修正：

(12)

2.4工程实例对比分析

为验证本文修正公式的可靠性，将修正的Peck公式(11)和修正的Loganathan公式(12)与实测数据进行比较，由于顶管上覆主要为人工填土，地表沉降槽宽度系数i采用式(3)计算。具体计算参数取值：Rt=0.838 m，Rp=0.81 m，ΔR=Rt-Rp=0.028 m，h=6 m，i=3.68 m；砂土层η=1.67%，μ=0.3，L=-0.52 m； 淤泥质土层η=0.72%，μ=0.42，L=0.52 m。地面沉降计算与实测结果的对比如图8所示。

(a) 砂层 (b) 淤泥质土层

图8地面沉降计算与实测对比图

Fig. 8 Comparison between calculated ground settlement and monitored results in stratum

由图8(a)可得，通过偏移修正的Peck公式和Loganathan公式沉降槽偏移规律与实测值基本一致，2个公式在距离轴线较远处沉降值相差不大，但在轴线附近相差较大，修正的Loganathan公式计算值明显大于修正的Peck公式计算值。与实测值相比，修正的Peck公式计算值在最大沉降计算值附近十分吻合，但在两侧较远处，计算值略小于实测沉降值，说明对于砂土层，修正的Peck公式可以描述曲线顶管地表沉降槽偏移效应，并可预测最大沉降点附近的地表变形。

由图8(b)可得，经过偏移修正的Peck公式和Loganathan公式计算的沉降槽曲线数值上相差不大，但修正的Peck公式最大沉降计算值与实测值更接近。二者计算值右侧曲线与实测值比较吻合，但左侧相差较大，实测值表现为轻微隆起，说明对于淤泥质土层，采用修正的Peck公式同样可以描述曲线顶管地表沉降槽偏移效应，并预测最大沉降值。

3 结论与讨论

通过对曲线顶管施工引起的地表变形进行现场监测和分析，得到以下结论：

1)现场地表变形监测结果表明，曲线顶管施工引起的地表沉降槽曲线表现为非对称，最大沉降点既可能出现在轨迹弯曲内侧，也可能出现在外侧。砂层中沉降槽偏向顶管轨迹曲线外侧，而在淤泥质土层中沉降槽却偏向内侧，其偏移方向并不是固定的。

2)曲线顶管管节和隧洞的相对位置与顶管穿越地层性质、顶进力、注浆压力和轨迹曲率半径等因素相关，且曲线顶管管节与隧洞的相对位置引起土体损失重新分布是导致最大沉降点偏移的主要原因。

3)基于沉降槽偏移修正的Peck公式可以较好地反映砂层和淤泥质层中沉降槽的偏移效应和最大沉降量，可以作为预测相应地层曲线顶管地表变形的依据。

4)由于本文主要考虑顶管施工土体损失引起的地层变形，后续有待进一步开展曲线顶管由于管周非均匀的注浆压力及土压力引起的地层变形。

[1] 由广明,朱合华,刘学增,等. 曲线顶管施工环境影响的三维有限元分析[J]. 地下空间与工程学报, 2007(2): 218. YOU Guangming, ZHU Hehua, LIU Xuezeng, et al. 3D finite element analysis of influence of curved pipe-jacking construction on environments[J]. Chinese Journal of Underground Space and Engineering, 2007(2): 218.

[2] 潘同燕. 大口径急曲线顶管施工力学分析与监测技术研究[D]. 上海: 同济大学, 2000. PAN Tongyan. Research of mechanics analysis and monitoring technology during large diameter sharp curved pipe jacking construction[D]. Shanghai: Tongji University, 2000.

[3] 陈思甜, 何剑星, 张永兴, 等. 超浅层小半径曲线顶管地面扰动数值模拟分析[J]. 重庆交通大学学报(自然科学版), 2009, 28(5): 861. CHEN Sitian, HE Jianxing, ZHANG Yongxing, et al. Numerical simulation of ground disturbance of extra-shallow-underground-pipe jacking with short-radius curve[J]. Journal of Chongqing Jiaotong University(Natural Science), 2009, 28(5): 861.

[4] 潘建立, 高海东, 史培新. 拱北隧道暗挖段管幕组合方案优化研究[J]. 现代隧道技术, 2015, 52(3): 55. PAN Jianli, GAO Haidong, SHI Peixin. A study of combined pipe-roof scheme optimization for the bored section of the Gongbei Tunnel[J]. Modern Tunnelling Technology, 2015, 52(3): 55.

[5] 李志宏, 李剑. 曲线顶管管幕间相互影响研究[J]. 现代隧道技术, 2015, 52(3): 63. LI Zhihong， LI Jian. A study of the interaction between the pipes of a curved pipe-roof[J]. Modern Tunnelling Technology, 2015, 52(3): 63.

[6] 程占, 程勇, 刘志刚. 拱北隧道管幕-暗挖法工作井设计关键技术[J]. 隧道建设, 2015, 35(11): 1214. CHENG Zhan, CHENG Yong, LIU Zhigang. Key technologies for design of working shaft of Gongbei Tunnel: Considering tunneling and pipe jacking conditions [J]. Tunnel Construction, 2015, 35(11): 1214.

[7] 张鹏, 潘建立, 刘应亮, 等. 拱北隧道曲线顶管管幕施工关键技术[J]. 隧道建设, 2016, 36(8): 968. ZHANG Peng, PAN Jianli, LIU Yingliang, et al. Key construction technologies for curved jacking pipe roofing of Gongbei Tunnel[J]. Tunnel Construction, 2016, 36(8): 968.

[8] PECK R B. Deep excavations and tunneling in soft ground[C]//Proceeding of 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: State of the Art Report, 1969: 225.

[9] O′REILLY M P, NEW B M. Settlements above tunnels in the united kingdom-their magnitude and prediction[C]//Proceedings of Tunneling 82. London: Institution of Mining and Metallurgy, 1982: 173.

[10] SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301.

[11] VERRUIJT A, BOOKER J R. Surface settlements due to deformation of a tunnel in an elastic half plane[J]. Géotechnique, 1996, 46(4): 753.

[12] LOGANATHAN N, POULOS H G. Analytical prediction for tunneling-induced ground movement in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846.

[13] LEE K M, ROWE R K, LO K Y. Subsidence owing to tunneling I: Estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929.

[14] 魏纲. 盾构隧道施工引起的土体损失率取值及分布研究[J]. 岩土工程学报, 2010, 32(9): 1354. WEI Gang. Selection and distribution of ground loss ratio induced by shield tunnel construction[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1354.

[15] 李忠超,陈仁朋,孟凡衍,等. 软黏土中盾构掘进地层变形与掘进参数关系[J]. 浙江大学学报(工学版), 2015, 49(7): 1268. LI Zhongchao, CHEN Renpeng, MENG Fanyan, et al. Tunnel boring machine tunneling-induced ground settlements in soft clay and influence of excavation parameters[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(7): 1268.

PredictionofGroundDeformationInducedbyCurvedPipeJacking

ZHANG Peng1, LI Zhihong2, ZENG Cong1, MA Baosong1

(1.FacultyofEngineering,ChinaUniversityofGeosciences(Wuhan),Wuhan430074,Hubei,China; 2.GuangdongNanyueTransportationInvestment&ConstructionCo.,Ltd.,Guangzhou510101,Guangdong,China)

U 455.4

A

1672-741X(2017)09-1120-06

2017-01-17;

2017-04-26

交通运输部项目(201331J11300)

张鹏(1988—)，男，山西大同人，中国地质大学(武汉)地质工程专业在读博士，研究方向为顶管等非开挖技术和理论。E-mail： cugpengzhang@163.com。 *通信作者： 马保松， E-mail： mabaosong@163.com。

10.3973/j.issn.1672-741X.2017.09.009