基于蒙特卡洛方法的支撑剂导流能力不确定度评价

陶祖文

（中国石化西南石油工程有限公司井下作业分公司，四川德阳 618000）

基于蒙特卡洛方法的支撑剂导流能力不确定度评价

陶祖文

（中国石化西南石油工程有限公司井下作业分公司，四川德阳 618000）

为解决压裂支撑剂充填层导流能力测量不确定度评定时数学模型过于复杂以及部分偏导数难以求解的问题，本论文采用蒙特卡洛方法对支撑剂充填层导流能力不确定度进行评价，推导了概率密度函数对应的随机变量的获取公式，研究表明试验次数在10万～100万次之间，采用蒙特卡洛方法计算出的估计值和标准不确定度结果稳定，并且试验次数越大，精确度越高。

蒙特卡洛法；压裂；支撑剂；导流能力；测量不确定度

测量不确定度是指由于测量误差的存在，对被测量值不能肯定的程度，是表征测量质量的重要指标[1，2]。根据CNAS-CL07关于测量不确定度的要求[3]，在客户有要求或不确定度影响到对结果符合性的判定时，校准实验室必须对校准数据给出不确定度及评定程序。目前，测量不确定度已在油气计量领域得到广泛的应用[4]，但是受到各不确定度分量大小不相近、测量模型的偏导数难以求得、输入量的概率密度函数不对称等方面的限制。

但是，蒙特卡洛法为测量不确定度评定提供了一个通用的数值方法，适用于任意多个由概率密度函数表征的输入量和单一输出量的模型[5]。蒙特卡洛方法又称随机模拟方法，它以概率理论为基础理论，以随机抽样为主要手段[6]。国外学者Willink R[7]、Esward T J等[8]研究了蒙特卡洛方法在不确定度评定中的应用，Crowder S V等[9]、Hall B D[10]研究了二阶蒙特卡洛方法在非线性方程和小样本量测试中的不确定度评定中的应用，Fernández M S等[11]研究了自适应蒙特卡洛方法的不确定度评定方法。国内该领域研究方面，祖先锋等[12]、王珊等[13]、高玉英[14]以蒙特卡洛方法为基础，在现代测试及仪器精度领域进行了不确定度评定。本文详细阐述了蒙特卡洛方法评定步骤及随机数的获取方法，并以油气计量领域实例进行说明。

1 蒙特卡洛方法及不确定度评定步骤

蒙特卡洛方法的基本思想是针对所要求解的问题，对各个输入量的概率密度函数进行依次输入，抽样时调用相关函数产生服从相应概率分布的随机数，结合建立的数学模型及最大信息熵原理进行数值仿真，从而获得数学模型的方差、期望值、包含区间等参数。蒙特卡洛方法不确定度评定流程图（见图1）。

图1 蒙特卡洛方法不确定度评定步骤

1.1 建立数学模型

当输出量 Y 是由相应的输入量 X=（X1，X2，…，XN）确定时，建立的数学模型即为：

式中：X=（X1，X2，…，XN）。

1.2 输入量的确定

输入量的确定主要是基于贝叶斯定理及最大熵原理，根据已有的实验数据、计量理论及经验，为每个独立的输入量确定概率密度函数，常见的统计分布（见表1）。

表1 常见的输入量信息及其对应的概率密度函数

1.3 试验次数M的确定

蒙特卡洛方法产生的误差ε[15]：

式中：ε-误差；λa-置信度a对应的值；σ-均方差；M-数值计算次数。

由公式（2）可知，试验次数M对于蒙特卡洛方法测量不确定度具有重要作用，M值越大，通过仿真模拟产生的误差越小，M值越小，产生的误差就会增大，输出值就会失真。

当测量结果的不确定度取小数点后两位有效数字时：

其中，自由度的公式为：

式中：v-自由度；μ（y）-标准不确定度。

可知M≥2×104，所以M取值105～106即可满足要求。

1.4 输入量随机数的获取方法

考虑到统计分布函数与获取的真实值之间的一致性，实验测量数据预测宜采用矩形分布、正态分布及三角分布等。这里以三角分布为例，分析如何产生服从三角分布的随机数。通过计算机产生均匀分布的伪随机数ur～[0，1]，三角分布的概率密度函数为：

其中：a'-三角形分布的底限，c'-众数（最可能值），b'-上限，其分布函数为：

反函数变换为：

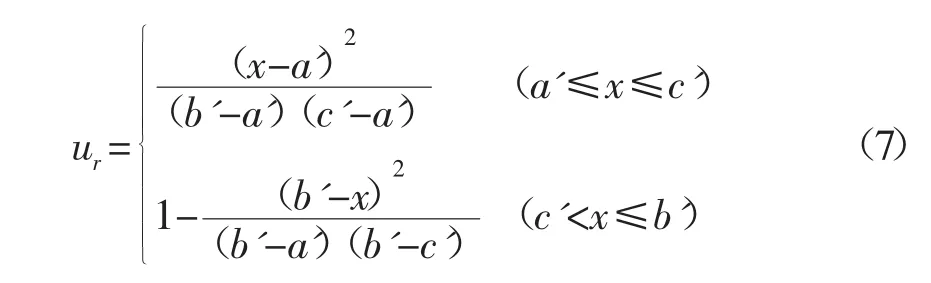
从而得到需要的随机数：

其他分布形式的概率密度函数以及随机变量产生方法（见表 2）。

表2 概率密度函数对应的随机变量

2 支撑剂充填层短期导流能力不确定度评定实例

2.1 测量流程及测量模型

图2 测量流程图

表3支撑剂充填层导流能力数据表

压裂支撑剂充填层短期导流能力的测量以支撑裂缝导流仪为基础，通过程序采集得到岩心夹持器两端的压差以及液体流量，即可通过公式求得支撑剂充填层导流能力，测量流程图（见图2）。

具体的测量模型为：

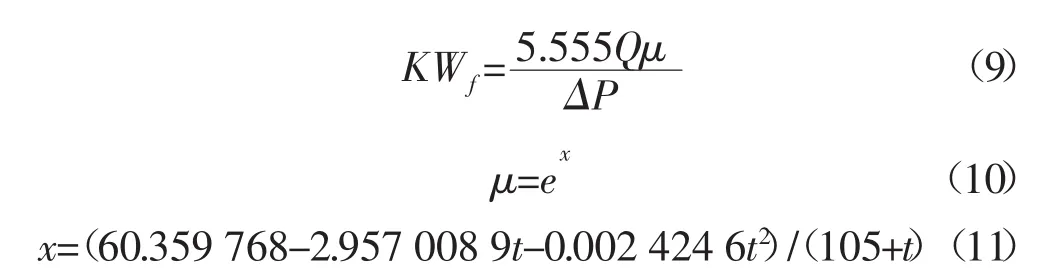
式中：KWf-支撑剂充填层的导流能力，μm2·cm；Q-流量，cm3/min；μ-黏度，mPa·s；ΔP-压差，kPa；t-温度，°C。

2.2 测量数据

根据SY/T 6302-2009《压裂支撑剂充填层短期导流能力评价推荐方法》，环境温度为24℃，在蒸馏水或去离子水温度为24℃时，其黏度为0.911MPa·s。在闭合压力为6.89MPa的条件下进行8次独立测量，观察记录岩心夹持器两端的压差及液体流量，具体实验数据（见表 3）。

2.3 采用蒙特卡洛方法进行不确定度评定

2.3.1 建立数学模型 支撑剂充填层导流能力测量的数学模型为式（9）～式（11）。

2.3.2 输入量的确定

（1）压差的确定：压力变送器的最大允许误差为±0.5%，在闭合压力6.89MPa时，压差的平均值为0.667 kPa，下限 a为 0.664 kPa，上限 b 为 0.670 kPa。根据最大熵原理，压差设定为矩形分布R（0.664，0.670）。

（2）流量的确定：查阅计量泵的校准证书可知，流量为10 mL/min时的扩展不确定度为1.2%，包含因子k=2，则标准不确定度为0.6%。因此，流量的最佳估计值为10 mL/min，根据最大熵原理，流量设定为正态分布 N（10，0.0062）。

（3）黏度的确定：由公式（10）可知，黏度的确定与温度直接相关。查阅温度传感器的校准证书可知，温度为24℃时的扩展不确定度为0.13℃，包含因子k=2，则标准不确定度为0.065℃。因此，温度的最佳估计值为24℃，根据最大熵原理，温度设定为正态分布N（24，0.0652），黏度由温度随机数获得。

2.3.3 MATLAB编程及总结报告 以蒙特卡洛方法为基础，利用MATLAB软件进行计算（代码见附件1），试验次数分别取10万、50万、100万次，输出量的估计值及标准不确定度分别按公式（12）、公式（13）求取：

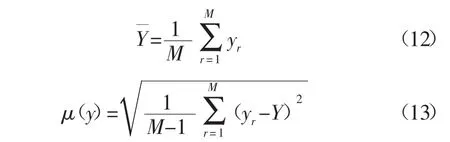
式中：yr-不同输入量对应的支撑剂充填层导流能力，μm·2cm；不同支撑剂充填层导流能力的平均值，μm2·cm；μ（y）-支撑剂充填层导流能力的标准不确定度，μm2·cm。

计算结果（见表4、图3～图5）。可以看出，试验次数在10～100万次时，估计值及不确定度保留小数点后两位小数时，导流能力估计值均为75.88 μm2·cm，标准不确定度均为0.23 μm2·cm，蒙特卡洛方法计算结果稳定。同时，试验次数越大，概率对称的95%的包含区间越小，概率密度曲线越集中，精确度越高。

3 结论

（1）用蒙特卡洛方法进行不确定度评定适用于具有单一输出量、输入量能够近似为概率密度函数的任意模型，特别是测量公式过于复杂或偏导数难以确定的数学模型。

表4 支撑剂充填层导流能力数值计算结果

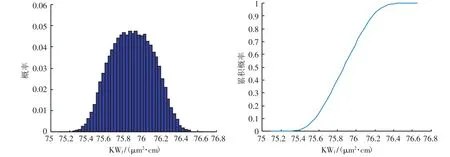
图3 试验次数为10万次的导流能力计算结果

图4 试验次数为50万次的导流能力计算结果

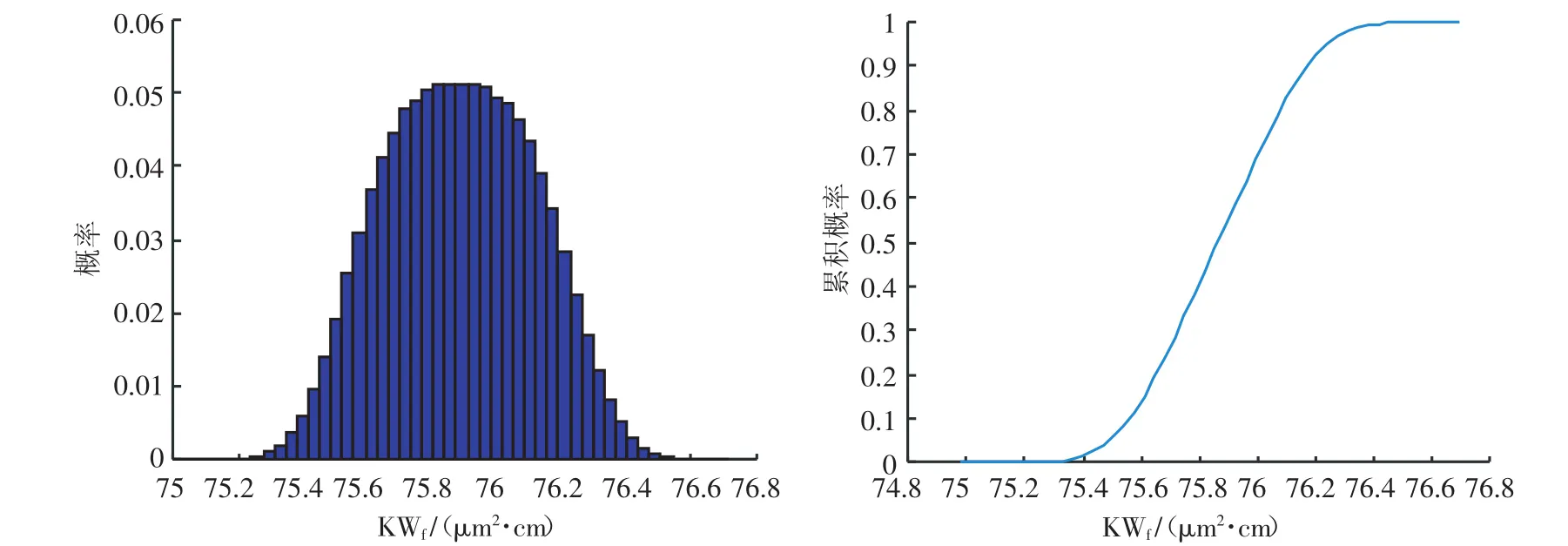
图5 试验次数为100万次的导流能力计算结果

（2）分析了蒙特卡洛方法实现不确定度评定的实施步骤，并推导了概率密度函数对应的随机变量的获取公式。

（3）支撑剂充填层短期导流能力测量不确定度评定结果表明，试验次数在10万～100万次，采用蒙特卡洛方法计算出的估计值和标准不确定度结果稳定，试验次数越大，概率对称的95%的包含区间越小，精确度越高。

［1]黄美发，景晖，匡兵，等.基于拟蒙特卡罗方法的测量不确定度评定［J］.仪器仪表学报，2009，（1）：120-125.

［2]刘建坤，朱家平，郑荣华.测量不确定度评定研究现状及进展［J］.现代科学仪器，2013，10（5）：12.

［3]CNAS-CL07.测量不确定度的要求［S］.中国合格评定国家认可委员会，2011.

［4]邱鸣霞.测量不确定度的分析及应用［J］.黑龙江科技信息，2008，（26）：10.

［5]JJF1059.2-2012.用蒙特卡洛法评定测量不确定度［S］.国家质量监督检验检疫总局，2012.

［6]陈怀艳，曹芸，韩洁，等.基于蒙特卡罗法的测量不确定度评定［J］.电子测量与仪器学报，2011，25（4）：301-308.

［7]Willink R.On using the Monte Carlo method to calculate uncertainty intervals［J］.Metrologia，2006，43（6）：L39.

［8]Esward T J，de Ginestous A，Harris P M，et al.A Monte Carlo method for uncertainty evaluation implemented on a distributed computing system［J］.Metrologia，2007，44（5）：319.

［9]Crowder S V，Moyer R D.A two-stage Monte Carlo approach to the expression of uncertainty with non-linear measurement equation and small sample size［J］.Metrologia，2005，43（1）：34.

［10]Hall B D.Monte Carlo uncertainty calculations with smallsample estimates of complex quantities［J］.Metrologia，2006，43（3）：220.

［11]Fernández M S，Calderón J A，Díez P B.Implementation in MATLAB of the adaptive Monte Carlo method for the evaluation of measurement uncertainties［J］.Accreditation and Quality Assurance，2009，14（2）：95-106.

［12]祖先锋，毛健人，蒋志文.基于自助法仿真的不确定度抽样反分析方法研究［J］.计算机应用与软件，2011，28（6）：215-217.

［13]Wang S，Chen X，Yang Q.Evaluation of measurement uncertainty based on Bayesian information fusion:Sixth International Symposium on Precision Mechanical Measurements［C］.International Society for Optics and Photonics，2013.

［14]高玉英.基于贝叶斯理论的动态不确定度评定方法的研究［D］.合肥：合肥工业大学，2007.

［15]Li J H，Tong R S，Cao S S.Analysis of Uncertainty in Standard Metal Tank Volume Verification with Monte Carlo Method:Advanced Materials Research［C］.Trans Tech Publ，2013.

Evaluation of uncertainty in measurement based on Monte-Carlo method

TAO Zuwen
（Downhole Operation Branch of Sinopec Southwest Petroleum Engineering Company，Deyang Sichuan 618000，China）

When the measuring mathematical model and the partial derivatives are too difficult to get,Monte-Carlo method is applicable to a single output and input can be approximated to any model probability density function.To further investigate the Monte-Carlo method in the evaluation of measurement uncertainty of the application,the paper analyzes the implementation steps of uncertainty evaluation,and derive the formula of random variables corresponding to its probability density.Example show that trials between one hundred thousand to one million times,the result of using the Monte-Carlo method to calculate the estimated value and standard uncertainty are stable.When the trials number are larger,the interval containing of probability symmetrical of 95%,and the accuracy is higher.

Monte-Carlo method；hydraulic fracturing；ceramic proppant；flow conductivity；measurement uncertainty

TE312

A

1673-5285（2017）09-0067-06

10.3969/j.issn.1673-5285.2017.09.017

2017－08-04

陶祖文，男（1989-），助理工程师，毕业于西南石油大学，主要从事石油工程现场应用及科研工作。