基于双层优化模型的多能互补微网储能优化配置

郑恩泽， 顾洁， 刘波， 卢海勇

(1.上海交通大学 电子信息与电气工程学院，上海 200240;2.上海电力设计院有限公司，上海 200240)

基于双层优化模型的多能互补微网储能优化配置

郑恩泽1， 顾洁1， 刘波2， 卢海勇2

(1.上海交通大学 电子信息与电气工程学院，上海 200240;2.上海电力设计院有限公司，上海 200240)

在多能互补微网系统中，为优化储能装置在不同运行状态下的容量配置，建立了同时考虑离网及并网运行状态的储能配置双层优化模型，采用考虑极值变异的混合型粒子群算法求解，获得了储能装置并、离网状态的协调优化配置方案。算例验证结果表明，求解得到的储能优化配置结果比传统单层优化模型更优，具有较快的收敛速度和较好的计算精度。研究结果为微网储能优化配置策略提供了参考。

多能互补微网；储能优化配置；离网运行状态；并网运行状态；双层优化；粒子群算法

Abstract: To optimize capacity configuration of energy storage devices in different operating status in multi-energy complementary micro-grids, we establish a bi-level optimization model for energy storage configuration which takes into account the off-grid and grid-connected operating states at the same time. By using the hybrid particle swarm algorithm with extremum mutation to calculate the model, we obtain a coordinated configuration scheme of such devices for both off-grid and grid-connected states. Results of example verification indicate that the optimal configuration obtained through solution of the model is more excellent than that of the traditional single-level model, and the algorithm has a fast convergence rate and good calculation accuracy. Results of the research work provide a reference for the optimal configuration of micro-grid energy storage.

Keywords: multi-energy complementary micro-grid; optimal configuration of energy storage; off-grid operating state; grid-connected operating state; bi-level optimization; particle swarm algorithm

0 引 言

随着我国经济发展，传统经济发展方式的能源利用效率低、污染严重等问题越发明显。多能互补微网系统(以下简称微网)将多种分布式能源、负荷、储能元件结合在一起，实现了冷热电联产。然而微源出力的不确定性、微网的运行状态切换过程也给系统的稳定运行及其电能质量造成了很大影响[1]。储能装置的引入有助于优化微源配置，降低装机及发电成本，提高电力系统设备的利用效率；有助于提高系统运行的稳定性[2]。

国内外针对微网储能优化配置问题开展了大量研究。主要从削峰填谷、经济运行等方面对储能配置进行优化。现有文献以经济调度[3]、弥补风电预测误差[4]等目标，对储能优化配置进行研究。但现有研究大多将微网的并、离网运行状态割裂开来进行考虑，建立储能优化配置模型[5]，缺乏同时考虑离网和并网运行状态需求的储能优化配置研究，优化结果难以同时满足不同运行状态下对储能装置容量的需求。

本文基于双层优化模型理论，建立综合考虑离网和并网运行状态的微网储能优化配置模型。以离网运行状态下的储能配置优化作为上层优化目标，以并网运行状态下系统运行优化为目标构建下层模型，通过迭代得到储能配置的优化结果，以考虑极值变异的混合型粒子群算法对模型进行求解。通过算例验证模型的有效性。

1 多能互补微网系统储能配置的双层优化模型

本文综合考虑微网离网状态下的储能优化配置及并网状态下的运行优化，目标函数包括离网运行状态下的配置成本及并网运行状态下的运行成本和环保成本,并将此问题转化为双层优化问题。图1为微网结构与能流示意，微网中包括燃气轮机、电制冷机、吸收式制冷机、余热锅炉、燃气锅炉、蓄冷设备、储热设备及储能设备。

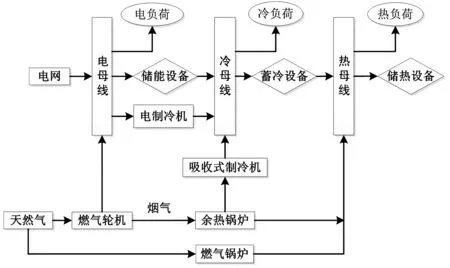
图1 微网结构示意图

1.1 双层优化理论简介

双层优化问题基本结构为：上层优化确定最优解，下层优化在上层模型的基础上确定最优解取值，然后将下层优化结果返回到上层，通过迭代得到最优解及其对应的最优值。其数学模型可以表示为：

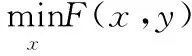
st.x∈X={x:H(x)≤0},

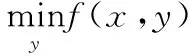
st.g(x,y)≤0，y∈Y={y:G(y)≤0}

(1)

式中x为上层优化的决策变量，F(x,y)为上层优化模型的目标函数，X为上层优化模型中决策变量的可行域，H(x)为上层优化模型中决策变量x满足的约束；y为下层优化模型的决策变量，Y为下层优化模型中决策变量的可行域，g(x,y)、G(y)分别为下层优化模型中的决策变量y满足的约束。

1.2 多能互补微网系统储能配置的上层优化模型

以离网状态下的微网储能配置的经济性为目标，考虑最大出力功率约束及爬坡率约束，构建上层优化模型。

1.2.1目标函数

综合考虑离网运行状态下储能设备的年平均化成本与并网运行状态下的优化目标归一化后通过线性加权的方式作为目标函数，表示如下：

minF=ρ1·CBSE+ρ2·f

(2)

CBSE=(Civ+Cwe)·kde·n

(3)

式中CBSE为储能装置年平均化成本，单位为元；Civ为储能装置的投资成本，单位为元；Cwe为单位储能装置的维护成本；kde为储能装置的年折旧系数；n为储能系统中蓄电池组的个数；f为下层优化模型目标函数的适应值，受上层决策变量影响；ρ1、ρ2为权重系数。

1.2.2约束条件

建立微网离网状态下储能优化配置模型时所考虑的约束条件。如下所示：

(4)

式中Pload，max为微网最大负荷，单位为 kW；PGT,max为燃气轮机装机容量，单位为 kW；PBSE,max为储能装置最大出力功率，单位为kW；ΔPU为上升率限制，单位为kW/h；ΔPD为下降率限制，单位为kW/h。

1.3 多能互补微网系统储能配置的下层优化模型

以并网状态下的微网经济性和环保性为目标构建下层优化模型。然后利用基于线性加权思想的随机加权法对双目标问题进行单目标化处理。

1.3.1目标函数

微网运行优化模型的优化目标包括经济性和环保性。本文采取随机加权法，给每个目标随机分配权重，将其单目标化，寻找目标函数的最优解。微网经济性成本包括微源的运行成本、成本、微源设备的启停成本、从电网购电成本。为满足可持续发展要求，还应该考虑到微网环保性。微网在运行时的主要污染物中CO2占比最大，因此本文重点考虑该部分气体排放物的排放，利用CO2排放系数将微网电力消耗量和天然气消耗量转化为CO2排放量。采用随机加权法后的多目标优化函数可表示为：

f=k1f1+k2f2

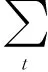
(5)

式中k1、k2均为随机数，0≤k1≤1，0≤k2≤1且k1+k2=1。Cr为微源的运行成本，单位为元/kWh；Cm为微源的运行维护成本，单位为元/kWh；Cs为微源的启停成本，单位为元/次；MB为微网向电网购电的价格，单位为元/kWh。K(t)为微源的启停状态(0表示停，1表示启)；P(t)为每种微源输出功率，单位为kW；Pgrid(t)为微网向电网购电功率，单位为kW。Fi为微网设备单位发电量对应的污染物排放量，单位为kg/kWh；Pgi为微网设备发电功率，单位为kW。

1.3.2约束条件

(1)功率平衡约束

微网功率平衡约束包括冷、热、电功率平衡约束：

(6)

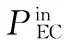
(2)出力功率约束

(7)

式中Pgrid,max表示从电网购电功率上限；Ki(t)为第i个单元的状态情况(1表示运行，0表示停运)；Pi,min、Pi,max分别表示第i个单元的出力功率上下限，单位为kW；Pi(t)表示第i个单元出力功率，单位为kW。

(3)储能设备储能约束

Qi,min≤Qi≤Qi,max

(8)

式中Qi,max、Qi,min分别表示各储能设备单元的储能能量上、下限值，单位为kWh。

(4)可控型出力设备最短连续运行时间和最短连续停运时间约束

(9)

式中Ti_on(t-1)、Ti_off(t-1)分别为t-1时刻第i台微源的连续运行、停运时间，单位为h；MRTi、MSTi为微源最小连续运行、停运时间，单位为h。

(5)可控型出力设备功率爬坡率约束

(10)

式中ΔPU为上升率限制，单位为kW/h；ΔPD为下降率限制，单位为kW/h。

2 求解双层优化模型的粒子群优化算法

2.1 考虑极值变异的混合型粒子群算法

本文建立的双层优化模型的下层模型对收敛精度要求较高，而且整体模型结构复杂。为兼顾算法的收敛速度以及收敛精度，采用考虑极值变异的混合型粒子群算法，在搜寻前期采用极值变异的粒子群算法以增大粒子跳出局部最优陷阱的能力，并在算法后期采用全局优化以改善算法收敛的速度。本文所应用的粒子群算法对迭代过程中的粒子运动惯性权重、学习因子进行了修改，兼顾算法前期和算法后期的收敛情况；弱化粒子寻找最优解过程中的速度概念，突出位置概念；增加极值变异因子，增大粒子跳出局部最优的能力，提高算法全局寻优能力。

本文采取的粒子群算法公式为：

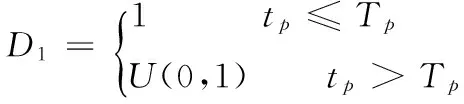
(11)

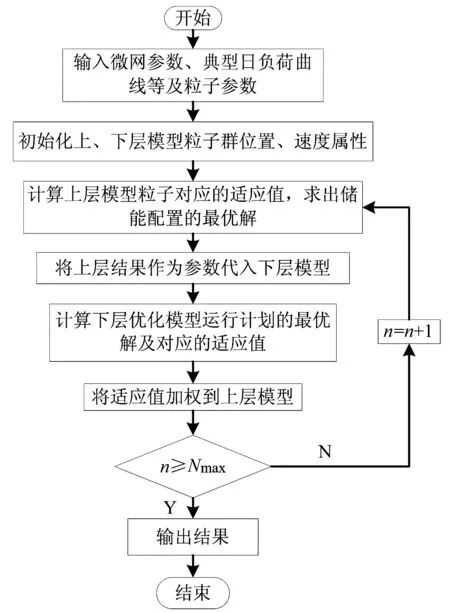
图2 储能配置的双层优化模型求解流程

式中D1、D2分别为粒子的个体极值和群体极值变异因子；tp、Tp分别为粒子自身极值停滞次数和停滞次数阈值；tg、Tg分别为粒子群体极值停滞次数和停滞次数阈值。

2.2 储能配置的双层优化模型求解流程

采用考虑极值变异的混合型粒子群算法求解本文提出的双层优化模型的主要步骤如图2所示。

3 算例分析

3.1 算例参数

针对本文提出的双层优化模型，选取某地微网，选取某铅蓄电池作为储能元件。以该系统典型日各类负荷曲线作为并网运行需求，进行储能优化配置。该地实施的电价机制为每天7-21时0.977元/kWh，在22-6时为0.487元/kWh。天然气价格为2.5元/m3，天然气热值取为9.78 kWh/m3[6]。该微网冷、热、电负荷曲线如图3所示。

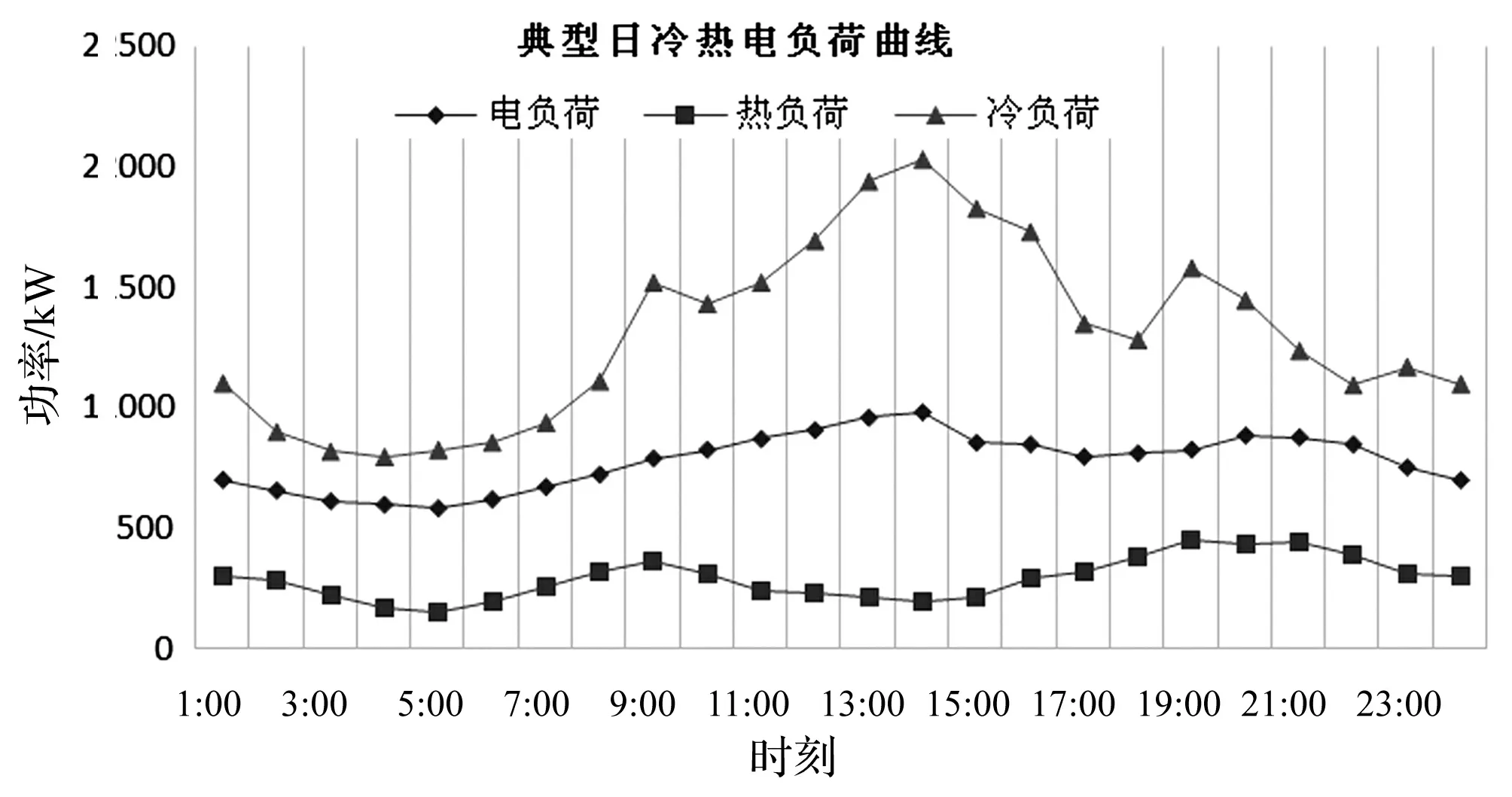
图3 典型日冷热电负荷曲线

本文选取设备参数见表1、表2所示，表3为备选的蓄电池参数。

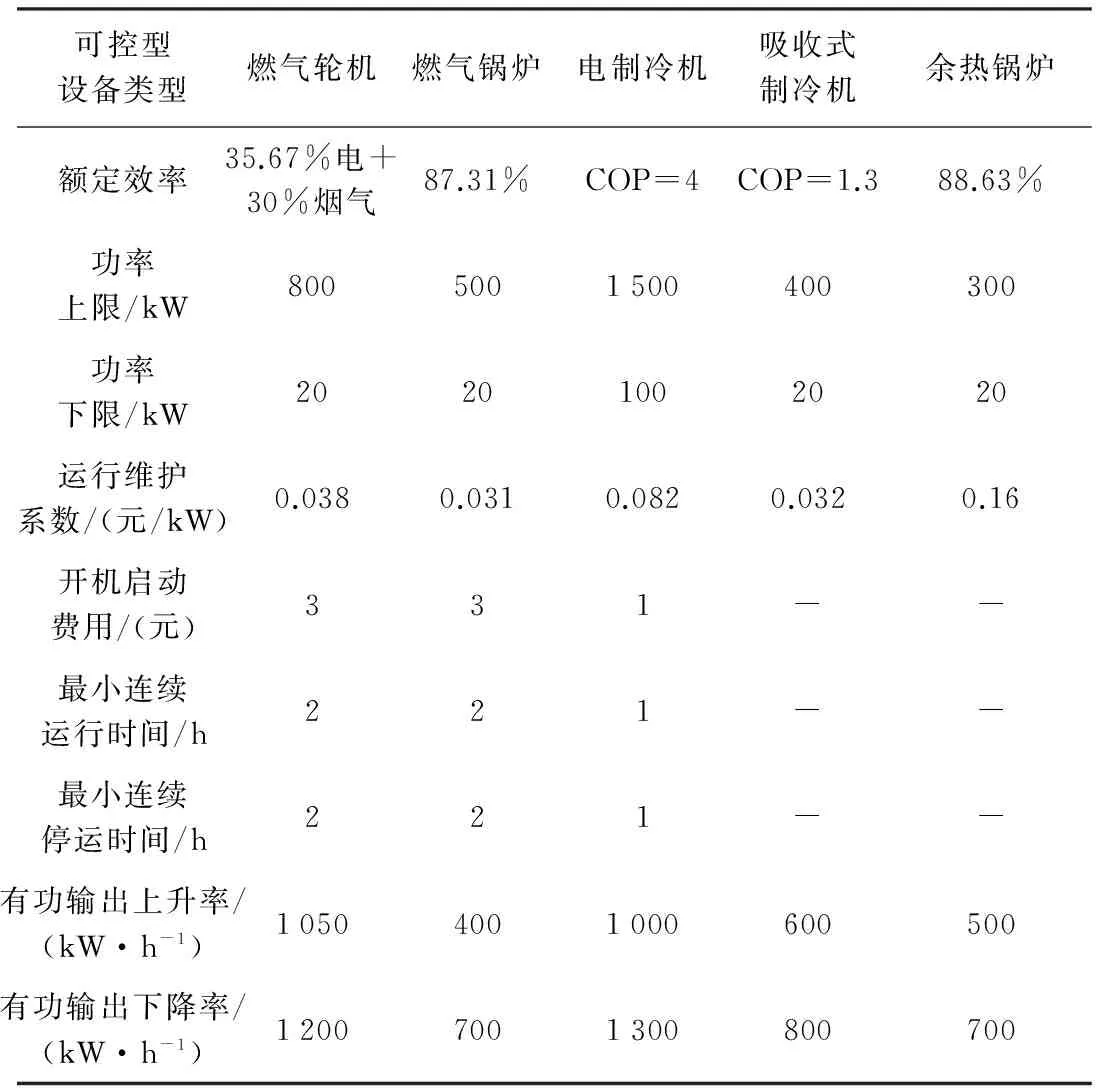
表1 联供系统设备主要参数

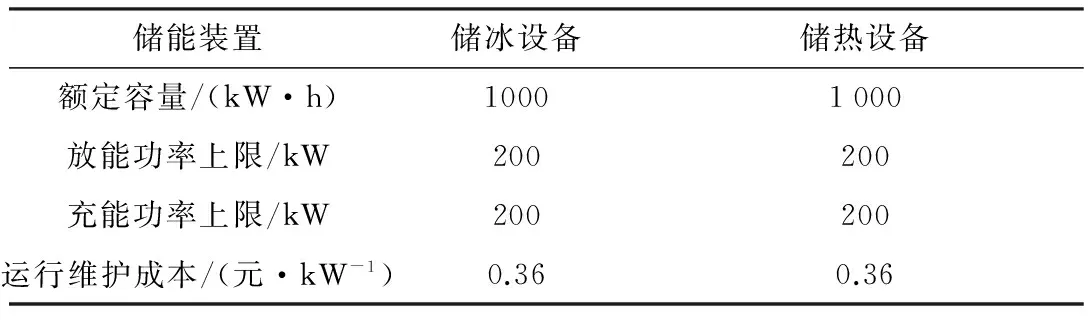
表2 分布式储能设备参数

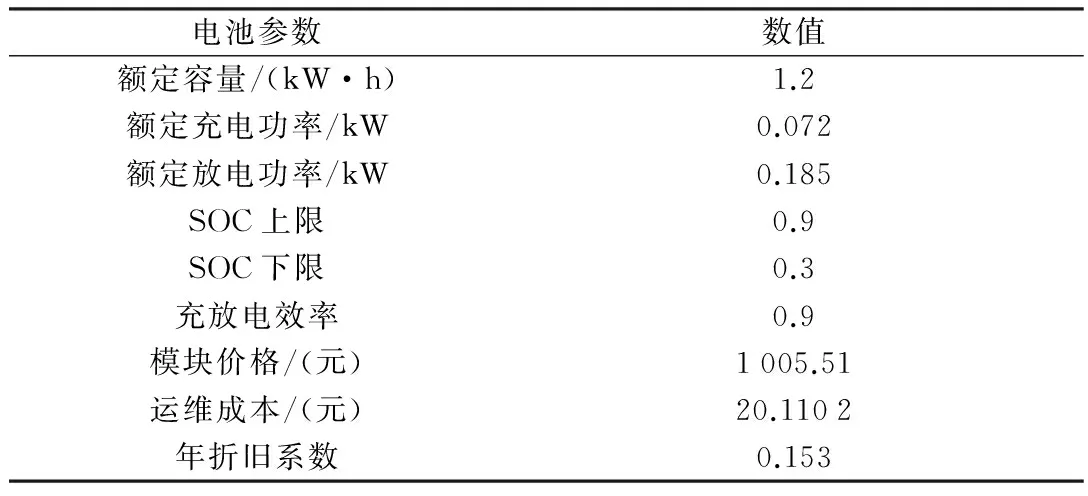
表3 储能设备参数

3.2 算例结果及分析

采用本文建立的模型对算例中微网储能配置进行优化。粒子数设为100，迭代次数设为2 000，得到双层优化模型适应值结果如表4所示。作为对比，计算出只考虑离网运行状态模型适应值以及在此配置下并网运行状态适应值。可以看出，双层模型得到的储能装置装机成本和运行成本及环境成本之和较小。

表4 双层模型优化计算结果

粒子群的适应度收敛计算结果如表5所示，可以看出，相比于基本粒子群算法，本文应用的考虑极值变异的混合型粒子群算法收敛速度较快，收敛性较好。

表5 不同粒子群算法收敛结果

4 结束语

本文基于微网并、离网两种运行状态建立其储能装置的双层优化配置模型。应用考虑极值变异的混合型粒子群算法对模型进行求解。并且选取了某地的微网为算例，对提出的模型进行求解验证。

算例分析表明：

(1)相比于仅考虑一种运行状态的优化模型，本文应用的双层优化模型能够同时满足离网状态下的储能配置需求以及并网运行状态下的运行需求；

(2)本文提出的双层优化模型可以较好地对微网的储能配置进行优化，满足微网的配置需求；

(3)所采用的考虑极值变异的混合型粒子群算法具有较好的收敛性，可应用于求解本文提出的双层优化模型，并且优化结果较好。

[1] 杨秀，陈洁，朱兰，等. 基于经济调度的微网储能优化配置 [J]. 电力系统保护与控制,2013,41(1):53-60.

[2] 江润洲，邱晓燕，陈光堂. 风电场混合储能系统优化配置方法 [J]. 电力系统及其自动化学报,2015,27(1):37-42,48.

[3] 刘舒，李正力，王翼，等. 含分布式发电的微电网中储能装置容量优化配置 [J]. 电力系统保护与控制,2016,44(3):78-84.

[4] 丁明，徐宁舟，毕锐. 用于平抑可再生能源功率波动的储能电站建模及评价 [J]. 电力系统自动化,2011,35(2):66-72.

[5] 李成，叶建华. 微网系统中储能优化配置研究 [J]. 低压电器,2013,55(22):23-26.

[6] 陈云，汤放奇，刘阳升，等. 分布式冷热电多联供系统的经济运行 [J]. 电力科学与技术学报,2013,28(1):56-62.

Optimal Configuration of Energy Storage for Multi-energy Complementary Micro-grids Based on a Bi-level Optimization Model

Zheng Enze1, Gu Jie1, Liu Bo2, Lu Haiyong2

(1.College ofElectronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China，2. Shanghai Electric Power Design Institute Co., Ltd., Shanghai 200240, China)

10.3969/j.issn.1000-3886.2017.03.015

TM761

A

1000-3886(2017)03-0045-04

定稿日期: 2017-01-11

郑恩泽(1992-)，男，吉林人，硕士生，专业：电气工程系。