基于提升小波的时间序列分析法的电力负荷预测

张帆，张峰，张士文

(上海交通大学 电子信息与电气工程学院，上海 200240)

基于提升小波的时间序列分析法的电力负荷预测

张帆，张峰，张士文

(上海交通大学 电子信息与电气工程学院，上海 200240)

为了合理分配电能和规划电网运行，需要对居民小区电力负荷进行精确预测。提出了一种基于提升小波的时间序列分析法进行电力负荷预测，采用提升小波对居民小区电力负荷进行主要特征量提取，避免了用电量数据随机性和波动性的干扰；运用时间序列法对经过提升小波去噪后的电力负荷序列，求取自相关和偏相关系数，确立相应数学模型，预测未来时刻的用电量。最后，利用上海嘉定某小区的历史负荷大数据进行了比较和分析，验证了方法的有效性。

电力负荷预测；提升小波；时间序列法；数学模型；大数据

Abstract: For the purpose of rational distribution of electric energy and planning of power grid operation, it is necessary to make precise forecasting on power load of residential quarters. Here, we propose a time series analysis method based on lifting wavelet to make power load forecasting. Lifting wavelet is used to extract main characteristic quantities of power load in residential quarters, thus avoiding interference from randomness and volatility which occur if electricity data is used. The time series method is used to calculate autocorrelation and partial correlation coefficient of the power load series which has been denoised through lifting wavelet, establish corresponding mathematical models and forecast future electricity consumption. Finally, comparison and analysis is made by use of the big data of past load of a certain residential quarter in Jiading District, Shanghai, and the effectiveness of the proposed method is verified.

Keywords: power load forecasting； lifting wavelet； time series method； mathematical model； big data

0 引 言

为响应深入改革政策，我国电力行业市场化正在加速步伐。作为电力系统最主要的任务之一，为用户提供优质稳定的电能成为了电力行业专家们研究关注的焦点，这种行业背景下的负荷预测则显得尤为重要。电力部门投资电力项目，规划输配电方式都以负荷预测的结果作为主要参考依据，使得负荷预测的精度直接影响到电力系统运营的效率和经济效益[1]。

精准的负荷预测离不开科学的计算和分析方法，随着对于预测精度的要求日益提高，衍生出了一些负荷预测的方法[2-4]。

(1)提升小波变换，作为第二代小波变换，相较第一代小波变换，具有运算简便，适用范围广的优点，能够更加稳定高效地去除包含在负荷波形中的高频噪音。

(2)灰度预测法，适用于含有不确定因素的系统，对系统因素之间发展趋势的相异程度进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。

(3)神经网络法，是由大量简单的处理单元(神经元)互相连接而形成的复杂网络系统,能够分步存储和处理数据，具有很强的自我学习能力，适用于复杂的非线性系统。

(4)时间序列法，是通过曲线拟合和参数估计建立数学模型的预测方法，对于按照时间排列的数据序列具有很强的处理计算能力。

然而随着社会经济的高速发展，消费结构和消费观念的变化，使得影响负荷变化的因素越来越多，电力负荷的预测也变得越来越难以掌控，多种传统预测方法也逐渐暴露出了其局限性，需要更深入地研究，改进创新方法，达到精确预测的目的[4]527。

本文提出了一种基于提升小波的时间序列分析法进行电力负荷预测。该方法结合了提升小波和时间序列两种传统方法各自的算法优势，可以提高对电力负荷预测的精度。本文还引入了上海市嘉定某小区的历史负荷大数据，通过比较和分析，验证了该预测方法的有效性。

1 提升小波变换

W.Sweldens通过研究发现小波变换(Wavelet Transform，WT)对于基于傅里叶分解频域内的复杂计算过于依赖，导致其难以对一些随机性强，波动性大的信号进行分析处理，且难以用硬件实现[5]。因此他提出一种新的更为高效实用的小波变换方法——提升小波变换(Lifting Wavelet Transform，LWT)，这种提升算法可以独立地基于空域，无需经过傅里叶变换，直接在原波形的基础上进行分解运算，其逆变换也可直接通过反转正变换得到，大幅降低了运算复杂性[6]。此外，经过Daubechies等人证明，所有可以通过马拉特(Mallat)算法实现的小波都可以用提升算法实现，即其适用范围相比普通小波变换更广。因此这种提升变换对于要求快速运算，实时操作的电力系统来说十分重要。

提升小波算法主要包含分裂(Split)、预测(Predict)、更新(Update)。假设一个输入小波X[n]，通过以下三个步骤来获得该小波经过提升算法后的形式[7]。

1)分裂

(1)

2)预测

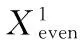
(2)

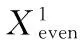
(3)

3)更新

(4)

X1(n)为经过修正后的序列，也是X(n)的一条低频拟合曲线，U为更新算子，可取多种函数，例如：

(5)

经过这样的小波提升变换，原始信号X(n)最终被分解成低频圆滑信号X1(n)和高频噪音d1(n),在此基础上再对X1(n)重复以上三个步骤，分解出X2(n)、X3(n)、X4(n)…和d2(n)、d3(n)、d4(n)…，分解次数越多，高频噪音过滤的则越彻底。

显而易见以上所有运算过程都是可逆的，因此提升小波的逆变换也只需将之前的运算反转即可得到。在已知X1(n)和d1(n)的情况下，可通过如下反变换得到原序列X(n)[8]。

(6)

2 时间序列法

时间序列法(Time Series Analysis Method，TSAM)就是利用已知数据依照时间排列并具有历史延续性的特性，对相关数据进行数学建模进而预测序列未来变化趋势的方法。美国专家学者George Box和英国统计学专家Gwilym Jenkins于1968年首次提出时间序列法，这种方法通过分析已知数据的变化规律，进而建立数学模型，最后将时间信息代入该数学模型达到对未来时刻序列数值的预测计算[9]。主要原理如下：

记按照相等时间间隔排列的时间序列数据为Xn，n∈N，通过时间序列法的相关公式计算该时间序列X1,X2,…,Xn的自相关函数τk和偏相关函数βkk并判断它们的“拖尾性”与“截尾性”。如若以上两种性质皆不具备，则说明该序列为非平稳序列，即序列中包含的随机因素较多，影响对于序列具有何种规律性的判断，需要对其经过差分运算来消除随机因素的干扰。

dXn=[dX1,dX2,…,dXn]

(7)

d表示差分运算的阶数，序列经过一阶差分运算后继续计算其自相关，偏相关函数，若仍为非平稳序列，则需再次经过有限次的差分运算直至序列平稳并得出自相关，偏相关函数的“拖尾”，“截尾”性为止。

根据函数性质选择相应的数学模型，选择准则如表1所示。

表1 模型选择准则

选出最适合的数学模型后，建立相应的模型结构表达式，通过参数估计计算求解出表达式中的各个未知参数的估计值，最终得到数据序列Xn的完整数学模型表达式。

最后对比时间序列法的预测值与实际值，经过显著性检验确认其可行性。如若可行，便可用其来预测之后更长一段时间内的电力负荷，如若不可行，则重新对模型中的参数进行估计，再次通过显著性检验直到其可行为止[10]。

3 提升小波的时间序列分析法

我国城市的居民小区电力负荷检测地点环境复杂，周围可能安装有变压器等大型设备，会对电力负荷的实际值产生高频噪音干扰，破坏数据的可靠性。为确保负荷预测的精度，本文提出了提升小波的时间序列分析法(Time Series Analysis Method of Lifting Wavelet Transform，LWT-TSAM)。在对用于预测的历史负荷数据进行处理之前，先去除包含在序列中的噪音元素。

由于居民小区的用电消耗具有较强社会人为性，使得负荷序列包含规律性的同时也具有较强的波动性与随机性，传统的小波变换难以有效去除包含在其中的高频噪音。

新一代小波变换——提升小波变换(LWT)具有适用小波范围广，对波动大，随机性大的序列处理能力强，计算过程和硬件实现简便等优点，对于居民小区电力负荷的去噪十分适合。

记第n年第m小时的电力负荷消耗为Wn,m，(m∈[1,876])，则历史用电量序列为：

W=[Wn-1,8760,Wn-1,8759,…,Wn-1,1,

Wn-2,8760,Wn-2,8759,…,Wn-2,1,…]

(8)

将式8分解成奇偶两个子序列如式(9)所示。

SplitW=[Wodd,Weven]

Wodd=[Wn-1,8759,Wn-1,8757,…]

(9)

Weven=[Wn-1,8760,Wn-1,8758,…]

经提升小波预测及更新运算后得到低频负荷序列如式(10)所示。

(10)

任取低频序列W′中n个连续元素构成一个子序列Wn=[W1,W2,…,Wn]并计算其均值函数估计如式(11)所示。

(11)

进而得到其协方差估计计算式，如式(12)所示。

(12)

最终可通过式(13)计算自相关函数τk的估计值。

(13)

利用已求得的自相关函数可代入递推式(14)继续计算偏相关函数βkk的估计值。

(14)

将用模型预测出的结果与实际值对比，经过显著性检验验证模型可行性，如若未通过检验则需重新选取随机子序列Wn=[W1,W2,…,Wn]，重复以上步骤计算出新的参数估计值，直到序列数学模型可靠为止。

在用该模型预测一段时间的电力负荷后，由于历史负荷数据得到更新，为保证之后预测的精度，可代入更新后的历史负荷数据重复以上步骤，进行更加长远地预测。

提升小波的时间序列分析法的预测系统流程如图1所示。

图1 电力负荷预测系统框架

4 实例分析及结果展示

4.1 实例分析简介

选用上海市嘉定某居民小区2010至2013年精确至小时级的用电负荷数据作为研究分析的大数据来源。将2010至2012年的用电负荷作为历史数据，经提升小波去噪后利用时间序列法建立数学模型先预测2013年第一个月的用电负荷，将结果与实际负荷值经显著性检验对比，修正参数后再预测第二，三个月。由此得出2013年第一季度的用电负荷预测值。接着代入2010至2013年三月的历史负荷数据，重新建立数学模型求取2013年第二季度的负荷预测值，以此类推直至得出2013年全年的电力负荷预测值。

本文采用2012年大数据作为历史数据样本，展示所提出算法的应用情况。采用2012年负荷数据经提升小波去噪，以及差分算法平稳化后的波形并进行分析计算，预测2013年的电力负荷情况，并采用2013年的真实数据作为验证。在文中对于历史数据的分析和未来电力负荷的预测，分别比较了时间序列法(TSAM)和基于提升小波的时间序列法(LWT-TSAM)两种方法的预测结果。

4.2 预测结果与分析

4.2.1时间序列法的预测结果

首先验证未经提升小波去噪进行数据处理，仅用时间序列法进行预测的结果。

图2 2012年电力负荷实测值

为方便清晰展示序列平稳化的结果，将经差分算法处理前后的2012年历史负荷数据，按照每24小时相加得出日负荷序列。差分算法处理前的2012年负荷序列如图2所示。

图3 平稳化的2012年电力负荷序列

由于序列包含随机因素较多，需对序列进行差分运算使得其足够平稳从而显现出应有的规律性。经过3次差分运算后的2012年负荷序列如图3所示。

图4 TSAM的预测与实际负荷值

图5 TSAM的百分比误差分布

通过式(13)，(14)计算序列的自相关、偏相关系数，判断出二者皆具备拖尾性，经模型选择准则判断，选取ARMA(p,q)数学模型对序列进行拟合，求取参数并进行显著性检验。为清晰对比预测与实际结果，将序列按照一周168小时累加，得出2013年的周负荷序列如图4所示。

时间序列法的预测结果的相对误差分布如图5所示。

4.2.2基于提升小波的时间序列法预测

图6 2012年8760小时电力负荷序列

图7 经LWT处理后的电力负荷序列

图8 2012年负荷序列中的高频噪音

采用提升小波方法可以对历史负荷数据进行去噪，获得电力负荷序列的低频部分。选用上海市嘉定某居民小区2012年精确至小时级的负荷序列如图6所示，其经过提升小波4层分解后的低频序列如图7所示，所去除掉的高频噪音序列如图8所示。

将去噪后的序列运用时间序列法进行数学建模，预测出2013年全年的电力负荷与实际值对比波形图如图9所示，预测结果的相对误差分析如图10所示。

图9 LWT-TSAM的预测与实际负荷值

图10 LWT-TSAM的百分比误差分布

以上列举方法的预测结果如表2所示。

表2 预测方法汇总表

5 结束语

本文提出了一种基于提升小波的时间序列法，可进行居民小区电力负荷预测。通过理论分析、数学建模、大数据处理、实例验证和比较分析，可以得出以下结论：

(1)针对居民用电负荷的随机波动特性，利用提升小波对收集来的负荷序列进行4层分解，去除了包含在序列中的由于电磁干扰等客观因素造成的高频噪音，降低序列的随机性，可以有效地提升预测的精度。

(2)时间序列法作为一种传统的数学预测方法，在电力负荷的预测领域同样具有很高的实用性和可靠性，采用时间序列法反映包含在低频负荷序列中的规律，并应用相应的数学模型进行拟合，进而代入时间序列数据，可以计算获得未来时刻的电力负荷，进行电力负荷预测。

(3)选用上海市嘉定某居民小区2010至2013年精确至小时级的用电负荷数据进行大数据分析和研究。采用2012年大数据作为历史数据样本，运用基于提升小波的时间序列法进行分析和计算，预测了2013年的电力负荷情况，并与2013年的真实数据进行比较，验证了该方法的有效性。

[1] 廖旎焕，胡智宏，马莹莹，等. 电力系统短期负荷预测方法综述[J].电力系统保护与控制，2011，39(1)：147-152.

[2] 康重庆，夏清，刘梅. 电力系统负荷预测[M].北京：中国电力出版社，2007.

[3] 牛东晓，曹树华，卢建昌. 电力负荷预测技术及其应用 [M]. 北京: 中国电力出版社, 2009.

[4] 王德文，孙志伟. 电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报，2015，35(3)：527-537

[5] 潘泉，张磊，孟晋丽，等. 小波滤波方法及应用[M].北京：清华大学出版社，2005.

[6] 葛哲学，沙威. 小波分析理论与MATLAB R2007实现[M].北京：电子工业出版社，2007.

[7] 潘泉，孟晋丽，张磊，等. 小波滤波方法及应用[J]．电子与信息学报，2007，29(1)：236-242

[8] 李霄. 基于提升小波和最小二乘向量机的风电功率预测[D].上海:上海交通大学硕士论文，2015.

[9] 张超. 基于时间序列法超短期负荷预测改进方法的研究[D].辽宁:辽宁工业大学硕士学位论文，2015.

[10] 朱晓荣，刘艳萍. 基于稳健估计时间序列法的风功率预测[J].电力系统及其自动化学报，2012，24(3)：107-110.

Power Load Forecasting in the Time Series Analysis Method Based on Lifting Wavelet

Zhang Fan, Zhang Feng, Zhang Shiwen

(College of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

10.3969/j.issn.1000-3886.2017.03.022

TM714

A

1000-3886(2017)03-0072-05

定稿日期: 2016-10-06

张帆(1991-)，男，安徽濉溪人，上海交通大学电子信息与电气工程学院硕士生，研究方向电工理论。 张峰(1968-)，男，江苏人，博士，教授，博士生导师，从事电工理论与新技术、故障诊断与智能检测、现在轨道交通技术等。 张士文(1976-)，男，黑龙江人，硕士，讲师，从事电工理论与新技术、计算机控制技术、故障诊断、智能家居等。