基于价格博弈的需求侧管理智能控制系统研究

秦超，刘传清，陈龙，裴谦，卢双

(南京工程学院 电力工程学院，江苏 南京 210044)

基于价格博弈的需求侧管理智能控制系统研究

秦超，刘传清，陈龙，裴谦，卢双

(南京工程学院 电力工程学院，江苏 南京 210044)

在智能电网中，需求侧管理是优化资源利用的有效方法，供电公司可以通过采取合适的定价策略以改变用户的消费行为来调整负荷，从而使电力系统负荷峰均比最合理化，用户可根据电价信息规划自己的用电以降低用电费用。设计的智能控制系统具有双向通信功能，能够及时收集电力公司电价信息并及时发布用电计划，同时具有电力计量和智能用电分析功能，并分析了需求侧管理算法模型。最后给出了实验结果，表明可以大大降低用户消费，改善电力系统峰均比。

需求侧管理；智能控制系统；设备规划；价格博弈；峰均比

Abstract: In smart grids, DSM is an effective method to optimize resource utilization. The power company may adjust the load by adopting a suitable pricing strategy to shape users’ consuming behavior, thus achieving a most reasonable PAR for the power system load. Each user may schedule its power consumption according to price information so as to reduce its electricity payment. This paper designs a smart control system with bidirectional communication function which can timely collect price information of the power company and publish power scheduling and has the functions of power measurement and intelligent power consumption analysis. Furthermore, this paper makes an analysis on a DSM algorithm model. Finally, it gives experimental results which show that this method can significantly reduce users’ consumption and improve PAR of the electric power system.

Keywords: demand side management (DSM); intelligent control system; equipment scheduling; price game; peak-to-average ratio (PAR)

0 引 言

随着电动汽车、智能家居及楼宇的日益普及，使得参与主导电力系统运营的决策主体趋于多样化，在此情况下，如何确定各决策主体最佳策略从而平衡和优化电力系统有关各方利益是一项极具挑战性的课题，此种背景下，面向复杂主体多目标优化的博弈论完全有望成为攻克智能电网诸多关键难题的有力工具[1]。供电公司能控制和改变用户的消费，通过控制电价以减少峰均负荷率PAR(peak-to-average load ratio)。另一方面，辅助信息技术能使得消费者监视分时电量消费，以及市场电价的变化来保存电能或减少电费，将部分用电从峰值时间转到非峰值时间。供电公司采用合理的定价模式是控制和改变用户的消费有效的方法，比如我国曾使用的阶梯电价IBP(inclining block pricing)，使得电能被低收入者使用，以满足基本需要如照明或冷藏。但当要求消耗更高的电能时，例如空调或制热时，就会切换到更高的电价。供电公司还可以采取其他定价策略控制需求响应，如临界峰值定价CPP(critical-peak pricing)，分时电价TUP(time of use pricing)，实时电价RTP(real-time pricing)，日前定价DAP(day-ahead pricing)等。文献[2]设计了用户侧能量管理系统(U-EMS)原型，该系统可实现用电设备的功率采集、总用电量计算及用电设备的通断等基础功能。文献[3]提出一种具有监测设备用电状态和自动断电的相对独立的插座模型，并抽象出二元状态控制模型，在该控制模型与人机交互的基础上设计了智能控制算法使其成为一种相对独立的智能用电控制模块。该插座可以进行人机交互，能够记忆设备用电状态，并能够判断设备的用电状态，从而决定、实施设备的通、断功能，节约大量的待机功耗。文献[4]介绍的基于WiFi构建的智能家居控制系统，该系统采用PC主机和智能手机作为基本硬件平台，以实现智能家居控制系统。文献[5]提出可中断负荷属于需求侧响应中的激励响应，在文中的模型中，以最大化可中断负荷综合指标来确定可中断负荷用户，最终达削减峰值负荷的目的。以上文献都以用电控制为目的，并兼顾供电系统负荷均衡，由于缺乏交互，无法达到最优化。

本文采用博弈论策略设计一种智能控制系统以最优化需求响应，实现供电和用电效益最大化。供电公司通过实时定价激励消费者调整他们的消费行为，以使部分负荷从峰值时间转移到非峰值时间，实现峰均比最合理化。

1 系统模型

不失一般地假定系统由一个供电公司和多个用户构成，系统组成如图1所示。电力公司首先依据已有的信息预算接下来几个小时的电量需求，为不同时段设置了价格，并通过辅助数字通信网络，把价格发给用户。每一个用户根据电价信息调整自己的消费，即调整家庭各电器的最佳使用计划。

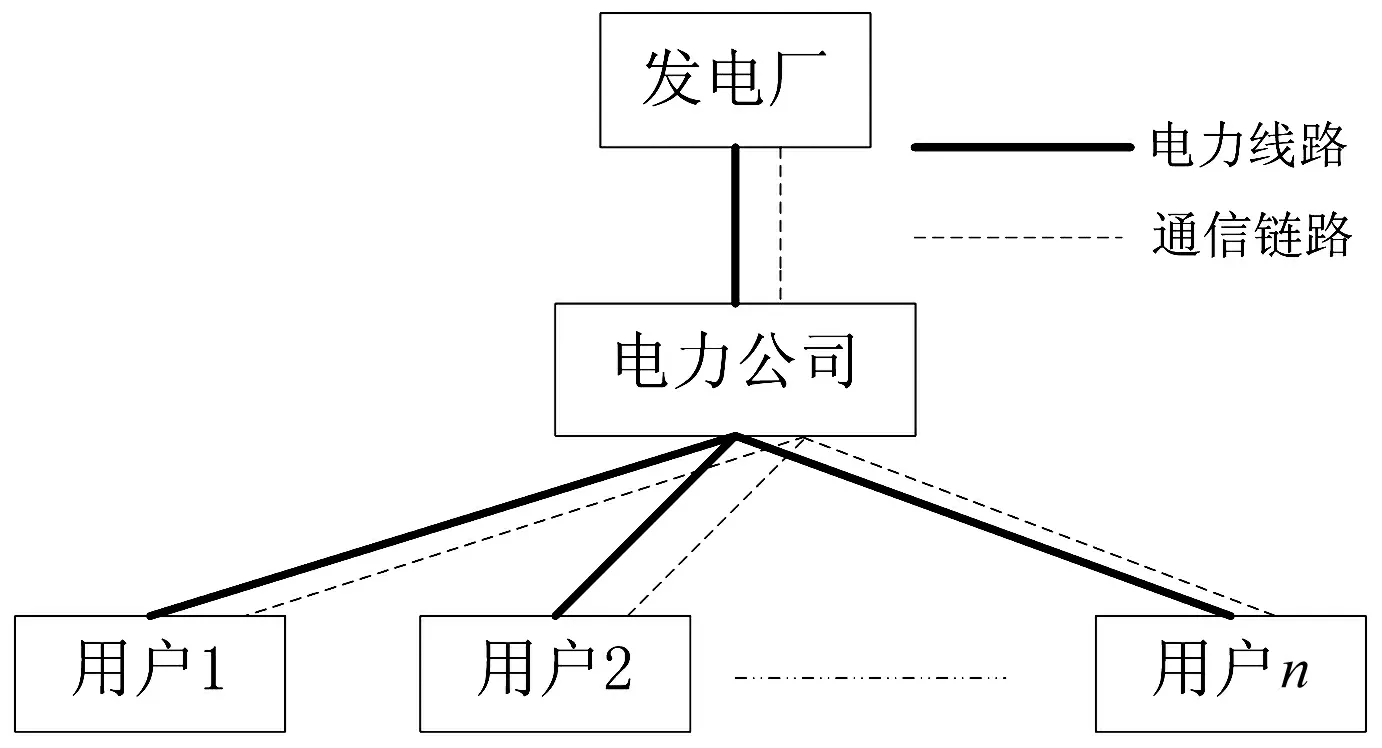
图1 电力系统供需结构图

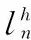
(1)

一天最大负荷为(日峰值)：

(2)

一天平均负荷为：

(3)

因此，电力系统的峰均比PAR表示为：

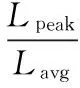
(4)

对于每个用户n∈N，用An表示家用电器集合，如电灯、电视、洗衣机、PHEV等等。对于每个家用设备a∈An，定义能量消耗计划矢量为：

(5)

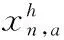
(6)

实际上，对于所有家用电器在不同时间h的消耗是不一样的。图2给出了智能调度器结构示意图，智能仪表(smart meter)里的规划任务(task of scheduler)决定了能耗矩阵Xn,a的最优选择(对设备a∈An)，以构建用户n的日负荷概况。

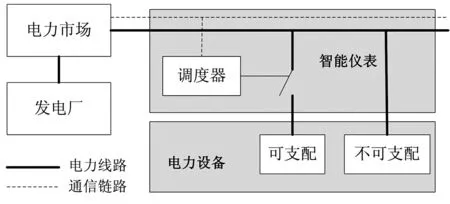
图2 智能调度器结构图

图3是智能控制系统的组成结构图。控制系统可以划分为6个部分组成：电力载波双向通信模块负责信息的双向传输；处理器和需求侧管理模块为单元的处理中心，是算法和管理中心，负责智能终端的控制与管理，以及电力计量存储分析等任务；无线WIFI实现智能家居的互联与无线管理；电力计量模块完成用电单元的电力计量；输出控制单元就是完成电器用电实时控制过程；开关电源为终端各模块提供电源。

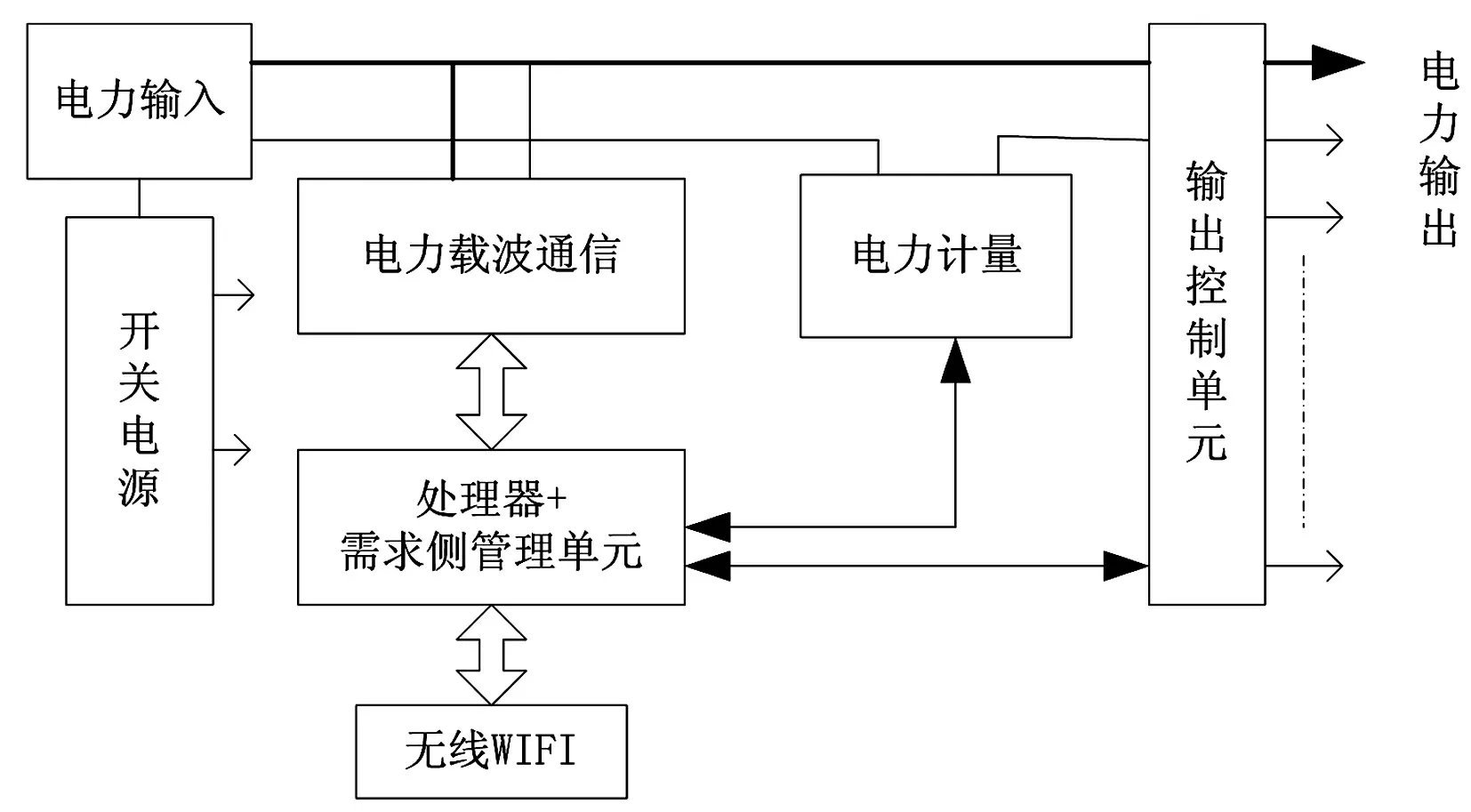
图3 智能控制系统组成结构图

2 价格博弈算法

对于每个用户n∈N，以及每台用电设备a∈An，先确定的日总消耗为En,a。注意这个规划目的不是改变能耗总量，而是为了系统的管理和调整。比如为了减少峰均比PAR或最小化能源消费。此例中，用户需要确定设备a∈An被规划的时间区间，设起始时间为αn,a∈H，结束时间为βn,a∈H，且αn,a≤βn,a。则：

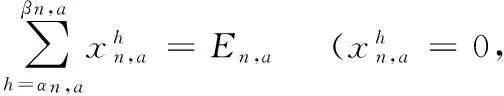
(7)

其中Hn,a={αn,a,…,βn,a}。对于每个用电设备，用户提供的时间区间需要大于等于需要结束操作的时间区间。在一天时间系统内所有设备总能耗等于所有设备的日能耗。即满足如下公式：

(8)

一般说来，有些设备的操作并非时间可调性，他们有着严格的能耗规划限制。如冰箱必须一直开着。此时αn,a=1，βn,a=24，如图3所示, 智能仪表里的调度器对于非可调家用电器，没有能耗规划。

博弈优化目标有两个：峰均比PAR最小化以及能耗成本最小化，基于目标可以得出用户的用电最佳调度计划。

1)由式(4)得：

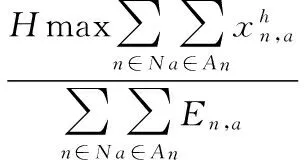
(9)

因此，最优化问题即为解决下式最小化问题：

(10)

如果假设总能耗固定，那么问题进一步转化为：

(11)

2)用户能源消费最小化，即：

(12)

用bn表示用户所要支付的费用，其取决于用户每天的用电量以及电价函数，假定用户n的支付费用为：

(13)

其中ph为电价函数，形式为：

(14)

其中ah，bh，ch为常数且不小于0。

在某时段h，用户的费用与他们的用电量是成正比的，则进一步假定：

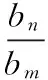
(15)

由上式可以得到用户n的费用的计算式如下：

(16)

由(17)可知，每个用户的费用不仅与自身的用电量有关，还与其他用户的用电量有关，用户n的效用函数为Pn(Xn；X-n)。

(17)

通过选取最优的脉冲信号占空比,可利用电压变换电路实现将在一定范围变化的电压转换为稳定的12 V电压源。对不同输入电压情况下,选取的最优化脉冲信号占空比进行分析,得到脉冲占空比随输入电压变化关系,拟合曲线后如图8所示。图中D为脉冲信号占空比,U为整流电路输入端输入的交流电压,可以看出最优占空比随输入电压成指数递减。根据拟合曲线可以得到占空比与输入电压的关系,从而在控制电压变换电路时参考该曲线就能得到理想的占空比数据,当电路检测到输入电压,根据曲线设置脉冲占空比,输出电压即为12 V。

3 实验仿真

假定有10个用户参与智能控制系统模型仿真，每个用户的家用电器分为不可调度负荷电器和可调度负荷电器两类，如表1和表2所示。

表1 不可调度设备负荷

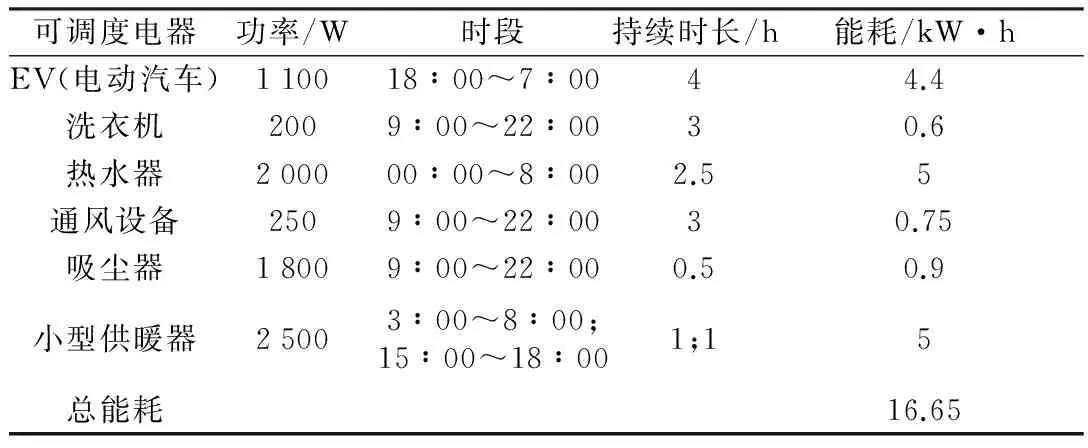
表2 可调度设备负荷

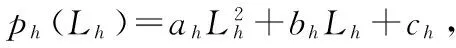
将式(18)效用函数改写如下:

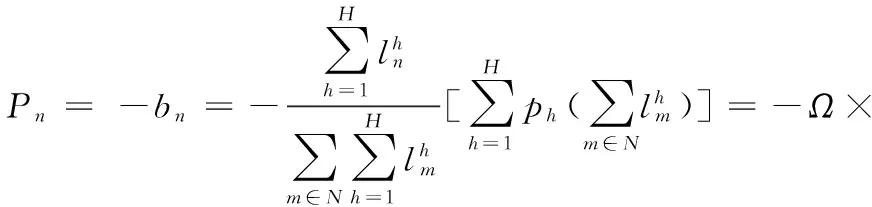
(18)

在本文模型中，各用户均不改变自己的总用电量，式中Ω为常数，问题转变为：

(19)

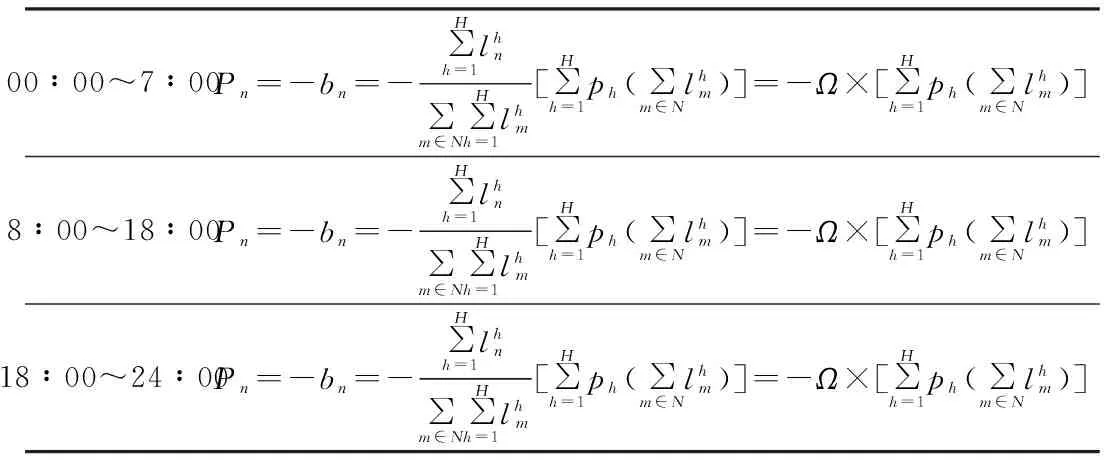
表3 分时电价

使用MATLAB中的fmincon函数，求解此类多元非线性规划问题。求解过程如下：

(1)初始化10个用户分时总负荷；

(3)将用户1新的用电规划与其余9个用户的分时负荷叠加，形成新的总负荷；

(4)在此负荷下用户2放弃原用电计划，重新规划自己的分时负荷，以满足式(20)；

(5)将用户2新的用电规划与其余9个用户的分时负荷叠加，形成新的总负荷；

(6)更多用户分别重新规划自己的分时负荷，直到单用户能耗花费稳定在均衡值。

图4 规划前单用户负荷

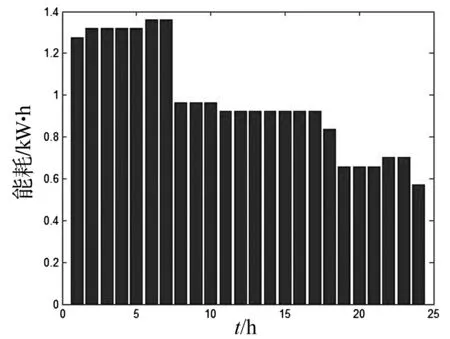
图5 规划后单用户负荷

在使用智能控制系统之前，如图4所示住宅用户的能耗峰值集中在20点以后，也就是高电费时段，使得21点的总负荷达到峰值15.91 kW，峰均比PAR=1.73，并且负荷曲线与分时价格正相关，所有用户总能耗支出为每天103.27元。

在使用智能终端后，随着更多用户分别规划自己的用电，总负荷峰值逐步转移至凌晨低电价时段，峰谷逐渐颠倒，又因为效用函数为分时总负荷的二次凹函数，不会导致负荷过度集中在低价时段，图5为第10位用户规划用电后的总负

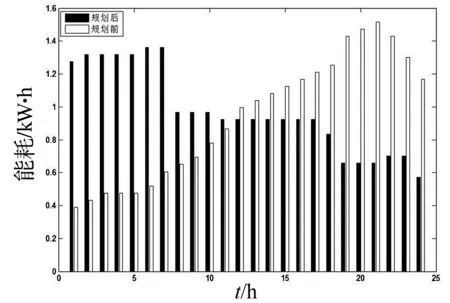
图6 规划前后单用户负荷

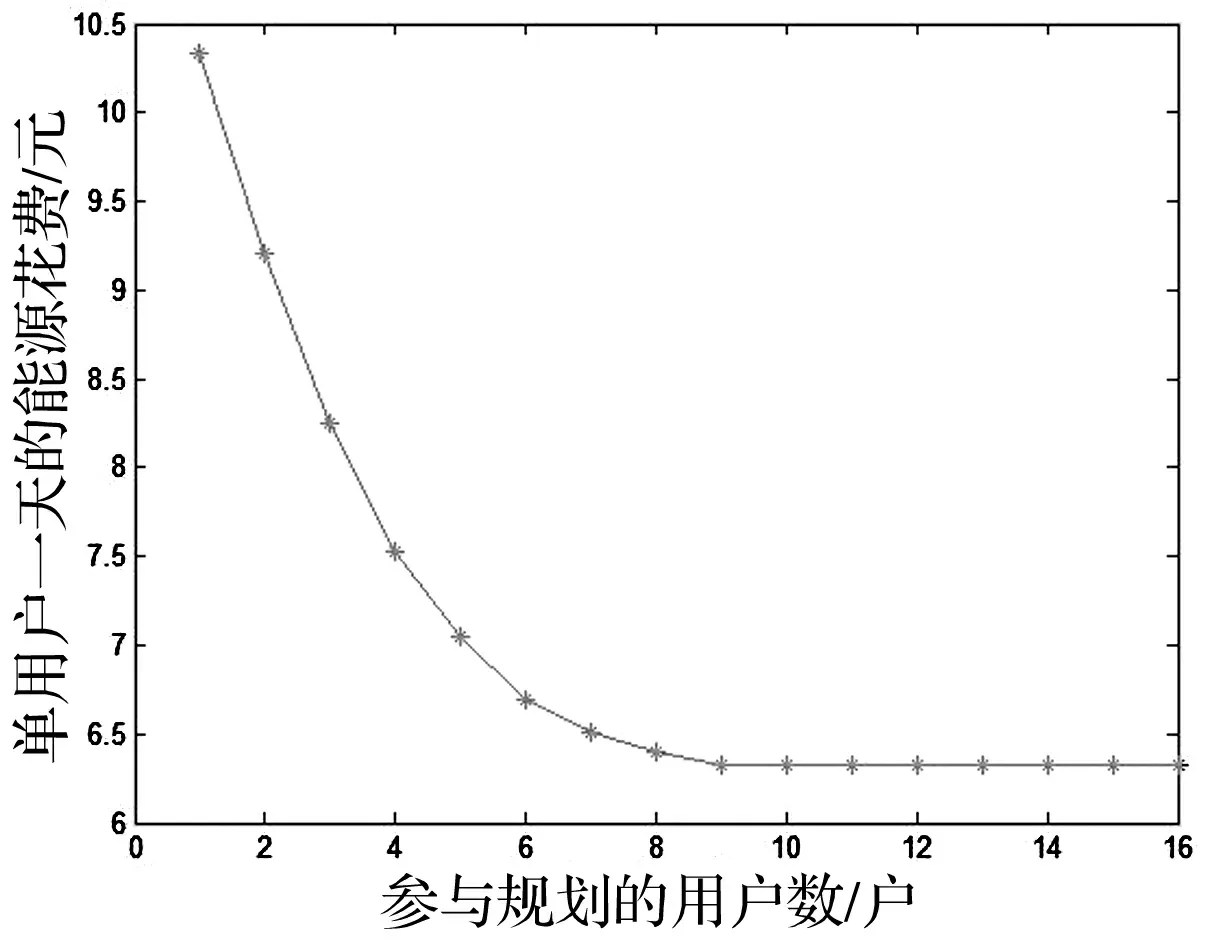
图7 用户平均电费与参与规划用户次数

荷图，峰值出现在7点，为13.61 kW，峰均比降低为1.48。在第10位用户规划完自己的用电计划后，所有用户能耗花费之和达到均衡值，为63.33元。规划前后分时能耗对比如图6所示。

从图7可以看出，每增加一个参与规划的用户，平均能源花费就会降低，直到达到最低值6.33元，所用用户的效用达到最大。规划前后能耗消费对比可得出所有用户能源花费从103.27元降至63.33元，这样一天下来所有用户共节省花费39.94元，长远看来经济效益可观。

4 结束语

本文提出的智能终端设备具备的电力计量和电力设备分时消费功能，实验结果表明，该智能终端所具备的博弈论算法可以大大降低用户消费，改善电力系统负荷峰均比。在本文仿真中，为方便讨论，对终端用户的设计比较简单，在实际生活中，不同用户的用电情况会更加复杂，并且本文中的电价模型设计比较简单，以后的研究中会讨论这些设置的合理性。

[1] 卢强,陈来军,梅生伟.博弈论在电力系统中典型应用及若干展望[J].中国电机工程学报,2014,34(29):5009-5017.

[2] 杨文轩,何光宇,王伟,等.用户侧能量管理原型系统的设计与实现[J].电力系统自动化,2012,36(20):74-79.

[3] 张伯泉,张旭红,贾茂盈,等.基于状态记忆的智能插座研究[J].测控技术,2014,35(33):125-131.

[4] 董思乔,赵荣建,孙通.基于WiFi构建的智能家居控制系统的设计[J].电视技术,2015,39(4):89-91.

[5] 陈星莺,陈璐,廖迎晨,等.考虑可中断负荷和需求侧竞价的供电电价模型研究[J].电力需求侧管理,2010,12(5):114-118.

A Research on the Smart DSM Control System Based on Price Game

Qin Chao, Liu Chuanqing, Chen Long, Pei Qian, Lu Shuang

(College of Electrical Engineering, Nanjing Institute of Technology,Nanjing Jiangsu 210044, China)

10.3969/j.issn.1000-3886.2017.03.008

TM744

A

1000-3886(2017)03-0023-03

定稿日期: 2016-10-29

本文得到南京工程学院创新基金资助(CKJB201309)

秦超(1989-)，男，江苏徐州人，硕士生，主要研究方向：电力经济，需求侧管理。 刘传清(1964-)，男，湖北鄂州人，博士，教授，主要研究方向：智能电网、电力通信。 陈龙(1990-)，男，江苏宿迁人，硕士生，主要研究方向：电力系统中博弈论优化。 裴谦(1990-)，男，江苏宿迁人，硕士生，主要研究方向：配电网智能技术与协同装备。 卢双(1993-)，男，江苏徐州人，硕士生，主要研究方向：新能源发电。