预测电流控制双开关型双Buck并网逆变器
卢德祥,王武,蔡逢煌
(福州大学 电气工程与自动化学院,福建 福州 350116)
预测电流控制双开关型双Buck并网逆变器
卢德祥,王武,蔡逢煌
(福州大学 电气工程与自动化学院,福建 福州 350116)
双Buck逆变器具有可靠性和效率高的优点,常被用作新能源发电和不间断电源的解决方案。双Buck逆变器存在输入电压高、双极性调制的缺点,采用双开关型双Buck逆变器消除这些不足,双开关型双Buck逆变器主要采用滞环电流变频控制,谐波频谱宽、滤波器设计困难,对功率器件的开关速度要求高;为此,采用SPWM控制方式实现逆变并网,使谐波频谱固定易滤除;同时通过预测电流控制策略消除电网电压扰动,提高逆变器的性能。最后通过PSIM仿真验证了理论分析与设计的可行性。
预测电流控制;双Buck逆变器;并网逆变器;仿真;可靠性
Abstract: Dual-buck inverter, characterized by its high reliability and efficiency, is used as solution of new energy generation and uninterrupted power supply. The dual-buck inverter’s disadvantages of high input voltage and bipolar modulation can be eliminated through adoption of the two-switch dual-buck inverter with hysteresis current frequency control and wide harmonic spectrum, which leads to difficult filter design and requires high switching speed of power devices. In this background, SPWM control mode is adopted to realize inverter grid connection and make it easy to filter out harmonic spectrum fixation. In the meantime, a predictive current control strategy is adopted to eliminate grid voltage disturbance and improve converter performance. Finally, PSIM simulation verifies the feasibility of the theoretical analysis and design.
Keywords: predictive current control; dual-Buck inverter; grid-connected inverter; simulation; reliability
0 引 言
航空航天、不间断电源和军民两用逆变器对可靠性及效率要求高,双Buck型逆变器具有无桥臂直通隐患、无体二极管反向恢复问题,是此类变流器运用的解决方案之一[1]。双Buck逆变电路在提高效率和可靠性的同时,也引入了新的问题[2]:(1)输入电压通常为全桥逆变器的两倍,器件电压应力大,为获得交流220 V输出,直流母线电压需大于700 V;(2)输入需分压大电容,存在母线不均压问题,在控制策略上需进行母线均压调节;(3)桥臂输出电压为两态电平,双极性调制谐波含量大,增加输出滤波器体积与重量。为解决这些不足,文献[3]提出双开关型双Buck逆变电路。该电路为全桥结构,输入无需分压大电容,直流母线电压利用高,器件电压应力小一半;桥臂输出为三态电平变化,谐波含量低。文献[3]针对双开关型双Buck提出采用模拟电路搭建的滞环电流控制方式实现,滞环控制为非线性控制技术,具有快速动态响应、电流易跟踪和内在限流的特点,在双Buck型逆变器中得到广泛运用。然而,滞环脉冲电流和开关噪声,导致谐波频谱宽,输出滤波器设计困难[4];采用变滞环宽度的滞环电流控制实现开关频率的恒定,可降低谐波含量,但这种控制方式增加了控制电路的复杂性;逆变器并网时忽略了电网电压扰动带来的影响,恶化了控制效果[5]。此外,在功率较大的运用场合,通常采用IGBT作为开关器件,为防止过高的开关频率损坏IGBT,需增加额外的限频电路。
为解决以上不足,提出基于预测电流法SPWM控制的双开关型双Buck并网逆变器。预测电流控制抑制电网电压扰动对并网电流的影响;恒定开关频率的SPWM控制谐波频谱固定易于分析,简化输出滤波器设计;不需增加限频电路,节约成本、保护了IGBT等开关器件的可靠工作。最后,通过PSIM与Visual studio软件联合搭建一个输出功率1 kW的双开关型双Buck并网逆变器仿真电路,验证了理论分析和设计方法的可行性。
1 SPWM调制双开关型双Buck并网逆变器工作原理
预测电流控制双开关型双Buck并网逆变器如图1所示,其中L1和L2为逆变器输出滤波电感值为L,对应的电感电流分别为iL1和iL2,Vd为输入直流电压,vg、ig分别为电网电压和入网电流,vgf和iLf分别为进入控制器的电网反馈电压和并网反馈电流,参考电流为iref。与传统双Buck电路相比,增加了开关管S3和S4,二极管D3和D4,等效组成两支单向开关,因此被称为双开关型双Buck逆变器。
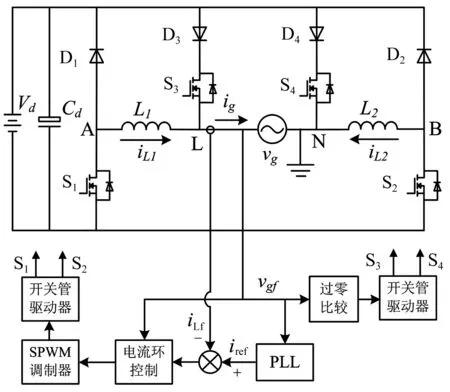
图1 双开关型双Buck并网逆变器
如图2所示为双开关型双Buck并网逆变器稳态时在一个工频周期的4个工作模态,图3所示为所对应稳态时的关键点波形,其中Vds1和Vds2分别为开关管S1和S2漏源极两端电压波形。在工频正半周时对应的工作模态为模态1和模态2,由图2和图3可知,此时ig>0,开关管S1、S4关断,S3常闭和D3构成一个正向导通的开关,S2高频工作、二极管D2完成续流,构成正半周Buck电路工作模式。

图2 SPWM控制双管双Buck工作模态
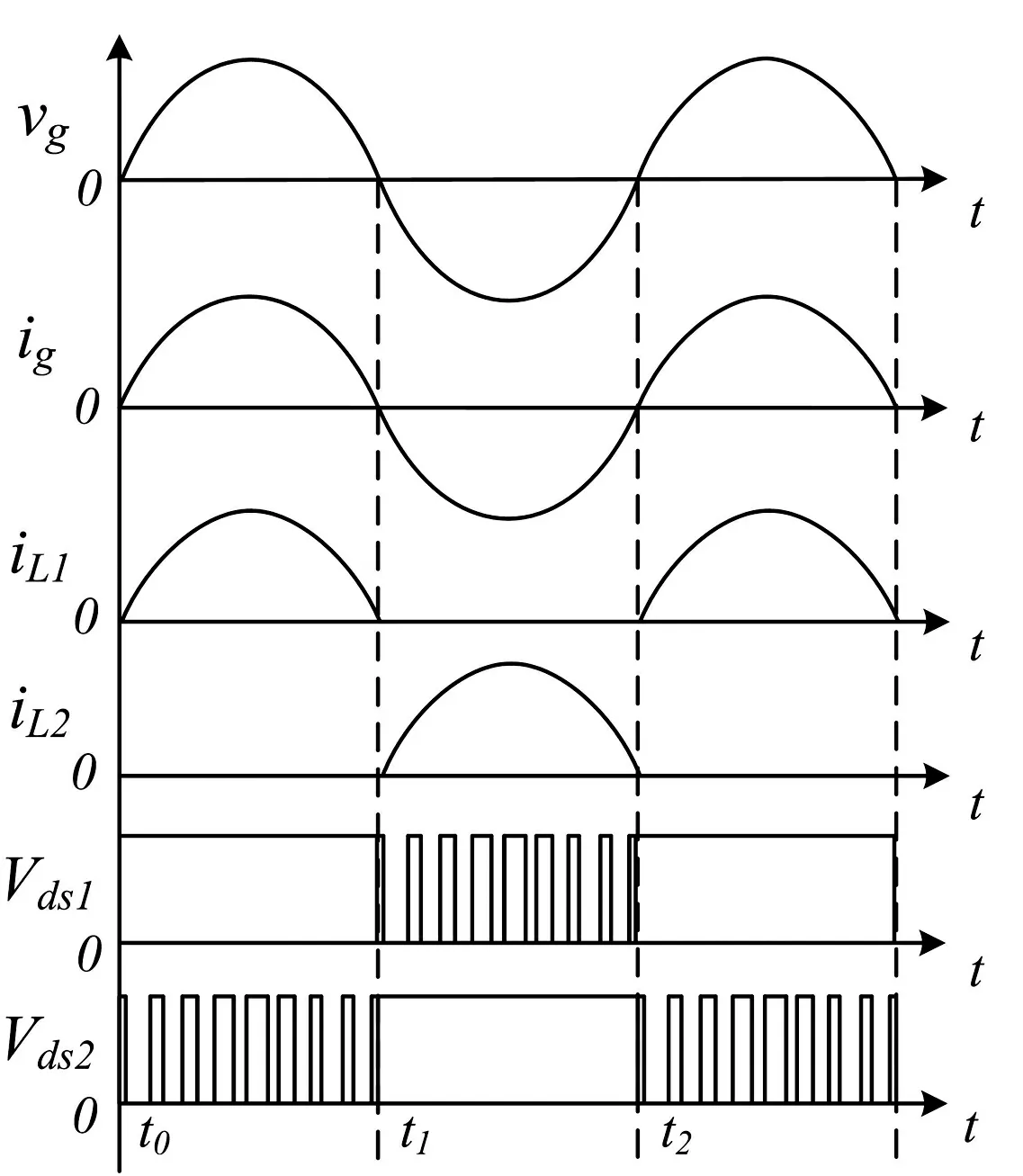
图3 SPWM控制双管双Buck关键波形
工作模态1:电路工作在Buck储能模式,S2导通,D2承受反压截止,输入电压Vd与电网vg的差值施加在电感L2上,电感电流iL2线性上升,电感电流iL2变化率为:
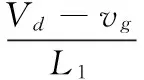
(1)
工作模态2:电路工作在Buck续流模式,S2断开,D2承受正向电压导通,电网电压vg反向施加在电感L2,电感电流iL2线性下降,电感电流iL2变化率为:

(2)
由式(1)和(2)可得输入和输出电压关系式为:
vg=d2Vd
(3)
其中d2为开关管S2的占空比。
在工频负半周时对应的工作模态为模态3和模态4,由图3和图4可知,此时ig<0,开关管S2、S3关断,S4常闭和D4构成一个正向导通的开关,S1高频工作、二极管D1完成续流,构成负半周Buck电路工作模式。负半周为正半周对称工作,同理分析可得输出电压与输入电压关系式为:
vg=-d1Vd
(4)
其中d1为开关管S1的占空比。
2 预测电流控制分析
双开关型双Buck逆变器工作时正负半周对称,因此以正半周工作为例进行分析。采用L型滤波器的并网逆变器电感电流即入网电流,正半周工作时,由基尔霍夫定律和拉氏变换可得电感电流iL(s)为:
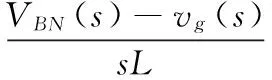
(5)
并网时最直接的瞬时控制电感电流的方式为采用比例调节跟踪电网电压正弦波形,将图1电流控制环中用比例调节器替换可得,其占空比d(s)在复频域上的表达式为:
d(s)=kp(iref(s)-iLf(s))
(6)
其中kp为比例系数,iLf(s)为电感电流测量值,iref(s)为电流给定,由式(3)、(5)、(6)结合开关周期为Ts的零阶保持器做Z变换可得电感电流iLf(z)的表达式为:

(7)
由式(7)可知对应的控制框图如图4(a)所示,当kp取得无限大时才可消除电网电压对电流环的扰动,这在实际运用中是不可取的。逆变器并网时仅采用比例P调节控制,并网电流受到电网电压扰动的影响使得被控电流无法线性跟踪给定电流,若采用PI控制则需调节比例系数和积分系数,增加调试难度。为此,提出如图4(b)所示离散化的预测电流控制框图,单L滤波器的并网逆变器等效成物理环节,软件实现的控制部分等效为软件环节。获得图4(b)预测电流控制方法的分析过程如下:

图4 电流环控制框图
假设电路工作在[k,k+1]开关周期内做线性化处理,桥臂点B与零线N的电压变化值表示为:
(8)
并网时控制目标为电感电流在[k+1]处的值即采样值iLf[k+1]跟踪参考电流的值iref[k+1]的值,并由式(8)可得软件环节控制器的输出占空比表达式为:
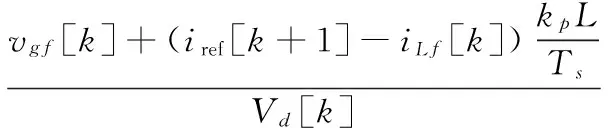
(9)
由式(9)和逆变器物理环节相结合可得图4(b)所示的预测电流控制双开关型双Buck并网逆变器的控制框图,且电流环的输入到输出传递函数为:
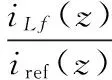
(10)
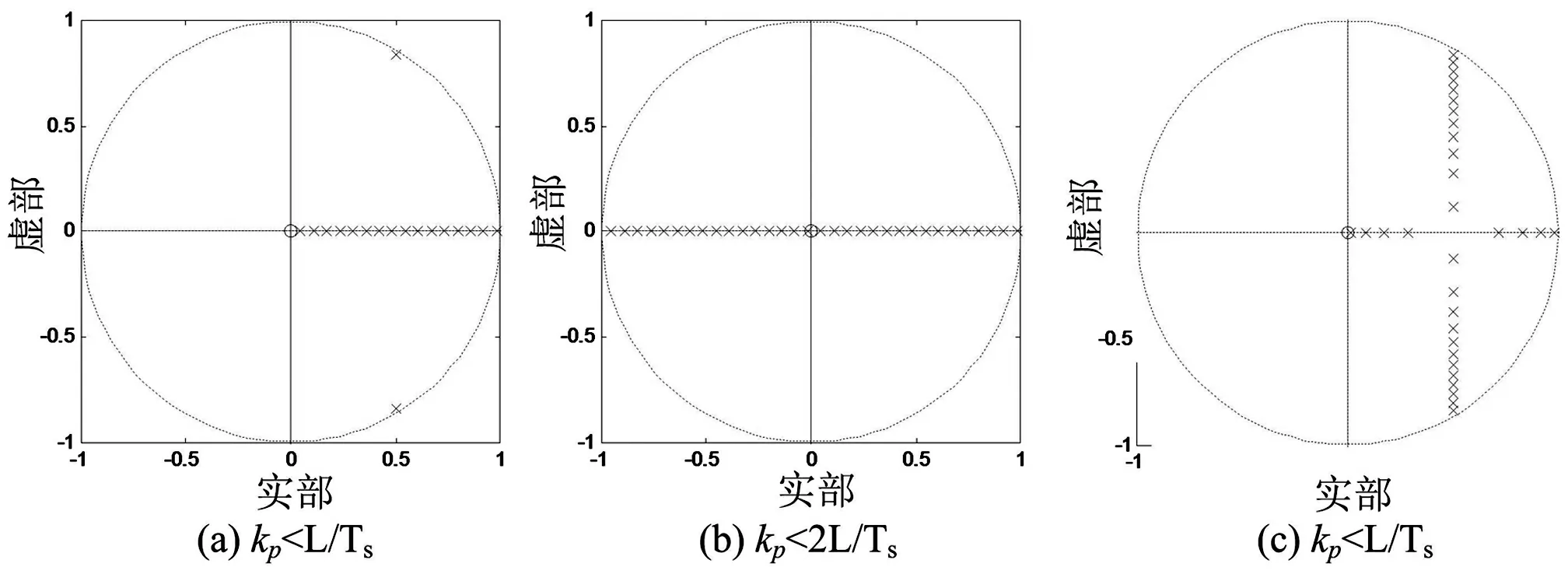
与式(7)相比,采用预测电流控制后,电感电流iLf(z)的表达式已不含电网电压扰动项。不考虑系统时延的前提下,取仿真电路参数,开关周期Ts=25 μs、电感L=1.6 mH,图5(a)和(b)给出了式(10)的零极点随比例系数kp的变化图,离散系统稳定的冲要条件是系统的极点分布在单位圆内,图5(a)中比例系数kp小于电感L与开关周期Ts的比值时极点落在实轴的右半部分系统为低通输出,当L/Ts 仿真采用数字控制形式实现逆变器的逆变并网,存在考虑系统控制时延,图4(b)占空比d[k]输出前需增加一个零阶保持器Z1,式(10)在增加零阶保持器后变为: (11) 图5 电流环传递函数零极点随kp变化分布图 式(11)的零极点随比例系数kp变化的分布如图5(c)所示,当kp>L/Ts时系统将不能够稳定,为了保持控制系统的稳定和低通特性比例系数需满足kp 为了验证以上理论分析,用PSIM搭建仿真电路与Visual studio C++编写控制程序、运用同步锁相技术[6]实现双开关型双Buck逆变器的并网仿真,逆变器并网采用单L滤波器,仿真参数为:输入母线电压360 V,电网电压220 V/50 Hz,开关频率40 kHz,输出功率1 kW,两支滤波电感为2 mH。 图6(a)为采用电流环比例控制给定为满载输出时的仿真结果,并网时采用比例控制无法跟踪电流给定;图6(b)(c)为采用本文提出的预测电流控制方式的仿真结果,(b)为给定半载时的输出波形、(c)为给定满载时的并网波形,满载时仿真并网电流THD=6.4% 、PF=0.997,可知双开关型双Buck并网逆变器在采用提出的预测电流控制策略可准确实现电流跟踪给定;图6(d)为开关管S1、S2和并网仿真波形,采用半周期SPWM调制方式可实现开关频率的恒定,有利于并网滤波器的设计。 图6 双开关型双Buck并网逆变仿真波形 针对逆变器可靠性要求高的运用场合,给出了一种预测电流控制的双开关型双Buck并网逆变设计方案。通过预测电流恒频控制方法,解决了采用滞环电流控制的双开关型双Buck逆变器存输出谐波频谱宽,控制环受电网电压扰动影响、跟踪不准确的不足。所提出的控制方法仅需进行比例参数调试,缩短了调试周期,便于工程运用。仿真结果验证了预测电流控制的SPWM调制双开关型双Buck逆变器可良好实现逆变并网。 [1] HONG F, LIU J, JI B, et al. Single inductor dual buck full-bridge inverter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8):1-1. [2] 洪峰, 单任仲, 王慧贞,等. 三电平双降压式全桥逆变器[J]. 中国电机工程学报, 2008, 28(12):55-59. [3] YAO Z, XIAO L. Two-switch dual-buck grid-connected inverter with hysteresis current control[J]. IEEE Transactions on Power Electronics, 2012, 27(7):3310-3318. [4] HONG F, LIU J, JI B, et al. Interleaved dual buck full-bridge three-level inverter[J]. IEEE Transactions on Power Electronics, 2015, 31(2):1-1. [5] 蔡逢煌, 江彦伟, 王武. 基于解耦控制的单相并网逆变控制算法[J]. 电气自动化, 2015,35(5):40-42. [6] 蔡逢煌, 郑必伟, 王武. 结合同步锁相的光伏并网发电系统孤岛检测技术[J]. 电工技术学报,2012,27(10):202-206. Two-switch Dual Buck Grid-connected Inverter with Predictive Current Control Lu Dexiang, Wang Wu, Cai Fenghuang (College of Electrical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350116, China) 10.3969/j.issn.1000-3886.2017.03.001 TM464 A 1000-3886(2017)03-0001-03 定稿日期: 2016-10-11 卢德祥(1990-),男,福建龙岩人,硕士,研究方向:电力电子装置及其控制技术。 王武(1973-),男,福建莆田人,博士,教授,研究方向:滤波技术、电力电子系统建模与控制研究。 蔡逢煌(1976-),男,福建莆田人,博士,副教授,研究方向:新能源发电、电力电子系统建模与控制实现。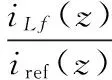
3 仿真分析

4 结束语

