高中生元认知能力对地理综合题解题水平的影响研究

摘要：地理综合题是检验学生地理问题解决能力的重要工具，在地理测试中占有重要地位。假设元认知能力是影响高中生地理综合题解题水平的因素之一，通过多次测试和修改完善开发出高信度和高效度的元认知能力测量量表，并通过测试获得了云南省下关第一中学49份有效样本的元认知能力和综合题解题水平数据，借助SPSS 19.0软件，运用相关分析、独立样本t检验、回归分析等方法，可证明元认知能力与综合题解题水平之间存在显著的相关性。

关键词：地理综合题；元认知能力；解题水平；启发式提问清单法

一、问题的提出

各地高考地理试卷的题型有选择题和综合题两大类，其中综合题的比重一般超过一半，而且高考综合题难度较大，如浙江省2010—2013年高考综合题的难度系数均小于0.5，是考生失分的“重灾区”。国内有一些关于地理综合题解题训练的研究，如许国鹏从应试角度归纳出审题、析题、答题的解题步骤，并展示解题策略的思维导图；汤国荣从命题角度分析地理综合题的价值取向、命题特点，提出针对性的复习策略。地理综合题灵活多变，对学生的地理知识和地理问题解决能力的考查十分全面，提高综合题的解题水平需要了解影响学生综合题解题水平的因素，并把握其中规律性的原理和机制，而在这方面，尚未发现有研究去探讨，更无实证研究的成果。本文认为，地理知识丰富程度、地理思维能力是影响地理综合题解题水平的最基本因素，而元认知能力也是一个重要的因素，本文将从实证的角度探讨元认知能力对地理综合题解题水平的影响，在地理知识和思维能力水平不能短期提高的情况下，为从元认知角度提高解题水平提供实证依据。

二、研究设计

要发现元认知能力对地理综合题解题水平的影响，首先要对学生的元认知能力和地理综合题解题水平进行测量，并通过多元化的样本将地理知识水平、地理思维能力水平设为控制变量。研究中元认知能力的测量最为关键，需要开发高质量的测量工具并测得可信的数据，是研究的难点；另外需要通过测量获取学生的地理综合题解题水平数据。之后借助SPSS软件，运用相关分析、回归分析、独立样本t检验、曲线拟合等方法揭示元认知能力和地理综合题解题水平之间的统计关系，并論证其因果关系，最终从提高元认知能力的角度提出提高地理综合题解题水平的教学策略。

三、元认知能力与地理综合题解题水平的测量

1.元认知能力测量量表的开发

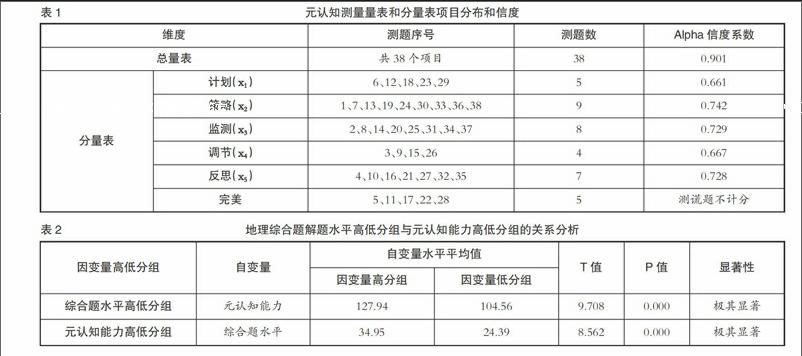
笔者重点选取元认知知识和元认知监控这两项容易量化的指标，并将其细分为计划（x1）、策略（x2）、监测（x3）、调节（x4）、反思（x5）五个维度进行地理综合题解题元认知能力测量量表开发。量表内容参考国内外相关元认知问卷中的题项，测题内容采用李克特五分量表法计分，量表全部为正向题，按照表述与其实际情况相符程度的五个等级（非常符合、符合、一般、不符合、非常不符合）分别计以5、4、3、2、1 分。试测均在云南省下关第一中学进行，研究结论暂时只对该校样本负责，是否为普遍规律有待更多研究案例的重复和验证。2016年3月16日在高三年级发放127份测量量表，有效回收113份；2016年4月6～11日，在高二、高三年级8个文科班发放450份测量量表，有效回收433份。对量表进行质量分析和完善的过程中，将量表测题由43题减少为38题，量表信度由0.897上升到0.901，5份分量表的信度也相应提高，信度在0.661～0.729之间（如表1），量表具有非常满意的信度。另外，皮尔逊相关分析数据还显示，大部分题项与所代表维度的综合分的相关性高于与其它维度的综合分的相关性（数据略），说明该问卷具有较好的结构效度。综上表明，量表质量较高，测试数据可以用于研究。量表中的5道完美性测试题作为测谎题，用于识别样本数据的真实性，不计分，33道计分题测得的元认知能力满分为165分，最低为33分。

2.地理综合题解题水平的测量

对综合题解题水平测量最权威的工具是文综地理试题，本研究选取2016年8月26日举行的新高三学生综合测试为依据。试卷中的第36、37题地理综合题，包括6道小题，总分值为46分。经地理教师论证这两道综合题非常经典，具有较高的测试信度和效度，并且融合自然地理、人文地理和区域地理的知识，对学生的地理学科能力、地理基本方法、地理基本观念进行综合考查，题目图文信息充分和适切，设问基本包括综合题的大部分类型，如原因类设问、评价类设问、比较类设问等。本次考试由学校组织，是非常正式考试，能够客观真实地反映学生的综合题解题水平，试卷评阅完成后，从教务处获得学生的每题得分数据，将综合题成绩提取，作为学生综合题解题水平的研究数据。所有文科学生总体的地理综合题平均分为30.12分，平均得分率为65.48%。

3.元认知能力测试与地理综合题解题水平测量数据的连接

2016年9月9日对高三（8）班（文科班）的50名同学进行元认知能力测试，最终获得有效数据样本49份，将这49份样本的元认知能力与其地理综合题解题水平数据进行连接，用于元认知能力和地理综合题解题水平的关系分析。49份样本的元认知能力平均分为118.93，标准差为10.84，其地理综合题的平均分为30.21，标准差为5.07。

四、高中生元认知能力与地理综合题解题水平的关系分析

1.元认知能力与地理综合题解题水平之间具有因果关系（如表2）

采用皮尔逊相关法研究元认知能力与地理综合题解题水平间的相关关系，两者的相关系数为0.718，相关系数值较高，显著性概率P值为0.000，相关关系极其显著，说明元认知能力与综合题解题水平之间具有显著的相关性。

为进一步验证元认知能力和综合题解题水平之间的关系，将样本按照地理综合题解题水平进行划分，把综合题解题水平前27%（13名）列为高分组，后27%（13名）列为低分组，通过独立样本t检验分析综合题解题水平高低分组学生的元认知能力的均值是否有显著差异；然后按同样方法将样本的元认知能力水平分为高分组和低分组，通过独立样本t检验分析元认知能力高低分组学生的地理综合题解题水平的均值是否有显著差异。两次均值比较的差异显著性水平P值均为0.000，说明差异极其显著的水平，显示两个因素之间均互为条件性因素。国内外的文献研究也都说明元认知能力与问题解决能力之间有因果关系，因此，统计数据证实了元认知能力与综合题解题水平之间因果关系的存在。据此可认为，提高元认知能力可以促进学生的地理综合题解题水平的提高，这也是本研究提出以启发式提问清单法（基于元认知能力的提高）来提高学生地理综合题解题水平的依据。endprint

2.元认知能力与地理综合题解题水平之间呈现复合函数关系

运用SPSS19.0软件，以学生的综合题解题水平作为因变量，元认知能力作为自变量进行回归分析，经曲线拟合发现用复合函数模型拟合最为理想（如图1），所得复合函数模型的回归方程为：Y=6.557×1.103x，其中Y为综合题解题水平，x为元认知能力。

回归方程的P值为0.000，小于0.01，说明元认知能力与地理综合题解题水平间的复合函数关系极其显著；R方为0.65（>0.6），说明曲线拟合优度较好，回归方程中元认知能力对地理综合题解题水平具有较强预测能力。

五、提高高中生地理综合题解题水平的教学策略

美国数学家和数学教育家G·波利亚在1945年提出了启发式自我提问法来解决问题。他将解决数学问题分为理解问题、制定计划、执行计划与回顾四个步骤[1]。在每个步骤下，都有相应的自我启发式问题或步骤，类似于元认知的出声报告法，将元认知的解题过程用语言表达出来，由此让学生理解和熟悉元认知的作用过程，从而自觉地在解题过程中运用。这个方法虽然属于数学问题解决的方法，但被公认可以适用于其它学科，因此同样也可以用于地理综合题的解题过程。如果能将解题中的元认知过程直观地展示于纸上，让学生思考并体悟，相信对学生元认知能力的提高将会大有帮助。笔者将这种方法称为启发式提问清单法。

1.地理综合题解题启发式提问清单的编制方法

根据相关文献，结合自己的思考和教学经验，笔者编制了地理综合题解题中的启发式提问清单。①理解问题。这个问题的行为动词是什么？指的是什么意思？读题后，你发现哪些知识与这个问题有联系？如果有图，图中有没有与这个问题相关的帮助信息？老师有没有讲过类似的题，当时是怎样分析的？②制定计划。解决这样的问题，一般要用哪一种模型？参照分值，估计这道题的答题要点有几点？是不是需要画出思维导图，以帮助分析和解答？如果还不清楚，是否要再读一遍文字材料和图片信息？③执行计划。在解题中，要提醒自己注意——在书写答案时，是否紧扣材料，利用材料中的内容，有针对性地回答问题？解题过程中，我已经写了哪些内容，有没有漏写什么？有否使用专业的地理术语来答题？答案有效吗？有逻辑性吗？能不能说明这个地理现象？我的答案是…… ④回顾。做完题目后，我会问自己：这道题用了哪个模型，知识点间是怎样联系起来的？对比参考答案和他人答案，我的有哪些不足和优点？解题中最大的失误是什么，以后要如何弥补？我的解题方法能用到哪些类型的问题上？我的总结是……

教师可根据遇到的问题对清单进行修改满足不同层次学生的学习需要。优等生清单中问题的数量可适当少一些，但要在关键性步骤上给予帮助，使其元认知能力更加完善。对学困生清单要尽可能详细，让学生掌握元认知能力在解题中运用的每一个步骤，逐步把外部的形式变成其内在的思维模式，从而提高元认知能力，进而提高地理综合题的解题水平。

2.地理综合题解题启发式提问清单法的应用

建議教师在训练学生的过程中让学生根据启发式提问清单进行回答。填完之后，教师也要展示自己的提问清单回答答案，供学生参考，师生互动，发现不足。同时，还应该准备一道类似的训练题，让学生脱离提问清单进行训练，起到迁移的作用。教师需要将提问清单的回答集中进行分析诊断，确定下一步教学计划。坚持训练将有助于学生的元认知能力提升，从而提高地理综合题解题水平，方法的具体效果有待进行实证研究。

启发式提问清单实际是将元认知过程中计划、策略、监测、调节、反思等环节展示于纸上的一种形式，它可以让学生直观地看到解决一道综合题的正确思维方式，并且通过不断的训练，把外部的要求内化为学生的思维方式，从而让学生养成运用元认知思考的习惯。同时也需要学生记住一些综合题解题模型，两者有机结合，学生的综合题解题水平就会显著地提高。启发式提问清单还能把原先模糊不清的元认知过程具体化，使元认知能力的提高变得具体可操作，教师能够清楚地看到学生的元认知过程，诊断其中的问题，使教学更有针对性。教师自己对提问清单进行回答并向学生展示，站在学生的角度思考问题，让学生明白解题中更合适的元认知过程，从而形成师生之间相互启发的教学生态。▲

参考文献：

[1] G·波利亚.怎样解题：数学思维的新方法[M].上海：上海教育科技出版社，2007.endprint