结合实例，浅谈利用“分析”解决实际问题

艾金巧

摘要：问题解决是集概念、逻辑思维、计算于一体的知识技能运用。通过培养学生将文字变成理清各种数学关系的图或文字——即：分析的能力，从而解决问题。

关键词：分析、运算关系、关键字（词）

【中图分类号】G623.5

每一个学科都有一个核心，小学数学学科的核心就是问题解决——解决生活中的数学问题。问题解决在课标中体现了它的重要地位，它是义务教育阶段数学课程标准的目标之一。它是集概念、逻辑思维、计算于一体的知识技能运用。然而许许多多的孩子，一遇到解决问题（应用题）就不知道该怎么办了，不知如何着手解决问题。时不时的可以看见他（她）们不停的抓耳挠腮或着一直盯着一道应用题目不转睛却毫无行为。如果学生们能够具备将若干文字变成简单的“分析”（理清各种数学关系的图或文字），那么解决问题就不再是学生们的困惑了。

在低段时期，首先要初步学会以数学的眼光，从生活中发现问题和提出问题，其次有目的的训练逻辑思维能力，能综合运用数学知识进行“分析”，最终解决生活中简单的实际问题。在一开始刚接触数时，培养学生说一句含有一个数的话，要联系生活，感受数在生活中的各个方面都存在，它可以表示不同的含义。比如：说一句含有数4的话。可能会说：我有4颗糖；草地上有4只兔子；一枝钢笔4元钱；现在是下午4点；我家在4单元等等，体会4可以表示数量、价钱、时间、地址等等。还可以任意给出3个相关联的数，让学生尝试编数学问题，以“说”促“思”，锻炼学生语言表达能力的同时，也训练孩子们的逻辑能力及发现运算关系的能力。例：5、8、13；根据这组数分别编出用加法运算和减法运算解决的数学问题。加法运算题：树上有5只猴，树下有8只猴，一共有几只猴？减法运算题：我有13元钱，花了5元，还剩几元？也可以给出具有乘除关系的3个数，让学生自主编题，有效锻炼逻辑思维能力。

伴随年级的增高，知识的积累，逻辑思维的提高，逐步培养通过“分析”解决问题的能力。让学生们经历克服困难、解决问题的过程，体验感受成功的快乐。

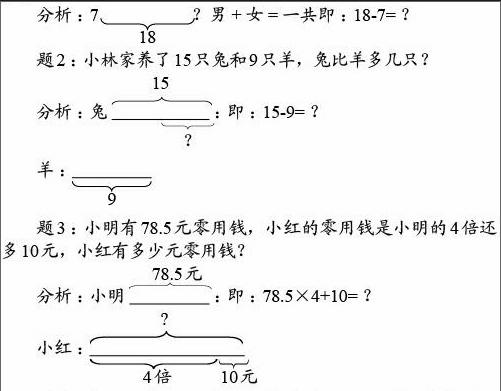
题1：我们班一共种了18棵树，男生种了7棵，女生种了多少棵？

到中、高段时期，可以把问题解决大致分为三类：关键词式、关系式式、公式式。拿到一道数学应用题，首先读一遍题后不但要能获得相应的数学信息，关键还要能够区分出它是哪一类应用题，再运用相应的“分析”进行问题解决。

关系式式问题解决分为：统一问题：每份数×份数=总数；行程问题：速度×时间=路程；价钱问题：单价×数量=总价；工作问题：工作效率×工作时间=工作总量等等。

第二问：（100-45.6）÷13.6

关键词式问题解决有：*是*的几倍；*比*的几倍多（少）几；*是*的几分之几；*比*多（少）几分之几；*是*的百分之几；*比*多（少）百分之几等等。有关“1”问题解决遵循一种办法：已知“1”用乘，求“1”用除。那么我们就要先根据关键词分析出题目是属于已知“1”的题还是求“1”的题，再用相应的运算解决问题。举例如下：

题1：甲是60，乙是甲的1/5，乙是多少？

分析：乙是甲的1/5，甲是“1”，问乙就是已知“1”，用乘，

即：60×1/5=乙。

题2：甲是60，甲是乙的1/5，乙是多少？

分析：甲是乙的1/5，乙是“1”，问乙就是求“1”，用除，

即：60÷1/5=乙。

题3：甲是60，乙比甲多3/5，乙是多少？

分析：比甲多3/5，就是比“1”多3/5，即：1+3/5，求乙是多少，“1”是甲，已知甲的具体量，因此用乘。

即：60×（1+3/5）=乙。

题4：甲是60，甲比乙多3/5，乙是多少？

分析：比乙多3/5，就是比“1”多3/5，即：1+3/5，求乙是多少，已知甲的具体量，求乙就是求“1”因此用除，

即：60÷（1+3/5）=乙。

题5：甲是20，比乙的2倍少4，乙是多少？

分析：这类题型也可用方程解决，便于找等量关系，能更好地理解和解决问题。比和少是关键词，比谁就设谁为X，少即是减，则比乙的2倍少4，就可以用2X-4表示。因为甲是20，所以：2X-4=20

这里的“甲、乙”可以具备丰富的含义，可以是车的速度，可以是物品的价钱，可以是每小时的工作量等等，具备现实含义，就使每道题充实了起来，变成解决贴合现实的生活中的数学问题。

公式式问题解决就需要学生在熟记每一道公式的同时理解每道公式的由来。主要就是解决图形相关的数学实际问题。利用关键词（透露出特殊关系的字词）和公式可以更加快捷、方便、准确地经历推导，分析出解决问题的有效方法。在解决问题时，将与已知条件（关键词）和问题有关的公式列出来，再将已知的量标记上，就可以找到解决问题的方法了。

例：已知一个正方体的水池表面积是125平方米，求占地面积是多少平方米？求它能容纳多少立方米的水？

分析：首先有关键词：正方体水池，即说明底面是正方形并且少一个面。其次提到表面积，则思考正方体的表面积公式。

在数学广角中的植树问题和鸡兔同笼问题一样可以运用“分析”解决问题。

在学习植树问题时，我们要学会将知识迁移。解决这部分问题的关键是能否弄清楚间隔数与棵数之间的关系。我们可将两头种树、一头种树、两头都不种树，抽象为学习过的线段、射线、直线。目的是能够更好地理解不同情况下棵数与间隔数之间的关系，以便于更好地解决植树问题。端點相当于棵数，线相当于间隔。线段的两个端点就好比两头种树的情况，之间有一个间隔，即棵数=间隔数+1。射线有一个端点就好比一头种树的情况，之间有一个间隔，即棵数=间隔数。直线没有端点就好比两头都不种树，只有一个间隔，即棵数=间隔数—1。

综上所述，也就是当学生们拿到印满密密麻麻的文字应用题时，端正心态，不嫌麻烦，边读题边将这些文字变成简单、直接的“分析”时，解决问题的方法就一目了然了。实则经历“分析”——理清思路的过程，最终使问题解决。endprint