WOA算法的非均匀稀布阵列优化方法
袁鹏亮,史 朝
(1.庆阳职业技术学院 能源工程系,甘肃 庆阳745000; 2.西北工业大学 电子信息学院,陕西 西安 710129; 3.成都信息工程大学 电子工程学院,四川 成都 610103)
WOA算法的非均匀稀布阵列优化方法
袁鹏亮1,2,史 朝3
(1.庆阳职业技术学院 能源工程系,甘肃 庆阳745000; 2.西北工业大学 电子信息学院,陕西 西安 710129; 3.成都信息工程大学 电子工程学院,四川 成都 610103)
鲸算法(Whale Optimization Algorithm,WOA)是最近新提出的一种仿生算法,具有操作简便、搜索快速的突出特点,有非常优异的应用前景。在阵列综合方面,WOA算法还没有引起重视,目前所知,还没有具体的应用文献记录发表。就WOA在阵列综合的非均匀线阵综合方法进行了有益的探索,通过对算法的适当改进和拓展,将WOA应用到非均匀阵列的约束性问题的优化上,主要实现了对非均匀阵列的阵元间距和数目约束的二元约束问题与主波束宽度的约束问题的优化。仿真结果表明,WOA算法对于非均匀稀布阵列的约束性优化问题是有效的,并且与GA和PSO算法等进化算法相比,WOA算法在计算速度和稳健性上有更大的优势。
鲸算法;阵列综合;非均匀线阵;稀布化
0 引言
阵列综合是电磁场与电磁波理论研究的一个重要方向,多年以来,已经广泛应用到雷达、微波和远程感知等诸多领域。在实际的工程应用当中,许多场合基于通信质量以及功率等诸多方面的考量,往往对于阵列天线的远场辐射方向图会提出一些特殊的要求,例如,在雷达扫描中,更多时候需要的是扇形波面,而在卫星通信领域,为了提高功率的节约和传输的准确性,需要的辐射方向图一般应该具有窄主瓣低旁瓣的特征,在地面的移动通信当中,则更多需要天线的远场方向图具有深零陷的特征,以便能够更好地解决信道的拥塞、对消干扰等现实问题[1]。
迄今为止,伴随各种通信技术的蓬勃发展和在生产生活的大量应用,广泛的需求使得阵列天线的远场辐射方向图的旁瓣压制成为阵列综合的重要的研究方向之一。通过旁瓣的压制手段使得旁瓣电平的峰值PSLL(Peak Sidelobe Level)减小,达到在某些干扰存在的扫描角度的干扰对消进而实现信道有效传输并且提高通信质量等目的[2]。
在最初,阵列综合的研究主要集中在均匀阵列上。而在文献[3],kumar利用分数阶勒让德变换法综合了非均匀线阵,取得了较低的PSLL效果。由于采用的方法并非迭代搜索型方法,在计算时间和内存节约上有了改善,尤其对于实际工程应用中的约束性问题适用,但文中没有涉及到孔径约束的问题研究。针对这一问题,在文献[4]利用改进的GA算法进行了具体的研究,尤其是在孔径约束和阵元个数约束的双重条件的规范下,取得了较文献[3]更好的结果,此后,在文献[5]针对这一算法在阵列稀疏化方面进行了进一步的研究。类似的研究还出现在文献[6-7]。随新算法的不断出现,对于一些类似GA的其他进化算法在阵列综合中的应用研究开始出现[8-13]。文献[14-17]就是利用PSO算法对文献[4]中算例的优化,结果表明可以优化出更低PSLL所需要的阵元间距分布。值得一提的是,基于压缩感知理论的阵列综合方法在文献[18-20]相继研究,这种方法将阵列综合理解为一概率性问题,利用快速相关向量机(RVM)来求解。目前数据表明,在计算效率上明显改善。另外,凸优化方法也被引入到阵列的综合当中[21-24]。
虽然以前的文献中已经提出了阵列综合的一些方法,但是对于时间和效率以及内存的节省等方面的综合考量,使得寻求一些新的算法显得甚为必要。WOA算法是2016年新提出的一种算法[25],计算快速便捷,目前所知还没有该算法在阵列天线研究领域的文献讨论过,本文就WOA算法在含有约束性条件的非均匀稀布阵列综合方面进行较为深入的研究。
1 阵列稀布化的模型建立
本文研究的阵列孔径假设限定在2L范围,若为奇数阵,则阵元的总数目可以写为2N+1,阵元呈中心对称分布且各向同性,阵元的激励为均匀等幅激励。当阵列孔径尺寸的约束条件存在,为了维持孔径长度,不妨可以取左右2个末端的阵元间距为dN=L,d-N=-L,进而通过算法来优化获取本算法最优的阵元位置。对于一个线阵,其远场辐射方向图可以表示为:

(1)
式中,In为第n个阵元产生的激励,在本文设定为1,不会对结果产生影响;θ为观察角,θ∈[0,180],u=cosθ;k为波数,k=2πλ。由于阵元的分布是中心对称,于是式(1)可以改写为:

(2)
对于正半轴,de若为最小的孔径约束长度,在半孔径L上剩余的可用于优化的有效孔径空间为:
SP=L-(N-1)de。
(3)
若把正半轴每个阵元的坐标表示为:
d=[0,d1,d2,…,dN-2,L],
(4)
那么,右半孔径的阵元位置矢量就为:
(5)
目的就是优化阵元位置矢量X,以得到PSLL较低的阵元位置矢量的分布。于是,针对X的约束条件可以描述为:
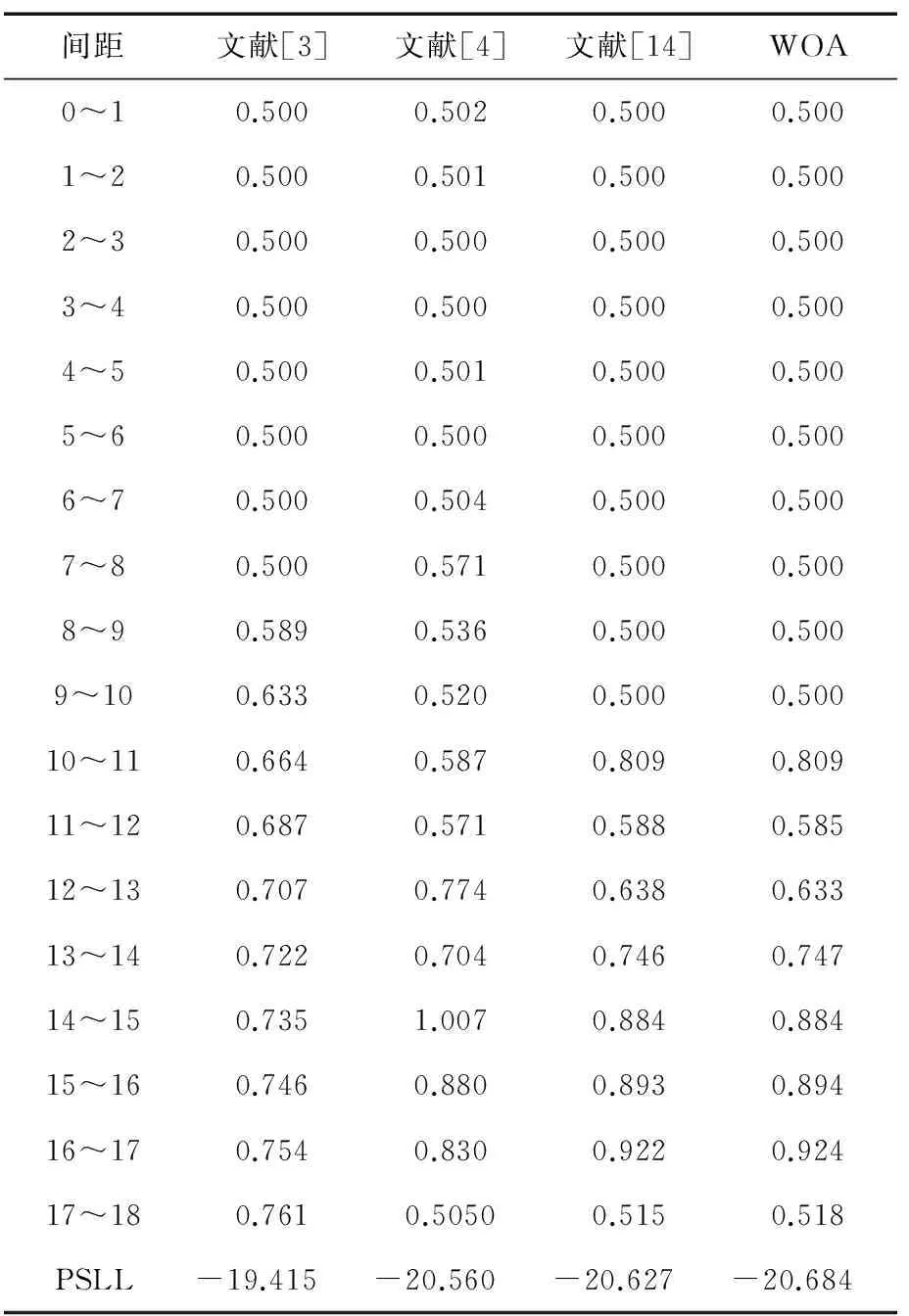
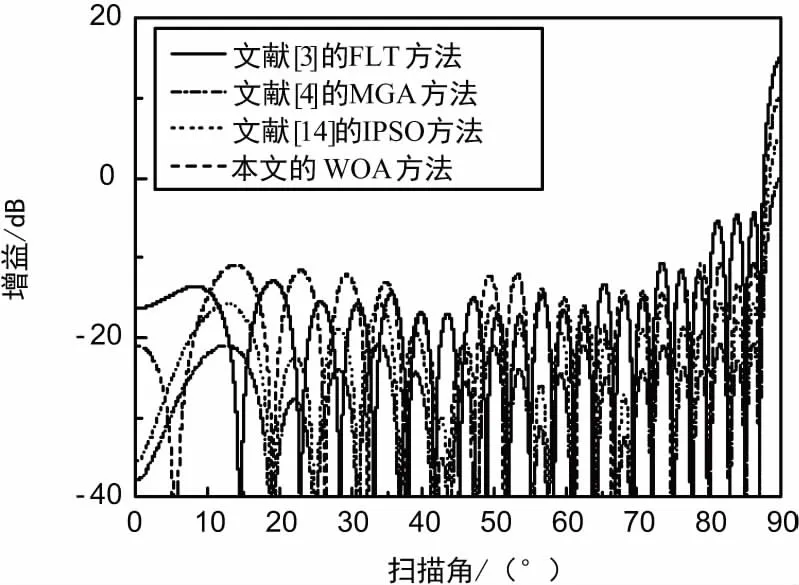
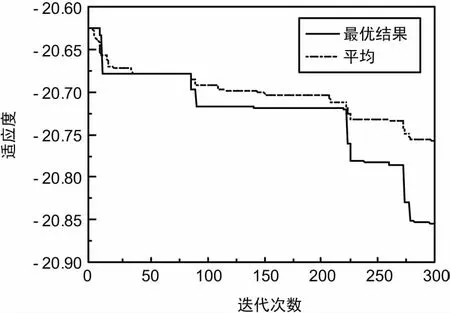
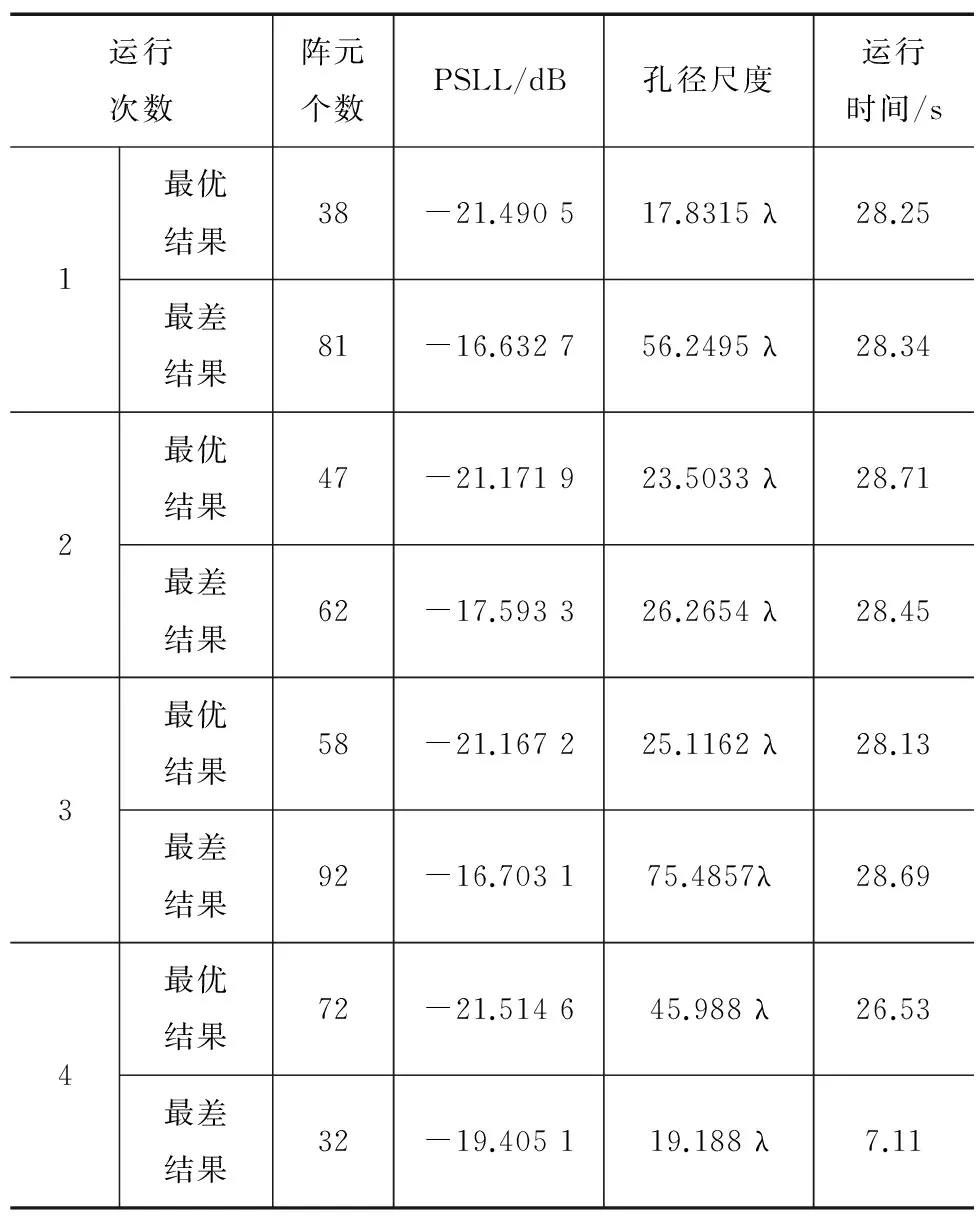
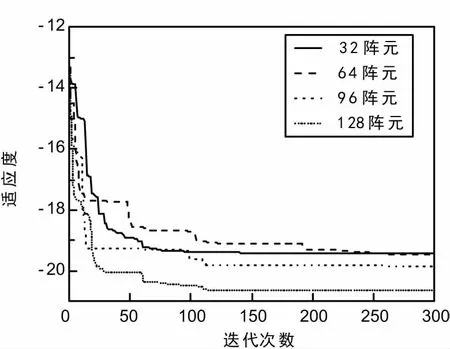
find{X|x1,x2,…,xN-2} (6) 式中,‖·‖为向量无穷范数;ΘM和ΘS分别为主波束、旁瓣波束的矢量空间。据此,算法的适应度函数可构建为如下形式: (7) 式中,Fmax为辐射方向图的最大幅值。在此,按照最小化的目标方向构造目标函数,目标函数则表示为: f(di)=min{fitness(d1,d2,…,dN-1)}。 (8) WOA算法是一种随机的仿生优化算法,基于模仿座头鲸泡泡网猎食的反馈策略而形成的[22]。其数学模型主要有3个过程:包围目标、螺旋形泡泡网反馈策略和猎取目标。图1中,P是一个随机数,取值小于0.5,选择CSM(Circle Shrinking Machinism),反之,选择SUM(Spiral Uping Machnism)。a由2到0线性减小,r在[0,1]随机选取。WOA算法的流程图如图1所示。 图1 WOA算法的流程图 WOA算法的控制系数主要是A、C,控制参数相对较少,计算速度快效率高,易于实现。由于是一种新算法,目前应用研究基本没有,因此具有很大的应用前景。 通过2个实例来说明WOA方法的有效性和计算速度。第一个例子是利用WOA对限定孔径的线阵进行稀布化优化处理,以实现最低PSLL的阵元间距分布,另一个例子是对128阵元的阵列进行稀布化,实现在FNBW(First Null Beamwidth)限定的约束条件下以最少阵元取得最低的PSLL。仿真的硬件配置:主频2.66 GHz,内存2 GB,Matlab版本号为R2012b。 3.1 对37阵元的非均匀阵列稀布化 本例来自文献[3],以便于对比。考虑一个37阵元的中心对称阵列,半孔径的阵元个数则为18,设定阵元为各向同性,阵列间距不小于λ/2,根据原文献优化的数据,可以计算出阵列的孔径的尺寸为21.996λ。 依上所述,利用WOA算法,设定阵元的数目为37,则N=18,阵列的孔径尺寸限定为L=21.996λ,阵元间距de≥λ/2。 在此,WOA算法的基本参数设定:初始种群数目选为10,初始种群的产生采用均匀分布的随机数生成器,搜索空间的元素值的上界ub=1.5,下界lb=0.3。问题的优化维度为18,迭代的最大次数为300。 独立进行了10次仿真实验,WOA优化得到的阵元间距的仿真结果如表1所示,为了便于比较,文献[3-4]和文献[14]的优化结果也一并列出。 表1 阵元间距的优化结果对比 间距文献[3]文献[4]文献[14]WOA0~10.5000.5020.5000.5001~20.5000.5010.5000.5002~30.5000.5000.5000.5003~40.5000.5000.5000.5004~50.5000.5010.5000.5005~60.5000.5000.5000.5006~70.5000.5040.5000.5007~80.5000.5710.5000.5008~90.5890.5360.5000.5009~100.6330.5200.5000.50010~110.6640.5870.8090.80911~120.6870.5710.5880.58512~130.7070.7740.6380.63313~140.7220.7040.7460.74714~150.7351.0070.8840.88415~160.7460.8800.8930.89416~170.7540.8300.9220.92417~180.7610.50500.5150.518PSLL-19.415 -20.560 -20.627 -20.684 由表1可以看出,WOA与FLT、MGA、IPSO方法相比,取得了更低的PSLL,表明在旁瓣电平的压制方面WOA算法是行之有效的,并且WOA算法的每次优化只需要5 s的时间,非常快速,本文的硬件配置较低,在目前标准的硬件配置上优化会更快、用时更少。通过以上分析可以看出,WOA算法在本例的阵列的综合中收敛性能好,也是行之有效的综合方法。 WOA与FLT、MGA、IPSO方法的方向图如图2所示。为对比方便,沿y轴从下至上依次做了5 dB的偏移。 图2 WOA算法与其他算法的方向图 本例中最优和平均的迭代过程的收敛曲线如图3所示。可以看出,得到最优解的迭代过程中WOA算法能够快速的收敛到最优解,平均的迭代过程收敛曲线同样可以收敛迅速,说明WOA算法具有快速、稳健的特点。 图3 收敛曲线 3.2 对128阵元非均匀阵列的稀布化 在本例中,阵列的阵元数目为128,各向同性的阵元总体呈中心对称分布。约束条件是在稀布处理前后FNBW维持不变。在此,WOA算法的基本参数设定:初始种群数目选为10,初始种群的产生采用均匀分布的随机数生成器,搜索空间的元素值的上界ub=1.5,下界lb=0.3。问题的优化维度为18,迭代的最大次数为300,优化的维度依阵元个数而变。 优化的仿真试验共进行了10次。限于篇幅,表2列出了优化过程中4次的最优和最差的优化结果。 表2 4次优化过程中最优值与最差值的比较 运行次数阵元个数PSLL/dB孔径尺度运行时间/s1最优结果38-21.490517.8315λ28.25最差结果81-16.632756.2495λ28.342最优结果47-21.171923.5033λ28.71最差结果62-17.593326.2654λ28.453最优结果58-21.167225.1162λ28.13最差结果92-16.703175.4857λ28.694最优结果72-21.514645.988λ26.53最差结果32-19.405119.188λ7.11 从表2可以看出,最优结果的PSLL基本都在-21.2 dB左右,运行时间基本都在28 s左右,趋于稳定,FNBW在2°,最优的稀布结果是38阵元,阵元的填充率降低到30%,大大节约了功率,且PSLL还有一定幅度的再度压低。孔径尺寸最优的结果是17.831 5λ。在运行时间最小时,优化得到的阵元个数最小,但PSLL较大。 最优的稀布阵的方向图如图4所示。图4中画出了最优和最差的优化结果的方向图,为便于显示,最差结果沿y轴做了20的平移,FNBW保持在2°。4次迭代的最优结果的收敛曲线以及平均收敛曲线如图5所示。通过图4可以看到,最差结果的方向图旁瓣的幅度普遍高于最优结果的旁瓣幅度,最差结果的密集程度说明阵元总数目较大。 图4 最优稀布阵的方向图 图5 4次最优结果的WOA收敛曲线 由图5可以看出,收敛曲线几乎都在60次迭代左右即能到达最优值0.5 dB左右的搜索空间附近,并且收敛曲线走向基本一致,充分说明WOA算法收敛速度快,且具有强的稳健性。 针对一般随机搜索算法在非均匀稀布阵列的优化问题中计算代价较大的问题,尤其是在含有孔径约束、主波束宽度约束问题方面,将最新提出的WOA算法引入到这些问题的解决方案当中。本文利用WOA算法的随机搜索快速的特点,研究了在含有孔径约束和间距约束的双重约束情况下线阵的间距优化问题,构造出了相应合理的优化目标函数和适应度函数。在此基础上,进一步对较大规模阵列含有主波束宽度约束的问题进行了优化。由于WOA算法在随机搜索过程中过程的更新因子较少,避免了较为复杂的大量迭代运算过程,节省了内存空间和计算时间,在时间和空间的双重维度上实现了较大的性能优化,实用性和稳健性较高,具有较好的应用前景。 [1] BALANIS C A.Antenna Theory:Analysis and Design[M].New Jersey:Harper&Row,1982:989-990. [2] 薛正辉,李伟明,任武.阵列天线分析与综合[M].北京:北京航空航天大学出版社,2011:103-106. [3] KUMARB P,BRANN ER G R.Generalized Analytical Technique for the Synthesis of Unequally Spaced Arrays with Linear,Planar,Cylindrical or Spherical Geometry[J].IEEE Transactions on Antennas & Propagation,2005,53(2):621-634. [4] 陈客松,何子述,韩春林.非均匀线天线阵优化布阵研究[J].电子学报,2006,34,(12):2263-2267. [5] CEN L,YU Z L,SER W,et al.Linear Aperiodic Array Synthesis Using an Improved Genetic Algorithm[J].IEEE Transactions on Antennas & Propagation,2012,60(2):895-902. [6] HAUPT R L.Thinned Arrays Using Genetic Algorithms[J].IEEE Transactions on Antennas & Propagation,1994,42(7):993-999. [7] YUAN J,ZHOU H,GUO C,et al.Efficient Optimization of Shaped-beam Sparse Linear Antenna Arrays Using Genetic Algorithm[C]∥International Conference on Microwave and Millimeter Wave Technology,2012:1-4. [8] ZAMAN M A,MATIN M A.Nonuniformly Spaced Linear Antenna Array Design Using Firefly Algorithm[J].International Journal of Microwave Science & Technology,2012(5):408-412. [9] LI X,MA S,YANG G.Synthesis of Difference Patterns for Monopulse Antennas by an Improved Cuckoo Search Algorithm[J].IEEE Antennas & Wireless Propagation Letters,2016,151(16):141-144. [10] KURUP D G,HIMDI M,RYDBERG A.Synthesis of Uniform Amplitude Unequally Spaced Antenna Arrays Using the Differential Evolution Algorithm[J].IEEE Transactions on Antennas & Propagation,2003,51(9):2210-2217. [11] YAN K K,LU Y.Sidelobe Reduction in Array-pattern Synthesis Using Genetic Algorithm[J].IEEE Transactions on Antennas & Propagation,1997,45(7):1117-1122. [12] QUEVEDO-TERUEL O,RAJO-IGLESIAS E.Ant Colony Optimization in Thinned Array Synthesis with Minimum Sidelobe Level[J].IEEE Antennas & Wireless Propagation Letters,2006,5(1):349-352. [13] RAJO-IGLESIAS E,QUEVEDO-TERUEL O.Linear Array Synthesis Using an Ant-colony-optimization-based Algorithm[J].IEEE Antennas & Propagation Magazine,2007,49(2):70-79. [14] 刘姜玲,王小谟.改进粒子群算法综合有间距约束的稀布阵列[J].微波学报,2010,26(5):7-10. [15] 张建南,刘以安,王刚.基于优化粒子群算法的无人机航路规划[J].传感器与微系统,2017,36(3):58-61. [16] 王慧,王光宇,潘德文.基于改进粒子群算法的移动机器人路径规划[J].传感器与微系统,2017,36(5):77-79. [17] 侯大军,朱伟兴.基于改进粒子群算法的最优特征子集研究[J].传感器与微系统,2010,29(9):64-66. [18] OLIVERI G,MASSA A.Bayesian Compressive Sampling for Pattern Synthesis With Maximally Sparse Non-uniform Linear Arrays[J].IEEE Transactions on Antennas & Propagation,2011,59(2):467-481. [19] OLIVERI G,CARLIN M,MASSA A.Complex-weight Sparse Linear Array Synthesis by Bayesian Compressive Sampling[J].IEEE Transactions on Antennas & Propagation,2012,60(5):2309-2326. [20] OLIVERI G,WERNER D,BILOTTI F,et al.Reconfigurable Electromagnetics through Metamaterials[J].International Journal of Antennas and Propagation,2014(1):1-2. [21] NAI S E,SER W,YU Z L,et al.Beampattern Synthesis for Linear and Planar Arrays With Antenna Selection by Convex Optimization[J].IEEE Transactions on Antennas & Propagation,2011,58(12):3923-3930. [22] FUCHS B.Synthesis of Sparse Arrays With Focused or Shaped Beampattern via Sequential Convex Optimizations[J].IEEE Transactions on Antennas & Propagation,2012,60(7):3499-3503. [23] PRISCO G,D′URSO.M.Maximally Sparse Arrays via Sequential Convex Optimizations[J].IEEE Antennas & Wireless Propagation Letters,2012,52(11):192-195. [24] LEBRET H,BOYD S.Antenna Array Pattern Synthesis via Convex Optimization[J].IEEE Transactions on Signal Processing,1997,45(3):526-532. [25] MIRJALILI S,LEWIS A.The Whale Optimization Algorithm[J].Advances in Engineering Software,2016,95(4):51-67. SynthesisofNon-uniformLinearArrayAntennaBasedonWOA YUAN Peng-liang1,2,SHI Zhao3 (1.DepartmentofEnergyandEngineering,QingyangVocationalandTechnologyCollege,QingyangGansu745000,China; 2.SchoolofElectronicsandInformation,NorthwesternPolytechnicalUniversity,Xi’anShaanxi710129,China; 3.CollegeofElectronicEngineering,ChengduUniversityofInformationTechnology,ChengduSichuan610103,China) The WOA(whale optimization algorithm) is recently proposed as a new algorithm,which has promising application in the future due to its key characteristics of convenience and efficency.Research on this subject is not appear in public so far.In this paper,the application of WOA in synthesis of nonuniform linear array is described in detail,both in the sparsing of nonuniform linear array and in the supressing sidelobe level.The results show that WOA is effective on constraining synthesis of nonuniform sparse array,and outperforms other evolutionary algorithm such as GA and PSO in the characteristics of computing time and robust performance. WOA;synthesis of array;nonuniform linear array;sparsing 10.3969/j.issn.1003-3106.2017.10.12 袁鹏亮,史朝.WOA算法的非均匀稀布阵列优化方法[J].无线电工程,2017,47(10):53-58.[YUAN Pengliang,SHI Zhao.Synthesis of Non-uniform Linear Array Antenna Based on WOA[J].Radio Engineering,2017,47(10):53-58.] TN821 A 1003-3106(2017)10-0053-06 2017-06-11 国家自然科学基金资助项目(41505031);甘肃省高等学校科研基金资助项目(2016B-190)。 袁鹏亮男,(1980—),硕士研究生,在读博士,讲师。主要研究方向:阵列天线优化与逆向设计、RF通信。史朝男,(1981—),博士,副教授。主要研究方向:多普勒雷达信号信息处理。
min‖F(θ)‖,θ∈ΘS
s.t.
di-dj≥de>0,i,j∈z,
-N≤j2 WOA算法流程

3 实验结果及分析

4 结束语

