基于渐进均匀化理论的复合材料力学性能预测*
张延林, 姜雪光
(东北林业大学 机电工程学院, 哈尔滨 150040)
基于渐进均匀化理论的复合材料力学性能预测*
张延林, 姜雪光
(东北林业大学 机电工程学院, 哈尔滨 150040)
为了更好地预测复合材料的力学性能,以碳纤维增强木质复合材料为研究对象,建立了渐进均匀化理论的分析模型.利用小参数将宏、微观两尺度进行耦合,将以小参数渐进展开的力学变量代入单胞控制方程,最终推导出复合材料等效弹性模量的求解方程.采用ANSYS软件建立了复合材料的单胞模型,并在周期性边界条件下对弹性模量进行了预测分析.结果表明,与一般工程经验相比,渐进均匀化理论对复合材料的预测精度更高,且预测结果在一定范围内与物理实验结果吻合良好,验证了此理论的有效性.
渐进均匀化理论; 复合材料; 有限元; 单胞模型; 双尺度; 有效弹性模量; 平衡方程; 边界条件
复合材料是由两种或多种材料按一定规则经加工复合而成的新型材料,通过结合不同材料的特殊性可设计出理想的材料.复合材料在物理和化学方面具有诸多优点,因而广泛应用于各个领域.由于复合材料在结构和性能方面具有可设计性的特点,因此,复合材料制备前对材料性能进行预测具有现实意义[1].
为了更好地设计和优化复合材料,诸多专家学者提出了很多方法来对复合材料进行分析,如自洽法、代表体元法、有限元法[2]与均匀化方法等.自洽法一般用来分析结构较为简单的复合材料,对于具有复杂结构的复合材料其解析公式的推导十分复杂,运算量较大.代表体元法具有简单易行、适用范围广的特点,但和自洽法相比,缺少数学理论基础,因而通常用于近似解分析.20世纪70年代由Babuska[3]等提出的均匀化方法得到了极大发展.近年来许多专家学者对均匀化理论展开了研究工作.杨晓东[4]、刘贵立[5]等对颗粒增强复合材料的弹性模量进行了较为准确的预测.Cai[6]、蔡园武[7]等基于渐进均匀化理论对周期性板结构进行了分析,并对周期性板结构的弹性模量和正六角蜂窝板的等效刚度进行了预测.欧阳佳斯等[8]利用有限元分析法和ANSYS仿真软件对均一波纹单向复合材料板的力学性能进行了分析,并对其等效刚度进行了预测.张博明[9]、赵琳[10]等基于连续介质力学和均匀化方法对复合材料层合板进行了渐进损伤分析,并预测了该层合板的强度,其预测结果和实验值吻合较好.
本文将渐进均匀化方法应用于碳纤维增强木质复合材料的力学性能预测,利用有限元方法进行数学求解.解决了复合材料分析过程中高阶非线性化微分方程的计算问题.从周期性分布的单胞入手,将宏、微观变量利用小参数进行耦合.基于摄动理论,将位移变量进行小参数渐进展开并将其代入控制方程中,并推导出弹性模量的计算方程,从而能够分析宏、微观两尺度对材料力学性能的影响.在ANSYS软件中施加周期性边界条件,可以提高复合材料弹性模量的求解精度.通过与工程经验方程对比,可以验证本文方法的准确性.将预测结果与物理实验结果进行对比,并分析仿真值和实验值产生误差的原因.
1 实验方法
1.1 材料样板制备
主要实验原料包括短切碳纤维、木质纤维、脲醛胶粘剂、异氰酸树脂胶和固化剂等.选用木纤维与碳纤维两种预制材料.按照常规中密度纤维板的制板工艺进行样板制作.利用丙酮将异氰酸树脂胶黏剂稀释50%后,将其与碳纤维放入搅拌机中进行搅拌.异氰酸树脂胶具有化学稳定性,可以起到材料搭接作用,且不会对材料性能产生影响.搅拌一段时间后放入木纤维中,并将氯化铵与脲醛树脂胶黏剂混合均匀喷入搅拌机内.充分混合后将混合物放入预压机内进行预压,随后将其放入热压机内于175 ℃条件下热压7 min.将成型后的复合材料放入具有特定温度和湿度的环境中,直至温度和材料质量达到恒定.实验所得宏观样板如图1所示.图1a为普通木纤维(MDF)板,图1b~f为不同碳、木纤维质量比(F/M)下的碳纤维增强木质复合材料(SCFRW)板.

图1 实验所得宏观样板Fig.1 Macro sample templates obtained in experiments
1.2 材料性能测试
参照国家标准GB/T11718-2009,利用万能力学实验机测定碳纤维增强木质复合材料板的弹性模量,实验数据如表1所示.表1中,F为碳纤维质量,M为木纤维质量.
弹性模量计算公式为
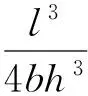
(1)
式中:l为支座间的距离;b为试件宽度;h为试件厚度;Δf为内力增加量;Δs为变形量.
2 渐进均匀化方法及有限元求解
渐进均匀化理论是利用渐进扩展和周期性假设来求解带有快速振荡参数的微分方程,该理论为预测复合材料的力学性能提供了理论思路,实质是利用均质宏观结构和非均质周期性分布的微观结构来描述原结构[3].SCFRW板(F/M=5∶10)的宏、微观形貌如图2所示.一般情况下材料在宏观上表现为均质性(见图2a),在微观上呈现非均质性(见图2b).
基于周期性假设的复合材料微观结构和单胞如图3所示.与材料的宏观几何尺度相比,单胞尺度是很小的量,这里用小参数ε(0<ε≪1)来代表单胞特征尺寸.引入宏观尺度变量x和微观尺度变量y,则小参数为宏观变量和微观变量的比值,即ε=x/y.将位移场量u以ε作渐进级数展开,得到关于宏观变量和微观变量的位移场函数,其表达式为

表1 实验数据Tab.1 Experimental data MPa

图2 复合材料的宏、微观形貌Fig.2 Macro and micro morphologies of composite
u(x)=u(x,y)=u0(x,y)+εu1(x,y)+ε2u2(x,y)+Ο(ε3)
(2)
式中:u0(x,y)、u1(x,y)和u2(x,y)分别为第一、二和三项基底函数;O表示高阶无穷小,计算时趋近于0.
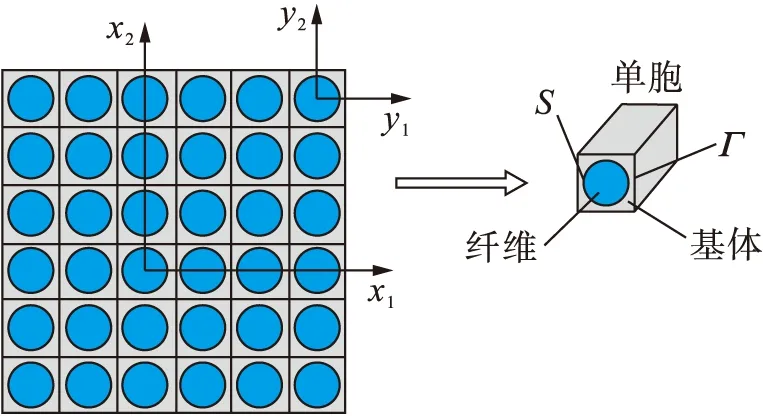
图3 周期性排列的微观结构及单胞Fig.3 Periodically arranged microstructure and unit cell
在弹性理论中根据虚位移原理可以得到胞元控制微分方程为
(3)
式中:Eijkl为4阶弹性张量,下标i、j、k和l用以区分不同方向的坐标变量,根据下标取值不同,Eijkl可以表示不同方向的弹性模量;wi为满足固定边界条件的任意虚位移;Ω为材料的基体部分参量;Γ为单胞边界参量;S为碳纤维的边界参量;fi、ti和pi分别为加载在胞元上的体积力、面积力和张力.
将位移场函数代入弹性理论的控制微分方程中,并令关于小参数ε具有相同阶数的项相等,即可得到一系列摄动方程,对这些方程进一步求解可以得到u0(x,y)、u1(x,y)与宏观尺度结构的总体平衡方程分别为
u0(x,y)=u0(x)
(4)
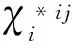
(5)
(6)
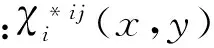
周期结构单胞的等效弹性模量为
(7)
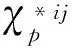
可以通过有限元方法求解等效弹性模量.实际求解过程中的关键步骤是求取特征位移.在有限元分析中需要对单胞施加载荷与周期性边界条件,再对特征位移进行求解.
3 复合材料的ANSYS仿真
3.1 周期性边界条件
在均匀化理论中微观结构的周期性分布是该理论的重要假设.采用ANSYS软件进行单胞模型有限元分析时,为了提高计算精度,需要保证单胞边界上的位移和应力连续.本文采用Xia等[11]提出的周期性边界条件,则单胞内的节点位移场可表示为
(8)
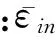
在三维周期性排列的单胞模型中,对称边界上的位移场相减则可消去位移修正量,即
(9)
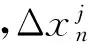
3.2 弹性模量
基于上述分析,采用有限元分析软件ANSYS对微观单胞上各节点的弹性模量进行求解.首先建立微观单胞模型,利用Solid186单元对单胞模型进行网格划分,则网格划分后的单胞模型如图4所示.

图4 网格划分后的单胞模型Fig.4 Unit cell model after grid meshing
利用渐进均匀化方法进行节点弹性模量的求解.首先对特征位移进行求解.对单胞z方向的节点施加单位位移载荷,对其求解可得单位节点反力.随后对单胞施加周期性边界条件,将得到的单位节点反力施加到单胞节点上,经求解后即可得到特征位移,其等值线分布如图5所示.其次对特征节点反力进行求解.将求解得到的特征位移继续施加到周期性边界条件下的单胞节点上,经过ANSYS计算后即可得到特征节点反力.应力的等值线分布与应力云图分别如图6、7所示.观察图6、7可知,当对单胞施加均匀应变时,碳纤维的应力值大于基体应力值,且碳纤维承受了复合材料形变中的主要应力.因此,碳纤维的加入大大提高了复合材料的力学性能.
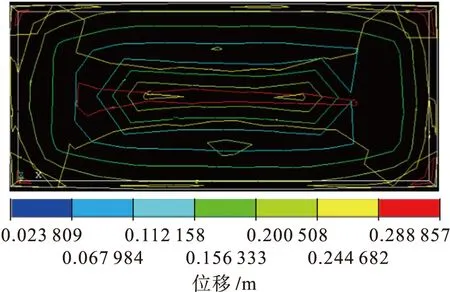
图5 特征位移的等值线分布Fig.5 Isoline distribution of characteristic displacement
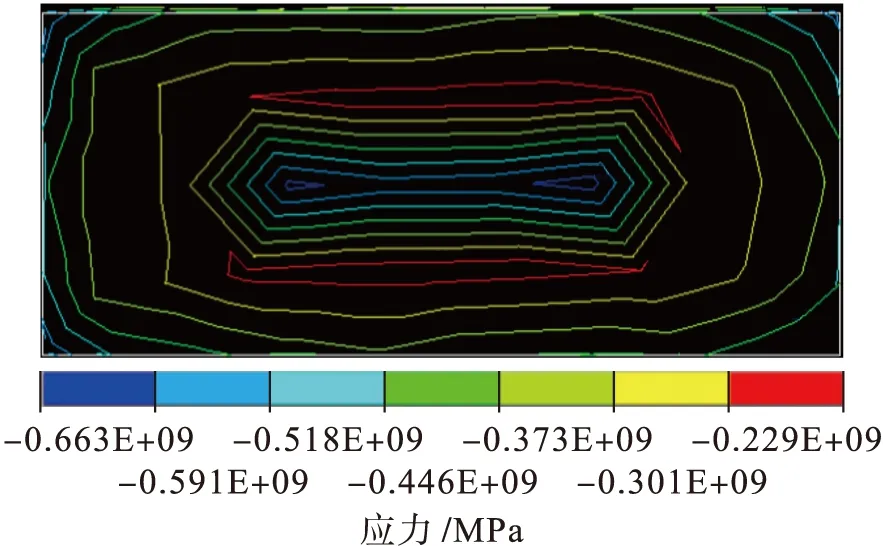
图6 应力的等值线分布Fig.6 Isoline distribution of stress
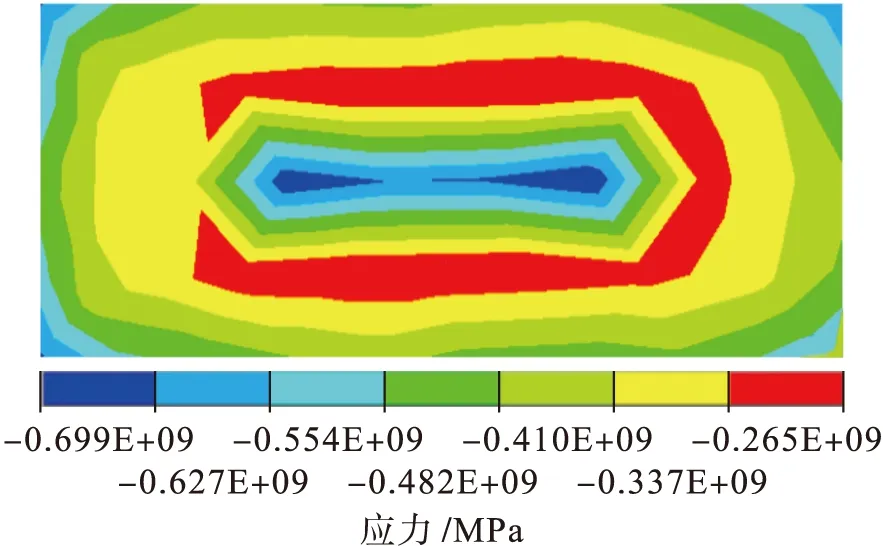
图7 应力云图Fig.7 Nephogram of stress
利用求解得到的特征位移和特征节点反力计算弹性模量.将得到的单元节点数据进行提取并整理坐标信息,采用MATLAB软件中的单元组装函数Assembly对数据进行整合,得到的弹性模量如表2所示.介于实验数据限制,本文只求解了垂直于板面的弹性模量.

表2 不同方法测得的弹性模量Tab.2 Elastic modulus measured with different methods MPa
为了验证本文方法在进行复合材料分析时的有效性和准确性,采用工程经验公式对本文结果进行对比分析.垂直于碳纤维轴向的等效弹性模量的经验公式为
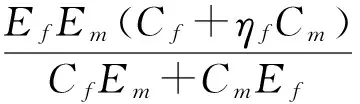
(10)
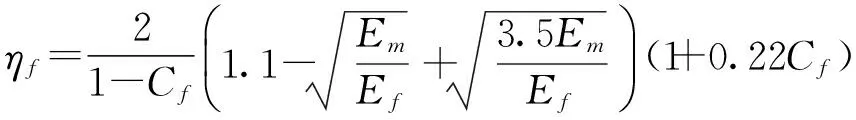
(11)
式中:Ef为碳纤维的弹性模量,且Ef=228 GPa;Em为基体的弹性模量,且Em=1.5 GPa;Cf为碳纤维体积分数;Cm为基体体积分数.
图8为复合材料弹性模量对比结果.观察图8可知,当复合材料的碳、木纤维质量比(F/M)小于0.3时,渐进均匀化方法的计算误差率为0.051 1~0.178 8,工程经验法的计算误差率为0.263 8~0.308 0,此时渐进均匀化方法的计算精度明显高于工程经验法.当复合材料的碳、木纤维质量比高于0.3时,渐进均匀化方法和工程经验法的计算误差率将随碳、木纤维质量比的增大而增大,此时两种方法均不再适用.
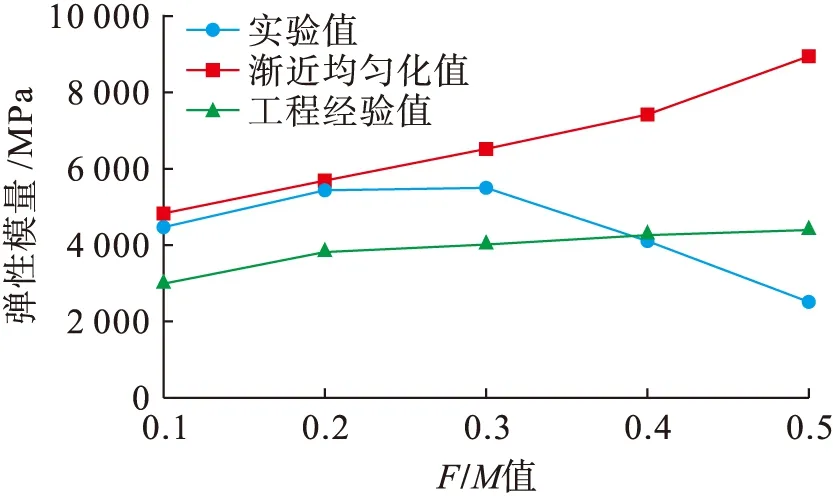
图8 复合材料弹性模量对比Fig.8 Comparison in elastic modulus of composites
另外,观察表1中的内结合强度数据可知,随着碳纤维含量的增加,碳纤维与基体的结合强度逐渐降低,可以认为内结合强度的降低是导致复合材料性能下降的主要因素.同时,由图6、7可见,纤维和基体的接触面应力小于纤维和基体本身的应力,这种现象进一步验证了上述分析.由于渐进均匀化方法未考虑到内结合强度的影响,在一定范围内导致预测值比实验值略高.由表1可知,当普通木纤维板中加入碳纤维后(F/M=1∶10),材料的弹性模量由1 626.64 MPa增加到4 442.72 MPa,静曲强度由14.73 MPa增加至31.71 MPa,材料的整体力学性能大幅度提高.观察表1还可以发现,随着碳纤维含量的增加,材料的力学性能逐渐增高.当碳、木纤维质量比为3∶10时,材料性能出现峰值,之后随着碳纤维含量的增加,材料的性能随之降低.因此,在复合材料的制备过程中,并非碳纤维掺杂量越多,材料性能越好.合理分配碳、木纤维的质量比是设计出具有良好性能的复合材料的关键.
4 结 论
本文利用ANSYS大型有限元分析软件,基于渐进均匀化理论与有限元方法,实现了对复合材料弹性性能的预测与分析.进均匀化理论具有严格的数学理论基础.一般估算分析方法(如代表体元法、工程经验法等)虽然计算简单但预测精度较低.本文在ANSYS仿真环境中建立了微观单胞模型,利用MATLAB软件计算材料的弹性模量,大大简化了计算难度.通过以上实验分析可以得到如下结论:
1) 仿真数据在一定范围内和实验值吻合良好,验证了本文方法的有效性.
2) 基于周期性假设,本文方法虽然降低了一定的计算精度,但大大降低了解析法的计算复杂度.
3) 本文为复合材料设计提供了一定的参考价值.复合材料的制备应合理地分配纤维与基体的质量比.根据仿真分析得到的特征位移与应力等值线分布以及应力云图,可以更好地分析材料的微观结构受力特征,同时也便于分析材料的应力集中问题.
4) 本文方法的不足之处在于忽略了内结合强度对材料力学性能的影响,导致仿真结果和实验数据存在一定误差.
[1] 刘树良,陈涛,魏宇祥,等.碳纤维增强复合材料加工技术研究进展 [J].航空制造技术,2015(14):81-86.
(LIU Shu-liang,CHEN Tao,WEI Yu-xiang,et al.Research progress in processing technology of carbon fiber reinforced composites [J].Aeronautical Manufacturing Technology,2015(14):81-86.)
[2] 张超,许希武,许晓静.三维多向编织复合材料宏细观力学性能有限元分析研究进展 [J].复合材料学报,2015,32(5):1241-1251.
(ZHANG Chao,XU Xi-wu,XU Xiao-jing.Research progress in finite element analysis on macro-meso mechanical properties of 3D multi-directional braided composites [J].Acta Materiae Compositae Sinica,2015,32(5):1241-1251.)
[3] Babuska I.Homogenization approach in engineering [J].Computing Methods in Applied Sciences and Engineering,1976,134:137-153.
[4] 杨晓东,董泽民,杨坤,等.颗粒增强复合材料弹性结构的双尺度有限元分析 [J].机械工程学报,2012,48(8):34-38.
(YANG Xiao-dong,DONG Ze-min,YANG Kun,et al.Two scale analysis of elastic structures of particle reinforced composite materials with finite element method [J].Journal of Mechanical Engineering,2012,48(8):34-38.)
[5] 刘贵立,赵明明,董驾潮,等.基于 ANSYS 的颗粒增强镁基复合材料应力场分析 [J].沈阳工业大学学报,2015,37(1):44-48.
(LIU Gui-li,ZHAO Ming-ming,DONG Jia-chao,et al.Stress field analysis for particle reinforced magnesium matrix composites based on ANSYS [J].Journal of Shenyang University of Technology,2015,37(1):44-48.)
[6] Cai Y,Liu X,Cheng G.Novel numerical implementation of asymptotic homogenization method for periodic plate structures [J].International Journal of Solids and Structures,2014,51(1):284-292.
[7] 蔡园武,徐亮,程耿东.正六角形单胞周期性蜂窝板等效刚度研究 [J].大连理工大学学报,2014,54(4):377-383.
(CAI Yuan-wu,XU Liang,CHENG Geng-dong.Study of effective stiffnesses of periodic honeycomb plate with regular hexagonal unit cell [J].Journal of Dalian University of Technology,2014,54(4):377-383.)
[8] 欧阳佳斯,倪爱清,朱俊,等.均一波纹单向复合材料板的力学性能研究 [J].玻璃钢/复合材料,2016(3):38-43.
(OUYANG Jia-si,NI Ai-qing,ZHU Jun,et al.The mechanical behavior of unidirectional composite lamina with uniform waviness [J].Fiber Reinforced Plastics/Composites,2016(3):38-43.)
[9] 张博明,赵琳.基于单胞解析模型的复合材料层合板渐进损伤数值分析 [J].工程力学,2012,29(4):36-42.
(ZHANG Bo-ming,ZHAO Lin.Numerical analysis for progressive damage of composite laminates based on analytic model of unit cell [J].Engineering Mechanics,2012,29(4):36-42.)
[10]赵琳.基于单胞解析模型与渐进损伤分析的复合材料强度预报 [D].哈尔滨:哈尔滨工业大学,2012.
(ZHAO Lin.Strength prediction of composites based on unit cell analytic model and progressive damage analysis [D].Harbin:Harbin Institute of Technology,2012.)
[11]Xia Z H,Zhou C W,Yong Q L,et al.On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites [J].International Journal of Solids and Structures,2006,43(2):266-278.
[12]张超,许希武,严雪.纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现 [J].航空学报,2013,33(7):1636-1645.
(ZHANG Chao,XU Xi-wu,YAN Xue.General perio-dic boundary conditions and its application on micro-mechanical finite element analysis of textile composites [J].Acta Aeronautica et Astronautica Sinica,2013,33(7):1636-1645.)
(责任编辑:尹淑英 英文审校:尹淑英)
Mechanicalpropertypredictionofcompositesbasedonasymptotichomogenizationtheory
ZHANG Yan-lin, JIANG Xue-guang
(College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China)
In order to effectively predict the mechanical properties of composites, the carbon fiber reinforced wood composites were taken as the study object, and the analytical model based on the asymptotic homogenization theory was established. The macroscopic and microscopic scales were coupled with small parameters, the mechanical variables asymptotically expanded with the small parameters were substituted into the control equations of unit cell, and the solution equations of equivalent elastic modulus of composites were finally derived. The unit cell model for the composites was established with the ANSYS software, and the elastic modulus was predicted and analyzed under the periodic boundary conditions. The results show that compared with the general engineering experience, the asymptotic homogenization theory has more accurate prediction accaracy, and the prdicted results are in good agreement with the physical experimental results in a certain range, which verifies the effectiveness of the theory.
asymptotic homogenization theory; composite; finite element; unit cell model; double scale; effective elastic modulus; equilibrium equation; boundary condition
TB 332
: A
: 1000-1646(2017)05-0507-06
2017-04-10.
黑龙江省留学归国科学基金资助项目(LC201408).
张延林(1970-),男,山东招远人,副教授,硕士,主要从事复合材料计算机控制等方面的研究.
* 本文已于2017-08-01 12∶24在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20170801.1224.018.html
10.7688/j.issn.1000-1646.2017.05.06

