基于差分插补原理的多维线性空间插补与仿真*
王宏甲,赵庆志,乔磊,杨召彬,吴俊杰
(山东理工大学 机械工程学院,山东 淄博 255000)
基于差分插补原理的多维线性空间插补与仿真*
王宏甲,赵庆志,乔磊,杨召彬,吴俊杰
(山东理工大学 机械工程学院,山东 淄博 255000)
为了实现采用差分插补原理的数控系统能够进行多维线性空间插补,以平面直线插补为基础,对差分插补原理进行了再研究。从差分插补原理的基准轴与非基准轴进给判定中,找到了实现基于差分插补原理的多维线性空间插补的关键点。通过对多维线性插补的分析,给出了多维线性插补的具体流程及其差分代码的初始化,实现了基于差分插补原理的多维线性空间插补。该插补方法简单可行,易于实现多轴控制。通过空间直线插补实例分析以及刀具路径的插补仿真,进一步说明了基于差分插补原理的多维线性空间插补方法能够满足空间多维数控加工的要求。
差分插补原理;多维线性空间插补;路径仿真
0 引言
插补运算是数控系统最重要的计算任务。插补程序的计算效率和计算精度是衡量数控系统性能的重要指标[1]。在以步进电机为驱动装置的经济型数控系统中,插补方法主要有逐点比较法、数字积分法以及比较积分法等[2]。这些方法不但在平面加工中得到了广泛的应用,而且在多轴联动机床的空间插补加工中也发挥了重要的作用。尤其是在数控机床的升级改造过程中,多轴联动机床的迅速普及,要求经济型数控系统的插补算法能够适应多轴联动加工的基本要求,满足现代化生产的需要[3]。
在上世纪80年代,王敏教授深入分析国内外数控插补技术,从理论上开创性地研究了适合变量可分离的正高次曲线数控加工的差分插补原理。该插补方法具有插补功能强大,控制精度高,操作使用容易等优点[4]。近年来,赵庆志[5-8]、单东日[9]等学者对该方法进行了深入的研究,实现了直线以及圆锥曲线采用统一运算框图的直接插补,使数控系统的插补功能有了极大的改善。现阶段,以差分插补原理为核心的数控机床主要进行平面内复杂轮廓的加工,但是对于空间直线的插补则力不从心,没有进行深入研究。在这种情况下,采用差分插补原理的数控机床进行空间直线插补时,还需辅以其他插补方法,比如DDA法等。这就使得数控系统更加复杂,增加了数控系统的开发难度。
为了适应数控加工发展的需要,针对上述情况,本文将对拥有较强平面插补功能的差分插补原理进行再研究,以期应用该插补方法实现多维线性插补,丰富差分插补原理的应用,满足现代化加工的需要。
1 采用差分插补原理的平面直线插补
1.1 差分插补原理简述
差分插补原理能够实现对变量可分离的正高次曲线的直接插补。该原理是从原点开始,依据函数递增的趋势进行推导。为满足插补的理论依据,曲线方程需经坐标系平移和变向化为可分离变量的正高次曲线。从而,建立以曲线加工起点为坐标原点,起点处沿加工方向的切线在第一象限的“相对坐标系”,并求出该坐标系下x,y的各阶差分。
在插补的过程中,每进给一次之前,需先比较一下x,y一阶差分值的大小,取一阶差分值较小的坐标轴为基准轴。在每一次进给中,基准轴均进给一步。非基准轴的进给取决于函数值偏差与非基准轴的一阶差分值相比较的结果。当偏差值超过非基准轴一阶差分值一半时,两轴同时进给才能保证误差最小。此时,进给的实际误差不会超过半个脉冲当量[4]。
1.2 平面直线差分插补代码的初始化
将在平面直角坐标系中用ISO代码定义的直线方程,按照坐标平移和变向化为相对坐标系中的正一次曲线方程,其形式为:
a1y=b1x
则其差分插补代码为:
jx1,jy1,F,G,jj,L
各代码含义为:
jx1:x的一阶差分;jy1:y的一阶差分;
F:插补偏差;G:计数方向;
jj:曲线在x轴(或者y轴)上的投影长度;
L: 机床绝对坐标象限。
其中,jx1=b1,jy1=a1,在插补的过程中,必须保证jx1>0,jy1>0,其具体差分计算见相关参考文献[4]。F为插补偏差,F=P1(x)-Q1(y)或者F=Q1(y)-P1(x),在插补初始化时,F=0。G为计数方向,用来判断投影方向。若曲线终点的切线斜率绝对值K大于1时,G=Gy,曲线的投影方向为y轴,否则G=Gx,曲线的投影方向为x轴。jj为曲线在投影方向上的计数长度。L为曲线加工起始段所在的机床绝对坐标系象限号。
2 采用差分插补原理的多维线性插补
由上文分析知,差分插补原理以脉冲密度高的轴作为基准轴。在每一次插补进给中都要包含基准轴,并判断非基准轴的脉冲是否存在。本文将以此为基础,将平面直线插补扩展到空间多维线性插补。
2.1 差分插补原理的多维线性插补分析
设有多维函数满足:
X:Y:Z:θ=a:b:c:d
为方便分析,假设a,b,c,d均为正数,且a的值最大。将上述多维线性函数化为变量可分离的形式并求得X,Y,Z,θ的一阶差分:
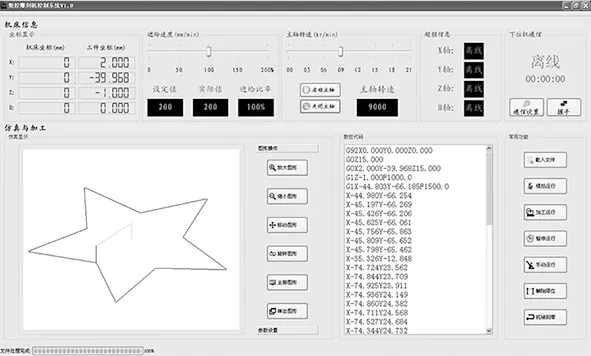
由于jx1 由多维线性插补原理[12]可知,在插补的过程中,各轴的进给方向不发生变化,不存在过象限的问题。所以在进行插补之前,通过程序开辟专门的内存空间来存储各个轴的进给方向。在插补的过程中,坐标参数均采用绝对值的形式进行插补运算。通过这一措施,就将多维线性插补的全部情况都纳入到上述分析中,从而避免了各个象限的判断计算,简化了插补程序,提高了插补计算的效率。 2.2 多维线性差分插补流程及插补代码初始化 在相对坐标编程模式下,有多维线性插补指令G01(a,b,c,…d)。 由上文分析可知,本文提出的基于差分插补原理的多维线性插补流程如下: 有了校园创作的体验,学生兴致更高。我顺势把学生带到玄武湖。这是这次校本选修课给我感受最深的一次活动。我们总结了校园创作的经验,又做了一些改进,每到一个景点,要求学生展开竞赛,谁对得快,谁对得好,就给谁奖励。小小的激励机制,使得学生情绪更加高涨,才思更加敏捷。面对一处处景点,佳联叠出,引得游人驻足,赢得啧啧称赞。 (1)根据坐标值的正负,判断各轴的进给方向。 (2)对各坐标值取绝对值,令Max等于最大的绝对值。 (3)差分插补代码初始化: 计算各轴的一阶差分值,即jx1=|Max/a|, jy1=|Max/b|,jz1=|Max/c|… 令各轴偏差等于0,即Fx=0,Fy=0,Fz=0… 插补循环次数jj=Max (4)确定基准轴的一阶差分值,即各轴一阶差分值中的最小值。 (5)进行差分插补运算。 由于线性插补不存在过象限问题,所以本文设计的多维线性差分插补不再考虑G、L参数,减少了插补参数的计算,简化了插补流程,提高了插补计算的效率。为了保证插补运算的实时性,上述流程的前四步,都将在译码阶段完成。差分插补运算的具体流程,如图1所示。 为方便分析,现以加工起点为坐标原点O(0,0,0),终点为E(6,5,3)的空间直线段OE为例。使用文中的多维线性差分插补算法进行插补计算,其插补过程及计算数据如表1所示。 表1 空间直线插补过程以及计算数据 利用计算机进行刀具路径的插补仿真是验证插补算法正确性的重要途径。为进一步验证本文提出的多维线性空间插补方法,本文在OpenGL渲染环境中进行刀具路径的插补仿真显示模块开发。刀具路径的显示模块,是将插补计算提供的数据转换为屏幕上显示的刀具路径,实现刀具路径的多维线性空间插补仿真。 由多维线性插补与数控加工原理可知,空间复杂曲线的加工是由各直线轴与旋转轴沿各自轴线加工运动复合而成。采用计算机进行刀具路径仿真加工时,可将空间点依次绕各个轴线旋转,然后投影到二维计算机屏幕上进行显示。 由计算机图形学中的三维几何变换[13]可知,在右手笛卡尔坐标系中,设绕坐标轴的旋转角为β,则绕x轴的三维旋转变化矩阵为: 绕y轴的三维旋转变化矩阵为: 绕z轴的三维旋转变化矩阵为: 在仿真插补运算的过程中,将插补程序计算出的多维坐标数据,依次带入到各轴的旋转变化矩阵中进行计算,最后将得到的二维平面数据传到OpenGL中进行显示,即可实现刀具路径的多维线性空间插补仿真。本文采用上述方法,开发的数控雕刻机控制系统界面如图2所示。 图2 数控雕刻机控制系统界面 通过CAD/CAM软件[14],对灰度图片进行自动化编程,将生成的G代码导入到本文开发的数控雕刻机控制系统中进行空间直线的仿真测试,仿真结果如图3所示。 图3 空间直线插补仿真 在对旋转轴插补仿真测试中,加工路径为起点(0,0,5),绕Y轴旋转加工5圈,到达终点(0,30,10)的圆锥形螺旋线,其仿真结果如图4所示。 图4 绕Y轴圆锥形螺旋线加工仿真 本文通过对差分插补原理的分析,将平面直线插补扩展到空间多维线性插补,拓展了差分插补原理的应用范围,实现了平面圆锥曲线与多维线性插补方法的统一,为后期开发基于差分插补原理的多轴数控雕刻机控制系统奠定了良好的基础。 [1] 李彦奎,吕彦明. 时间分割圆弧插补算法的改进[J]. 组合机床与自动化加工技术, 2017(1):16-18. [2] 王永章. 机床的数字控制技术[M]. 哈尔滨:哈尔滨工业大学出版社, 2015. [3] 李珑. 发展经济型数控系统的必要性探究[J]. 经济研究导刊, 2017(6):175-176. [4] 王敏.差分插补方法及其在数控线切割机中的应用(一)[J].电加工,1981(4):16-22. [5] 赵庆志. 基于可重构理论的慢走丝线切割机床控制系统研究与设计[D].南京:南京航空航天大学, 2005. [6] 赵庆志,谭培红,高振华. 抛物线ISO代码译成差分插补代码及其实现[J]. 机械设计与制造,2006(5): 57-59. [7] 刘肖,赵庆志,于光伟,等. 双曲线ISO代码译成差分插补代码及程序的实现[J]. 山东理工大学学报(自然科学版),2010,24(2):82-86. [8] 王宜龙,赵庆志,王海涛. 椭圆ISO代码译成差分插补代码及其程序的实现[J]. 机床与液压,2009,37(9): 54-55,118. [9] 单东日. 基于二次代数样条差分插补的平面参数曲线数控加工[J]. 制造技术与机床, 2009(2):95-98. [10] 单东日,王涛. 圆锥样条合成矢量插补及C机能刀补[J]. 机械科学与技术, 2010, 29(1):68-71. [11] 王涛. 圆锥样条合成矢量插补及C机能刀补[D]. 济南:山东轻工业学院, 2010. [12] 吴黎明. 数字控制技术[M].北京:科学出版社, 2009. [13] 赫恩,巴克,卡里瑟斯. 计算机图形学[M]. 蔡士杰,杨若瑜,译. 北京:电子工业出版社, 2014. [14] 韩式国,赵军,陈晓晓,等. 数控编程技术及其典型应用研究[J]. 组合机床与自动化加工技术,2012(3):100-103. (编辑李秀敏) MultidimensionalLinearInterpolationandSimulationBasedonDifferenceInterpolationTheory WANG Hong-jia,ZHAO Qing-zhi,QIAO Lei,YANG Zhao-bin ,WU Jun-jie (School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255000, China) In order to realize multidimensional linear interpolation of NC system with differential interpolation theory, the theory of differential interpolation is further studied by researching on plane linear interpolation. The key points to realize the multidimensional linear interpolation based on the difference interpolation theory are found from the determination of the feed of the basic axis and the non basic axis in the differential interpolation theory. Multidimensional linear interpolation with differential interpolation theory is realized by the determination of multidimensional linear interpolation process and its differential code. The interpolation method is simple and feasible, and it is easy to realize multi axis control. Further more, it can meet the requirements of space multidimensional NC machining by the analysis of spatial linear interpolation case and interpolation simulation of tool path. differential interpolation; multidimensional linear interpolation; simulation of path TH162;TG659 :A 1001-2265(2017)09-0012-04 10.13462/j.cnki.mmtamt.2017.09.004 2017-05-11 山东省自然科学基金资助项目(ZR2016EL13) 王宏甲(1988—),男,山东潍坊人,山东理工大学硕士研究生,研究方向为数控技术与装备,(E-mail)whj1988928@163.com;通讯作者:赵庆志(1962—),男,山东日照人,山东理工大学教授,博士,研究方向为数控技术与装备、机电一体化技术,(E-mail)zhaoqzme@163.com。3 空间直线插补实例分析
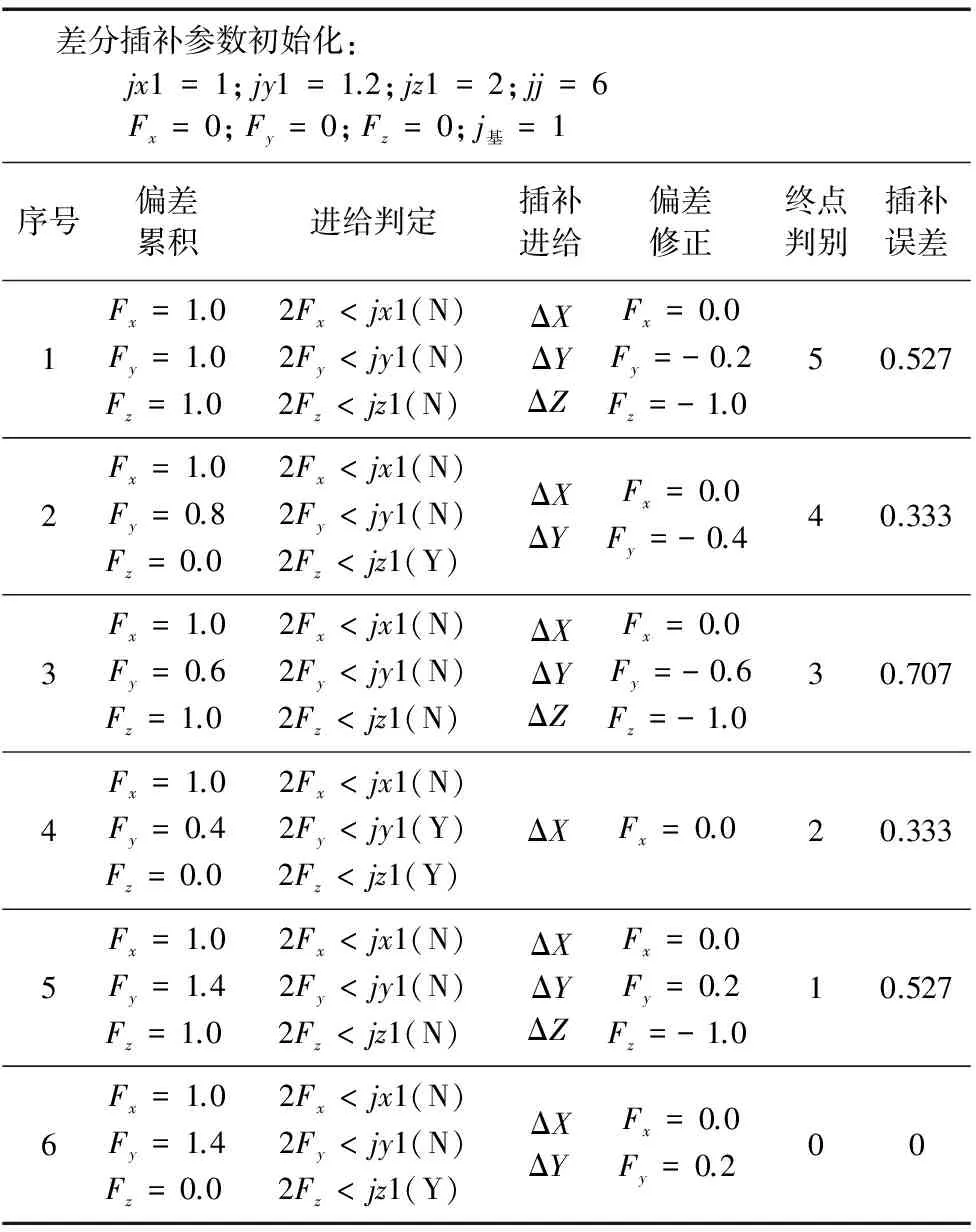

4 刀具路径的多维线性空间插补仿真


5 结束语

