风力机叶片设计方法的研究*

徐凯,吴东垠

(西安交通大学 能源与动力工程学院，西安 710049)

风力机叶片设计方法的研究*

徐凯,吴东垠**

(西安交通大学 能源与动力工程学院，西安 710049)

研究了经典动量-叶素理论和修正后的动量-叶素理论两种风力机叶片设计方法并进行了比较，对修正的动量-叶素理论计算的参数进行拟合，以某型号风力机为例，运用Matlab编程功能，引用设计范围更广的风力机翼型专用软件XFOIL，研究表明：拟合前后的弦长和扭角差异主要在靠近叶根部分；修正的动量-叶素理论相对于经典动量-叶素理论计算的轴向诱导因子，主要区别在于叶根和叶尖部分，切向诱导因子的影响非常小。

动量-叶素理论；叶片设计；Matlab

风力机叶片是风力机主要的吸收风能装置，风力机叶片气动设计则是整个风力机设计过程中最关键的部分，其性能的好坏直接影响整个风力机的效率[1-2]。目前风力机叶片设计的主要方法有经典BEM法和修正后的Glauert法、Wilson法、Zchmitz法等[3]，文献在设计风力机叶片时，只考虑修正后的方法，对于修正理论相对于经典理论计算的参数，尤其是弦长、扭角、轴向诱导因子、切向诱导因子等，在数字与图形方面，没有对比体现，缺少直观性，且传统的翼型设计软件Profili只针对有限的固定参数，适用面窄，对于上述问题，本文在传统的设计理论下，根据风力机运行实况，把气流通过叶尖的损失、叶片宽度和厚度对攻角的影响、失速修正对气动参数的影响考虑进来，引用设计范围更广的风力机翼型专用软件XFOIL，通过图形形式直观地体现修正后的参数相对于经典理论的差异，指出叶片具体部位的修正，对工程人员在设计风力机叶片时提供技术支撑。

1 基本理论

1.1 经典设计理论

由叶素理论有

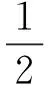
(1)

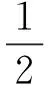
(2)

其中：

CT=CLsinφ-CDcosφ

(3)

CN=CLcosφ+CDsinφ

(4)

其中，dFT为法向力(N)；dFN为切向(N)；FL为升力(N)；FD为阻力(N)；φ为入流角(°)；ρ为密度(kg/m3)；w为合速度(m/s)；C为弦长(m)；dr为叶片展长(m)；CT为法向系数(N)；CN为切向系数(N)。

则轴向气动力和气动转矩分别为

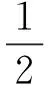
(5)

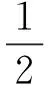
(6)

其中，B为叶片个数。

由动量理论有

(7)

dM=4πρr3U1(1-a)Ωbdr

(8)

其中，U1为来流速度(m·s-1)；Ω为旋转角速度(rad·s-1)。

由动量-叶素理论(BEM)有

dN叶=dN动dM叶=dM动

(9)

整理后得

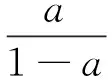
(10)

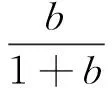
(11)

b(1+b)λ2=a(1-a)

(12)

(13)

θ=φ-α

(14)

dP=ΩdM=4πρr3Ω2b(1-a)U1dr

(15)

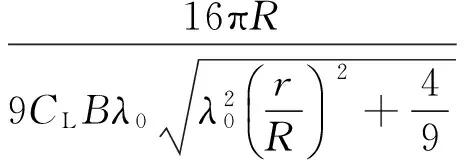
(16)

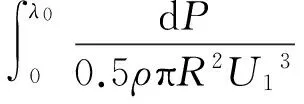
(17)

其中，a为轴向诱导因子；b为切向诱导因子；σ为实度，等于BC/2πr；λ为叶尖速比，等于ΩR/U1。

1.2 修正的动量-叶素理论

由动量-叶素理论计算的参数值与实际运行的风力机叶片有一定的偏差，所以需要对动量-叶素理论进行修正，本文主要考虑以下修正内容：气流通过叶尖的损失、叶片宽度和厚度对攻角的影响和失速修正对气动参数的影响。

1.2.1 叶尖损失的影响

由于叶片吸力面的压力小于压力面的压力，空气趋于从下表面绕过叶尖流向上表面，从而减小了叶尖附近的升力和功率，因此需要考虑叶尖损失因子[4]。

(18)

此时，方程变为

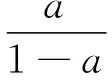
(19)

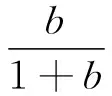
(20)

1.2.2 叶栅理论

在翼型的性能计算中，攻角是一个非常重要的影响因素，它直接影响翼型的升力与阻力系数。由于叶片有一定的弯度与厚度，将会对叶素的轴向和切向速度产生影响，在翼型头部和尾部，气流的切向速度增加，同时由于翼型厚度减小了流道尺寸，流体的轴向速度增加。叶栅的这一影响可称为叶栅效应，对攻角的影响可用以下公式来描述[5-6]。

(21)

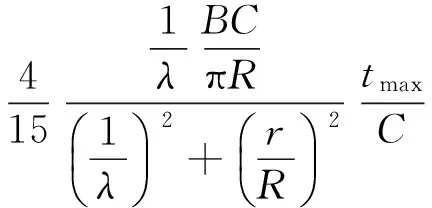
(22)

Δα=Δα1+Δα2

(23)

其中，Δα1为叶片宽度影响量；Δα2为叶片弯度影响量。

1.2.3 失速修正

当轴向因子a>0.353 9时，风力机处于非常复杂的湍流流动中，承受很大的载荷，动量定理不再适应，风力机通常处于失速状态，因此要对流动进行修正[7]。

(24)

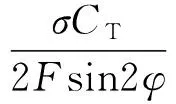
(25)

则有

(26)

(27)

其中

H=1.0a≤0.353 9

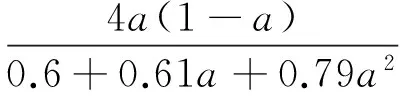
1.3 翼型的选取

在风力机的所有结构设计中，翼型是风力机叶片最主要的组成部分，风力机的发电过程就是将风能通过捕风装置转化为机械能，再将机械能转化为电能[8]，因此构成风轮的翼型将直接影响风力机的效率。在翼型选取过程中，要使所选翼型具有最大升阻比。早期的风力机翼型一般都使用传统的航空翼型，主要原因在于其拥有大的升阻比，航空翼型主要有NACA系列、fx系列、s系列等型号[9]。考虑到制造方便，本文统一采用NACA4415翼型。

XFOIL软件是美国麻省理工学院马克·雷拉博士于1986年开发的一款专用于翼型设计与计算的互动式程序[10]，在小攻角范围内计算出来的翼型参数和实验数据相比，误差非常小。将所选翼型数据导入到xfoil中，在接近实际运行的雷诺数下，经过多次迭代计算，最终得到最大升阻比下的最佳攻角为α=70，升力系数CL=1.178 1,阻力系数CD=0.011 53，最大升力系数CL=1.528，最大升阻比CL/CD=102.176 9。

2 算例分析

以某型号5 kW风力机为例进行分析，应用Matlab工程数值计算软件进行编程计算，通过计算，其主要参数有：功率P=5 kW,直径D=7 m,转速N=107 r/min，叶尖速比λ=7，V=8 m/s，叶片个数B=3，功率系数CP=0.45，传动效率η=0.9，设计攻角α=70，升力系数CL=1.178 1,阻力系数CD=0.011 53。

将叶片半径沿展向平均分成20份，共21个截面，对文中前述的各个参数进行编程迭代计算，首先估算出a、b的初值，可应用下面的经验公式：

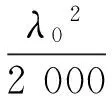
(28)

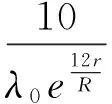
(29)

对修正的动量-叶素定理应用Matlab软件进行编程迭代计算[11-12]，流程图如图1所示。

图1 设计计算流程图Fig.1 Flow chart of design and calculation

由计算结果可以看出，弦长和扭角沿展长方向不断减少，进一步分析数据，发现靠近叶根处弦长和扭角过大，其他展长方向的弦长和扭角不能形成一定的连贯性。对此问题，需要对计算数据重新进行处理，考虑到叶片的叶尖损失，取0.2R～0.9R处的弦长和扭角进行拟合，由拟合公式计算出新的弦长和扭角值，修正后的动量-叶素理论计算的参数值和拟合后的参数值如表1所示，对经典理论计算的参数，由于篇幅限制，本文不再给出。对弦长和扭角计算值和拟合值进行比较，如图2、图3所示。

表1 各参数计算值及修正值Table 1 The calculated and corrected values of each parameter

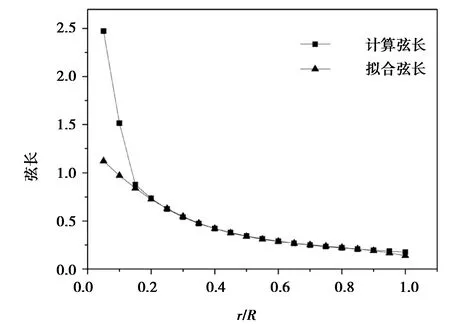
图2 弦长随r/R的变化Fig.2 Chord length along with r/R changes

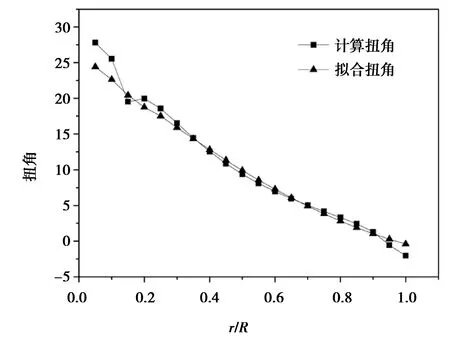
图3 扭角随r/R的变化Fig.3 Torsion angle along with r/R changes

从图2和图3可见，对于弦长，展向方向0.2R～0.9R拟合值与计算值非常吻合；对于扭角，展向方向0.3R～0.7R的拟合值与计算值有着很小的变化，弦长和扭角的差异主要在靠近叶根部分，拟合后的弦长和扭角曲线图都比未处理的曲线光滑。

对动量-叶素理论和修正的动量-叶素理论计算的轴向诱导因子、切向诱导因子和扭角进行比较，如图4、图5和图6所示。

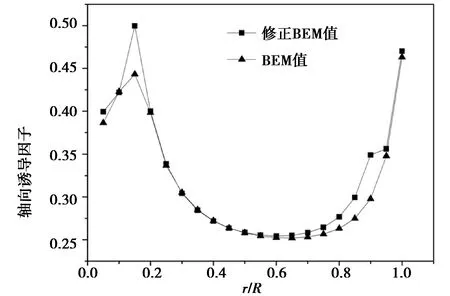
图4 动量-叶素理论与修正的动量-叶素理论计算的a值比较Fig.4 BEM comparison value of a value with modified BEM

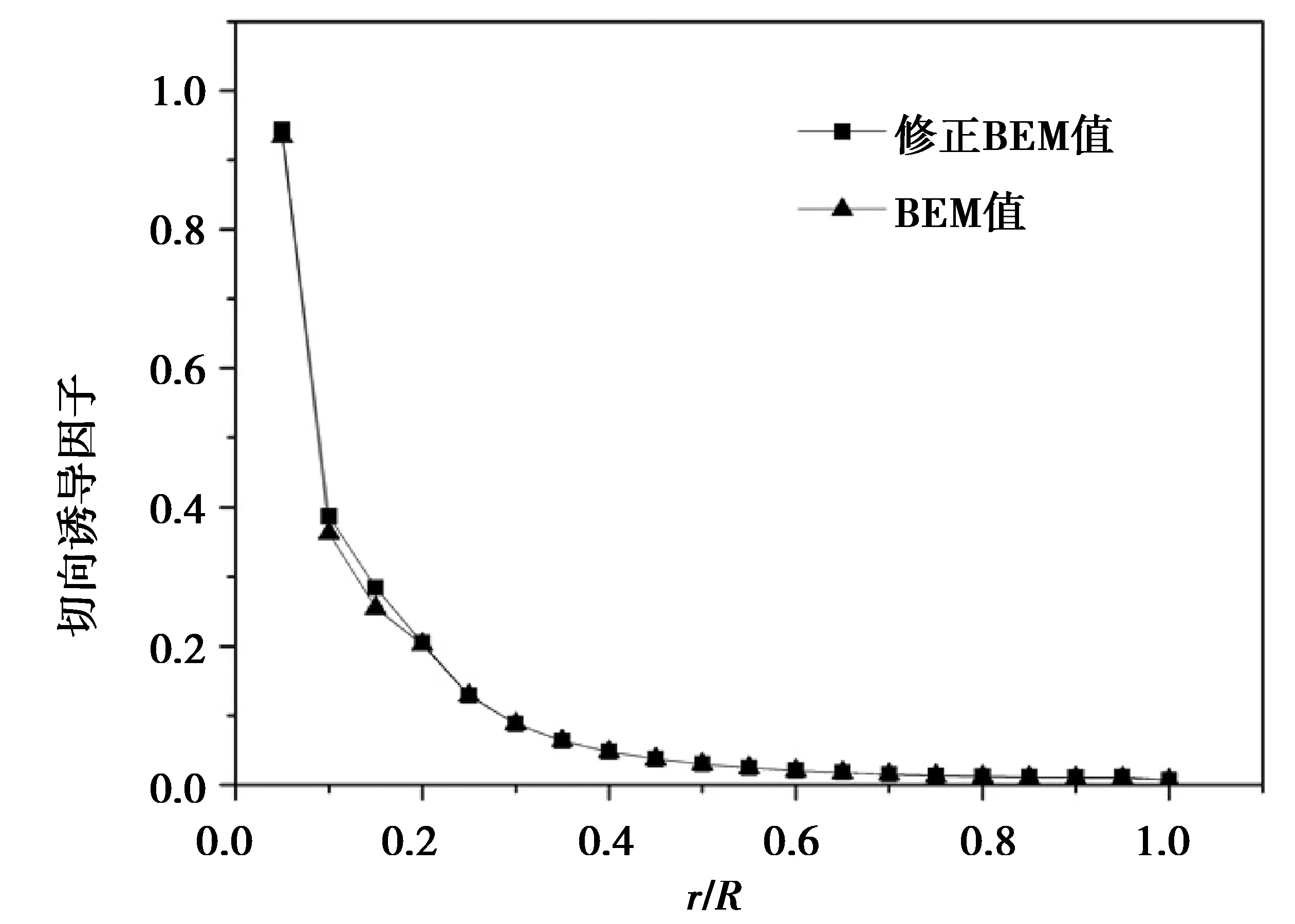
图5 动量-叶素理论与修正的动量-叶素理论计算的b值比较Fig.5 BEM comparison of b valuewith modified BEM

图6 动量-叶素理论与修正的动量-叶素理论计算的扭角值比较Fig.6 BEM comparison of torsion angle with modified BEM

从图4可以看出，修正后的动量-叶素理论对轴向诱导因子的影响主要在靠近叶根和叶尖部分，且修正后的轴向诱导因子参数值比未修正的大，主要原因在于尾流出现了分离，经典的动量理论已经不能再用了，导致修正后的轴向诱导因子增大；图5显示修正后的动量-叶素理论对切向诱导因子的影响主要在靠近叶根0.1R～0.2R处，其他部分和理想情况下的切向诱导因子比较吻合；由图6可以看出，修正理论相对于经典动量-叶素理论理论，靠近叶根0.05R～0.3R和叶尖0.8R～R处的扭角明显减少，且修正后参数的曲线更加光滑。

3 结 论

通过XFOIL软件和Matlab编程语言，应用动量-叶素定理和修正后的动量-叶素定理对某型号风力机叶片各个结构参数进行了计算，对计算出来的弦长和扭角进行线性拟合，对比了经典动量-叶素理论和修正的动量-叶素理论计算的扭角、轴向诱导因子和切向诱导因子以及拟合前后扭角和弦长，主要得出以下结论：

(1) 拟合前后的弦长和扭角差异主要在靠近叶根部分，拟合后的弦长和扭角曲线图都比未处理的曲线光滑；

(2) 修正的动量-叶素理论相对于经典动量-叶素理论计算的轴向诱导因子，主要区别在于叶根和叶尖部分，这是由于失速引起的，但是对于切向诱导因子的影响却非常小，对于扭角，主要修正靠叶根0.05R～0.3R和叶尖0.8R～R。

[1] 徐超,张兆德,于晓龙.1.5 MW风力机叶片设计与气动性能分析[J].浙江海洋学院学报,2015,34(2):35-39

XU C,ZHANG Z D,YU X L.Design and Aerodynamic Perilerformance Analysis of 1.5 MW vind Turbine Blade[J].Journal of Zhejiang Ocean University,2015,34(2):35-39

[2] 张明辉,宋丹丹,王海.基于改进遗传算法的风机叶片结构优化设计[J].煤矿设计,2015,36(10):56-60

ZHANG M H,SONG D D,WANG H.Structural Optinlization of Wind Turbine Blade Based on Improved Genetic Algoriuun[J].Coal Mine Machinery,2015,36(10):56-60

[3] 杨俊,武美萍,叶建友,等.风力机叶片气动设计与结构研究[J].机械制造,2014,52(12):24-28

YANG J,WU M P,YE J Y,et al.Research on Aerodynamic Design and Structure of Wind Turbine Blade[J].Machinery Manufacturing,2014,52(12):24-28

[4] PRANDTL L,TIETJENS O G.Applied Hydro and Aerom-echanics[M].Dover Publications,1957

[5] ROBERT E W,LISSAMAN P B S,WALKER S N.Aerody-namic Perfomance of Wind Turbines[M].Department of Mechanical Engineering ,Oregon State University,1976

[6] 刘雄,陈严,叶枝全.水平轴风力机气动性能计算模型[J].太阳能学报,2005,6(26):793-799

LIU X,CHEN Y,YE Z Q.Research on the Aerodynamic Performance Prediction Model for Horizontal Axis Wind Turbine[J].Acta Energiae Solaris Sinica,2005,6(26): 793-799

[7] 赵丹平,徐宝清.风力机设计理论及方法[M].北京:北京大学出版社,2012

ZHAO D P,XU B Q.Wind Turbine Design Theory and Method[M].Beijing: Peking University Press,2012

[8] 沈昕.水平轴风力机气动性能预测及优化设计[D].上海:上海交通大学,2014

SHEN X.Aerodynamic Performance Prediction and Optimization Design of Horizontal Axis Wind Turbines[D].Shanghai: Shanghai Jiaotong University,2014

[9] 陈进,王旭东,沈文忠,等.风力机叶片的形状优化设计[J].机械工程学报,2010,2(46):131-134

CHEN J,WANG X D,SHEN W Z,et al.Optimization Design of Blade Shapes for Wind Turbines[J].Journal of Mechanical Engineering,2010,2(46):131-134

[10] JAMIESON P.Innovation in Wind Turbine Design[M].London:John Wiley & Sons,Lt,2011

[11] 张峥,杨文平.MATLAB程序设计与实例应用[M].北京:中国铁道出版社,2003

ZHANG Z,YANG W P.Application of MATLAB Program Design and Example[M].Beijing: China Railway Press,2003

[12] 敖文刚,敖文芳.运用MATLAB对运动学、动力学问题进行过程分析[J].重庆工商大学学报(自然科学版),2012,29(6):36-40

AO W G,AO W F.Application of MATLAB to the Process Analysis of Kinematics and Dynamics[J].Journal of Chongqing Technology and Bussiness University(Natural Science Edition),2012,29(6):36-40

Research on Wind Turbine Blade Design Method

XUKai,WUDong-yin

(School of Energy and Power Engineering，Xi’an Jiaotong University，Shaanxi，Xi’an 710049，China)

In this paper,two theories of wind turbine blade design methods of classica blade element momentum theory and the corrected blade element momentum are compared,the parameters of the corrected blade element momentum theory are fitted ，In an example of a type of wind turbine,using matlab programming function,the specialized software xfoil of wind wing was used.The results show that the differences of chord length and twist angle before and after are mainly near the root of leaf; the main difference of the axial induction factor between classical blade element momentum theory and corrected blade element momentum theory is that the blade root and the tip portion,the effect of the tangential induction factor is very small.

blade element momentum theory；blade design；Matlab

TK89

：A

：1672-058X(2017)05-0082-06

责任编辑：罗姗姗

10.16055/j.issn.1672-058X.2017.0005.014

2017-03-11；

：2017-04-18.

国家重点研发计划重点专项项目(2016YFB0601403).

徐凯(1991-),男,陕西周至人,硕士研究生,从事风力机叶片设计研究．

**通讯作者：吴东垠(1966-)，男，内蒙古赤峰人，教授,博士，从事风力机叶片设计研究.E-mail:dongyinwu@xjtu.edu.cn．