风力发电系统雷击模型建立与仿真分析

付学文，魏智娟，庞先海，武桂桐，刘梁建，孟牧川

(1.国网河北省电力公司邢台供电分公司，河北 邢台 054001；2.国网河北省电力公司电力科学研究院，石家庄 050021)

风力发电系统雷击模型建立与仿真分析

付学文1，魏智娟1，庞先海2，武桂桐1，刘梁建1，孟牧川1

(1.国网河北省电力公司邢台供电分公司，河北 邢台 054001；2.国网河北省电力公司电力科学研究院，石家庄 050021)

将风力发电系统遭受雷击过电压的整个过程划分为风力发电机组、雷电流、接地系统分别进行研究，介绍搭建的风力发电系统的雷击数学模型，并利用专业计算软件进行仿真计算，总结风力发电系统雷击过电压规律，为风力发电系统防雷设计提供理论依据。

风力发电系统；雷击数学模型；雷击电流，接地系统

风力发电系统遭受雷击过电压整个过程直接建立数学模型比较复杂，无从下手。以下把风力发电系统遭受雷击过电压划分为3个子系统：雷电流、风力发电机组及接地系统，对其分别建立数学模型后在进行整合研究。利用ATP-EMTP等软件进行仿真计算，总结风力发电系统雷击过电压的一些共性规律。

1 风力发电机组的塔体电路模型

风电机组的塔体一般为空心圆台形钢质金属结构。风电机组所有的信号线、通信线以及电力传输线均被固定在塔体内侧，并被引到地面上的数据处理设备或接地系统上。为了更好地建立模型，可以将风电机组的塔体等效为圆柱体，如图1所示。

假设风叶可以将全部雷电流引入风电机组的塔体，认为雷电直接击中塔体。雷电流的起始频率非常的高，雷电流沿塔体的这种波过程可以近似为一个暂态过程。因此，可以将塔体用网格进行等段划分，划分后的每一段塔体可近似等效为Π形耦合电路[1-3]，如图2所示。网格的划分对于该模型的仿真计算结果非常重要，影响着计算的误差和计算时间。因此，在实际计算中进行网格划分时，采用试分的方法，逐渐加大分段数，直至相邻2次计算结果基本一致[4-6]。

图1 塔体的等效圆柱模型

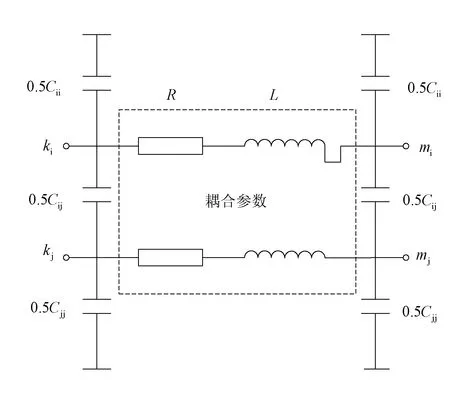
图2 分段塔体的等值电路

各分段塔体的自电容与分段塔体之间的互电容是由分段塔体电位系数矩阵得到的。导体电位系数矩阵采用文献[7]的平均电位法进行计算。在计算分段塔体电位系数时可以不计频率的影响，按照静电场理论来确定[8]。由于分段塔体间的静电场作用，各自之间半径相对它们之间的距离来说很小，所以可以将导体间的相互作用近似假设在各自的轴线上,见图3。

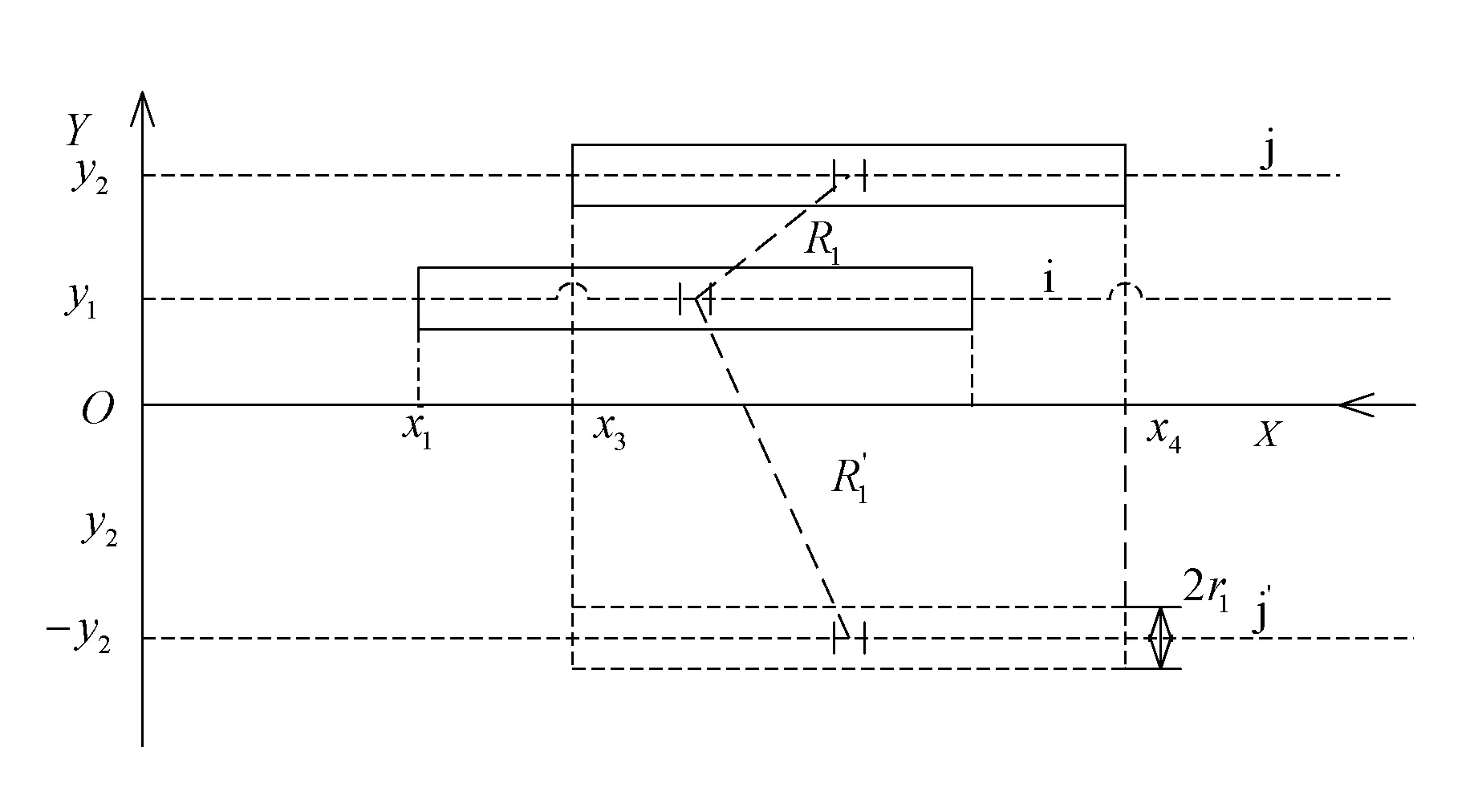
图3 两平行导体间的电容计算

对于如图3所示的塔体上2段相互平行导体i和j(i和j的半径为r1)，根据平行电位法，由导体j及其镜像j′在导体i上产生的平均电位分别如式(1)和式(2)所示。

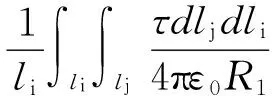
(1)

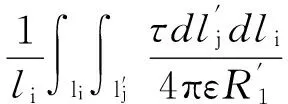
(2)

因此，导体i和导体j之间互电位系数为：

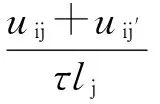
(3)

同理可得，由导体i及其镜像i′在导体j上产生的平均电位及电位系数。

分段塔体间的阻抗参数可按Neumann公式[9]来计算。在实际工程中，具有集肤效应的大地并非理想导体，因此，导体k和导体m与各自的镜像导体不在对称于地面。在均匀土壤中，导体k和导体m对称于土壤表层下某一复数深度的平面，该复数深度等于土壤的渗透深度[10]。

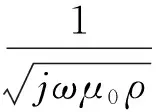
(4)

式中：ω为角频率；ρ为土壤电阻率，μ0为空气磁导率。

对于非均匀的土壤电阻，文献[10]也给出了相应的计算公式。对于地面上高度为h的水平分段塔体k与其自身的镜像体k′之间的距离为2h+2dp，所以水平分段塔体k和水平分段塔体m之间的互感可由水平分段塔体k及其自身的镜像体k′与水平分段塔体m之间的共同作用得到。

根据Neumann公式，任意水平分段塔体k和水平分段塔体m之间的阻抗可表示为

(5)

式中：dlm和dlk分别为水平分段塔体m和水平分段塔体k上的微分元，其方向向量和各自导体的参考方向一致，k′为k的镜像；D为2个微分元之间的距离；θ为两者之间的夹角。对于图4所示的两异面的导体，根据式(5)可计算它们之间的互阻抗为

Zkm=Z(dr)-Z(di)

(6)

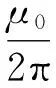
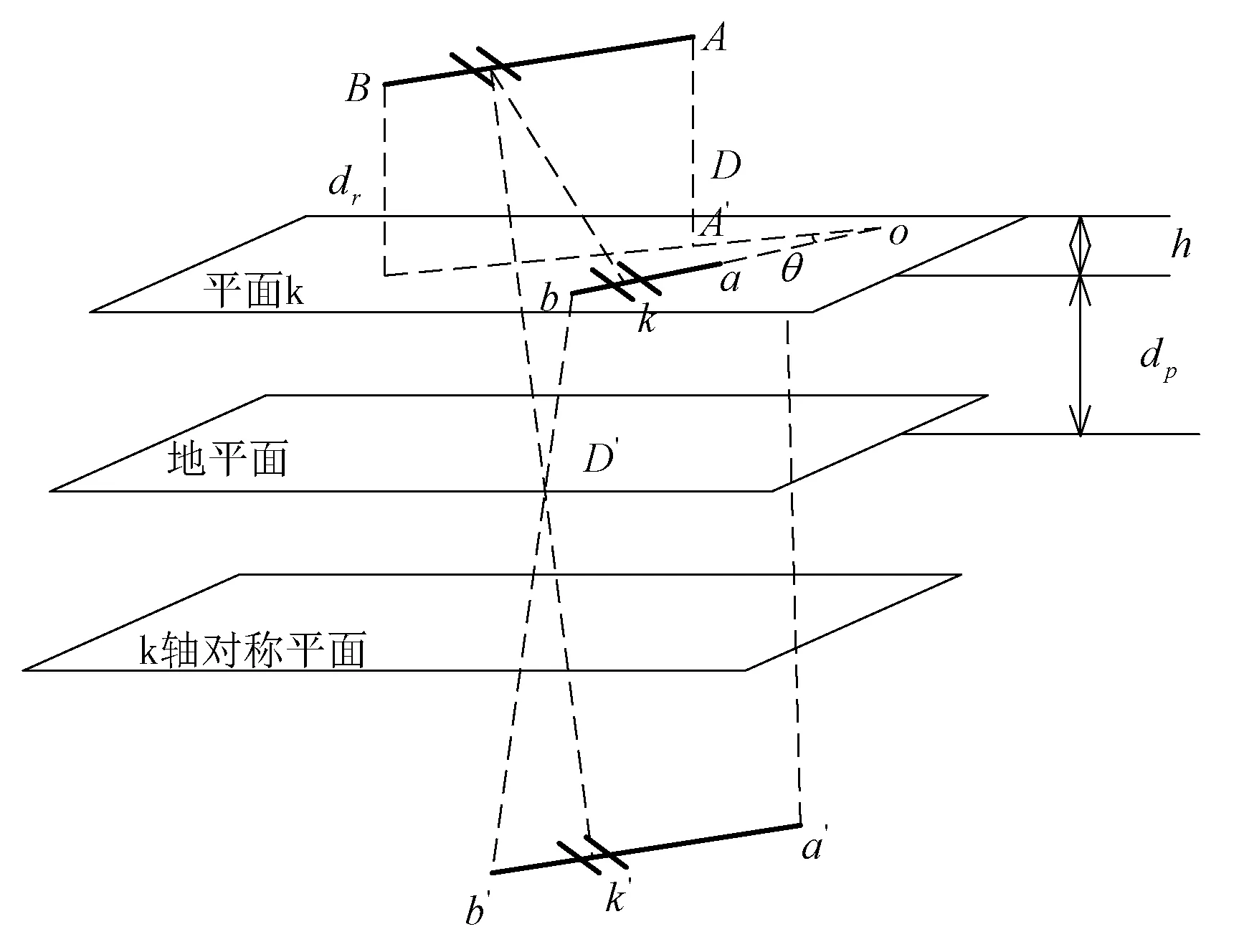
图4 两异面导体间的阻抗计算

2 风力发电系统的雷电流模型

雷电流模型采用双指数函数表达[11]

IL(t)=AIIm(e-αt-eβt)

(7)

式中：Im为雷电流的幅值，kA；AI、α、β为拟合常数，由常用波形公式[12]数据拟合得到。

2.1 10/350 μs波形

10/350 μs雷电流波形为回击的短脉冲雷电流，主要用于对地面设施的直接雷击防护设计，如GB 50057-1994《建筑物防雷设计规范》就规定采用此波形进行建筑物防雷设计，它也用于一些雷电电涌保护器的试验检测，其经验表达式为:

i=1.025Im(e-2.05×10-3t-e-0.564t)

(8)

式中：t为时间，μs。

2.2 0.25/100 μs波形

0.25/100 μs雷电流波形为后续回击的短脉冲雷电流，具有非常陡的波头上升沿，它在涉及雷电流变化率(波头陡度)的防护设计场合，如雷电电磁脉冲防护设计，就显得颇为重要。其经验表达式为：

i=1.002Im(e-7×10-3t-e34t)

(9)

2.3 8/20μs波形

8/20 μs雷电流波形是用于防雷保护装置试验的一种冲击电流波形，广泛用于各种雷电流电涌保护器的性能测试。其经验表达式为：

(10)

2.4 2.6/50μs波形

2.6/50 μs雷电流波形是我国电力行业规定采用的雷电流波形，广泛应用于输电线路和发、变电站的防雷设计，其经验表达式为：

i=1.058Im(e-1.5×10-2t-e1.86t)

(11)

3 风力发电系统的接地系统模型

风力发电机组的地网结构如图5(a)所示，为反映雷电流沿接地体传播的流动过程，将每一根导体按塔体网格划分的原则进行划分，划分后的每一小段导体分别等效为5(b)所示的π型电路。单位长度的电路参数[13]如式(12)-(15)所示。

(a) 接地网结构 (b) 接地分支导体等效电路

(12)

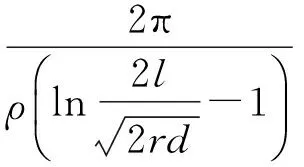
(13)

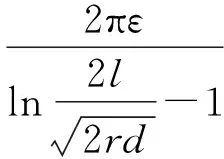
(14)

(15)

式中:ρe和ρ分别为接地体和土壤的电阻率；ε为土壤埋深的介电常数；l和r分别为接地体的长度与半径；d为接地体的在土壤中的埋深。

4 风力发电系统仿真实例

以内蒙古地区某风电场为例进行仿真，对实际数据进行等效处理。塔体的相对磁导率μr取60，电阻率ρ=0.139 Ω·mm2/m。该风电场的风力发电机组型号为M1500-600/150，其塔体高度为46 m，平均外径2.32 m，圆环形截面内外半径之比约为0.98，此时c≈0.99。 雷电流峰值取30 kA。建立风力发电系统ATP-EMTP仿真模型见图6。

图6 有电缆屏蔽层的风力发电系统ATP-EMTP模型

图6中，C0i为塔体的对地分布电容(i=1，2，……，10)，pF；Z1为每段塔体的阻抗,Ω+jμH；Z2为每段传输线屏蔽层的阻抗，Ω+jμH；Z3为每段传输线的阻抗，Ω+jμH；C12为每段塔体与传输线屏蔽层的分布电容，pF；C23为每段传输线屏蔽层与芯线的分布电容，pF；Rin为数据处理设备的输入电阻，取1 MΩ。

当3种雷电流分别作用在塔体顶端时，V1、V3、V5的电位仿真结果如图7-9所示。其中，V0代表10/350 μs、30 kA雷电流波作用在塔体顶端；V1代表0.25/100 μs、30 kA 雷电流波作用在塔体顶端；V2代表2.6/50 μs、30 kA雷电流波作用在塔体顶端。

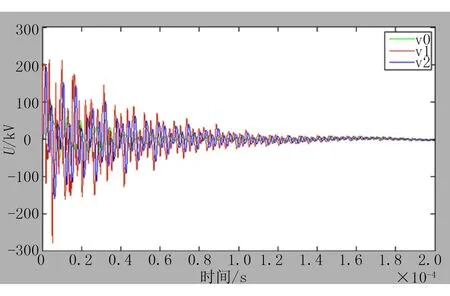
图7 V1的电位

5 结论

对系统仿真结果进行分析，可以找到一些共性的规律：

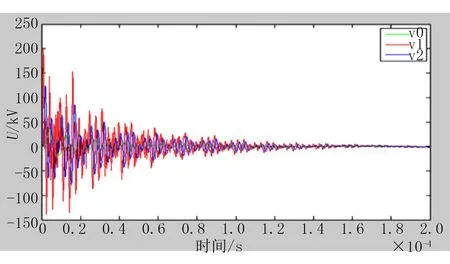
图8 V3的电位

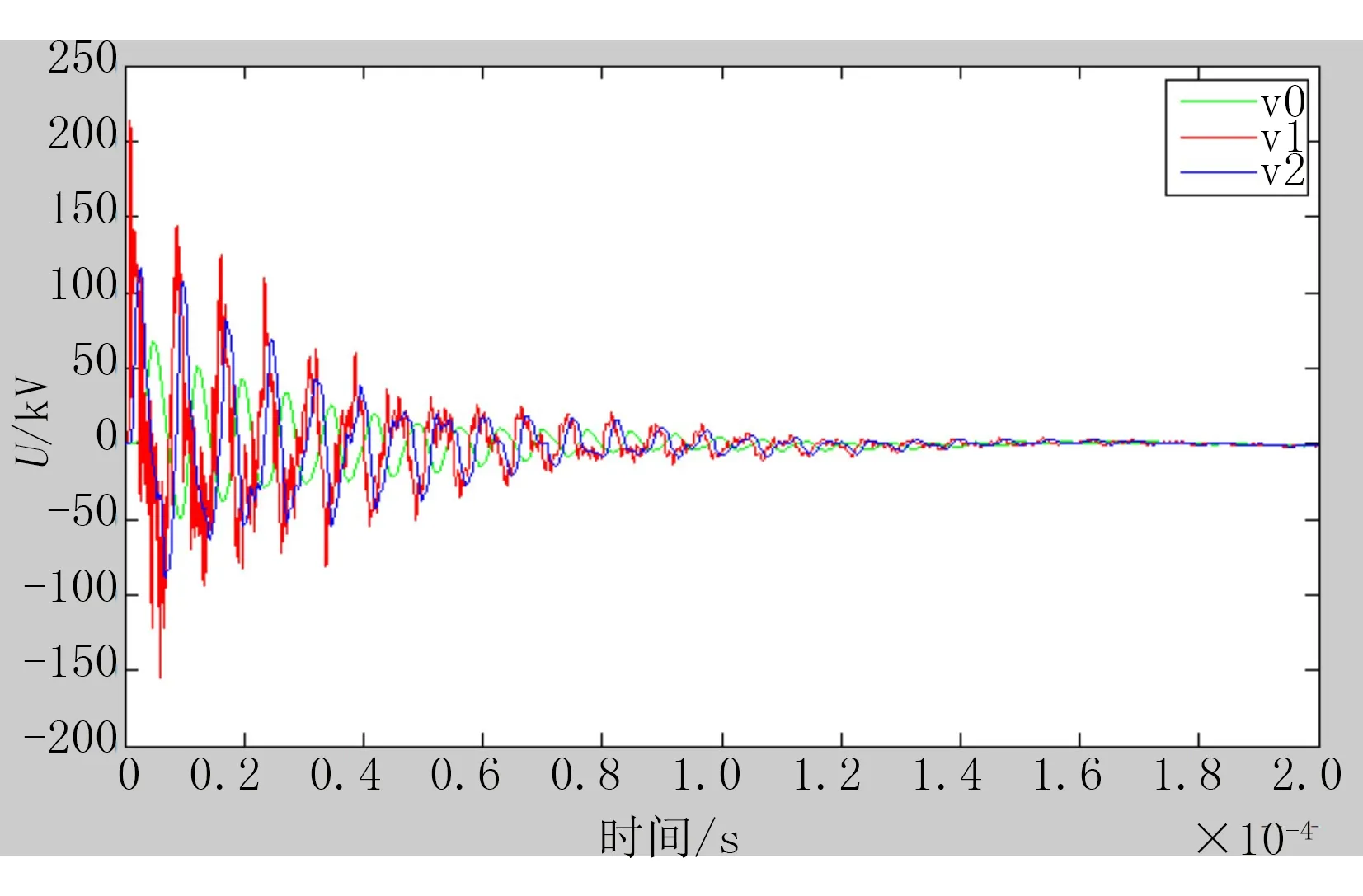
图9 V5的电位

a. 不同的雷电流波形作用时，塔体上同一点的电位是不同的,雷电流波形引起的过电压幅度：“0.25/100 μs、30 kA”>“2.6/50 μs、30 kA”>“10/350 μs、30 kA”；

b. 同一种雷电流波形作用时，无论是正向最大过电压幅值还是负向最大过电压幅值，所得到的过电压规律为塔体各段的雷击过电压与塔体各段所在位置的高度成正比；

c. 仿真实例所采用的3种雷电流波形作用时，在前18内各点都可以达到的自己正向最大过电压幅值与负向最大过电压幅值，多数在10以内达到自己正向最大过电压幅值与负向最大过电压幅值，在各点的雷电暂态过程的稳定时间是相同的，约在2.0以后就可以达到稳定状态。

[1] Buccella C, Feliziani M. A hybrid model to compute the effects of a direct lightning stroke on three-dimensional structures [J]. IEEE Transactions on Magnetics, 2003, 39(3): 1586-1589.

[2] Buccella C. An accurate numerical method to compute the effects of the protections against direct lightning on charged liquid tanks[C]∥Proceedings of IEEE 37th IAS Annual Meeting. Pittsburgh, PA, USA: IEEE, 2002: 1006-1011.

[3] Buccella C, Orlandi A. An efficient technique for the evaluation of lightning-induced voltage in a cylindrical vessel containing charged oil [J]. IEEE Transactions on Industry Applications, 2003, 39(2): 368-373.

[4] 赵海翔,王晓蓉.风电机组的雷击过电压分析[J].电网技术，2004,28(4) :27-29.

[5] 张小青.高层建筑钢筋结构体雷电暂态计算模型[J].中国电机工程学报,1996,16(5):306-310.

[6] 王晓辉,张小青.考虑参数频变特性的风机塔体雷电暂态计算[J].高电压技术,2009,35(6):1344-1349.

[7] Tosseli U J, Kochanov E S, Strunski M G. Calculation of electrical capacitances[M].Moscow, Russian: Energy Press,1981.

[8] 吴维韩,张芳榴. 电力系统过电压数值计算[M].北京:科学出版社,1989.

[9] Grover F W. Inductance calculations [M].New York,USA:Dover Press,1998.

[10] Deri A, Tevan G, Semlyen A, et al, The complex ground return plane: a simplified model for homogeneous and multi-layer carth return[J]. IEEE Transaction on Power apparatus Systems,1981,100(8):3686-3693.

[11] Aguado M, Hermoso B, etc. Risks assessment for lightnings strokes in wind farm installation [C].High Voltage Engineering, Eleventh International Symposium on (Conf. Publ. No. 467).IEEE,1999,(2)：357-360.

[12] Peter Hasse.Overvoltage protection of low voltage systems [M].傅正财,叶蜚誉译.2版.北京:中国电力出版社,2005.

[13] Velazquez R, Mukheddkar D. Analytical modeling of grounding electrode transient behavior[J].IEEE Transactions on Power Apparantus Systems,1984,103(6):1314-1321.

本文责任编辑：王洪娟

Establish and Simulation Analysis on Lightning Strike Model of Wind Power System

Fu Xuewen1，Wei Zhijuan1Pang Xianhai2，Wu Guitong1，Liu Liangjian1,Meng Muchuan1

(1.State Grid Hebei Electric Power Corporation Xingtai Power Supply Branch，Xingtai 054001,China；2.State Grid Hebei Electric Power Research Institute，Shijiazhuang 050021,China)

This paper researches the whole process for wind power system of lightning overvoltage from the wind turbine generator system, lightning stroke current and the grounding system respectively,sets up a lightning strike mathematical model for the entire wind power system, summarizes the wind power system lightning overvoltage rules. This is the theoretical basis of lightning protection design for wind power system.

wind power system;lightning mathematical module;lightning stroke current;grounding system

TM863

：A

：1001-9898(2017)04-0001-04

2017-02-28

付学文(1983-)，男，工程师，主要从事电力系统过电压与绝缘配合相关工作。