一种利用低秩矩阵填充技术恢复气象数据的方法

臧 芳

(湖南大学信息科学与工程学院 湖南 长沙 410012) (湖南电子科技职业学院机械与电子信息工程分院 湖南 长沙 410205)

一种利用低秩矩阵填充技术恢复气象数据的方法

臧 芳

(湖南大学信息科学与工程学院 湖南 长沙 410012) (湖南电子科技职业学院机械与电子信息工程分院 湖南 长沙 410205)

矩阵填充技术是继研究压缩感知技术之后又一备受关注的新技术，并已被应用于科学与工程等诸多领域。矩阵填充技术主要研究如何通过已知的部分矩阵数据来达到恢复整个矩阵的目的。气象数据为天气预报和开展各种气象服务提供依据，具有空间相关性和时间稳定性，加上气象数据矩阵的低秩性，为研究如何利用低秩矩阵填充技术对气象数据的连续获取提供了条件。最后通过真实气象数据进行了仿真实验，证明了该方法的有效性。

低秩性 气象数据 矩阵填充 气象预测

0 引 言

压缩采样[1]理论一经提出，就引起信息论[2-5]、图像处理[6-9]、无线通信、大气等领域的广泛关注。其中，矩阵填充[10-22]是压缩采样领域的重要理论，主要作用是能利用已知矩阵的部分数据来恢复缺失数据。

气象数据采集技术的发展与更新为当前气象数据的采集、处理、预测提供了强有力的支持。气象数据的采集通过无线传感器完成，涉及地区广，问题规模大。整个采集过程受采集器的精确度、存储容量、处理速度、能耗等方面的影响。同时气象数据又有时间与空间的相关性优势，即地理位置相邻的同一时段区域其天气往往相差不多。因此，采集完整的气象数据既不经济也不现实。如果气象数据所对应的矩阵低秩合理，那么气象数据的完整性可以用矩阵的恢复技术来实现。

文中主要针对气象数据的完整性研究提出了利用矩阵填充技术来实现的方法。最后采用了真实气象数据进行实验验证，结果证明：文中提出的矩阵填充算法能较好地恢复气象数据，并能有效解决传感器存储容量过大、能耗过大等问题。

1 相关研究

工作实际中碰到的矩阵大多具有低秩性或类似低秩性，而低秩性是该矩阵具有唯一解的必备条件[12]。某一缺失元素的矩阵，如果能在原有数据的基础上根据矩阵的低秩结构来补全矩阵元素，称此过程为矩阵恢复。

矩阵填充理论研究侧重研究矩阵的可填充性。而仅当研究矩阵元素数量大于一定数才有可填充性。Candès等研究者[12,28]用大量实例证明了当采样矩阵的奇异值及已知矩阵元素数量达到一定的标准时，绝大多数低秩阵可求凸优化问题而完好地还原矩阵。但经验证该方法并不十分可行。

近年来，国内外许多学者针对该问题设计出了精确低秩矩阵填充重构算法[23-27]，取得了一系列可喜的成果。涉及精确低秩矩阵填充的重构算法除了奇异值阈值SVT(Singular Value Thresholding)算法[29-31]，还有SET算法[13]和OptSpace 算法[22]。

1.1 SVT算法

Cai[14]等提出了一种简单的适用于较大规模矩阵填充的方法：SVT算法。利用SVT算法解矩阵恢复问题，可描述为：

min‖X‖*subject toPΩ(X)=PΩ(M)

算法1矩阵填充的SVT算法

1:初始化Y0=0，

2：while not converged do

3: Xk=Dτ(Yk-1),

4: Yk=Yk-1+δkPΩ(M-Xk).

5: end while

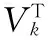
1.2 SET算法

SET(Subspace Evolution And Transfer)算法[13]是由Dai等提出的一种新算法。SET算法在已知秩的情况下采用查找列空间来匹配矩阵。主要有子空间演化(使用线性查找程序细化列空间)和子空间转换构成。SET算法针对此问题在子空间转换部分，设置用于检测障碍的机制，并将列空间转换位置。实践证明，该算法对超低秩矩阵非常有效，缺点是收敛慢，在若干的迭代次数后，因检测机制远离列空间而易失效。

1.3 OptSpace 算法

针对矩阵恢复问题，Keshavan等提出了OptSpace算法[22]。其主要使用谱方法在格拉斯曼流形[32-33]上进行目标函数优化，可从随机观测中恢复低秩矩阵的算法。重点对目标矩阵进行尽可能恢复，在对修复后的矩阵进行投影时借助缩放因子来补充矩阵中检测到的项数相对于原始矩阵而言的较小均值，最后运用格拉斯曼流形空间上的梯度下降法来求解获得最小目标函数，即获得矩阵恢复最小误差值。文献[34]给出了该算法可行的理论支撑。与原始矩阵填充区别在于：必须事先获得秩。

与SET算法有着相同之处：两者均作用于格拉斯曼流形上，且通过流形上的线性查询得到目标值。不同之处在于：SET算法要求秩必须已知，利用列空间来获得目标矩阵；而OptSpace算法行空间和列空间均需查找，增大了数据修复的难度，而且线性搜索不可确保收敛性，也是由于搜索路径影响该算法得到最佳答案。

2 气象数据特征分析

为证明气象数据恢复能利用矩阵填充技术进行研究，首先对气象数据的特性进行详细分析。

2.1 平稳性

由实际气象数据分析可知，同一站点在较短时间内气象变化一般波动不大。在此，利用相邻时间段的气象数据差值分布来探究气象数据在一段时间内的相对平稳性。用s表示气象观测站点号，t表示某个时间点，则相邻间隔差值函数可表示为：

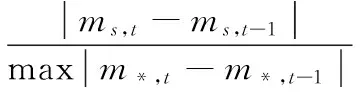
(1)

由于气象数据量庞大，实验只选取每年各季节的一段数据集。图1描述了春夏秋冬各季度气象数据相邻间隔差值分布，横轴表示归一化的差值大小，纵轴表示累计分布百分比。从下面四个组图中得知，接近1的相邻间隔差值都保持在0.1之内，证明了相邻时间段的气象数据数值有较好的时间平稳性。

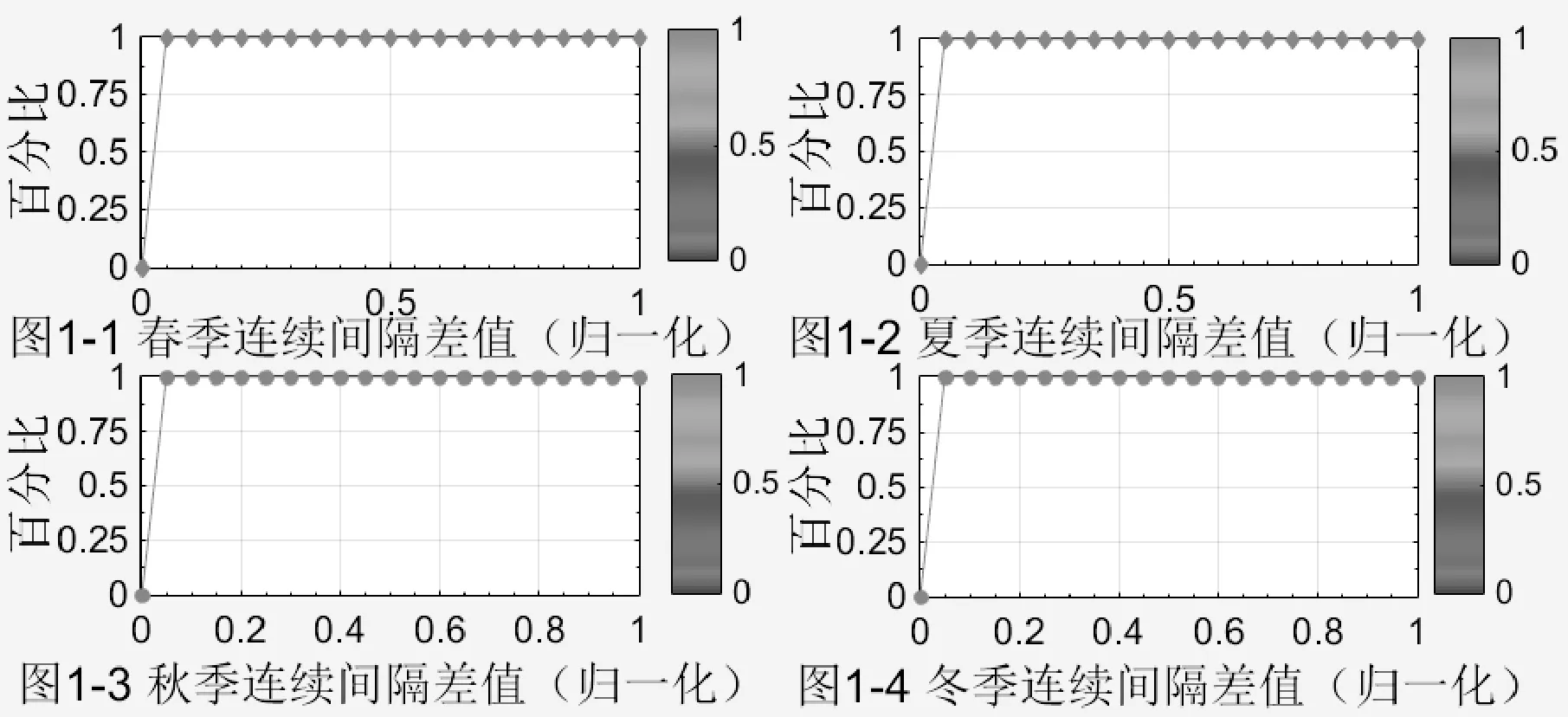
图1 春夏秋冬气象数据的相邻间隔差值分析图

2.2 低秩性

相邻地区如株洲与长沙，经常能同时有晴天或同时下雨。这说明气象数据除了具有时间上的平稳性，还具有空间上的相关性。为此，假设气象数据构成的矩阵具有低秩性，如果能证明其具有低秩性这证明气象数据的恢复适合用低秩矩阵填充技术实现。以下通过分析真实气象数据矩阵的最大L个奇异值累计贡献率来验证其低秩性。

矩阵A∈Cm×n的奇异值分解成A=U∑VT。σi为矩阵A的奇异值，n为奇异值总个数，最大L个奇异值累积贡献率：

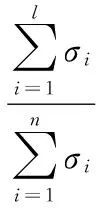
(2)

由于数据集较大，实验分别选取一年四季数据中各自一段数据集进行验证。图2描述了12天，288个测量时间点四季气象数据矩阵的最大L个奇异值累积贡献率。图2的四个组图说明最大的50个奇异值，基本蓄积了全部奇异值接近99%的能量。充分证明气象数据具有很好的低秩性，具有能利用矩阵填充技术的条件。

图2 四季气象数据最大L个奇异值累积贡献分布

3 问题的解决

3.1 数据采集

为了解决传感器能量消耗过大的问题，就不能在每个时间点采集所有站点的气象数据。气象数据的时间与空间相关性使采集的部分数据对剩余部分利用矩阵填充技术进行推断成为可能。Candes等提出伯努利模型[12]证明了矩阵元素可独立采样，但要求获取的元素要满足在矩阵的每一行和每一列都有分布。该实验利用伯努利模型对气象数据进行采集。假设气象数据的矩阵为A∈Cm×n，m表示站点数目，n为总测量时间点。对应站点对应时间点的气象数据测量值aij表示矩阵元素的大小。每一列数据表示某一时间点采集到全部站点的气象数据。通过[0,1]投影矩阵决定在该时刻是否采集。则相应的采样矩阵表示成：

Bm×n=P[A]Ω

(3)

采样描述如图3所示。

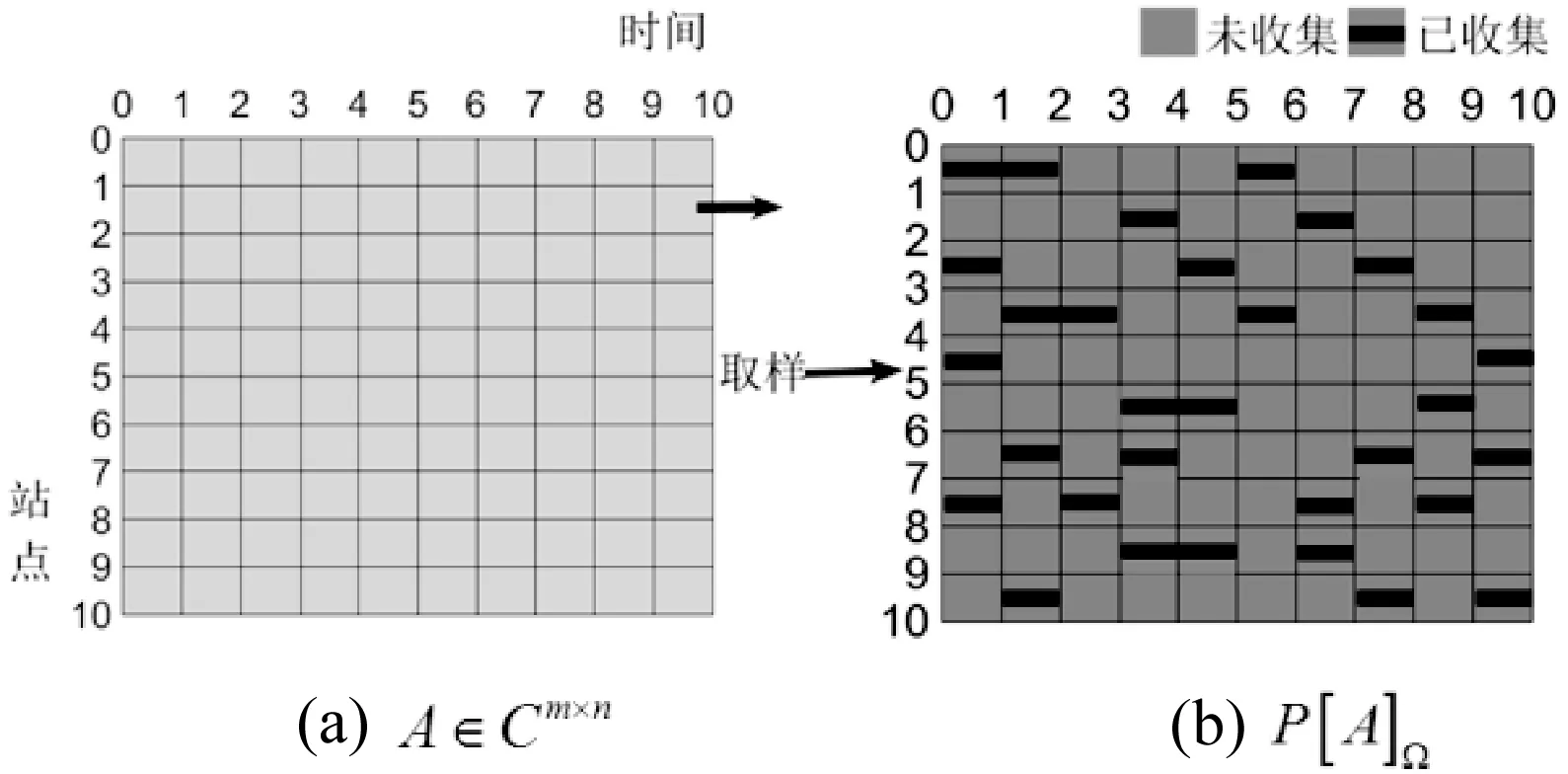
图3 气象数据的采集模型

3.2 数据预测

图3中纯深灰色区域为未采集气象数据，利用填充技术得到如图4(b)中深灰底白杠部分数据。

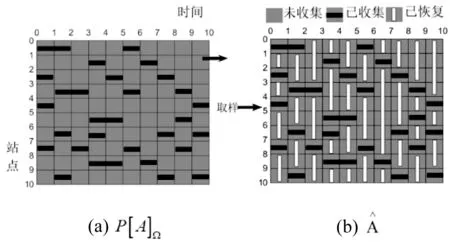
图4 气象数据的预测模型

计算数学基础文献[12]中指出：矩阵具有低秩性的情况下，根据矩阵恢复技术定义，可将矩阵恢复问题可转化为如下：

minimizerank(X)subject toXij=Aij(i,j)∈Ω

(4)

式中的Aij为采集到的值，Ω为采样矩阵元素下标的集合。由上述公式可以推断：矩阵填充问题就是在保证矩阵低秩性的良好结构的前提下进行数据补全。填充数据时秩(rank)用核范数来替代。核范数定义为：

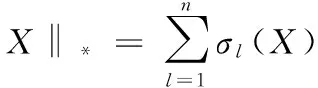
(5)

式中σl代表降序的第l个奇异值。由此，解决的优化问题由式(4)导出式(6)：

minimize ‖X‖*subject toXij=Aij(i,j)∈Ω

(6)

文献[12]中指出，对于满足不相关假设的秩为r并且大小为n1×n2的A低秩矩阵，测量矩阵和稀疏矩阵间不包含相关元素，当采样数目达到一定时就可精确还原。但这类优化问题无法处理大型矩阵，如气象数据。研究者针对此种凸优化问题给出了若干应对算法，如文中提到的SVT算法[25]、IALM算法[35-36]等、贪婪追踪方法和基于格里斯曼流形空间的方法等。

3.3 连续预测

本实验对于气象数据的连续获取，采用基于移动窗口形式来保持算法中被填充矩阵的大小不变来实现。首先对一段连续时间点均匀采集部分数据，获得初始窗口。然后利用矩阵填充对未采集的数据进行恢复，得到完整数据集。在得到前一阶段完整数据之后，同样只采集下一时刻的部分数据，保持矩阵窗口大小不变，向前移动一个时刻点，重新组成采样矩阵，然后利用矩阵填充恢复其他数据。如图5所示。

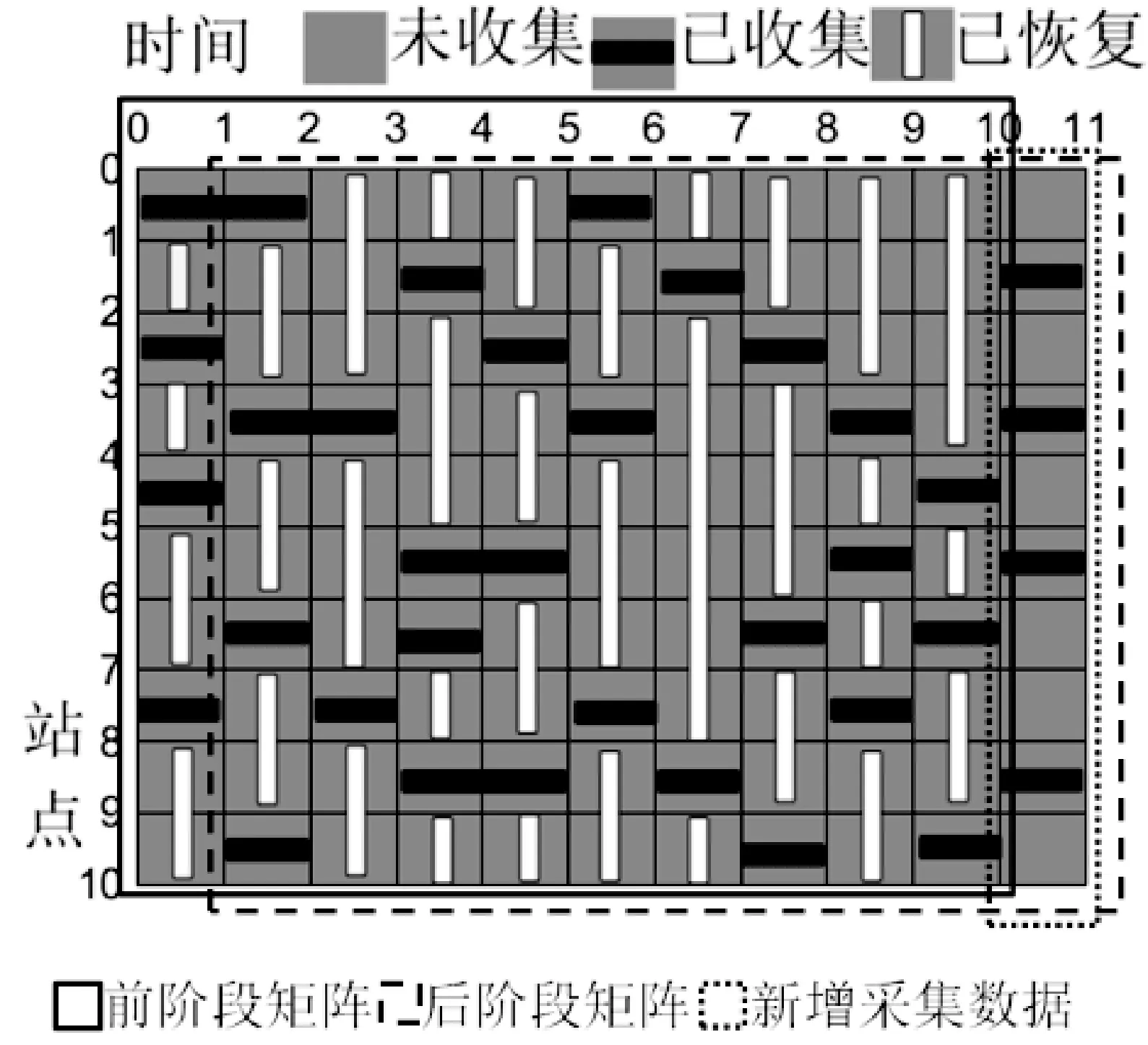
图5 气象数据连续预测窗口模型

图5中横向1～10表示首次采集时间段，2～11表示下一个采集时间段。该过程重要步骤为在矩阵右侧增添一列数据，然后去掉原有矩阵左侧首列数据。

4 连续获取数据算法

先确定初始窗口的大小，得到均匀采集部分数据后，应用矩阵填充技术获得全部数据。基于移动窗口形式保持运算矩阵大小不变，然后更新采样矩阵来获取后续的气象数据。描述如算法2。

算法2基于矩阵填充的气象数据获取

1.初始化：t=0，窗口列大小=n，采样比例=v。

2.应用均匀采样，选取n长的时间段，按照采样比例，对数据进行连续采样，获取采样矩阵A(t)。

3.矩阵填充算法应用于A(t)，获得恢复矩阵X(t)。

4.t=t+1，进入下一窗口，按照采样比例，对下一时刻的数据进行采样，获取新增一列的采样位置集合C，去掉前一窗口第一列，重新组成新的采样矩阵A(t)。

5.矩阵填充算法应用于A(t)，获得恢复矩阵X(t)。

6.未结束转到4，否则停止。

5 实 验

5.1 实验过程

本测试利用均方值误差计算法来衡量预测气象数据值与实际气象数据值之间的误差。如果误差越小，说明该算法精度越高。

实验数据采用2014年到2015年，每年中四个季度的气象降雨量数据，通过不同数据采样率(60%、50%)，对文中提到的SVT、SET、OptSpace三种算法进行性能权衡。通过柏努利模型对若干个站点均匀采集气象数据，柏努利采样模型，可以保证获取的元素满足在矩阵的每一行和每一列都存在分布，有助于矩阵填充算法对气象数据的重构。实验中还借助MATLAB软件进行构图，利用低秩矩阵填充算法求解。模型中设置n=24×12, 12代表12天的时间测量点。

5.2 实验结果

图6为采样率为50%连续预测恢复误差对比图，恢复误差都小于0.04，算法精度较高。图7描述了60%的数据连续预测恢复误差对比实验结果。与图6相比，图7随着采集数目增多，填充精度也有了较大的提高。因此可以推断：如果充分随机的采集一定量的气象数据，是完全能够填充其他气象数据的。柏努利采样模型，可以保证获取的元素满足在矩阵的每一行和每一列都存在分布，有助于矩阵填充算法对气象数据的重构。测试结果充分证明了利用低秩矩阵填充技术恢复气象数据的方法的实效性。

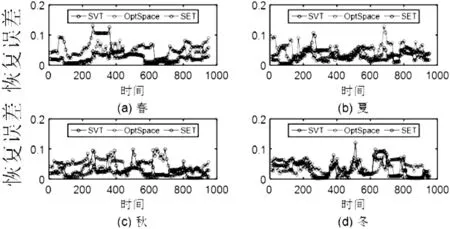
图6 采样率为50%的气象数据预测误差对比图

图7 采样率为60%的气象数据预测误差对比图

6 结 语

本文首先介绍了几种精确低秩矩阵填充的重构算法，如适合于较大规模矩阵恢复的SVT算法、使用谱方法在格拉斯曼流形上进行目标函数优化的OptSpace算法和采用寻找列空间来匹配采样矩阵，秩必须已知的SET算法。然后重点对几种矩阵填充方法用于低秩气象数据矩阵填充问题进行数据测试，最后选取不同参数实施矩阵重建，并验证了矩阵重建效果。

从以上实验得知：如果充分获取一定比例的随机气象数据，可通过柏努利采样模型恢复得到绝大部分其他气象数据。柏努利采样模型，可以保证获取的气数据在矩阵的每一行和每一列都有分布。根据气象数据具有的时间与空间的相关性，气象数据构成的矩阵还具有低秩特点，基于矩阵填充算法重构出气象数据矩阵。

文中提出的矩阵填充算法能较好地恢复气象数据，并能有效解决传感器存储容量过大、能耗过大等问题。该方法实用有效。

[1] Donoho D L.Compressed Sensing[J].Information Theory,Ieee Transactions on,2006,52(4):1289-1306.

[2] 叶蕾,郭海燕,杨震.基于压缩感知重构信号的说话人识别系统抗噪方法研究[J].信号处理,2010,26(3):321-326.

[3] 季云云,杨震.基于自相关观测的语音信号压缩感知[J].信号处理,2011,27(2):207-214.

[4] 孙林慧,杨震.基于压缩感知的分布式语音压缩与重构[J].信号处理,2010,26(6):824-829.

[5] 高畅,李海峰,马琳.面向内容的语音信号压缩感知研究[J].信号处理,2012,28(6):851-858.

[6] 朱明,高文,郭立强.压缩感知理论在图像处理领域的应用[J].中国光学,2011,4(5):441-447.

[7] 王芳.基于压缩感知的图像处理与重构方法[J].光电子·激光,2012(1):196-202.

[8] 焦铸.压缩感知在图像处理中的应用[D].西安理工大学,2011.

[9] 丁伟.基于压缩感知的水下图像处理[D].中国海洋大学,2013.

[10] Balzano L,Nowak R,Recht B.Online Identification and Tracking of Subspaces From Highly Incomplete Information[C]//Communication,Control,and Computing (allerton),2010 48th Annual Allerton Conference on,2010:704-711.

[11] Keshavan R H,Montanari A,Oh S.Matrix Completion From a Few Entries[J].Information Theory,Ieee Transactions on,2010,56(6):2980-2998.

[12] Candès E J,Recht B.Exact Matrix Completion via Convex Optimization[J].Foundations of Computational Mathematics,2009,9(6):717-772.

[13] Dai W,Milenkovic O.Set:an Algorithm for Consistent Matrix Completion[C]//Acoustics Speech and Signal Processing (icassp),2010 Ieee International Conference on,2010:3646-3649.

[14] Cai J,Candès E J,Shen Z.A Singular Value Thresholding Algorithm for Matrix Completion[J].Siam Journal on Optimization,2010,20(4):1956-1982.

[15] Candes E J,Plan Y.Matrix Completion with Noise[J].Proceedings of the Ieee,2010,98(6):925-936.

[16] Chen Y.Incoherence-optimal Matrix Completion[J].IEEE Transactions on Information Theory,2013,61(5):2909-2923.

[17] Geelen J F.Maximum Rank Matrix Completion[J].Linear Algebra and Its Applications,1999,288:211-217.

[18] Candès E J,Tao T.The Power of Convex Relaxation:Near-optimal Matrix Completion[J].Information Theory,Ieee Transactions on,2010,56(5):2053-2080.

[19] Ma S,Goldfarb D,Chen L.Fixed Point and Bregman Iterative Methods for Matrix Rank Minimization[J].Mathematical Programming,2011,128(1):321-353.

[20] Chen Y,Bhojanapalli S,Sanghavi S,et al.Coherent Matrix Completion[J].Proceedings of the 31st International Conference on Machine Learning,Beijing,China,2014:674-682.

[21] Recht B.A Simpler Approach to Matrix Completion[J].The Journal of Machine Learning Research,2011,12(4):3413-3430.

[22] Keshavan R,Montanari A,Oh S.Matrix Completion From Noisy Entries[C]//Advances in Neural Information Processing Systems,2009:952-960.

[23] 赵玉娟,郑宝玉,陈守宁.矩阵填充及其在信号处理中的应用[J].信号处理,2015(4):423-436.

[24] 张玮奇,张宏志,左旺孟,等.基于加权核范数最小化的矩阵填充模型[J].计算机科学,2015,42(7):254-257.

[25] 方茂中.关于矩阵填充和非负矩阵的研究[D].华东师范大学,2008.

[26] 韦仙.基于矩阵填充技术重构低秩密度矩阵[J].武汉工程大学学报,2015,37(2):72-76.

[27] 刘旭东,陈德人,王惠敏.一种改进的协同过滤推荐算法[J].武汉理工大学学报(信息与管理工程版),2010,32(4):550-553.

[28] Candès E J,Plan Y.Matrix Completion with Noise[J].Proceedings of the Ieee,2009,98(6):925-936.

[29] 陈峰峰.奇异值阈值算法在Netflix问题中的应用研究[D].清华大学,2011.

[30] 孟樊,杨晓梅,周成虎.遥感影像低秩信息的矩阵填充复原方法[J].测绘学报,2014,43(12):1245-1251.

[31] 王平.基于凸优化的矩阵重建问题算法的研究[D].海南师范大学,2014.

[32] Ngo T,Saad Y.Scaled Gradients on Grassmann Manifolds for Matrix Completion[C]//Advances in Neural Information Processing Systems,2012:1412-1420.

[33] Boumal N,Absil P A.Low-rank Matrix Completion Via Preconditioned Optimization on the Grassmann Manifold[J].Linear Algebra & Its Applications,2015,475:200-239.

[34] Wong R K W,Lee T C M.Matrix Completion with Noisy Entries and Outliers[D].University of California,2016.

[35] Lin Z,Chen M,Ma Y.The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-rank Matrices[J].Arxiv Preprint Arxiv:1009.5055,2010.

[36] Goldfarb D,Ma S,Scheinberg K.Fast Alternating Linearization Methods for Minimizing the Sum of Two Convex Functions[J].Mathematical Programming,2013,141(1):349-382.

METHODOFRESTORINGMETEOROLOGICALDATAUSINGLOW-RANKMATRIXFILLINGTECHNIQUE

Zang Fang

(CollegeofComputerScienceandElectronicEngineering,HunanUniversity,Changsha410012,Hunan,China) (InstituteofMechanicalandElectronicInformationEngineeringBranch,HunanVocationalCollegeofElectronicandTechnology,Changsha410205,Hunan,China)

Matrix filling is another attractive new research field after compressive sensing. It has been applied in the fields of science and engineering. Matrix filling principally studies how to restore the whole matrix elements by the known partial matrix elements. The meteorological data have the spatial correlation，time stability, and low rank of meteorological data matrix. All these advantages provide the continuous acquisition of meteorological data for researching how to use the low rank matrix filling technique. Finally, the simulation experiments are performed by real weather data, and the effectiveness of the method is proved.

Low-rank Meteorological data Matrix filling Meteorological forecast

TP391

A

10.3969/j.issn.1000-386x.2017.09.063

2016-11-11。臧芳，讲师，主研领域：软件工程。