基于卷积神经网络的信道均衡算法

陈敏华 李 杨 张武雄

(中国科学院上海微系统与信息技术研究所 上海 201210)

基于卷积神经网络的信道均衡算法

陈敏华 李 杨 张武雄

(中国科学院上海微系统与信息技术研究所 上海 201210)

在现代无线通信系统中，为了克服由传输信道的非线性以及多径效应引起的符号间干扰，解决传统信道均衡算法难以适应的时变信号均衡问题，提出一种基于卷积神经网络的信道均衡算法。通过采集实际通信系统中发送端的相位偏移调制QPSK(quadrature phase shift keying)发送符号序列及接收端的接收符号序列，并将其分割为训练集和测试集来训练及测试卷积神经网络均衡器。实验结果验证了在相同信噪比条件下，基于卷积神经网络的信道均衡算法对QPSK恢复的误符号率相比RLS算法和MLP算法分别降低了20%和5%。

信道均衡 卷积神经网络 无线通信 深度学习

0 引 言

信道均衡技术可以有效降低符号间干扰对通信系统的影响，对数字通信技术的发展起着关键作用。常用的信道均衡技术主要分为两类，一类是基于训练的信道均衡，包括最小均方滤波LMS(least mean square)[1]和迭代最小二乘法RLS(recursive least square)[2]等；另一类为盲均衡算法，主要有恒模算法CMA(constant modulus algorithm)[3]，多模算法MMA(multi-modulus algorithm)[4]等。传统的信道均衡技术往往将信道建模为一个线性系统，通过迭代算法不断逼近最优的线性模型来找到最优参数。但是非线性特性强烈及多径丰富的环境下，传统的信道均衡算法由于无法拟合非线性系统，因而并不能保证较低的误码率。

人工神经网络由于其拟合非线性系统的能力在信道均衡领域吸引了很多关注。文献[5-6]分别使用不同结构的神经网络进行信道均衡，并证明在相同信噪比条件下，神经网络算法能达到更低的误比特率。文献[7]提出了一种搜索优化的方法来训练神经网络，提升了网络的训练速度。文献[8-9]提出用神经网络解决5G通信和可见光通信等不同场景下的信道均衡问题的方法。但是由于受到无线数据采集能力的限制，这些工作都只在理论和计算机仿真角度验证了神经网络解决信道均衡问题的可行性，缺乏在实际数据集上的验证。

鉴于此，本文提出了一种基于卷积神经网络的信道均衡算法，并在实际采集的QPSK调制发送符号序列及接收符号序列组成的数据集上进行测试。

1 问题建模

1.1 信道均衡

本文将自适应信道均衡问题建模为一个可以用神经网络求解的多分类问题，并基于softmax回归分析[10]方法计算分类的条件概率。

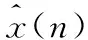
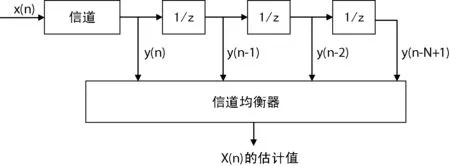
图1 信道均衡总体结构

1.2 softmax回归模型

传统的逻辑回归只能解决二分类问题，而 softmax回归模型是逻辑回归在多分类问题上的一种推广。假设采用softmax回归模型，对应每组特定的接收端信号Y(n)，均衡器输出的条件概率分布函数为：

(1)

式中ω=[ω1,ω2,…,ωk]为模型的参数。根据式(1)，可以得到总的概率分布函数为：

(2)

1.3 模型求解

求解模型的过程就是不断优化模型参数以降低代价函数值，从而降低误判率的过程，通过对大量实际采集数据的训练，可以不断提高均衡器的准确性。在开始模型的训练前，需要先选定优化的代价函数。softmax回归模型采用极大似然估计的方法来求解模型的参数，代价函数为：

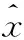
(3)

式中，m表示训练网络所用的样本总数。1{*}函数为一个特殊函数，当其参数为真时返回1，否则返回0。将式(1)代入式(3)可以得到：

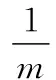
(4)

根据式(4)很难直接求解代价函数的极小值点，但是由于代价函数并非严格非凸函数，因此，可以利用梯度下降的方法来求解代价函数的极小值点，表示为：

(5)

通过式(5)，可以计算损失函数的梯度方向，在每一次样本训练结束后，沿着代价函数的梯度方向更新模型的参数ω直到收敛。经过训练迭代，不断降低代价函数的值，直到代价函数J(ω)收敛，并将这组参数ω作为系统的参数[11]。

2 卷积神经网络结构设计

卷积神经网络[12]是一种前馈人工神经网络，最初在图像识别[13]领域取得广泛应用。卷积神经网络通过卷积层遍历每个样本的方式，能够有效地提取出样本中的特征，克服非线性变换对样本特征的影响。在实际的无线通信系统中，也面临着非线性时变系统响应的问题。传统的信道均衡方法往往无法考虑信道的非线性时变特性对信号传输的影响。我们可以利用卷积神经网络模拟非线性系统的能力来提升信道均衡的性能。

图2是为信道均衡问题设计的神经网络。网络的输入层为接收天线得到的信号通过固定长度的滑动窗口采集下来的训练数据。具体而言，每个输入样本的大小都为2×N，其中N表示滑动窗口的长度，2表示分别采集信号的实部与虚部。输入层后接了两个卷积层。卷积层是卷积神经网络中最关键的环节，用于提取输入样本的特征[14]，每个卷积层都有若干个不同的卷积核。如图3所示，每个卷积核都会以一定的步长遍历整个卷积层输入并进行卷积运算。每一个卷积核都会生成一张特征图，这就是卷积层提取特征的过程。

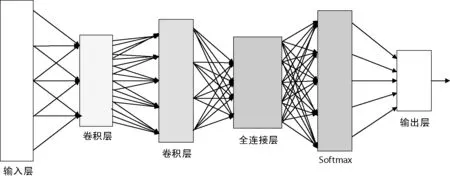
图2 卷积神经网络结构

图3 卷积层示意图

卷积运算的结果并不会直接存储在神经网络中，而是通过一个激活函数进行计算后作为特征保存下来。常用的激活函数有Sigmoid函数，ReLU函数，tanh函数[15]等。Sigmoid函数适用于特征相差不是特别大时，tanh函数适合于特征相差比较明显的样本，而ReLU函数适用于特征较为稀疏的情况[16]。本文在卷积层选择tanh函数作为激活函数，而在全连接层采用ReLU函数作为激活函数。

在构建网络的过程中，需要注意卷积核的大小决定了神经感受野的大小。卷积核过大或过小，都将导致无法提取有效的局部特征。除卷积核的大小外，卷积核的个数，卷积核移动的步长等，都是需要调整的关键参数。第二个卷积层的结构与第一个卷积层类似，也存在若干个不同的卷积核。神经网络通过级联卷积层的方式扩大感知野的范围。

神经网络在最后接入softmax层以计算当前样本在网络中被判为每个类别的概率。每次训练后，都将softmax层的输出与样本对应的真实类别向量进行比较，并利用梯度下降法更新网络参数，经过不断的训练可以提升网络的性能。

3 实 验

3.1 数据采集

为了保证测试数据的真实性和均衡算法的可靠性，同时保证采集数据的多样化，本文在多个典型室内通信环境下分别采集无线信道数据，并在各个不同数据集上对算法进行测试。如图4所示，本文用一种并行架构的信道探测仪在一些典型的室内无线通信环境中采集了大量数据。

图4 数据采集设备与环境

本文采用QPSK调制信号作为发送信号，并在发送端叠加-10～20 dB的噪声。每次采集过程以100 M/s的码片速率连续发送4 096个QPSK码片200次，并将相应的收发数据以TDMS文件的形式存储在本地。并行信道探测仪主要组件如表1所示。

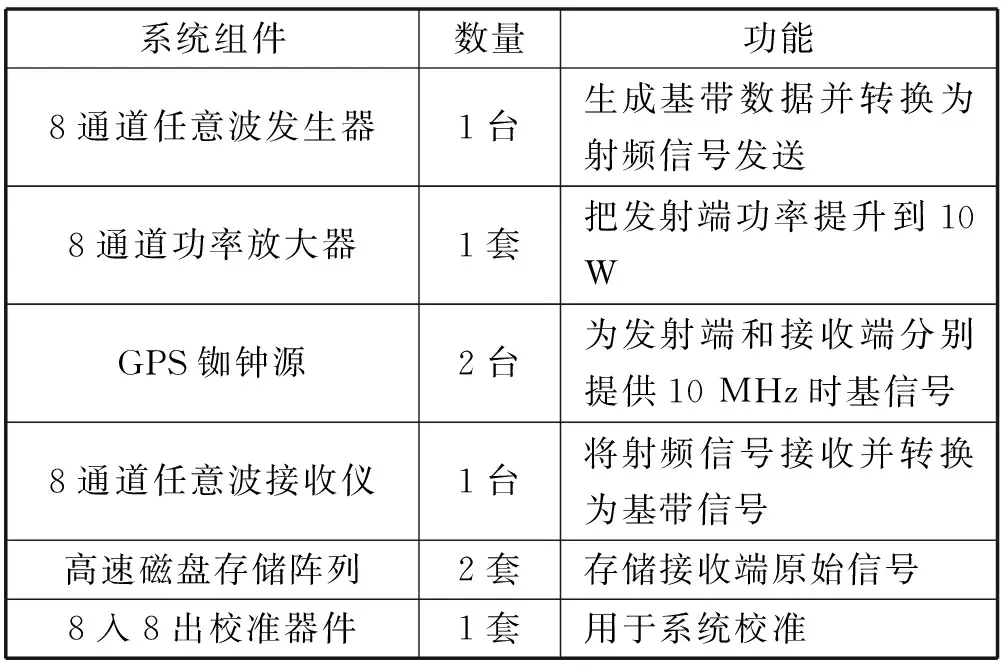
表1 并行信道探测仪主要组件

3.2 实验结果与分析

完成数据采集后，将各个数据集最后的五分之一分割出来作为测试集，剩余的部分作为训练集。其中训练集用于训练卷积神经网络以计算网络参数，测试集用于对训练后的深度神经网络进行测试以验证算法的有效性。本文还在相同数据集上使用RLS和MLP算法进行对比了实验。图5为在信噪比为20 dB的环境下，三种算法训练的均衡器从接收信号恢复出来的星座图。从图中可以看出，在20 dB信噪比环境下，基于神经网络算法恢复出来的星座图比RLS恢复出来的星座图收敛的更好。需要注意，由于CNN算法使用的是softmax分类模型，其恢复出的符号将被固定在星座图上特定的位置。

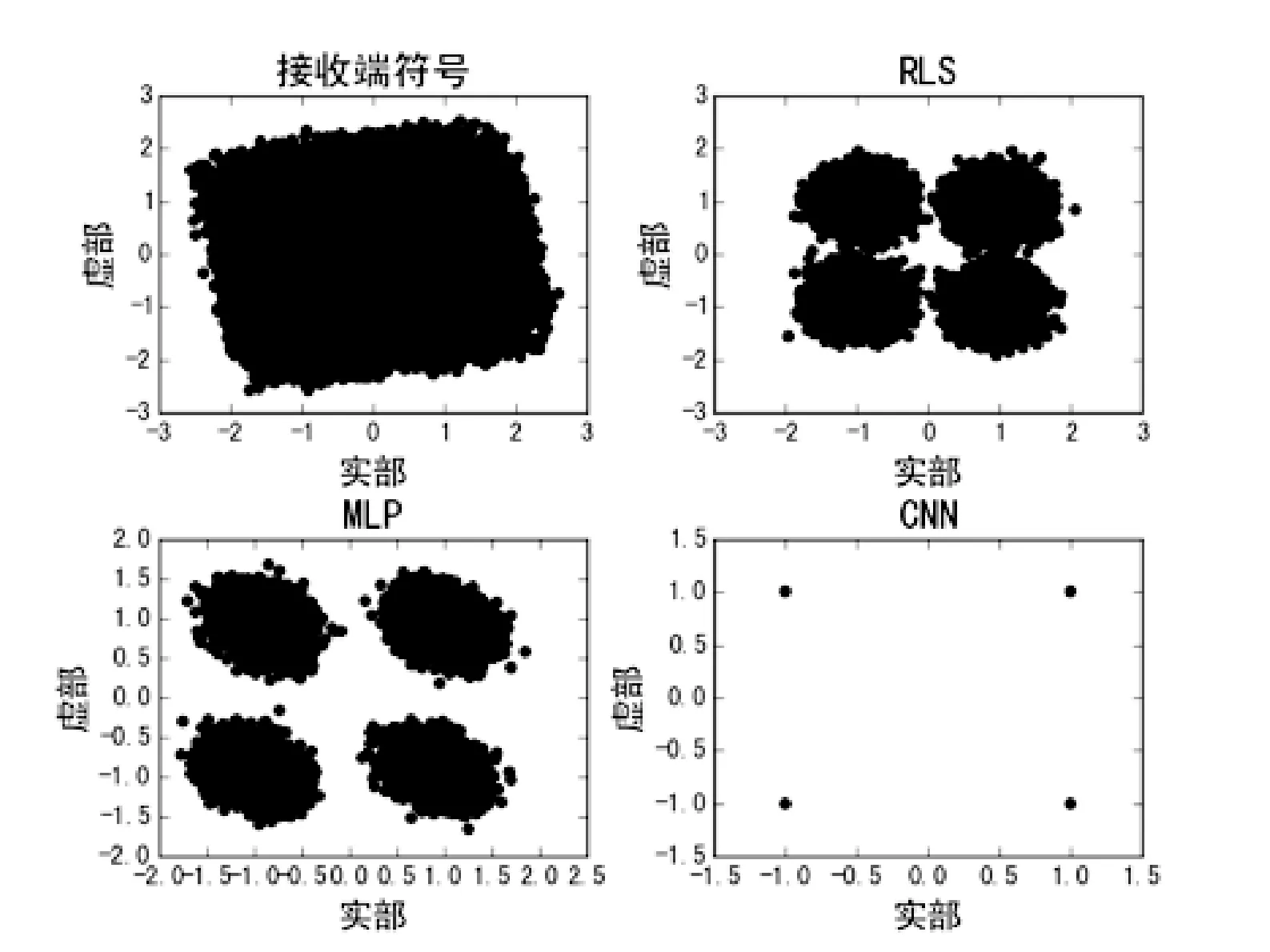
图5 RLS,MLP以及CNN恢复信号的星座

为了能够更直观地表现这三种信道均衡算法的准确性，分别对信噪比-10～20 dB范围内的数据集进行了实验，并记录不同信噪比环境下三种算法恢复信号所得到的误符号率。结果如图6所示。

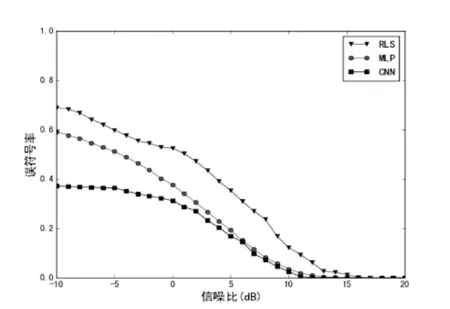
图6 不同信噪比下的误符号率

从图中可以看到，在不同的信噪比环境下，CNN的误符号率都要低于MLP和RLS。当信噪比低于0 dB时，RLS和MLP算法误符号率都很高，几乎不能恢复出发送符号，CNN得到的误符号率要低于另外两种算法，但是也不理想。当信噪比在0 dB到15 dB范围内时，三种算法的误符号率都随着信噪比的提高而有所降低，但是RLS的误符号率还是明显高于另外两种算法。同时，CNN的误符号率始终比MLP低，并且随着信噪比的提升，两者的误符号率越来越接近。当信噪比在10 dB以上时，三种算法都能够达到接近于0的误符号率。

如前文所述，卷积核的大小对卷积神经网络的性能有着至关重要的影响。在卷积神经网络的设计中，调节卷积核的尺寸是研究人员非常重要的一项工作。本文分别尝试使用多种不同尺寸的卷积核来构建卷积层，并使用信噪比为5 dB时采集的无线数据进行测试。实验结果如表2所示。

表2 不同尺寸卷积核的测试结果

从表2中可以看出，当卷积核较小时，无法准确提取特征，而当卷积核过大时，准确性并没有提升，并且由于卷积计算的复杂度变大，影响算法性能。

除了卷积核大小之外，另一个对卷积神经网络性能影响较大的参数是训练集的大小。本文分别使用多个信噪比为5 dB的不同大小的训练集对神经网络进行训练，实验结果如表3所示。

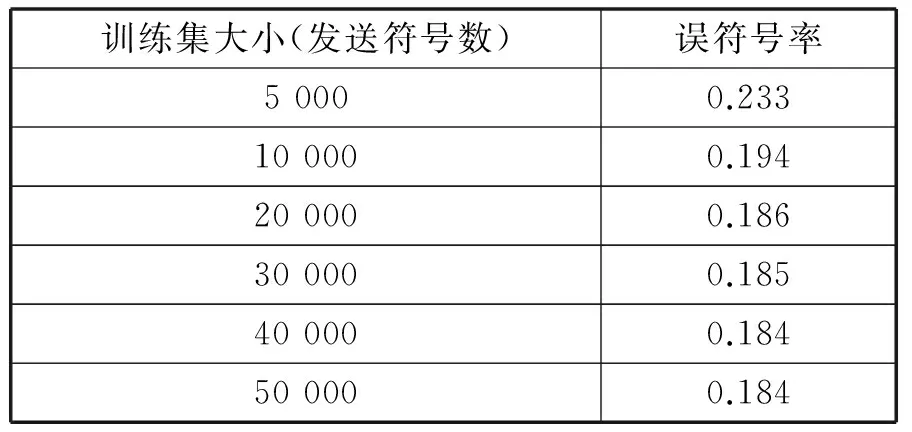
表3 不同训练集的测试结果

实验结果表明，训练集越大，训练的效果越好，但是当训练集大小超过20 000后，继续提高训练集大小并不能明显提高神经网络的性能，反而会增加训练过程的计算复杂度。

4 结 语

本文提出了一种基于卷积神经网络的算法来解决非线性时变信道的均衡问题，并在实际的通信系统中采集QPSK调制的发送符号序列及接收符号序列组成的数据集，用来训练卷积神经网络。实验结果表明，相比RLS算法以及MLP算法，卷积神经网络能够更好地处理真实通信环境中非线性时变信道的均衡，在信噪比较低的情况下能够达到更低的误符号率。如何通过网络结构的调整优化算法的计算复杂度将是我们下一步的研究方向。

[1] Umer M.Adaptive LMS Based Channel Equalization[J].International Journal of Technology and Research,2014,2(4):111-113.

[2] Sahoo S K,Mohanty M N.Effect of BER Performance in RLS Adaptive Equalizer[J].International Journal of Advanced Computer Research (IJACR),2012,2(4):208-211.

[3] Singh J M,Khan A,Gupta A,et al.Performance evaluation of CMA blind channel equalization for 4-QAM modulation[J].International Journal of Emerging Trends & Technology in Computer Science,2014,3(2):117-120.

[4] Silva M T M,Arenas-Garcia J.A soft-switching blind equalization scheme via convex combination of adaptive filters[J].IEEE Transactions on Signal Processing,2013,61(5):1171-1182.

[5] Lavania S,Kumam B,Matey P S,et al.Adaptive channel equalization using recurrent neural network under SUI channel model[C]//Innovations in Information,Embedded and Communication Systems (ICIIECS),2015 International Conference on.IEEE,2015:1-6.

[6] Das G,Pattnaik P K,Padhy S K.Artificial Neural Network trained by Particle Swarm Optimization for nonlinear channel equalization[J].Expert Systems with Applications,2014,41(7):3491-3496.

[7] Panda S,Mohapatra P K,Panigrahi S P.A new training scheme for neural networks and application in non-linear channel equalization[J].Applied Soft Computing,2015,27:47-52.

[8] Sarker M A L,Lee M H,Chung J G.ISI Free Channel Equalization for Future 5G Mobile Terminal Using Bio-inspired Neural Networks[J].Wireless Personal Communications,2015,83(4):2899-2923.

[9] Haigh P A,Ghassemlooy Z,Rajbhandari S,et al.Visible light communications:170 Mb/s using an artificial neural network equalizer in a low bandwidth white light configuration[J].Journal of Lightwave Technology,2014,32(9):1807-1813.

[10] Taddy M.Distributed multinomial regression[J].The Annals of Applied Statistics,2015,9(3):1394-1414.

[11] Reverdy P,Leonard N E. Parameter Estimation in Softmax Decision-Making Models With Linear Objective Functions[J].IEEE Transactions on Automation Science & Engineering,2015,13(1):54-67.

[12] 李彦冬,郝宗波,雷航.卷积神经网络研究综述[J].计算机应用,2016,36(9):2508-2515.

[13] Krizhevsky A,Sutskever I,Hinton G E.Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems,2012:1097-1105.

[14] Klein B,Wolf L,Afek Y.A Dynamic Convolutional Layer for short range-weather prediction[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Boston,MA,2015:4840-4848.

[15] Lecun Y,Bengio Y,Hinton G.Deep learning[J].Nature,2015,521(7553):436-444.

[16] 尹宝才,王文通,王立春.深度学习研究综述[J].北京工业大学学报,2015,41(1):48-59.

CHANNELEQUALIZATIONALGORITHMBASEDONCONVOLUTIONALNEURALNETWORK

Chen Minhua Li Yang Zhang Wuxiong

(ShanghaiInstituteofMicrosystemandInformationTechnology,ChineseAcademyofSciences,Shanghai201210,China)

In modern wireless communication system, in order to reduce the influences of InterSymbol Interference (ISI) introduced by nonlinear channel and multipath effect and solve the problem that the traditional channel equalizer cannot adapt to time-varying signals, a channel equalization algorithm based on convolutional neural network (CNN) is proposed. The quadrature phase shift keying (QPSK) dataset collected from the transmitting side and the receiving side of real wireless communication system is split into training set and test set to train and test the CNN algorithm. We thus conclude that the SER performance for QPSK systems with the CNN equalizer outperforms that of recursive least square (RLS) and multilayer perceptron (MLP) by in average 20% and 5% at low signal to noise ratio.

Channel equalization Convolutional neural network Wireless communication Deep learning

TP183

A

10.3969/j.issn.1000-386x.2017.09.050

2016-11-12。国家自然科学基金项目(61471346)；国家科技重大专项(2014ZX03005001)；上海市自然科学基金项目(14ZR1439700)。陈敏华，硕士生，主研领域：数据挖掘。李杨，博士生。张武雄，博士。