一种基于深度网络的多环境因素降水量预报模型

张鹏程 张 雷 王继民

(河海大学计算机学院 江苏 南京 211100)

一种基于深度网络的多环境因素降水量预报模型

张鹏程 张 雷 王继民

(河海大学计算机学院 江苏 南京 211100)

为了更好地反映区域降水的变化趋势，开展区域降水量预报显得尤为重要。在流域信息时代存在丰富大数据的情况下，提出一种基于DBN (Deep Belief Nets)深度网络降水量预报模型的新方案。该方案通过模拟大脑神经元的多层结构，并使用反向传播网络对整个网络进行微调。模型使用了与每日降水量息息相关的七种环境因素作为输入向量，未来24小时降水作为输出向量，通过在贵州遵义地区的实验证明了模型的有效性，并与现有方法进行了对比实验，结果表明模型具有更好的预测效果。

降水量预报 深度学习 多元时间序列 大数据

0 引 言

随着人口的急剧膨胀，河流的污染程度也随之上升，如何充分利用好地球上宝贵的水资源，是人类所面临的严峻问题。降水作为水文系统循环过程中的一个非常重要的环节，在整个水循环中起着关键性的作用[1]。降水量在较短时间内的剧烈变化，极易引发区域环境的旱涝灾害，从而对整个区域的经济发展造成严重的危害，如何更好地对未来降水量进行精准预测，是目前水信息领域急需解决的关键问题之一[2]。

降水量的预测在近几十年取得了较大的发展，常使用的一类模型是物理统计模型[3]，即选择的因子具有一定的物理意义，并利用前兆信息因子与后期汛期的遥相关原理，对降水的轻重程度进行划分。陈菊英等[4]提出了一种海河流域分区汛期降水量的多级预报物理模型，集成了各种前兆敏感信息因子，并挑选水文站的信息进行综合分析。马振锋等[5]提出的一种预测川渝地区汛期降水量的物理统计模型，利用四川盆地固有三类降水分布型的特征，得到川渝地区主汛期降水和预测中强信号的关联，建立了针对川渝地区的物理统计模型。然而物理统计模型对数据的质量要求严格，区域所处地域对预测效果影响极大，在实际的使用中不够灵活，易受不稳定因素的影响，其类似于线性刻画的建模方式，并不能很稳定地去预测降水量，存在较大的随机性。

另一类常用在降水量预测中的是数据驱动模型，数据驱动模型是以系统的状态变量作为模型的输入和输出，以建立状态变量之间的对应关系。BOX等[6]在1976年提出了给基于自回归滑动平均模型ARIMA(Autoregressive Integrated Moving Average Model)的时间序列预测方法，ARIMA模型作为使用范围较广的时间序列预测模型，先使用差分使序列平稳化，然后利用预测时刻之前单元值的预测误差或随机干扰的线性组合，对将来的时刻进行估计，但ARIMA模型用在水文序列这种受众多干扰因素影响的时间序列中，其描述能力就显得捉襟见肘，使得预测的精度较差。廖捷等[7]提出了使用马尔科夫链来预测降水的方法，通过求得各个状态概率的向量，预测结果即为概率最大值，当使用马尔科夫链去预测时，仅仅使用了一步转移概率，并没有考虑到降水时序的依赖关系。

使用人工神经网络对时间序列预测由来已久，人工神经网络一般分为多层感知机MLP(Multilayer Perceptron)、递归神经网络RNN(Recursive Neural Network)、径向基神经网络以及它们的变体形式。如季刚等[8]提出了使用径向基神经网络RBF(Radial Basis Function)来对区域的降水量进行预测，而浅层神经网络易陷入局部最小值，易过拟合，导致在预测时，模型的预测效果极不稳定，大大影响了在实际工作的使用。

深度学习作为一种模拟人类的大脑，使用多层感知网络来识别数据特征的学习算法，可以通过训练海量的数据，精准地捕捉到潜藏在其中的规律，在特征学习方面具有较强的学习能力[9-10]，较好地吻合了水文时间序列中受影响因素众多，以及难以用线性模型去表达其规律的多变性。近年来，深度网络作为数据挖掘以及机器学习的一个热点，研究主要集中在语音识别、人脸建模、字符上下文推测等方面[11-12]。每日的降水作为一个随机事件，在较长时间范围内又具有一定的规律，降水过程本身受到大量不确定因素的影响，如：区域所处气候带、太阳黑子、潮汐、大气环流以及人类自身的活动因素。因其本身存在隐藏的时序特征，呈现为一种较为复杂的非线性动力系统，使得很难找到一个合适的模型去预测未来降水量的变化趋势。每日的降水量具有数据量大、特征多、规律较难学习等特点，十分适合使用深度网络来对其学习。鉴于此，本文提出了一种基于深度网络的降水量预报模型，并通过实验发现深度网络的预测结果明显高于其他未对数据进行特征学习的浅层模型，从而验证了深度网络可以应用于降水预报。

1 基于DBN网络的降雨量预报模型

1.1 整体流程

模型的整体框架图如图1所示，大体上可以将其分为三部分。

图1 整体框架图

步骤一收集数据和数据预处理。对收集到的数据进行归一化，并对其进行KMO测试以及Barlett球形测试[13],测试是用来判断数据是否适合使用因子分析法[14](具体步骤见3.2节),通过测试之后，从序列中提取合适的因子，最后计算出提取出因子之后所有因子的信息存留量。

步骤二模型的初始化与训练。初始化网络权重，逐步训练网络，最后通过顶层BP网络反向微调。将步骤一筛选出的环境因子作为网络层的输入，计算出第一层网络的参数，再通过CD算法(见2.3节算法部分)将第一层的隐含层当作第二层的可视层计算出其余各层的系数。待所有层网络训练完毕，将降雨量作为模型的输出,使用BP网络对整个网络进行反向微调，确保模型的精确性。使用无监督学习的特点在于可以有效地提取特征，并且深度网络的拟合能力大大好于浅层网络，有效地避免了模型欠拟合的问题。

步骤三预测未来时刻降雨量。令测试样本作为模型的输入，并反归一化模型的输出。

1.2 模型基础与原理

如图2所示，深度信念网络分为两大部分，第一部分是由多层受限玻尔兹曼机RBM(Restricted Boltzmann Machine)联合而成，第二部分是顶层的BP网络，对下面的RBM层进行微调。由Smolensky等[15]提出的RBM是一种很特殊的拓扑结构，它对玻尔兹曼机BM(Boltzmann Machine)网络进行了优化，去除了层内节点之间的互联关系，大大加快了计算网络节点概率的速度。BM是一种能量网络，主要用来描述变量与变量之间的高阶相互作用，多层RBM层联结起来对数据进行无监督学习。RBM由一层可视层V(Visible layer)与一层隐含层H(Hidden layer)连接组成，可视层V用来接收特征数据，而隐含层H作为特征检测器，抽象出数据中的特征，层内节点之间没有连接关系，计算每个节点概率时可以相互独立。

图2 DBN网络结构图

对于能量函数而言，能量越低，状态越稳定，使用一段信息从可视层传送到隐含层，在传送的过程中难以避免地会出现信息不对等的情况。网络训练目标是使传送时信息尽可能的保留，通过调整偏置和权值使得可视层v与隐含层h之间的能量差异最小化，让隐含层从某种程度代表可视层，隐含层便成为可视层v的特征表示，RBM网络权值更新的公式为：

ΔWij=ε{〈vihj〉data-〈vihj〉recon}

(1)

ε是网络学习的速率，〈vihj〉data表示对于在可见层v上i节点与隐含层h上j节点所指定下分布的期望，〈vihj〉data-〈vihj〉recon表示从可见层到隐含层之间的差距，乘以学习速率对形成的能量函数进行更新。最初的深度信念网络中，RBM层都是由二值节点{0,1}组成的，由于本文的输入数据都是与气候环境相关的实值因子，二值单元的表达能力不足以表示出全部的信息，极易造成信息的丢失，故需先对输入向量进行处理。主流的处理方式分为由Hinton等[16]提出的将输入的信息直接编码为Bernoulli型，以及由Schölkopft等[17]提出的对RBM能量函数进行修改，使高斯分布直接嵌入到模型中。第一种方式会使序列中增加不必要的噪声。本文采用对RBM能量函数进行修改的方式，其中σ是关于可视层节点i高斯噪声的标准差,修改后的表达方程式为：

(2)

1.3 DBN模型算法与分析

具有深度结构的网络在提取或者表达高维数据的抽象特征时，具有强大的能力[18-19]。深度网络在分类、人脸识别以及自然语言处理中使用较广，目前在回归预测方面使用较少，本文提出了一种如图2所示的DBN网络模型对区域的降水量做回归预测。

DBN中的多层玻尔兹曼机中，第一层的可视层节点数量由与之相连接的输入样本特征数决定。DBN的网络深度对整个模型的预测性能影响较大，若RBM的层数过少，则不能充分地挖掘出时间序列中的有用信息。深度越深越有可能挖掘出序列中高层次的特征表示，层数过高也会导致对序列过度抽象，影响了网络的泛化能力[20]。

本文采用了Hinton等[21]提出的快速逐层训练的方法，即先训练好第一层RBM层，固定住它的权重，使第一层RBM的隐含层作为第二层RBM的可视层，如此分层训练，直至最后一层。后一层的RBM网络对前一层提取过特征的RBM网络进行再次抽象，从特征中提取特征，顶层设立了监督层来对整个网络进行微调(Fine-Tuning)。由于前层的无监督学习，已经使权重接近于全局最优[22]，此时使用BP网络中梯度下降法来反向微调，极大地加快了网络的收敛速度，并克服了当层数增多，无法对权值及偏置进行调整，以及网络在拟合过程中易陷入局部最小值的问题[23]。DBN网络的训练步骤如下所示：

算法1Train DBN For Hydrologic Time Series

input：区域每日的环境因素数组X(t);

output：未来24小时的降水量Y(t);

vi为可视层的单元节点;

hj为隐含层的单元节点;

W为RBM网络的权重矩阵;

K是一个用来表示评价周期的常量;

b为可视层节点的偏移量;

c为隐含层节点的偏移量;

α为阈值常数;

k为迭代次数;

l为RBM的层数;

ε为学习速率，i为等于0的常数;

mse为网络输出值以及训练样本实际值的误差;

//对输入数据和输出数据归一化

2.初始化W,b,c等各参数;

3.t=5;

无监督学习：

//训练第一层RBM网络

4.whilet>αdo

10.t=A′(v,h)-A(v,h);

11.end while

//训练其余的RBM网络

12.fori=2 toldo

13. 将i-1层RMB网络的隐含层赋值给i层的可视层；

14. 对i层RBM网络重复步骤3至15；

15.end for

有监督学习：

16.whilemse>α&&i小于一定的次数do

17. 使用BP算法调整前层网络权值；

18. 前向传播网络并计算出新的mse；

19.i++;

20.end while

2 实例分析

2.1 指标选取及网络结构选定

本文使用台站号为57713的贵州遵义1956年-2006年间的数据作为实验数据，按照10∶1的比例对数据集进行划分，保证训练数据的充分性，其中1956年—2000年作为模型的训练数据，2000年之后的数据作为测试数据，数据来自于国家气象信息中心。图3是遵义地区每日降水量折线图，从短期看来曲线杂乱无章，但从长远看来，曲线的上升和下降呈现着某种联系。

图3 日降水量走势图

本文采用均方根误差RMSE(Root Mean Square Error)以及平均绝对误差MAE(Mean Absolute Error)作为评价指标。两种指标从不同角度描述了模型对水文时间序列的刻画能力，数值越小，表明预测性能越精准，MAE的计算式表示为：

(3)

其中y(pred)i表示模型在第i天的预测结果，y(origin)i表示第i天的真实值，n表示天数。RMSE计算式表示为:

(4)

网络层数与网络节点的选取对整个网络的预测尤为重要。为了合理选取模型的结构，在选取DBN的层数时，过高的层数既影响训练的速度，又可能导致过拟合，以MAE作为评价指标，将DBN层数选取为{2,3,4}的方式来判断层数对网络性能的影响，以选取最合适的层数，如图4可见，网络层数为3时，模型的能力最佳，每层的节点分别设为{50,30,20}。

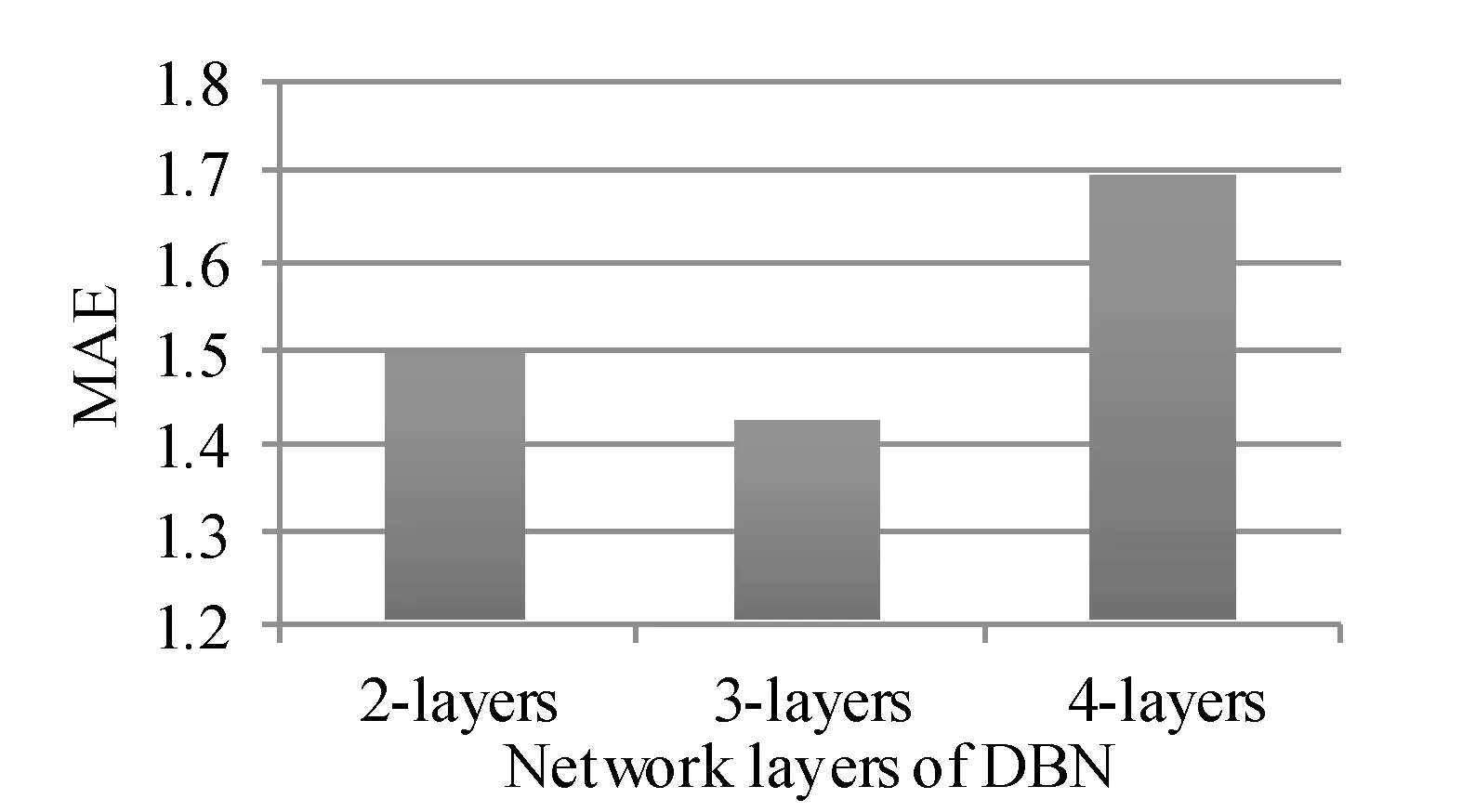
图4 RBM层数对精度的影响

2.2 环境因子的筛选

因子分析法[24]可以将原来数据中的多种指标综合成几个信息含量较丰富的指标，不仅可以解决指标之间互相相关所造成的信息重叠问题，通过因子的降维也可以减少模型训练时的计算量，加快网络收敛。本文使用因子分析对所收集的17种环境因素进行筛选，软件版本为IBM SPSS 20.0。

KMO测试以及Barlett球形测试用来判断数据源是否适合进行因子分析,KMO测试是用来表示变量之间相互关联程度的。KMO的值在0到1之间，值越接近于1，变量之间的关系越紧密，接近于0，表示变量之间的关联并不大，值小于0.5便不适宜做因子分析。Barlett球形测试是用来判断所选择的变量之间是否相互独立。

如表1所示,KMO测试的值为0.723，远远大于了0.5，证明了因子的关联性较高。卡方近似值和自由度主要与数据的维度相关，显著性为0，拒绝了零假设，表明变量之间并不是独立的。两项测试的结果都表明数据适合做因子分析。

表1 KMO测试以及Bartlett球形测试

所选取指标与原来指标之间的相互关联程度由EV(特征值)、VCR(方差贡献率)、CCR(累计贡献率)三个数值来体现。因为旋转之前相关矩阵的结构不够简明，因子对其余变量的解释能力偏弱，本文采用方差最大正交旋转变换，使因子之间更容易相互解释，如表2所示。前七的因子的累积贡献率已达到了94.2%，故选取这七个因子作为我们模型的输入，它们分别是：平均本站气压、日最高气压、平均气温、最大风速、日照时数、小型蒸发量、最小相对湿度。表3为提取了七个因子之后，所有因子的共同度，共同度指的是因子所存留的信息量。从表中可以看出，大部分的因子都保存了90%以上的信息，通过因子分析法，既保留水文序列中的信息，又避免了因子之间互相关对模型拟合造成不利影响。

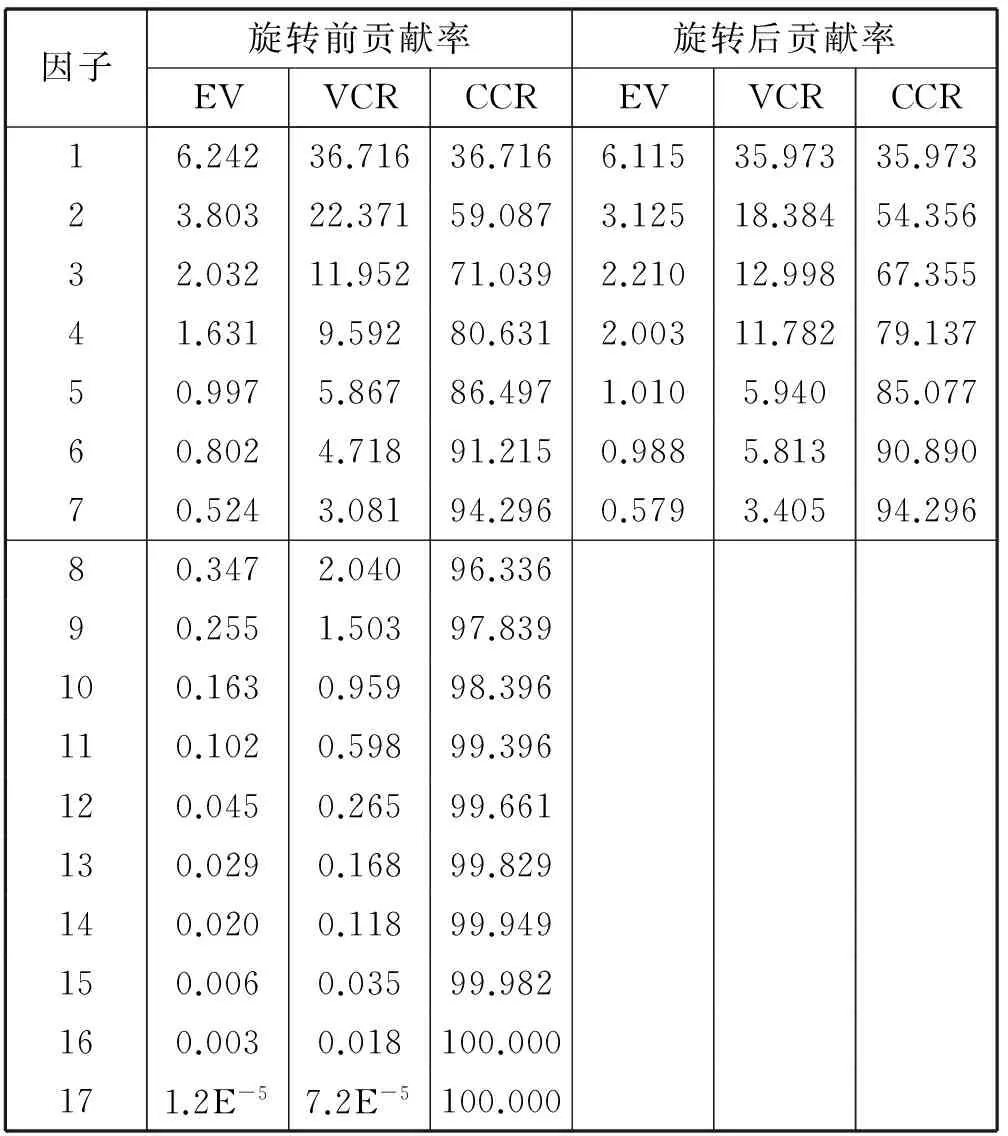
表2 相互矩阵特征值及贡献率

表3 提取因子之后的共同度

续表3

2.3 实验结果及对比分析

本文从对区域降水影响程度较大的多个环境因子筛选出7种环境因素作为模型的输入，对未来24小时的降水量进行预测。利用DBN模型所预测的降水量如图5所示。本文所使用的深度信念网络模型可以较好地对降水的趋势进行预测，对整个曲线的升降幅度的拟合也较为精确。图6将不同神经网络的迭代误差下降速度进行了对比，DBN模型误差指数在第2次迭代时已经接近了最优权值，其他两类神经网络则需要经过反复的迭代训练。

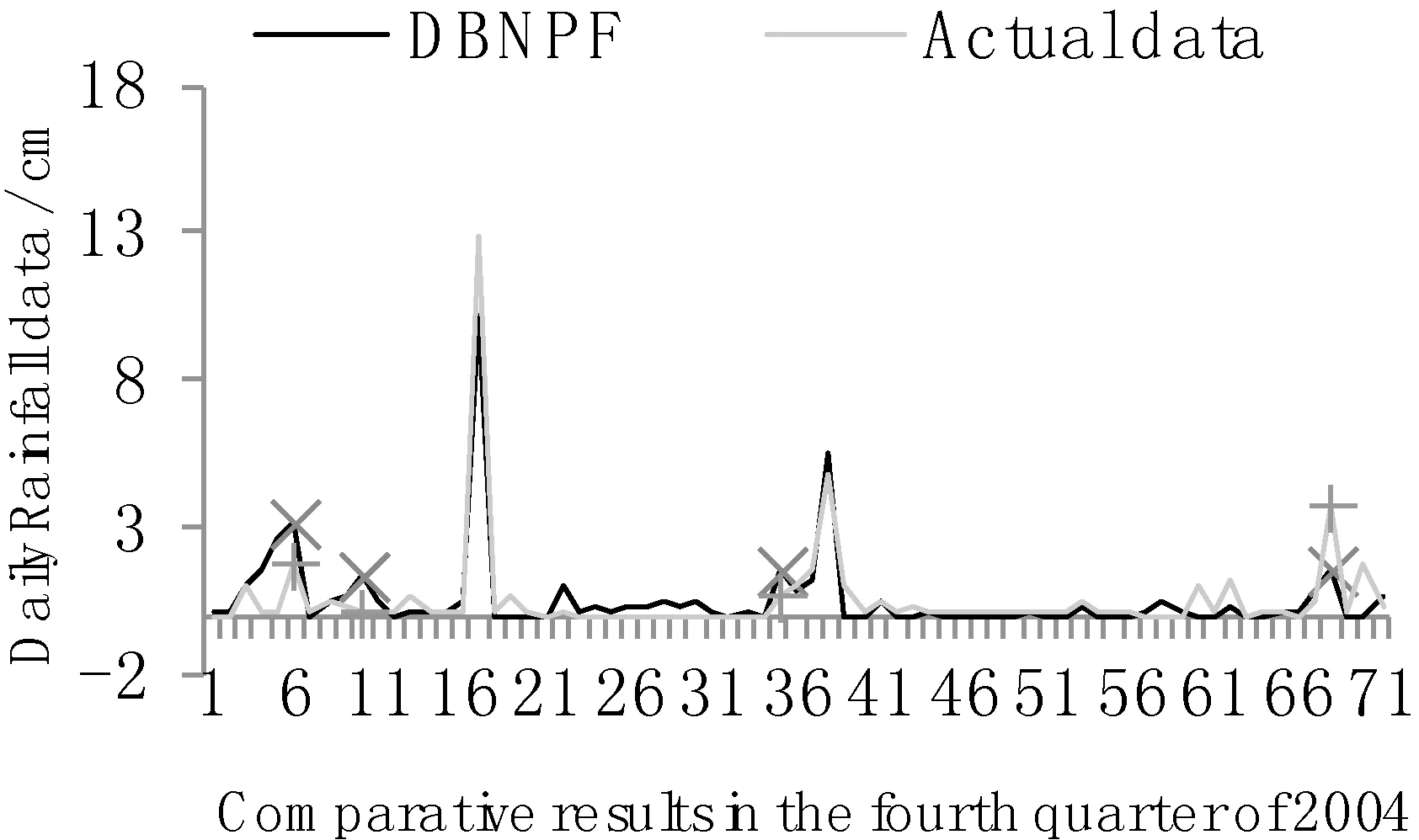
图5 DBN预测降雨与真实值对比

图6 训练误差迭代图

为了比较深度网络分析模型的拟合以及预测效果，本文将DBN降水量预报模型与经典的回归模型：径向基神经网络、支持向量机SVM、自回归滑动平均模型以及极限学习机ELM(Extreme Learning Machine)进行对比。在对比过程中，遵循单一变量原则，考虑到季节不同时，降水量的极值变化对整个网络拟合的影响，将季节分为多雨季与少雨季。图7与图8为深度信念网络与RBF模型、SVM模型在不同季节对比图。从结果可以看出，DBN模型对整个水文时间序列的拟合情况更好，对整体的趋势以及幅度波动把握也较为准确。表4和表5给出了在不同雨季五种模型具体的误差参数。从结果可以看出，在季度降水较多量较多的情况下，五种模型的误差均比少雨季大，但本文所使用的DBN模型仍然符合对降水预测的需求。

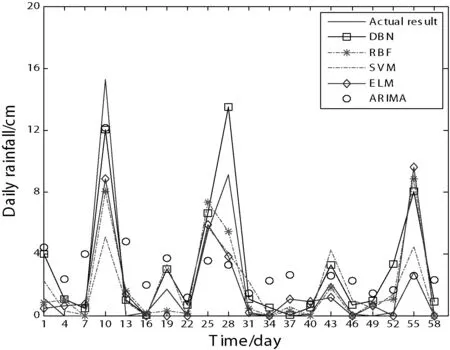
图7 多雨季模型预测对比图

图8 少雨季模型预测对比图

ModelMAERMSEDBN1.6322.257SVM2.0953.898RBF1.9393.343ARIMA3.4054.639ELM2.8593.404

表5 少雨季模型各指标对比表

3 结 语

本文针对气候环境大数据，提出了一种基于深度学习的降水量预测方案。探讨了大数据分析技术在降水预报领域的应用，结合无监督学习与有监督学习，并分析了深度网络相比较浅层神经做出的改进，实现了基于水文因子大数据的降水量预报，并通过实验验明了深度信念网络在水文时间序列上的有效性及精准性。但从目前的研究工作来看，在多雨季的预测精度仍需提高。在网络层数选取方法也应选取更为高效便捷的方式，以及采用传统预测模型筛选环境因子与深度学习相结合的方式来提高现有模型的预见期，这也将是下一步研究的重点。

[1] Wan D,Xiao Y,Zhang P,et al.Hydrological Time Series Anomaly Mining Based on Symbolization and Distance Measure[C]//IEEE International Congress on Big Data.IEEE,2014:339-346.

[2] 左洪超,吕世华,胡隐樵.中国近50年气温及降水量的变化趋势分析[J].高原气象,2004,23(2):238-244.

[3] 都金康,谢顺平,许有鹏,等.分布式降雨径流物理模型的建立和应用[J].水科学进展,2006,17(5):637-644.

[4] 陈菊英,齐晶,杨鹏,等.海河流域分区汛期降水量的多级预报物理模型的应用前景[C]//全国水文学术讨论会,2004.

[5] 马振锋,谭友邦.预测川渝地区汛期降水量的一种物理统计模型[J].大气科学,2004,28(1):138-145.

[6] Box G E P,Jenkins G M.Time Series Analysis:Forecasting and Control[J].Journal of Time,2010,31(4):303-303.

[7] 廖捷,胡豪然,陈功.叠加马尔科夫链在年降水量预测中的应用[J].安徽农业科学,2012,40(9):5532-5533.

[8] 季刚,姚艳,江双五.基于径向基神经网络的月降水量预测模型研究[J].计算机技术与发展,2013(12):186-189.

[9] Crone S F,Hibon M,Nikolopoulos K.Advances in forecasting with neural networks? Empirical evidence from the NN3 competition on time series prediction[J].International Journal of Forecasting,2011,27(3):635-660.

[10] Deng L.A tutorial survey of architectures,algorithms,and applications for deep learning[J].Apsipa Transactions on Signal & Information Processing,2014,3.

[11] Bengio Y,Delalleau O.On the Expressive Power of Deep Architectures[M]//Algorithmic Learning Theory.Springer Berlin Heidelberg,2011:18-36.

[12] Sun Z Y,Cheng-Xiang L U,Shi Z Z,et al.Research and Advances on Deep Learning[J].Computer Science,2016,43(2).

[13] Costello A B,Osborne J W.Best practices in exploratory factor analysis:four recommendations for getting the most from your analysis[J].Practical Assessment,2005,10(7):1-9.

[14] Wood P.Confirmatory Factor Analysis for Applied Research[J].American Statistician,2008,62(1):91-92.

[15] Smolensky P.On the Proper Treatment of Connectionism[M]//Readings in philosophy and cognitive science.MIT Press,1993:1-23.

[16] Hinton G E.To recognize shapes,first learn to generate images[J].Progress in Brain Research,2007,165(6):535-547.

[17] Schölkopf B,Platt J,Hofmann T.Modeling Human Motion Using Binary Latent Variables[C]//International Conference on Neural Information Processing Systems.MIT Press,2006:1345-1352.

[18] Bengio Y.Learning Deep Architectures for AI[J].Foundations & Trends® in Machine Learning,2009,2(1):1-127.

[19] Hinton G E,Osindero S,Teh Y W.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554.

[20] Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.

[21] Hinton G E.A Practical Guide to Training Restricted Boltzmann Machines[J].Momentum,2010,9(1):599-619.

[22] Ackley D H,Hinton G E,Sejnowski T J.A learning algorithm for boltzmann machines[J].Cognitive Science,1985,9(1):147-169.

[23] Rumelhart D,McClelland J.Learning and Relearning in Boltzmann Machines[M].MIT Press,1986:45-76.

[24] Sakaluk J K,Short S D.A Methodological Review of Exploratory Factor Analysis in Sexuality Research:Used Practices,Best Practices,and Data Analysis Resources[J].Journal of Sex Research,2016,54(1):1-9.

AMODELFORPRECIPITATIONFORCREASTINGOFMUTIPLEENVIRONMENTALFACTORSBASEDONDEEPNETWORK

Zhang Pengcheng Zhang Lei Wang Jimin

(SchoolofComputerScience,HohaiUniversity,Nanjing211100,Jiangsu,China)

To better reflect the changing trend of regional precipitation, it is particularly important to develop regional precipitation forecast. Therefore, in the case of abundant information in the era of basin big data, a new method of precipitation forecasting model based on DBN (Deep Belief Nets) depth network is proposed. The scheme simulated the multilayer structure of the brain neurons and adopted the back propagation network to fine tune the entire network. Besides, the model adopted seven environmental factors that were closely related to the daily precipitation as input vectors, and the next 24 hours precipitation as the output vector. The effectiveness of the proposed model is proved by experiments in Guizhou, Zunyi, and compared with the existing methods. We conclude that the model has better prediction results.

Precipitation forecasting Deep learning Multiple time Series Big data

TP391

A

10.3969/j.issn.1000-386x.2017.09.047

2017-03-01。国家自然科学基金项目(61572171)；国家科技支撑计划项目(2015BAB07B01)。张鹏程，副教授，主研领域：软件工程，数据分析与处理。张雷，硕士生。王继民，副教授。