二分搜索法求解悬链线问题
马 旭 易 俗
(辽宁大学创新创业学院 辽宁 沈阳 110036)
二分搜索法求解悬链线问题
马 旭 易 俗
(辽宁大学创新创业学院 辽宁 沈阳 110036)
悬链线问题是现代工程实践中经常遇到的问题之一。分析悬点等高及不等高两种情况下悬链系数、弛垂度、悬点水平坐标的常规数学求解方式,基于其运算量大,误差难以把握的不足,提出应用二份搜索程序设计思想辅助求解的具体思路。分别给出3种不同应用的完整程序及数据,比较分析数学方式与程序设计求解方法。以吊杆架设工程应用为实例,结合完整C语言程序及其主函数流程图 ,较详细地描述了相关各参数的程序求解过程。上述方法已多次应用于实践,是简单可行的。
二分搜索法 悬链线 悬链系数 弛垂度 误差分析 C程序设计
0 引 言
悬索吊桥、双曲拱桥、架空电缆、索道滑车等诸多实践应用中,都涉及到悬链线[1-6]。悬链线函数是超越函数,应用中可以通过查双曲函数表、抛物线逼近、级数展开求解高次方程等数学方法近似求解[7-9]。在悬链线接近水平时,常规数学运算可以满足一般工程的需要,但针对倾斜度较大的悬链线,数学运算计算繁杂,精度难以提高,更难以把握[10-12]。许多工程实践中,在指定精度要求下,利用二分搜索程序辅助求解,更为简单实用[13]。
本文将就悬链线应用中的多种实用形式,结合C语言描述,分别给出相关函数及应用程序,求解悬链系数、弛垂度、悬索链长及悬点水平坐标,并给出工程应用实例。
1 两悬点高度相同的情况
如图1所示,A、B两悬点等高,水平距离为L,悬链线链长为S,悬点与最低点垂直距离(弛垂度)为D,悬链线最低点与横轴垂直距离为a(悬链系数),x1、x2为两悬点的水平坐标。

图1 两悬点等高的悬链线坐标图
悬链线的标准方程为:
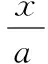
(1)
实际应用中,两悬点间水平距离一般可以预知,无论是已知链长求弛垂度,还是已知弛垂度求链长,还是在工程实践中分析悬点的受力,首要解决的问题就是求悬链系数a。
1.1 已知链长及两悬点间水平距离求弛垂度
1.1.1 常规数学方式求解弛垂度
弛垂度的标准方程为:

(2)
参考图1求解D,利用曲线积分可以得出下列结果:


(3)
求解上述超越方程,可以经过幂级数展开、麦克劳林展开、麦克劳林系数求解等一系列代数运算,在忽略高于二次的级数项后,可以近似得出下列结果[14]。
设:

(4)

(5)
则:

(6)
(7)
此公式在常规实践中是可以应用的,但在误差精度要求更高,尤其在误差精度要求随应用而调整的情况下,就很难适用了。
1.1.2 二分搜索法求解弛垂度
设有函数y=f(x),与数学求解函数的方式不同,利用二分搜索程序设计思想,预先编制搜索原函数double fun(double x)和二分搜索函数double dichotomy (double (*fp)(), double x1, double x2, double y),在一定范围(x1,x2)、一定精度要求下,即可通过二分搜索法搜索到指定函数值y对应的x(x=f-1(y)),可以有效地解决上述实际问题[15-16]。
设:
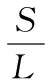
(8)

(9)
化简后可得:
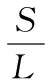
(10)
基于函数y=sinh(x)/x建立搜索原函数如下:
double funz( double x )
{ double y;
y=sinh(x)/x;
return y;
}
基于指定搜索原函数fp()、指定函数值y,在(x1,x2)区间,按指定精度要求AC,进行二分搜索,返回搜索点近似值x,二分搜索函数如下:
double dichotomy (double (*fp)(),double x1, double x2, double y)
{ double x, p;
do { x=(x1+x2)/2;
p=fp(x);
if (p>y) x2=x;
if (p } while ( fabs(p-y) > AC ); return x; } 由悬链线实践确定的数据范围可预先设定3>t>0,设Z=S/L,调用二分搜索函数dichotomy( funz, 0, 3, Z )可以搜索求得原函数Z=sinh(t)/t中t值,再利用下面公式即可求得悬链系数a及垂弛度D: (11) 1.1.3 实 例 例1:给定一组链长S、悬点间距离L,利用二分搜索法,在误差δ<10-3条件下,求悬链系数a及弛垂度D,主函数程序描述如下: #include ″stdio.h″ #include ″math.h″ #define AC 1e-3 main() { double s[5]={25,35,45,55,65}, l[5]={20,30,40,50,60}, a[5],d[5]; int i; for ( i=0; i<5; i++) { double t,p; t=dichotomy( funz, 0, 3, s[i]/l[i] ); a[i]=l[i]/(2*t); p=l[i]/(2*a[i]); d[i]=a[i]*cosh(p)-a[i]; } for ( i=0; i<5; i++) printf(″ L=%6.3f, S=%6.3f, a=%6.3f, D=%6.3f
″, l[i],s[i],a[i],d[i]); } 1.1.4 数学求解与程序求解的比较 指定精度要求为δ<10-5、δ<10-4,分别利用1.1.3节中程序求解得悬链线的弛垂度为D2、D3,通过MATLAB按1.1.1节中数学方法求得悬链线的弛垂度为D1,它们对比如表1所示。 表1 二分搜索法与常规数学方法求解驰垂度对比 参考表1可见,利用1.1.1节中数学解法求得的弛垂度D介于二分搜索程序误差设置在10-5与10-4之间。 实践中,可以在指定精度要求下,预先确定链长S与悬点距离L的比值表。具体工程中即可通过查表方式确定t值,再通过上面所述的公式求系数a、弛垂度D。查表求解更为简单实用。表2为δ<10-6时链长S与悬点距离L的比值表。 表2 链长S与悬点距离L的比值表 1.2 已知弛垂度及两悬点间水平距离求链长 1.2.1 二分搜索法求链长 设: (12) (13) 化简后可得: (14) 基于函数y=(cosh(x)-1)/x建立搜索原函数如下: double funv(double x) { double y; y=(cosh(x)-1)/x; return y; } 参照例1,在3>t>0范围内,设V=D/(L/2),调用二分搜索函数dichotomy(funv,0,3,V)搜索求解原函数V=(cosh(t)-1)/t中t值,再利用下面公式可以求得悬链系数a和链长S: (15) 1.2.2 实 例 例2:给定一组弛垂度D,悬点距离L。利用二分搜索法,在误差δ<10-3条件下,求悬链系数a及链长S,主函数程序描述如下: #include ″stdio.h″ #include ″math.h″ #define CC 1e-3 main() { double l[5]={20.000,30.000,40.000, 50.000,60.000}, d[5]={6.636,7.924,9.030,10.015,10.911},a[5], s[5]; int i; for ( i=0; i<5; i++) { double t,v,p,y; v=2*d[i]/l[i]; t=dichotomy( funv,0,3,v ); a[i]=l[i]/(2*t); p=l[i]/(2*a[i]); s[i]=2*a[i]*sinh(p); } for ( i=0; i<5; i++) printf(″L=%6.3f, D=%6.3f, a=%6.3f, S=%6.3f
″, l[i],d[i],a[i],s[i]); } 上述程序设定的初始弛垂度D为表1中的D2。指定不同精度要求(δ<10-3,δ<10-5)利用二分搜索程序求解的悬链线链长(S1,S2)与表1中初始S对比如表3所示。 表3 二分搜索法所求链长S与真实链长对比 参考表3可见,搜索程序精度设为10-3时,误差已经可以在许多实践环境中被接受,当搜索程序精度设为10-5时,误差就更小了。 2.1 二分搜索法求悬点横坐标及弛垂度 如图2所示,A、B两悬点水平距离为L,悬链线链长为S。较低的悬点A与最低点的垂直距离(弛垂度)为D,两悬点的垂直距离为H,悬链线最低点与横轴垂直距离为a,x1、x2为两悬点的水平坐标。 图2 两悬点不等高的悬链线坐标图 由悬链线标准方程,可知: (16) (17) (18) (19) (20) (21) 即: (22) 通过上式可知,在给定L、S、H时,可以通过将sinh(x)级数展开,再解高次方程求得悬链系数a,进而求得x1及弛垂度D(公式推导略)。 考虑到高次方程运算的复杂度限制,在级数展开时通常只能选取前2至3项。上述解法不但误差不好调整,在一些实际操作中也不够灵活、方便。 设: (23) 化简上式可得: (24) 设Z=sqrt(S×S+H×H)/L,调用二分搜索函数dichotomy(funz,0,3, Z)可搜索求解t,从而求得悬链系数a(函数funz()定义参照1.1.2节)。已知悬点垂直距离H推导公式: (25) 可以参见例1、例2,建立搜索函数如下: double funh(double x) { double y1,y2,x1,x2,t; x1=(x+l[i]) / a[i]; x2=x/a[i]; t=a[i]*( cosh(x1)-cosh(x2) ); return t; } 调用进行二分搜索dichotomy(funh,-3×a,3×a,H),即可求得x1,进而弛垂度D可求。 2.2 实 例 例3:给定一组链长S,悬点距离L,悬点高度差H,求解悬链系数a、弛垂度D与低点的横坐标X1,主函数程序描述如下: #include ″stdio.h″ #include ″math.h″ #define CC 1e-3 double s[5]={ 30.000, 30.000, 30.000, 90.000, 90.000 },l[5]={ 20.000, 20.000, 20.000, 60.000, 60.000 },h[5]={ 0.000, 5.000, 10.000, 0.000, 30.000 },a[5], x[5], d[5]; int i; main() { double t,z; for ( i=0; i<5; i++) { z=sqrt( s[i]*s[i]-h[i]*h[i] ) / l[i]; t=dichotomy( funz,0,3,z ); a[i]=l[i]/(2*t); x[i]=dichotomy( funh, -3*a[i], 3*a[i], h[i] ); d[i]=a[i]*( cosh(x[i]/a[i])-1 ); } for ( i=0; i<5; i++) printf(″ L=%6.3f, S=%6.3f, H=%6.3f, a=%6.3f, x=%6.3f, D=%6.3f
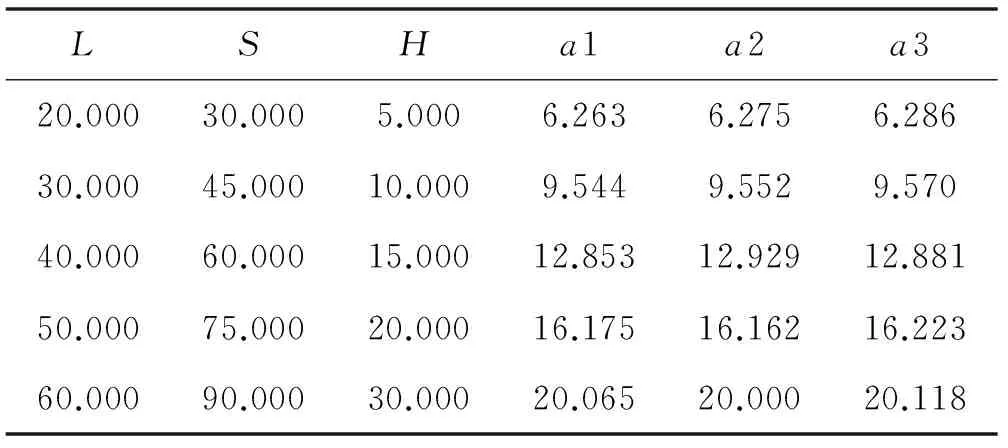
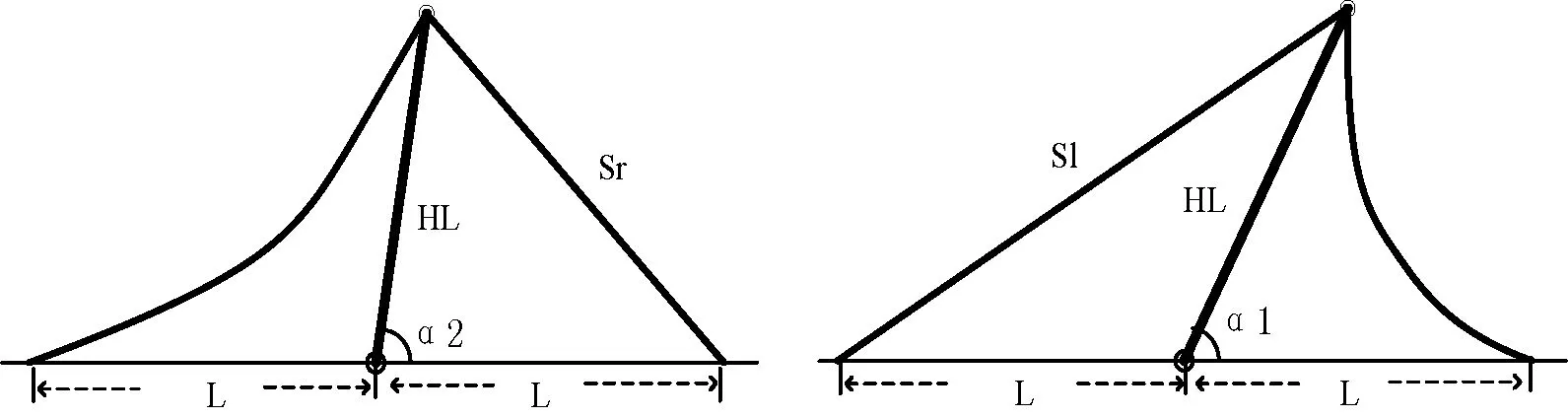
″,l[i], s[i], h[i], a[i], x[i], d[i]); } 可以借助MATLAB,按2.1节中描述的数学方法求解悬链系数a。利用二分搜索程序在δ<10-2和δ<10-3精度要求下求解的悬链系数a2和a3。与MATLAB求解的悬链系数a1对比如表4所示。 表4 二分搜索法与常规数学法求解悬链系数对比 参考表4可见,利用数学解法求得的悬链系数a介于二分搜索程序误差设置在10-2与10-3之间。表中省略了弛垂度D与低点的横坐标X1的输出。 3.1 悬点受力分析 悬链线应用实践中,悬点的受力情况是首要考虑的问题,如图3所示。 图3 悬点B受力分析 设链索线密度为ρ,则悬点B水平、垂直及切线方向受力Tx、Ty、T可表示如下: (26) (27) (28) (29) 在式(26)、式(28)中代入链长: (30) 则: (31) (32) 式(26)、式(28)、式(29)、式(31)和式(32)经常在悬链线应用中被选择使用。 3.2 悬链线应用实例—吊杆架设 在特定的地区、地势、地理等多种环境下,无法使用现代化的塔吊设施,完成货物的定点吊运只能采用传统的架设吊杆方法。 已知预吊起的货物重量WG,已具备的吊杆长度HL,吊杆重量为HG,两根链索的线密度ρ,怎样架设吊杆才能准确地将货物吊运到指定位置P处。工程实践中,可以通过多种方式将吊杆固定在两根链索的同一平面上,本例只探讨吊杆及两根链索所在平面的架设问题,图4为吊杆架设的平面图。 图4 吊杆架设平面图及受力分析 实践中常规的吊杆架设方式可有如下3种: (1) 已知左右两根链索的长度Sl与Sr,AB两点已选定,水平距离2L,吊杆架设的支点O为AB中点,求解吊杆的水平夹角α,从而确定吊杆基点O与指定吊点P的水平距离OP,可以验证链索长度是否合适。 (2) 已知左右两根链索的长度Sl与Sr,吊杆的基点位置O已选定,求解AB两点的水平距离2L,从而确定AB两点的固定位置,在选定处固定链索即可。 (3) 吊杆的基点位置O已固定,AB两点也已选定,已知一条链索的长度,求解另一条链索的长度,按要求配置链索即可。 下面仅就上述第一种架设方法给以实例说明,另外两种架设方法与之相似,本文略。 例4:已知左右两侧链索线密度ρ,A、B两点的水平距离2L,架设的吊杆长度HL,重HG。输入两根链索长度Sl、Sr,预吊起的货物重WG,求吊杆水平夹角α及货物吊点与吊杆支点水平距离PX。 分析图4可知,左右两侧悬链线悬点水平距离Ll、Lr及悬点垂直距离H分别为: Ll=L+HL×cos(α) Lr=L-HL×cos(α) H=HL×sinα 两侧悬链线系数分别为al、ar,悬点C在两侧悬链线上的水平坐标为Xl、Xr,则悬点C水平及垂直作用力Tl、Tr、Vl、Vr分别为: Tl=al×ρTr=ar×ρ 悬点C处顺时针力矩MS与逆时针力矩MN分别为: MS=Tr×HL×sinα+(Vl+Vr+0.5×HG+WG)× HL×cos(α) MN=Tl×HL×sin(α) 吊杆平衡时MS=MN,可以整理等式为: (Vl+Vr+0.5×HG+WG)×HL×cos(α)= (Tl-Tr)×HL×sin(α) 下面程序中设置: M1=(Tl-Tr)×HL×sin(α) M2=(Vl+Vr+0.5×HG+WG)×HL×cos(α) 图5为两根链索分别拉直时的吊杆平面图。 图5 吊杆角度分析图 通过余弦定理可求吊杆极限角度α1与α2: 吊杆水平角度α实际取值范围应在α1与α2之间,即α1<α<α2。 例4采用二分搜索法在α1与α2之间搜索α(本例中为变量c),函数funz()、funh()、dichotomy()可以参见前文,图6为主函数程序流程图。 图6 例4主函数流程图 例4程序描述如下: /* a、s、l、x各数组0、1元素(例如:a[0]、a[1]、s[0]、s[1]…)分别表示左[右]侧悬链线对应值,h为两条悬链线共同的悬点高度差,函数funz()与funh()定义参照例1与例3。 */ #include ″stdio.h″ #include ″math.h″ #define CC 1e-3 double s[2], h, l[2], a[2], x[2]; int i; double funz(double x) /*略*/ double funh(double x) /*略*/ double dichotomy(double (*fp)(),double x1,double x2,double p1) /*略*/ main() { double c1, c2, c, ss, p, wg, hl, hg, z, h, m1, m2, px; double t[2],v[2]; ss=100; hl=40, hg=200, p=10; printf(″Enter SL & SR :″); scanf(″%lf %lf″,&s[0],&s[1]); printf(″Enter WG= ″); scanf(″%lf″,&wg); c1=3.14-acos( (hl*hl+ss*ss/4-s[0]*s[0]) / (hl*ss) ); c2=acos( (hl*hl+ss*ss/4-s[1]*s[1]) / (hl*ss) ); do { double temp; c=(c1+c2)/2; l[0]=ss/2+hl*cos(c); l[1]=ss/2-hl*cos(c); h=hl*sin(c); for(i=0;i<2;i++) { z=sqrt(s[i]*s[i]-h*h)/l[i]; temp=dichotomy(funz,0,3,z); a[i]=l[i]/(2*temp); x[i]=dichotomy(funh, -3*a[i], 3*a[i],h); t[i]=a[i]*p; v[i]=temp*sinh((x[i]+l[i]) / a[i]); } m1=(t[0]-t[1])*hl*sin(c); m2=(v[0]+v[1]+hg/2+wg)*hl*cos(c); if (m1>m2) c1=c; else c2=c; } while ( fabs(c1-c2)>1e-6); px=hl*cos(c); printf( ″C=%6.2f,PX=%6.2f″, c/3.14*180,px); } 【程序输入】 Enter SL & SR :70 60 Enter WG :500 【程序输出】 C=78.55 PX=7.97 程序中已赋值A、B两点距离SS=100 m,吊杆长度HL=40 m、吊杆重量HG=200 kg、吊杆线密度P=10 kg/m,实验数据如表5所示。 表5 吊杆架设实验数据 实践中亦可以构造更详细的表5,根据货物重量的不同,查表调整两根链索的长度,实现吊杆的架设。 悬链线问题核心是超越函数的求解。无论是怎样的代数转换,运算量和精度要求都难以把握。实践证明,通过二分搜索程序设计辅助求解可以有效地解决上述问题,在实践中是简单可行的。 [1] 白兴兰,段梦兰,李强.基于整体分析的钢悬链线立管触地点动力响应分析[J].工程力学,2014,31(12):249-256. [2] Thethi R,Moros T.Soil interaction effects on simple catenary riser response[R].Deepwater Pipeline & Riser Technology Conference,Houston,Texas,2011:1-24. [3] 李传习,陈洪林,柯红军.空间缆索悬索桥水平母线鞍座设计位置的确定[J].中外公路,2015,25(6):90-94. [4] Nader M,Maroney B.The New San Francisco-Oakland Bay Bridge[C]//Structures Congress,2013:588-598. [5] 邱为钢.悬链线的几何特征[J].物理与工程,2015,25(3):28-34. [6] 马旭,杨文美.医疗特征图像边缘曲率分析实例[J].医学影像学杂志,2010,20(11):1713-1715. [7] 颜玉娇,尚伟伟.6自由度绳索牵引并联机器人的悬链线建模与动力学分析[J].中国科学技术大学学报,2015,45(7):546-554. [8] Zi B,Ding H F,Cao J B,et al.Integrated mechanism design and control for completely restrained hybrid-driven based cable paralled manipulators[J].Journal of Intellignent and Robotic Systems,2014,74(34):643-661. [9] 王丹,刘家新.一般状态下悬链线方程的应用[J].船海工程,2007,36(3):26-28. [10] 王建国,逄焕平,李雪峰.悬索桥线形分析的悬链线单元法[J].应用力学学报,2008,25(4):626-631. [11] 王长昌.基于悬链线方程的跨接电缆长度计算[J].铁道车辆,2013,51(6) 4-6,33. [12] 陈常松,陈政清,颜东煌.悬索桥主缆初始位形的悬链线方程精细迭代分析法[J].工程力学,2006,23(8):62-68. [13] 马旭,张寿鹏.一种基于弧长与弦高的半径函数逼近算法[J].辽宁大学学报,2016,43(2):130-133. [14] 邢富冲.悬链线弛垂度的计算方法[J].数学的实践与认识,2004,34(11):98-101. [15] 马旭,王大勇.趣味智能模拟程序设计实例[J].计算机与数字工程,2016,44(5):979-982. [16] 林贵瑜,冯优达,苑登波.钢丝绳抛物线理论与悬链线理论的计算误差分析[J].建筑机械化,2010(3):42-43,55. BINARYSEARCHMETHODFORSOLVINGCATENARYPROBLEM Ma Xu Yi Su (SchoolofInnovationandEntrepreneurship,LiaoningUniversity,Shenyang110036,Liaoning,China) Catenary problem is one of the problems often encountered in modern engineering practice. In the two cases that two hanging points at the same height and different heights, the paper analyzes the conventional mathematical methods for solving the catenary coefficient, sag and the abscissa of the hanging points. Due to the large amount of calculation and the error is difficult to grasp, the paper proposes the binary search programming specific ideas to assist in solving, and offers three complete programs and data for different applications, compares and analyzes the mathematical methods and programming methods. Taking the boom erection project as an example, the paper provides a complete C program and the main function flowchart, and describes in more detail the procedures to solve the relevant parameters. The above method has been applied to practice many times, and it is simple and feasible. Binary search method Catenary Catenary coefficient Sag Error analysis C programming TP39 A 10.3969/j.issn.1000-386x.2017.09.011 2016-11-28。国家自然科学基金项目(11304135);辽宁省自然科学基金项目(201602345);沈阳市应用基础研究专项项目(F15-199-1-04)。马旭,高级实验师,主研领域:计算机应用,人工智能。易俗,实验师。



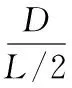

2 两悬点高度不同的情况









3 悬链线应用实例






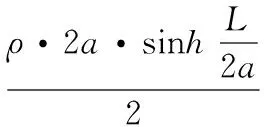








4 结 语

