分布式发电配电网故障区段定位新方法
郭 玉 雯
(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105)
分布式发电配电网故障区段定位新方法
郭 玉 雯
(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105)
针对分布式电源引入配电网中会造成传统的故障区段定位方法不再适用的情况,构建动态适应多个分布式电源投切的开关函数,且利用该开关函数的特点可以简化运算,提高定位效率。同时,针对蚁群算法容易出现早熟收敛的问题,引入混合优化算法,提出基于混合优化算法的分布式发电配电网故障定位方法。该算法利用粒子群算法优化蚁群算法中的相应参数,采用全局异步与精英策略相结合的信息素更新方式和降低粒子维度的方法降低出现局部最优解的概率,提高了收敛速度和定位结果的正确率。通过典型算例对含分布式电源的配电网进行仿真,实验结果表明该算法能够对单一故障和多重故障准确定位,且耗时少、容错能力强。
分布式电源 配电网 混合优化算法 开关函数
0 引 言
在配电网中,快速准确地对故障区段进行定位是隔离与恢复非故障区域正常供电状态的前提。目前,利用FTU(Feeder Terminal Unit)搜集的信息进行故障定位的人工智能算法主要包括蚁群算法[1-2],遗传算法[3-5]以及和声算法[6-7]等。其中,利用蚁群算法进行配电网故障定位的核心就是旅行商问题,针对该问题的研究已经获得了大量成果。由于蚁群算法运行初期信息素匮乏及参数选择不当,其收敛速度慢,导致“早熟收敛”发生。针对该问题,文献[8-9]提出的基于粒子群优化的蚁群算法提高了收敛速度,但需要进一步提高收敛速度才能使算法达到最优状态,有待进一步研究。
目前,分布式发电正逐渐广泛应用于配电网中,而分布式电源的投切会造成配电网由单电源辐射式变为多电源辐射式[10-12],同时线路潮流也会发生变化,对配电网故障定位结果的正确率产生影响。因此,为了适应这些变化需要对定位数学模型进行改进。文献[1]对开关函数和评价函数的构造进行了改进,能够对多电源网络复杂故障进行定位,但未考虑分布式电源投切的影响,并且正方向不一致,需要多次设定方向。文献[13]考虑了分布式电源投切对配电网结构产生的影响,但只适用于结构简单的配电网,使用范围受限。
针对上述情况,对配电网故障区段定位模型中的开关函数和正方向的规定方法在适应分布式电源的投切,提高计算效率方面做了修整。并且,为了使收敛速度更快,算法陷入局部收敛的可能性更小,提出了一种基于蚁群粒子群混合优化算法的配电网故障区段定位方法。该方法利用改进的数学模型进行定位,在降低粒子群算法中粒子维度的同时实现系统参数的优化,进一步缩短定位时间,有效抑制“早熟收敛”现象的发生。
1 混合优化算法原理
1.1 蚁群算法
蚁群算法擅长离散优化问题的解决,已经成功运用到了TSP问题中,蚁群算法利用旅行商问题与蚂蚁搜集食物过程的相似性,即通过个体相互协作与信息交互所寻求的蚁穴至食物源的最优路径进行配电网故障区段定位。

(1)
其中,蚂蚁j下一步可以到达的城市为allowekj,allowekj={1,2,…,n}-tabuj;蚂蚁j走过的城市用集合tabuj表示,其将会随着蚂蚁的搜索进程的不断变化作出调整。ηab即由地点a转移到地点b的期望程度,根据某些启发式算法或问题的具体情况进行确定。α、β分别表示蚂蚁在运动过程中累积的信息量以及期望信息在蚂蚁所经路径的作用,α及β与蚁群算法性能密切相关。之前留下的信息素的浓度会随时间逐渐降低,用1-ρ表示信息素浓度的衰减情况,n个时刻为一个周期,信息素浓度调整公式如下:
τab(t+n)=ρτab(t)+Δτab
(2)
(3)

(4)
其中,一次循环中,Q为蚂蚁在所能释放出的总信息量且为常数,蚂蚁j所经过的路径长度为Lj。
由式(3)和式(4)可知,信息素的分布情况与保证蚁群算法的求解质量息息相关,所以,选择恰当的信息素更新方式尤为重要。同时,蚁群算法参数的选择依赖于实验者的个人经验,若出现参数选取不当的情况,会出现“早熟收敛”问题,制约了蚁群算法的最佳性能。需要对其参数优化过程进行改进。
1.2 粒子群算法
粒子群算法以多次迭代的方法搜索最优解,初始化为随机粒子,以后每次迭代中通过跟踪个体极值(当前单个粒子所寻找到的最优解)和全局最优解(当前所有粒子整体所寻找到的最优解)来不断更新自身搜索到的解,个体极值用g表示,全局最优解用q表示。第i个粒子的速度更新方程和位置更新方程如公式所示:
(5)
(6)
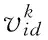
粒子群算法综合利用种群信息和个体经验更新粒子的速度和位置,擅长连续优化问题的解决,依赖经验参数少,能快速逼近最优解。但其进行全局优化时容易出现早熟收敛,局部寻优能力差等,主要原因为种群搜索空间中多样性的减少。为此,结合1.1节中的结论可以得出利用粒子群算法依赖经验参数少,能快速逼近最优解的优点与对蚁群算法相结合,吸收这两种算法的优点达到快速准确对故障定位的目的。
1.3 混合优化算法
蚁群粒子群混合优化算法使用蚁群算法进行搜索,用粒子群算法对蚁群算法中的参数进行优化,降低纯蚁群算法陷入局部最优解的概率。为了保证蚁群算法求解质量,选择全局异步结合精英策略的信息素更新方式。为了随时更新参数,粒子的位置每变化一次,便要反馈到蚁群算法中,将粒子当前的位置信息赋值给α-β及ρ。粒子迭代数次,直至不再出现更优解,则当前最优粒子的位置坐标为全局最优解,将其反馈到蚁群算法中后优化完毕,评价函数的最小的值即为最优解。迭代终止条件选为粒子群目前搜索到的q满足最小预定适应阈值。 混合优化算法的步骤如下:
1) 粒子速度和位置参数的初始化。初始化一定数量的二维粒子群粒子,粒子初始速度的每一维均对应一个矢量速度,且均随机产生:
vi={vα-β,vρ}
(7)
粒子的位置由蚁群算法中的两个参数,分别为“混合启发因子”α-β、信息素挥发度ρ表示,两个参数的意义与式(1)中的相同:
xi={α-β,ρ}
(8)
2) 参数值反馈。调用蚁群算法,将当前粒子群的参数反馈给它,并进行迭代循环以得到最优解。在其被调用的过程中采用全局异步结合精英策略的信息素的更新方式改善求解质量。根据配电网故障定位的特点,将蚁群算法的迭代代数(蚁群算法的一次迭代指所有蚂蚁便利所有地点并释放信息素的过程)限制在5以内,提高算法的搜索速度。通过最优解评价粒子所处的位置,根据评价结果更新粒子的位置及速度,位置和速度更新公式如式(9)和式(10),信息素更新方式如式(11)和式(12)所示:
(9)
(10)
(11)
(12)

2 配电网故障区段定位模型
2.1 开关函数
开关函数用来表示各个分段开关与线路区段的关联关系,当根据配电线路上FTU上传的各个分段开关的故障电流信息来确定具体故障线路区段时,所利用的便是这种关联关系。进行区段定位时,每个测控点对应TSP中的一个地点,应用开关函数求解各测控点状态值的过程中从末测控点(包括分布式电源)向系统电源搜索,在这个过程中依次确定各测控点的运行状态值。对于含分布式电源的配电网故障定位时的正方向规定如下:
1) 分布式电源未投切时,系统电源指向用户端的方向为正方向;
2) 存在分布式电源投切时,规定正方向为系统电源指向投切部位。
此两种情况在原理上不相矛盾,对任何故障进行定位时此方向均应不变,保证定位效率。
需要对开关函数进行改进以适应分布式电源投切的影响,所以对文献[5]中的开关函数进行改进如下所示:
(13)
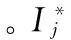
利用改进开关函数的特点,在编程时先对参数k1,k2进行运算,则式(13)化简为式(14),如公式所示,利用函数本身的特性即可在很大程度上减少计算量,提高定位的效率:
(14)
2.2 评价函数
评价函数决定着蚁群粒子群混合算法能否取得最优解和能否将故障区断定位正确。针对故障区段定位的特点,采用文献[1]中的评价函数如下:
(15)
其中,W为开关总数量,B为馈线区段的总数量,xi为区段i的状态值。Ij为开关j处FTU上传的测控点的实际状态信息如式(16)所示:
(16)
将式(13)和式(16)代入式(15),便完成了对评价函数的构建。
应用评价函数,依据各测控点实际状态值和假设故障情况下的状态值对所有路径进行评价,蚂蚁选择评价值最小的路径。由此,便将含分布式电源配电网的区段定位问题转化为求评价函数最小值的问题,根据文献[16]可知,为了减小不可判断故障对定位结果的影响,将次优解作为参考值以提高定位结果的正确率。
3 实验仿真
以图1为例进行仿真分析。如图所示,DG1、DG2、DG3位于分别表示三个分布式电源,其是否投切由K1、K2、K3这三个分布式电源接入网络的开关的状态值表示,数值为1表示对应分布式电源接入配电网,数值为0时情况相反,S为系统电源。用黑色实心圆点表示断路器和分段开关(不进行区分),编号为1~30。两实心圆点之间的线段表示馈线区段,编号为(1)~(30)。
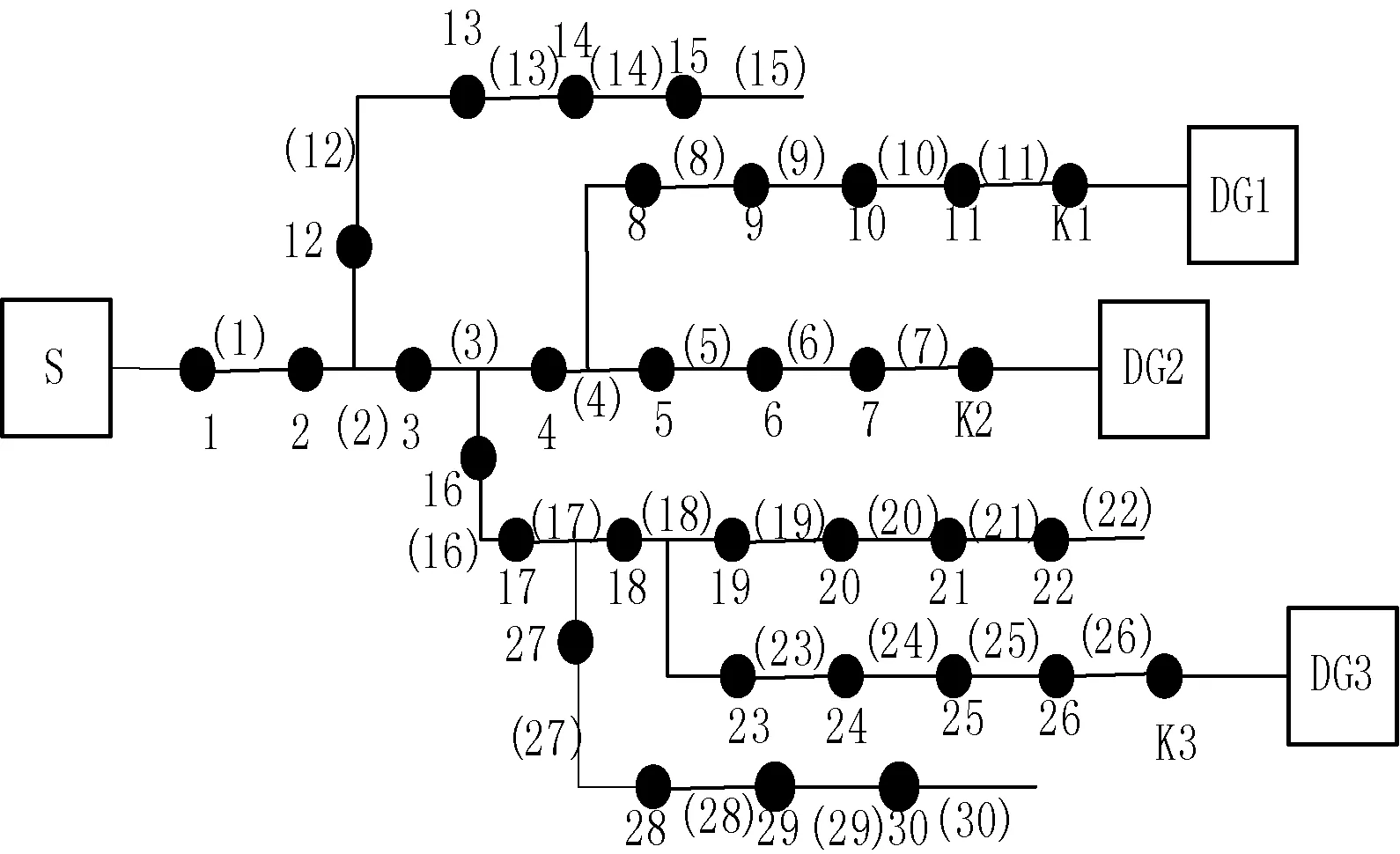
图1 仿真实验配电网图
为了检测基于蚁群粒子群混合优化算法在分布式发电配电网故障定位方面的性能,使用Matlab软件对改进算法仿真。算法的初始参数如下: 蚁群数量m=6,群迭代次数为35次;粒子群最大迭代次数为100,规模为40,加速因子c1=c2=2,惯性权重ω=0.5。
由表1得知,蚁群粒子群混合优化算法进行配电网故障定位输出的结果与实际情况一致,表明该算法对单点故障和复杂故障均能准确定位。当上传的信息出现畸变时,定位结果依然正确并且能够得到对应的畸变位置,这表明其定位准确、容错能力强,可以对导致出现畸变信息的FTU进行定位,以便于对FTU进行修理或替换,从源头上消除引发畸变的原因。

表1 仿真实验结果
为了验证所提出蚁群粒子群混合算法的优越性,选取表1中的2、4、6三种故障情况,针对同一种故障情况分别利用三种蚁群粒子群优化算法与文中改进算法的作对比。算法1为文献[9]中的算法,算法2为文献[14]中的一种方法(蚁群被调用一次进迭代X步,固定ρ,采用粒子群算法优化α、β,调用一次蚁群算法对粒子所处位置的优劣判断一次,调用结束后,信息素重新初始化)。算法3为文献[15]中的一种算法(采用粒子群算法优化α、β、ρ,调用一次蚁群算法对粒子所处位置的优劣判断一次,调用结束后,信息素重新初始化)。为了减小改进算法求解的随机性,重复试验60次,算法比较结果如表2所示。
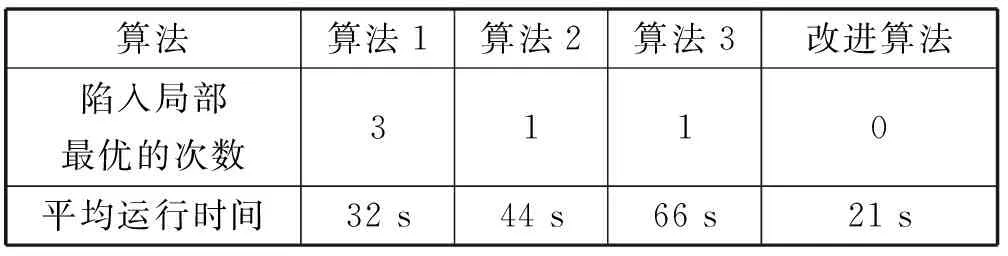
表2 不同算法实验结果比较
分析表2可见,改进算法陷入局部最优的次数远低于前三种方法,且运行时间约在前三种方法的30%~80%之间。由此得出,改进算法在成功降低了人工智能算法容易陷入“早熟收敛”概率的前提下,可以实现对含有分布式电源的配电网的快速准确故障定位。
4 结 语
目前,将蚁群算法应用于分布式发电配电网故障定位时,分布式电源的投切和算法自身缺点使其变得不再适用,为此,提出了一种新方法:
1) 针对分布式电源投切引发的问题对故障定位模型进行了一定改进,利用改进的开关函数能够减少运算量,提高效率。利用改进评价函数进行对含分布式电源的配电网进行定位时,仿真结果显示定位结果准确,可以动态适应分布式电源的投切,且只需要设定一次正方向。
2) 针对蚁群算法收敛效率较低和容易陷入局部最优的缺点,采用混合启发因子“α-β”降低了粒子群算法参数的维数,减少工作量。选择全局异步与精英策略相结合的信息素更新方式与其匹配,保障蚁群算法最终搜寻出最优参数,经验证,两者配合效果良好。
[1] 张颖,周韧,钟凯.改进蚁群算法在复杂配电网故障区段定位中的应用[J].电网技术,2011,35(1):224-228.
[2] 秦立军,杨万涛.蚁群算法在配电网故障定位中的应用及其优化[J].电气应用,2015,34(22):73-76.
[3] 王进强,陈少华.基于改进遗传算法的含分布式电源的配电网故障定位[J].电力科学与工程,2013,2(12):13-17.
[4] 严太山,崔杜武,陶永芹.基于改进遗传算法的配电网故障定位[J].高电压技术,2009,35(2):255-259.
[5] 杨继革.基于遗传算法的配电网故障定位的研究[D].杭州:浙江大学,2004.
[6] 刘蓓,汪沨,陈春,等.和声算法在含DG配电网故障定位中的应用[J].电工技术学报,2013,28(5):280-286.
[7] 高云龙,周羽生,彭湃,等.优化和声算法在含DG配电网故障定位中的应用[J].电力系统保护与控制,2014,42(19):26-31.
[8] 张超,李擎,陈鹏,等.一种基于粒子群参数优化的改进蚁群算法及其应用[J].北京科技大学学报,2013,35(7):955-960.
[9] 李擎,张超,陈鹏,等.一种基于粒子群参数优化的改进蚁群算法[J].控制与决策,2013,28(6):873-878.
[10] 刘健,张小庆,同向前,等.含分布式电源配电网故障定位[J].电力系统自动化,2013,37(2):36-34.
[11] 袁超,曾祥君,邓丰,等.应用边界保护原理提高分布式发电系统并网协调性的方法[J].电网技术,2009,33(5):62-68.
[12] 康龙云,郭红霞,吴捷,等.分布式电源及其接入电力系统时若干研究课题综述[J].电网技术,2010,34(11):43-47.
[13] 王进强.含分布式电源的配电网故障定位的应用研究[D].广州:广东工业大学,2011.
[14] 闵克学,葛宏伟,张毅,等.基于蚁群和粒子群优化的混合算法求解TSP问题[J].吉林大学学报(信息科学版),2006,24(4):402-405.
[15] 夏辉,王华,陈熙.一种基于微粒群思想的蚁群参数自适应优化算法[J].山东大学学报(工学版),2010,40(3):26-30.
[16] 易礼宏.基于蚁群算法的配电网故障定位研究[D].南宁:广西大学,2008.
NEWAPPROACHOFFAULTSECTIONLOCATIONINPOWERDISTRIBUTIONNETWORKWITHDISTRIBUTEDGENERATION
Guo Yuwen
(FacultyofElectricalandControlEngineering,LiaoningTechnicalUniversity,Huludao125105,Liaoning,China)
Aiming at the problem that the traditional fault section locating method is no longer applicable to the distributed generation, a new switch function is proposed to dynamically adapt the switching of multiple distributed powers. The characteristics of the switching function can be simplified and improve its positioning efficiency. Meanwhile, a hybrid optimization algorithm was introduced to solve the problem about premature convergence of ant colony algorithm. In addition, a fault location method based on hybrid optimization algorithm was put forward for fault-section location of the power distribution network containing distributed power. The particle swarm optimization algorithm was used to optimize the parameters of the ant colony algorithm. Also, the method of pheromone update with the combination of global asynchronous and elitist strategy and the method of reducing particle dimension were adopted to reduce the probability of local optima. Consequently, the convergence speed and the accuracy of localization results were improved. A typical example was used to simulate the power distribution network with distributed generation. The results show that the algorithm is capable of accurate positioning not only a single fault but also multiple faults with less time consuming as well as higher fault tolerance.
Distributed power Power distribution network Hybrid optimization algorithm Switching function
TP29
A
10.3969/j.issn.1000-386x.2017.09.004
2017-01-23。辽宁省重点实验室项目(LJZS003)。郭玉雯,硕士生,主研领域:电气工程。

