机载LiDAR点云数据自动生成DEM的方法与精度评价
赵桂华,邹晓亮,郭 丽
(1.西安测绘总站,陕西 西安 710054)
机载LiDAR点云数据自动生成DEM的方法与精度评价
赵桂华1,邹晓亮1,郭 丽1
(1.西安测绘总站,陕西 西安 710054)
设计了一种点云数据快速处理自动生成DEM的算法,介绍了滤波结果的评价方法以及通过标准DEM评价内插的DEM整体精度的方法;并选用河北承德地区的机载激光LiDAR点云数据进行了实验。结果表明,数据处理结果具有较高的精度,为激光点云数据自动生成DEM提供了一种有效的技术途径。
LiDAR点云;DEM;滤波;DEM内插;滤波结果评价;精度评价

地球表面高低起伏呈现为一种连续变化, DEM[1]是定量描述地球表面地貌结构及空间变化的基础数据,蕴含着大量丰富的地貌特征信息。从摄影测量技术的实现途径来看,比较成熟的生成DEM 的方法包括:基于解析测图仪的立体影像数字化扫描方法和基于全数字摄影测量立体环境下的人工采集方法。这两 种方法生成的DEM,点位准确﹑内插精度高,能达到测绘产品需求的高精度要求,但成图周期长,不利于大范围﹑大面积的DEM 成果生产。近年来,出现了基于影像自动匹配生成数字表面模型(DSM)[1],再通过滤波生成DEM的方法,如像素工厂[2-3]和全数字摄影测量系统,但这些设备硬件成本较高。随着机载 LiDAR[4-5]技术的发展,大区域﹑大批量高效获取激光点云数据成为可能,激光LiDAR技术成为了一种新的技术途径。针对机载LiDAR点云数据,本文设计了一种从点云到DEM的数据快速处理算法,通过对点云数据进行滤波﹑内插自动生成DEM,再利用标准DEM数据对其进行整体精度评价,最后通过工程数据验证了算法的可行性。
1 点云数据自动生成DEM算法的设计思路
机载LiDAR点云数据自动生成DEM算法的设计思想为:首先对LiDAR数据进行预处理剔除粗差点,再利用滤波算法对点云数据进行分类,获取地面点和非地面点。本文选用TIN滤波﹑曲面滤波和坡度滤波3种方法对点云进行滤波分类,并对滤波结果进行评价。在计算第I类误差和第II类误差的基础上,选择滤波效果好的地面点数据进行内插计算,自动生成DEM。内插方法实现了反距离加权插值﹑趋势面插值和Kriging插值的DEM自动生成,并将内插DEM与标准DEM进行了精度比对。该流程与常规DEM的成果采集相比,具有快速﹑高效的特点,如图1所示。
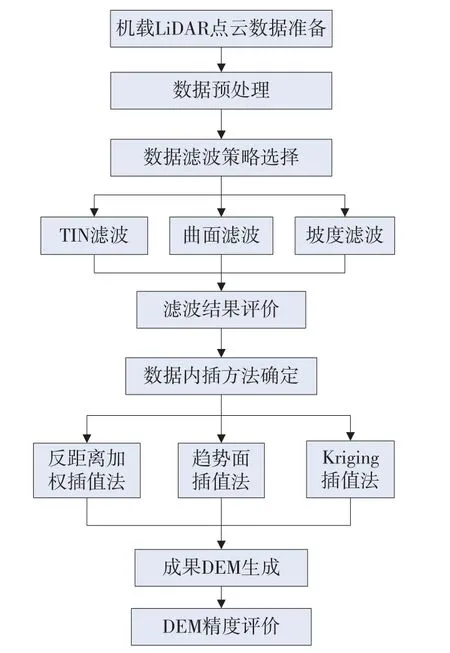
图1 机载LiDAR点云数据自动生成DEM算法流程图
2 点云数据处理算法
2.1 点云数据预处理
激光LiDAR测量是一种无差别的测量方式,具有一定的盲目性和随机性;对在其覆盖区域内的所有目标(飞鸟﹑行人等)均进行测量,并盲目地记录所有回波信号[5],所以LiDAR系统获取的点云数据存在一定量的粗差信息。数据预处理主要完成粗差剔除和地面种子点的选择。粗差点通常与其邻域数据点具有较大高差,一般可采用单一阈值法进行滤波处理,如选取地面高程的最大值作为粗差点剔除的阈值。为了精细化处理,可通过建立多级虚拟格网,结合种子点的选取,设定阈值和搜索窗口的半径,对点云数据进行滤波。种子点的选择是关键因素,因为初始地面种子点的选取直接影响数据点是地面点还是非地面点的判断依据。结合多级虚拟格网技术,引入多尺度格网,筛选初始的地面种子点,为后续点云数据的滤波提供技术支撑。
2.2 点云数据滤波算法
点云数据滤波算法主要指基于相关信息建立若干判别规则,依据这些规则从点云数据中剔除非地面点,获取地面点的过程。本文选择了TIN滤波﹑曲面滤波和坡度滤波3种方法对点云数据进行滤波处理,并对滤波结果进行分析评价,选出滤波效果好的点云数据作为后续内插的原始数据。
1)TIN滤波。其算法原理为:先获取一定的地面种子点组成初始的稀疏TIN;然后对各点进行判断,若该点到三角面的垂直距离及角度小于设定的阈值,则将该点加入地面点集合,实现TIN的不断加密,并重新计算TIN;再对非地面点集合内的点进行判断;如此迭代,直到不再增加新的地面点或满足给定条件为止。
从滤波原理上来看,每增加一个地面点,就要更新一次TIN;随着地面点数量的增加,构建TIN 的计算量也迅速增加。为解决这一问题,本文采用虚拟格网邻域搜索,对该算法进行改进:在获得初始地面点的基础上,对于非地面点集合中的某一点,搜索其周边的10~20个地面点,构建局部TIN,并依据阈值对该数据点进行判断,满足条件就加入地面点集合,否则加入非地面点集合,直至完成所有非地面点的判断;再基于新的地面点集合用相同的方法对新的非地面点集合再做一次筛选判断,从而得到较准确的地面点集合和非地面点集合。
2)曲面滤波。其算法原理为:把地面看作是连续且平缓变化的表面,用带有限制条件的参数曲面进行滤波约束。首先对离散的激光点云数据进行二维排序;再选取种子点区域,设定阈值,利用平面或曲面进行滤波;最后根据滤波结果不断更新趋势面,逐步完成整个测区的滤波过程。
3)坡度滤波。其算法原理为:地表的坡度变化比地物的坡度变化小,对于一个真实的地面点来说,与非地面点之间会有较大的坡度值。坡度阈值的设定是该算法的关键。本文结合多尺度虚拟格网技术和坡度的方向性,以一级格网为单元设定坡度阈值,待判断点比地面点高的称为上坡,比地面点低的称为下坡。对于上坡的情况,由一级格网内的一级地面点与高程值最大的二级地面种子点之间的坡度值来确定;对于下坡的情况,一般取上坡坡度阈值的0.6倍作为下坡的坡度阈值;同时设定最大坡度阈值,防止地形突变引起阈值畸变。
2.3 滤波后点云数据的精度评价
根据国际摄影测量与遥感大会ISPRS小组在对经典滤波算法测评时提出的误差评判标准[6],将点云数据的误分率分为3种:第I类误差﹑第II类误差和总误差。第I类误差是将地面点误分为非地面点的误差,又称拒真误差;第II类误差是将非地面点误分为地面点的误差,又称纳伪误差;第I类误差和第II类误差可以综合得到总误差。第I类误差﹑第II类误差反映了滤波算法的适应性,总误差反映滤波算法的可行性。本文通过对点云滤波误差的分析来评价点云滤波算法的性能。
2.4 滤波后点云数据的内插
DEM内插,即根据若干相邻参考点的高程值求取待定点的高程值。任意一种内插方法都是基于原始地形起伏变化的连续光滑性,或者说邻近的数据点间必须有很大的相关性,才可能由邻近的数据点高程内插得到待定点的高程。本文采用反距离加权插值法﹑趋势面插值法和Kriging插值法实现DEM的内插。
2.4.1 反距离加权插值法
反距离加权插值法[7](IDW)基于相似相近原理,即两个物体距离越近,其性质越相似。以待内插点为中心,在待内插的点X﹑Y 处内插变量Z 值时,在局部邻域中计算各数据点的加权平均值,其公式为:

式中,Zi为估算点的数值;Z0为插值要素在第i 点的实测值;λi为预算过程中要使用的各种采样点的权重;n为参与插值的实测点的数量。确定权重的公式为:
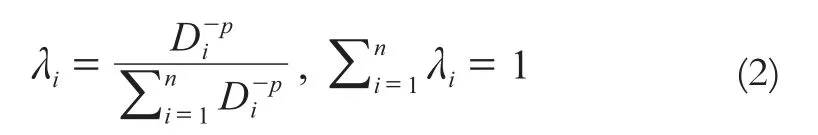
式中,P为幂指数;Di为第i点和各已知样点之间的距离。采样点在预测点值的计算过程中所占的权重受幂指数影响,即随着采样点与预测值之间距离的增加,采样点对预测点影响的权重按指数规律减少。
2.4.2 趋势面插值法
趋势面插值法是利用多项式方程拟合已知点,用于估算其他点的高程值,属于一种非精确的插值方法。该方法通过选择一个二元函数来逼近采样数据的整体变化趋势。二元函数的一般形式为:
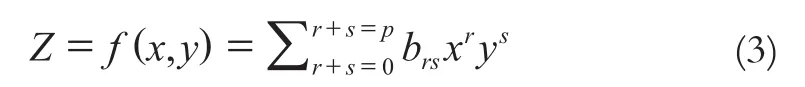
当p=0时,此二元函数表示水平面;当p=1时,此二元函数表示倾斜平面;当p=2时,此二元函数表示趋势面,可用于模拟地形起伏。一次趋势面需要估算3个系数,而3次趋势面需要估算10个系数才能预测未知点的值,因此趋势面模型次数越高,计算量越大。
2.4.3 Kriging插值法
Kriging[8-9]插值法也称空间局部估计或空间局部插值,是地统计学中最经典的方法之一。在二阶平稳﹑本征假设等数学假设条件下,该方法是建立在变异函数理论及结构分析的基础上,在有限区域内对区域化变量的取值进行无偏最优估计的一种方法。本文实现了基于球状模型的Kriging插值算法。球状模型的一般公式为:
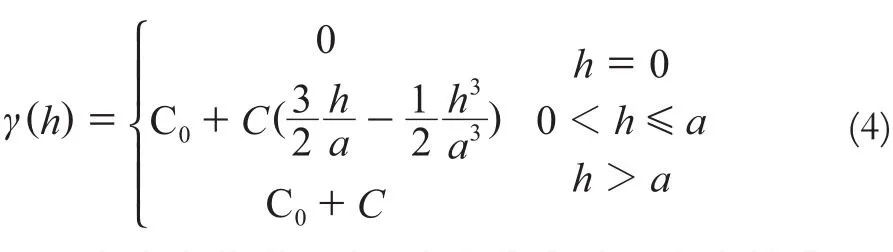
式中,C0为块金常数;C0+C为基台值;C为拱高; a为变程。当C0=0,C=1时,即标准球状模型。
2.5 基于标准DEM的整体精度评价方法
为了对DEM 内插成果进行精度评价,本文提出了基于标准DEM的整体精度评价方法。整体精度评价是将标准DEM与内插的DEM结果进行整体比较,统计整体的误差分布。标准DEM是利用 TerraSolid 软件进行人工精细分类生成的DEM 数据。该评价方法的基本思路是从标准DEM 中随机选取一定数量的点作为评价控制点,与内插的DEM进行比较,同时设定剔除误差的阈值进行统计计算,统计点集的中误差和平均误差。分析滤波内插后点云数据中是否存在粗差点,若存在粗差点,则对其区域进行人工编辑,剔除内插有误的点,再进行数据点集的误差统计和分析。
3 实验结果及精度分析
3.1 实验数据
本文选取的实验数据为河北省承德地区机载激光LiDAR ALS50传感器获取的离散激光点云,见图2,激光点云间隔为1.2 m,选取677 m×686 m的区域,数据点共计28 880个;最小高程值为325.33 m,最大高程值为434.06 m;影像数据的分辨率为0.25 m,见图3。
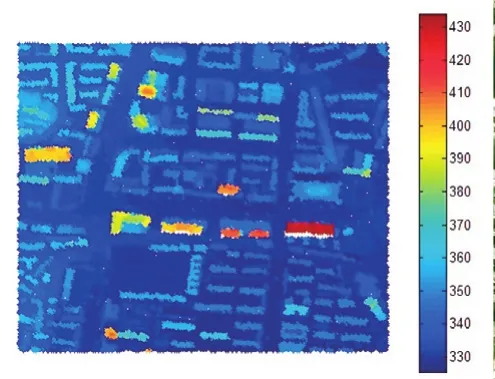
图2 点云数据图

图3 影像数据图
3.2 点云滤波
为了使滤波结果显示得更直观,采用滤波后的点云数据与对应影像数据叠加的方式来显示滤波后的点云数据。利用TIN滤波﹑曲面滤波和坡度滤波3种方法滤波后所得到的地面点与对应影像的叠加情况,如图 4~6所示。

图4 TIN滤波
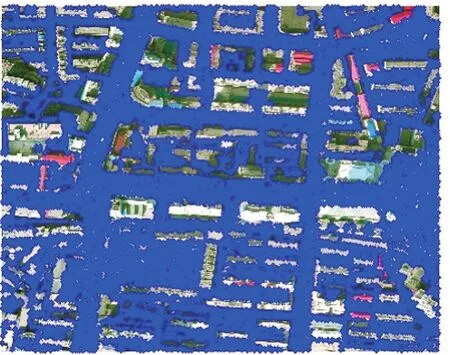
图5 坡度滤波

图6 曲面滤波
3.3 滤波结果评价
滤波的目的是为了最大限度地恢复真实地形,滤波后得到的地面点一般要求包含尽可能少的非地面点,即要尽可能地减小第II类误差的发生。实验中主要考虑第II类误差的影响,并综合考虑总误差的影响。表 1反映了利用3种滤波算法对实验数据滤波后的第I类误差﹑第II类误差和总误差分布情况。
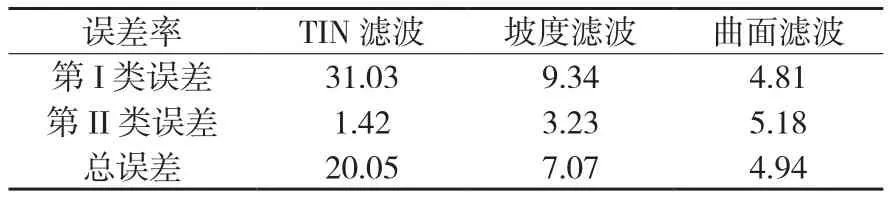
表1 不同滤波方法的误差率/%
由表1可知,TIN滤波的第II类误差率为1.42%,效果最好,但是总误差率为20.05%;坡度滤波和一次曲面滤波的第II类误差控制得较好,但坡度滤波的总误差大于一次曲面滤波的总误差;同时采用目视判读的方法,将滤波后的点云数据与影像数据叠加进行判断,目视结果也是一次曲面滤波优于坡度滤波。
3.4 滤波后点云内插
根据滤波结果的误差率分析,本次实验内插前的点云数据选取曲面滤波算法所获得的数据,如图7所示。分别采用IDW插值﹑趋势面插值和Kriging插值3种算法对内插前的地面点数据进行处理,其内插后的结果如图8~10所示,形成内插DEM。

图7 内插前的点云数据
3.5 整体精度评价
将滤波内插的DEM成果数据与标准DEM成果数据进行逐点比较,计算中误差和平均误差。在剔除大于7 m粗差点的基础上,IDW内插的中误差为0.61 m,平均误差为0.30 m;趋势面内插的中误差为0.99 m,平均误差为0.51 m;Kriging内插的中误差为0.55 m,平均误差为0.28 m。从整体评价的结果来看,IDW插值和Kriging插值方法的中误差和平均误差的趋势较一致,而趋势面插值法的误差值相对较大。基于Kriging插值的总体评价如图11所示。总的来说,相较于3种方法,Kriging内插得到的DEM结果最优。最终自动生成的DEM成果选取Kriging内插的DEM结果。

图8 IDW内插

图9 Kriging内插
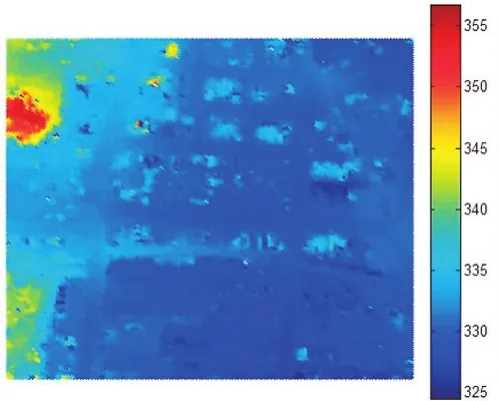
图10 趋势面内插

图11 Kriging内插总体评价
4 结 语
本文设计了机载 LiDAR点云数据快速处理生成DEM的流程,提出了通过标准DEM评价基于LiDAR点云滤波内插生成的DEM整体精度的方法,并利用机载LiDAR点云工程数据进行了实验验证。结果表明,Kriging插值算法在快速自动生成DEM方面精度高,处理流程总体设计合理,整体精度评价方法具有可操作性。该方法是行之有效的。
[1] 全晓萍,宋志勇.基于DEM 数据的地形分析研究与实现[J].科技信息,2007(28):345-349
[2] 曹敏,史照良.新一代海量影像自动处理系统“像素工厂”初探[J].测绘通报,2006(10):55-58
[3] 邹晓亮,缪剑,张永生,等.基于像素工厂的无人机影像空三优化技术[J]测绘科学技术学报,2012,29(5):362-367
[4] 余洁,张国宁,秦昆,等. LiDAR数据的过滤方法探讨[J].地理空间信息,2006,4(4):8-10
[5] 赖旭东.机载激光雷达基础原理与应用[M].北京:电子工业出版社,2010:37-99
[6] Sithole G, Vosselman G. Experimental Comparison of Filter Algorithms for Bare-earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry & Remote Sensing,2004,59(1/2):85-101
[7] LIU X Y, GUO Q H, SU Y J, et al. Airborne LiDAR for DEM Generation: Some Critical Issues[J].Progress in Physical Geography,2008,32(1):31-49
[8] Vieira S R,Hatfield J I, Nielsen D R, et al. Geostatistical Theory and Application to Variability of Some Agronomical Properties[J]. Hilgardia,1983, doi:10.3733/hilg.v51n03p075
[9] 王政权.地统计学及在生态学中的应用[M].北京:科学出版社,1999:102-132
P23
B
1672-4623(2017)09-0009-04
10.3969/j.issn.1672-4623.2017.09.003
2016-07-15。
项目来源:西安科技创新工作站资助项目(2014-CX0452)。
赵桂华,硕士研究生,工程师,研究方向为激光LiDAR数据处理、数字摄影测量、影像分析与解译。

